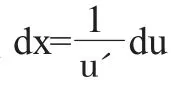對第一類換元積分法的研究與改進
陳 思 閆偉杰
(浙江同濟科技職業學院,浙江 杭州311231)
1 概述
第一類換元積分法(也稱湊微分法)是在高等數學學習過程中遇到的第一種積分方法,也是在積分計算題目中運用最廣泛的一種方法。其思路是通過引進中間變量作變量替換,使原式結構變得更加簡單,從而解決較為復雜的不定積分問題。常規的換元方法存在選取合適的中間變量難、湊微分時容易配錯常數等問題,尤其是對于數學基礎薄弱、微分公式運用不夠靈活的學生,在做題過程中特別容易出錯,從而產生畏難情緒。針對這個問題,本文提出了一種更為簡單且不容易出錯的換元方法,避開了湊微分時配常數的計算,降低了換元難度。
2 第一類換元積分的常規解法
第一類換元積分法是復合函數鏈式法則的逆推。若F(x)是f(x)的一個原函數:
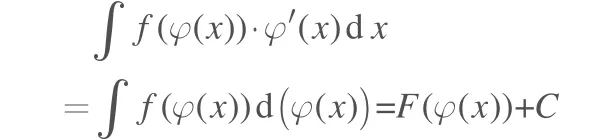
其中被積函數是以f(φ(x))·φ'(x)出現的,但解決實際題目時,很少會直接給出這樣的結構,所以選取一個合適的中間變量u=φ(x),是解決題目的關鍵。
常規解題思路為:
(1)觀察:選取合適的中間變量u=φ(x);
(2)求微分:φ'(x)dx=d(φ(x));
(3)換元:將原式中的φ'(x)dx 換為d(φ(x)),或是原式中的c·φ'(x)dx 換為c·d(φ(x)),其中c 為常數;
(4)求積分:將簡化過的式子運用合適的積分公式,求出原函數。
下面以兩道例題來說明:
(1)觀察:選取u=1+x3;
(2)求微分:3x2dx=d(1+x3);
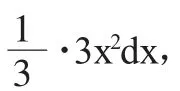
(4)求積分:

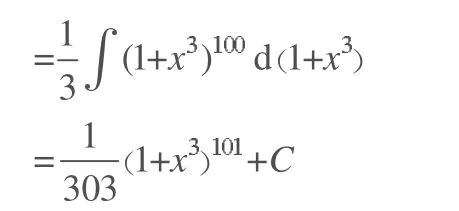
(1)觀察:選取u=3lnx+1;
(4)求積分:
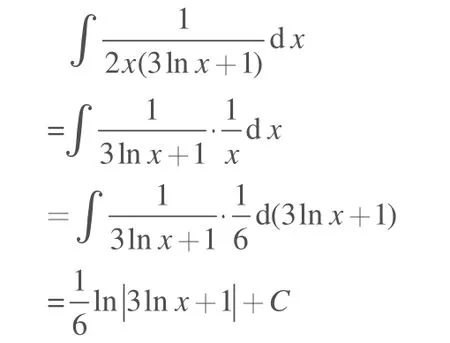
從上面兩道例題中,不難發現解題過程中存在兩個難點:
第一,換元時,若題目中包含c·φ'(x)dx,需要進行常數的計算。學生經常在此處漏算或錯算常數,考試中這常常是該類題目的主要失分點;
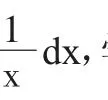
3 改進的換元方法——直接對被積變量進行換元求解
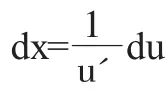
步驟如下:
(1)觀察:選取合適的中間變量u=φ(x);
(3)求積分:將簡化過的式子運用合適的積分公式,求出原函數。
前面兩個例子用直接對被積變量進行換元求解如下:
(1)觀察:選取u=3lnx+1;
(2)計算微分公式并直接換元

(1)觀察:選取u=3lnx+1;
(3)求積分:

4 結論