雙頻激光相干探測差頻信號影響因素分析

任建迎,孫華燕,趙延仲,張來線

(1.航天工程大學研究生院,北京 101416；2.航天工程大學電子與光學工程系,北京 101416)

1 引 言

激光相干探測可實現對目標速度的精確測量,與直接探測相比具有測量精度高、靈敏度好、抗干擾能力強等諸多優點,研究人員針對激光相干探測技術開展了大量的研究工作[1-4]。但是在高速運動目標探測領域,由于目標的運動速度快,多普勒頻移量大,受探測器帶寬和數據采集系統的限制,現有的激光相干探測方法無法實現對高速運動目標的探測。

雙頻激光相干探測技術利用差頻光實現高速運動目標的低多普勒頻移量探測,大大降低了對系統設備參數的要求[5-7]。課題組提出了高速運動目標雙頻激光相干探測方法,采用單頻光源分光技術實現雙頻激光的差頻,利用差頻光對高速運動目標進行探測,因為差頻光的頻率遠低于光頻,從而克服了低探測帶寬和大多普勒頻移的矛盾。作為探測信號的差頻光直接影響系統探測的性能,因此分析差頻光性能的影響因素對雙頻激光相干探測技術的應用至關重要。激光器是影響差頻光性能的關鍵,對于平穩準單色光源,其頻譜在頻域內具有一定的頻帶寬度,即激光器線寬,在時間域內表現為有限長的相干長度或相干時間。激光線寬是衡量激光器性能的重要指標,根據經典干涉理論可知,相干場的條紋對比度、差頻光的線寬與激光線寬有直接關系。李成強等研究了激光線寬對外差激光探測性能的影響,結果表明線寬的增加時影響中頻信號提取精度[8]；陳明惠等研究了掃頻激光瞬時線寬的影響因素,掃頻激光的瞬時線寬隨著色散的增加而變寬[9]；安穎等研究了超短時延的DFB激光器的動態線寬,提出了一種利用局部均值分解(LMD)的時頻分析法測量激光動態線寬的方法[10]；陳長水等研究了差頻法產生中紅外光源的方法,結果表明輸出光源線寬與抽運光和信號的線寬有關[11]。以上研究充分說明光源線寬對相干探測的重要影響,但對于雙頻激光相干探測的差頻光影響沒有具體分析,因此通過理論分析線寬對差頻光的性能影響,對雙頻激光相干探測技術的應用具有重要意義。

本文根據雙頻激光相干探測高速運動目標的原理,結合隨機過程理論分析了差頻光的影響因素。通過維納-辛欽定理得到了差頻光的功率譜公式,根據此公式分析了激光線寬、振幅比對差頻信號功率譜、信噪比的影響。討論了差頻光的條紋對比度與線寬和光程差的關系。

2 雙頻激光相干探測技術理論

雙頻激光相干探測技術通過雙頻激光相干產生的差頻光探測運動目標,經目標反射后的回波光與參考差頻光混頻,得到低多普勒頻移信號,經過濾波降噪處理提取目標的速度和距離信息。雙頻激光相干探測技術中差頻光的產生方法主要包括:一是注入式鎖模激光器的光學混頻法[12-13]；二是單頻光分束后將其中一路移頻,然后將兩束光合束混頻[14]。

在雙頻激光相干探測中,拍頻光的頻率噪聲和相位噪聲與激光器輸出信號的線寬、強度穩定性有直接關系。基于單光源分束移頻法的雙頻激光相干探測系統如圖1所示,激光器發射光源經過分束鏡等比例分束,分束后的光場強度時域特性可表示為:

圖1 雙頻激光相干探測原理框圖Fig.1 Principle block diagram of dual frequency laser coherent detection

E1=E0(1+a(t))cos[2πft+φ1(t)]

(1)

其中,E0表示光場振幅;φ1(t)表示光場的隨機相位;a(t)表示光源強度的隨機波動,反應的是激光器強度噪聲的大小,本文主要分析光源線寬對雙頻相干光的影響,因此忽略強度噪聲的影響。另一光束經過移頻器移頻后的時域光場可表示為:

E2=ηE0cos[2π(f1+fIF)t+φ2(t)]

(2)

其中,η表示移頻器的衍射效率,此處是影響差頻信號振幅比的主要因素;φ2(t)表示移頻后的光場隨機相位;fIF表示移頻量。移頻后的光束與另一路光束通過耦合器混頻,產生的差頻光場強度的時域特性可表示為:

(3)

差頻光經運動目標反射后的時域光場可表示為:

Es=αAcos[2π(fIF+δ)t+φs(t)]

(4)

其中,α表示回波光信號與參考光信號振幅比,0<α<1,δ=2VfIF/c表示目標運動引起的差頻信號多普勒頻移。由式(4)可知,探測高速運動的差頻信號頻率為fIF,頻移量fIF一般在百兆赫茲到吉赫茲量級,屬于微波波段。以1550 nm波長激光器為例,當頻移量fIF=1GHz,目標運動速度為V=340 m/s時,雙頻激光相干探測技術多普勒頻移為2.2667 kHz,而傳統單頻激光相干探測的多普勒頻移為438.71 MHz,相比傳統單頻激光相干探測技術,雙頻激光相干探測技術多普勒頻移量低了5個數量級,大大減小了對探測器、采集設備、數據處理設備性能的要求,可實現更高速度目標的探測。

3 差頻信號功率譜分析

當激光光源服從廣義平穩隨機過程時,根據維納-辛欽定理,可以通過差頻信號自相關函數的傅里葉變換得到信號功率譜密度函數,差頻信號的自相關函數可表示為:

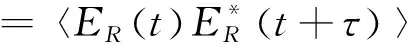
=A2cos(2πfIFτ)×Re〈exp[-jΔφ(t,τ)]〉

(5)

其中,Re表示取函數的實部；〈〉表示求函數均值,Δφ(t)=φR(t+τ)-φR(t)表示不同時刻差頻光相位的相關性,其服從零均值隨機高斯分布。由上式可知,Re〈exp[-jΔφ(t,τ)]〉項是決定差頻光線寬的關鍵量,即激光器的相位噪聲是影響線寬的關鍵因素。根據理論關系式[15-16]:

〈eiΔφ(t,τ)〉=e-〈Δφ2(τ)〉/2

(6)

其中,〈Δφ2(τ)〉=2πΔf|τ|表示差頻光隨機相位的方差；Δf表示激光器的輸出信號的半高全寬(full width at half maximum,FWHM),當時延τ非常小時,兩光束是完全相干的[10],τc=1/πΔf表示激光光源的相干時間。則差頻光場的自相關函數可表示為:

G(τ)=A2cos(2πfIFτ)e-πΔfτ

(7)

上式的傅里葉變換為差頻光場的功率譜,體現的是差頻光強的頻域特性。差頻信號功率譜函數可表示為:

(8)

由上式可知中心頻率是fIF,功率譜分布受激光線寬Δf和振幅比的影響,差頻信號功率譜函數表現為洛倫茲線型。移頻量一定,且衍射效率固定的條件下不同激光線寬的差頻信號功率譜分布如圖2所示,由圖可以看出隨著光源線寬的增加,差頻信號功率譜隨之展寬,功率譜幅度下降。當移頻量一定,且光源線寬固定時,不同衍射效率條件下的差頻信號功率譜分布如圖 3所示,衍射效率影響著兩差頻信號的振幅比,由圖可得,當衍射效率越大功率譜幅度越大,此時的信號幅度越強。

差頻信號信噪比計算可以采用頻域積分的方法,認為功率譜峰值外的其他部分為噪聲。信噪比計算公式:

(9)

差頻信號的信噪比隨光源線寬變化曲線如圖 4所示,由圖可得,隨著光源線寬的增大信噪比隨之下降。受移頻器自身噪聲、環境、衍射效率等多種因素的影響,頻移量并不是一個嚴格固定的量,而是一個隨時間起伏的變化量，移頻擾動對功率譜的影響如圖5所示。移頻器的頻率擾動量可以通過移頻穩定度來衡量[17],移頻穩定度可表示為:

(10)

其中,fn表示移頻器的擾動頻率；Δf表示移頻器的中心頻率。

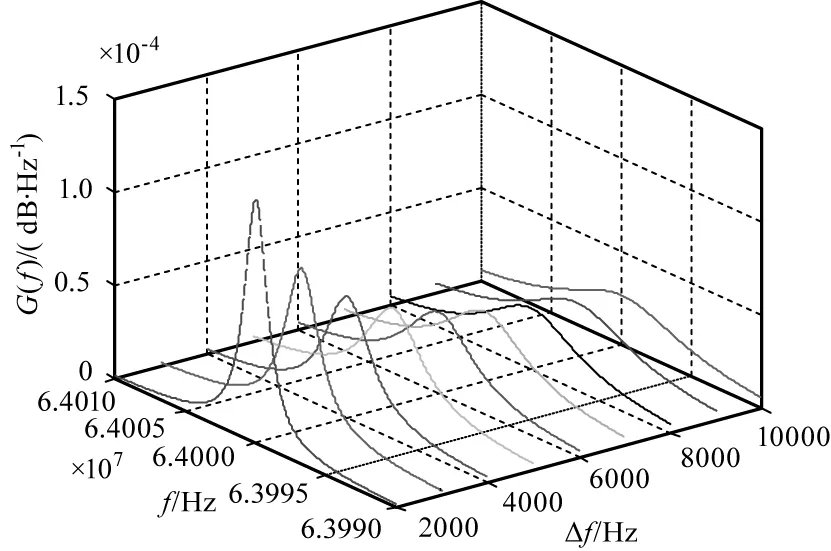
圖2 不同線寬的差頻信號功率譜Fig.2 Power spectrum of different linewidth

圖3 不同振幅比的差頻信號功率譜分布Fig.3 Power spectrum distribution with different amplitude ratio

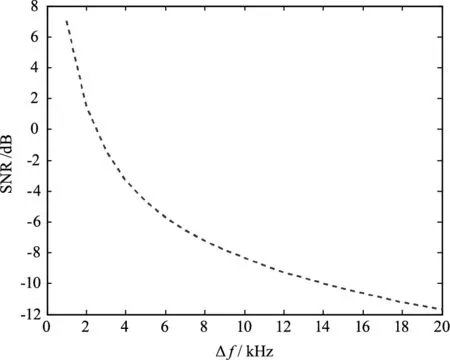
圖4 差頻信噪比隨光源線寬變化曲線Fig.4 SNR curve with the linewidth of the light source

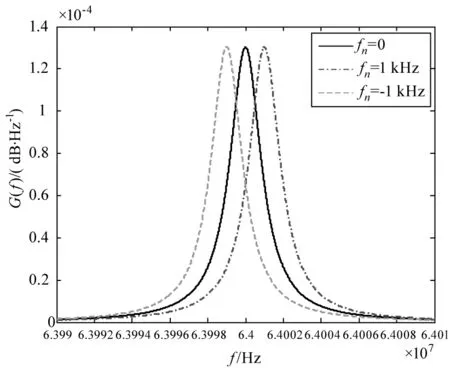
圖5 移頻擾動對差頻光的影響Fig.5 The effect of frequency shift disturbance on differential frequency light

差頻光的條紋對比度是衡量相干性能的重要參數,根據兩光束在P點的合振動光強度分布為:

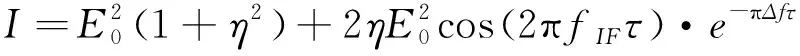
(11)

根據相干場某點的干涉條紋對比度定義[18],條紋條紋對比度可表示為:

(12)

Imax表示相干光場的最大值,當2πfIFτ=2nπ(n=0,1,2,…),差頻光場強度取最大值:

(13)

Imin表示相干光場的最小值,當2πfIFτ=(2n+1)π(n=0,1,2,…)時,差頻光場強度最小值:

(14)

差頻光的條紋對比度可表示為:

(15)

(16)

式中,n是與延遲時間τ成正比的正整數,延遲時間越大n值越大,延遲時間是由兩路光的光程差引起的。不同線寬的條紋對比度變化曲線如圖 6所示,由圖6可知隨n的增加,差頻光條紋對比度下降,且光源線寬越大下降速度越快,即光源線寬越大受光程差的影響越大。因此在雙頻激光相干探測中盡量保持合束前兩路光的光程相等。不同衍射效率下的條紋對比度變化曲線如圖 7所示,由圖可以看出,在短延時下的條紋對比度主要受振幅比的影響,因此在生成差頻信號中,盡可能的保證兩路光的振幅比相等。

圖6 不同線寬的條紋對比度變化曲線Fig.6 Variation curve of fringe contrast with different line widths

圖7 不同振幅比下的差頻光條紋對比度Fig.7 Contrast of light fringe with different amplitude ratio

4 差頻光信號實驗測試

實驗過程中,采用532 nm單縱模激光器,最大輸出功率200 mW,線寬<10-4nm,振幅穩定度<0.5 %,功率穩定性<1 %,相干長度>50 m。分束器的分束比為1:1；移頻器采用Gooch&Housego AOMO 3080-125移頻器,最大移頻量80 MHz,衍射效率0.95,探測器距離合束鏡頭10 cm,避開的傳輸信道對差頻光的影響。

探測器響應的差頻光信號如圖8所示,差頻光的頻率和幅度受到干擾,這是由于激光器、移頻器不穩定造成的頻率擾動和幅度起伏。差頻光的頻譜分布如圖9所示,圖9(a)和9(b)為不同時刻差頻光的頻譜,圖9(a)的中心頻率為69.13 MHz,3 dB線寬為760 kHz,圖9(b)的中心頻率為69 MHz,3 dB線寬為740 kHz。以上不同時刻差頻光的中心頻率的變化,證明了移頻器存在移頻量的擾動。差頻光線寬的變化主要是由激光器瞬時線寬的變化引起的。

根據實驗測試結果可知,由于激光器和移頻器噪聲的存在,差頻光并不是嚴格的穩定信號,受移頻器頻率擾動的影響差頻光的中心頻率存在微小的變化,差頻光的線寬受激光器瞬時變化影響存在起伏,頻率擾動和強度起伏對差頻光的影響在本文中不做描述。

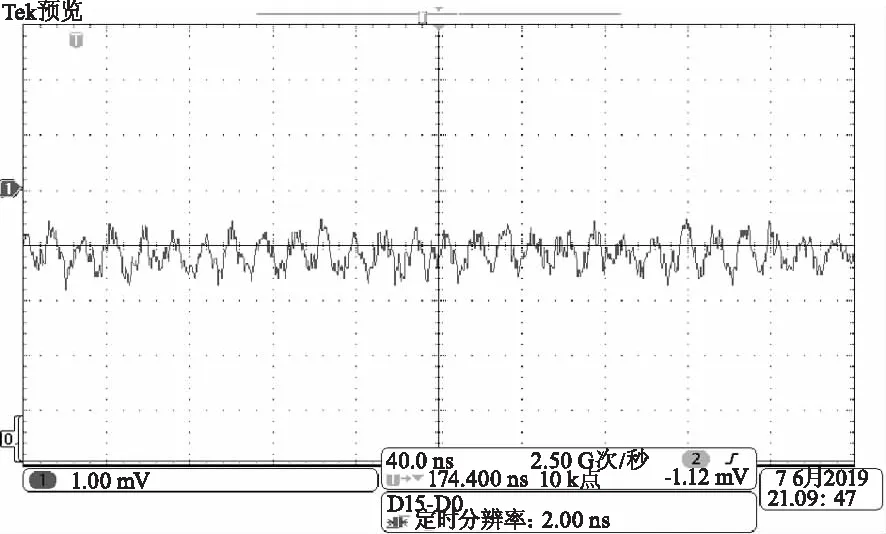
圖8 探測器響應的差頻光信號Fig.8 The difference frequency signal output by the detector

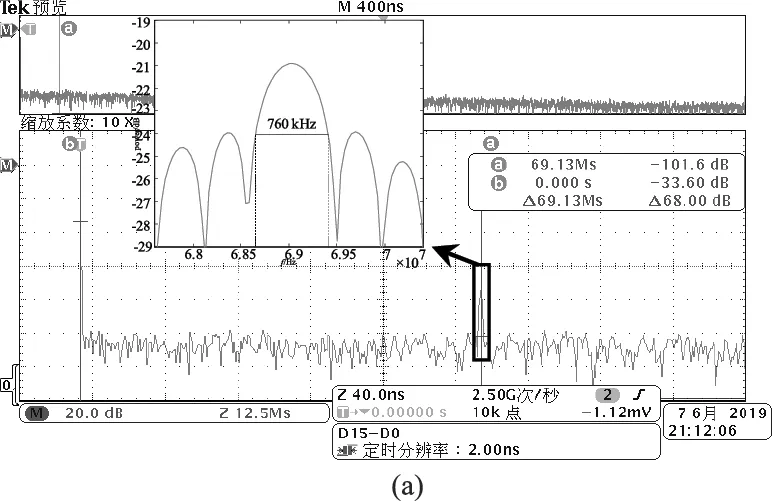
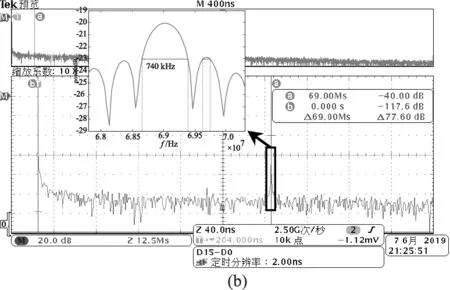
圖9 不同時刻差頻信號頻譜及3dB線寬Fig.9 Different time difference frequency signal spectrum and 3dB line width

5 結 論

針對單頻激光相干探測系統探測高速運動目標時的大多普勒頻移與低探測帶寬的問題,提出了單光源分束移頻的雙頻相干探測方法,簡單分析了雙頻激光相干探測的低多普勒頻移的優勢,介紹了差頻光的產生方法。結合維納辛欽定理得到了差頻光的功率譜函數,重點研究了激光線寬、振幅比、光程差對差頻光功率譜、信噪比、條紋對比度的影響。最后通過實驗驗證了差頻光的產生方法,證明了激光器線寬、移頻器頻率擾動對差頻光線寬和中心頻率的影響。同時實驗結果證明激光器、移頻器等噪聲對差頻光振幅有一定影響,后續還需要深入的研究激光器和移頻器噪聲擾動對差頻光的影響。