基于自適應神經模糊Petri網的電機故障診斷

程學珍，王常安，李繼明，許傳諾

(山東科技大學 電氣與自動化工程學院，山東 青島 266590)

電機系統是由多數量功能模塊組成的系統，其故障往往呈現不確定性以及非線性的特征，任意功能模塊的微小偏差都可能導致整個系統的崩潰[1]。因此為其尋找一種合理、有效的故障診斷方法至關重要。

目前電機的故障診斷方法主要包括定量分析和定性分析兩類。其中定量分析方法包括基于解析模型方法和數據驅動方法。目前常用定量分析的數據驅動方法對電機系統中轉子以及軸承的故障特征信號進行處理。文獻[2]將Prony方法與選帶細化技術相結合，對轉子斷條故障特征頻率附近的小頻段進行局部放大分析，提高了計算的準確性，但是在低噪背景下，其診斷結果難以令人滿意；文獻[3]提出一種改進矩陣束濾波與檢測的轉子故障診斷技術，通過改進的矩陣束算法，有效克服了噪聲的影響，對短時數據具有較好的分辨能力。文獻[4]提出利用Park矢量模變換技術與旋轉不變信號參數估計技術，通過Park矢量模變換技術消除工頻分量的影響，在保證準確性的前提下，減少了計算量。文獻[5]提出一種基于小波變換和希爾伯特變換相結合的電機軸承故障診斷技術，通過希爾伯特變換解調調制信號，實現對故障特征信號的有效分析，同時該方法在小波變換中引入Thselect函數，利用函數的自適應能力，調節不同噪聲情況下的閾值大小，實現消除高頻信號的功能，提高了算法的自適應能力，但是該方法忽略了低頻信號的噪聲干擾，仍然會導致誤判漏判的現象。基于數據的定量分析方式雖然可以根據特征分量進行故障分析，但是在電機系統中，故障檢測的準確性往往會受到干擾信號的影響而降低，因此定量分析法難以滿足電機系統故障診斷需求。

定性分析是依靠系統內部知識建立系統模型的一種方法[6]，主要有圖論方法、專家系統和定性仿真等。其中Petri網是一種圖論方法，可利用目標系統中元件關系來構建有向圖的組合模型，準確地處理離散事件發生的順序、并發和沖突的關系[7]。近年來隨著國內外學者的研究，Petri網在電機系統故障檢測中的應用逐漸增多，并且取得了較好的診斷結果。文獻[8]針對故障傳播過程中的不確定性，定義了故障Petri網的概率變遷方法，解決了以往Petri網故障診斷過程只關注庫所狀態的弊端，但是其概率變遷的方式不具備自適應能力。文獻[9]提出構建修正狀態類圖，充分利用Petri網在實時系統中的重要作用，結合系統各執行機構建立可觀的Petri網。文獻[10-11]運用有色Petri網和建模工具CPNTools建立了有色Petri網模型，提高了故障診斷的效率和模型的直觀性。文獻[12]將Petri網和模糊推理相結合，有效的解決了一部分隨機性、不確定性的故障問題，極大提高了故障診斷過程中定位故障源的能力。文獻[13]對模糊Petri網(fuzzy Petri net，FPN)進行了嚴謹的數學推理，給出了矩陣化的推理過程，對FPN的應用和發展奠定了堅實的理論基礎，但其權值的獲取仍然依靠專家經驗，適應性較差。

為克服以往FPN準確性和自適應能力差的問題，提高算法對電機系統故障診斷的能力，本研究提出了基于神經模糊Petri網(neural fuzzy Petri net，NFPN)的故障診斷方法，其創新性如下：

1) 使用失效模式與影響分析方法對故障數據進行處理，解決了初始參數賦值經驗化的問題。

2) 引入高斯函數代替變遷可信度，通過變遷影響因子反映變遷對其輸出庫所的影響能力。

3) 通過BP神經網絡算法(back propagation neural network，BPNN)對權值和變遷影響因子進行學習訓練，提高算法的自適應能力。

通過仿真驗證本研究所提出的算法能準確地診斷三相異步電動機的故障，具有較好的準確性和適應性，可有效提高電機的檢修和維護效率。

1 神經模糊Petri網

1.1 BP神經網絡

BP神經網絡是具有前向傳播和誤差反傳兩種工作模式的智能算法，其中前向傳播反映了系統的運行過程，誤差反傳反映了對系統準確度的調節過程。通過兩種工作模式，BP神經網絡可以根據輸入輸出值找到系統的相關規則，并依據該規則在實際運行過程中準確推導輸出，具有較好的非線性映射能力，因此被廣泛應用于電機系統的故障診斷。

1.2 NFPN的定義

在電機系統中，故障的發生充滿了不確定性，導致提取的故障信息具有模糊特性。而傳統Petri網并不能處理該類型的數據，文獻[14]將模糊理論引入到Petri網中得到FPN，并將其應用于三相異步電動機的故障診斷。與傳統Petri不同，FPN清晰地反映出系統中各部件的狀態信息量，能夠滿足模糊事件的處理需求。

根據FPN理論和BP神經網絡算法的特性，定義NFPN為一個9元組：

SNFPN=(P,T,I,O,M,W,α,F,B)。

1)P={p1,p2,…,pn}T，表示庫所的集合。

2)T={t1,t2,…,tm}，表示變遷的集合。

3)I為輸入矩陣，描述庫所到變遷的映射。對于輸入矩陣元素δij={0,1}，當pi是tj的輸入時，δij=1；當pi不是tj的輸入時δij=0，其中i=1,2,…,n;j=1,2,…,m。

4)O為輸出矩陣，描述變遷到庫所的映射。對于輸入矩陣元素γij∈{0,1}，當tj是pi的輸入時，γij=1；當tj不是pi的輸入時，γij=0，其中i=1,2,…,n;j=1,2,…,m。

5)M=(m1,m2,…,mn)，表示庫所標識分布向量。

7)α=(α1,α2,…,αn)，αi∈[0,1]，表示庫所pi所代表故障事件的置信度。

8)F={f1,f2,…,fn}，為庫所最小割集故障發生率的集合。

9)B=(b1,b2,…,bm)，表示變遷對其輸出庫所的影響能力，bi為變遷影響因子。

2 NFPN的學習與診斷

為提高FPN的自適應能力，本研究在FPN的基礎上結合BP神經網絡給出了NFPN的定義。同時，結合BP神經網絡算法的自學習能力，對權值和變遷影響因子進行訓練，提高算法的適應性和準確性。

2.1 NFPN故障診斷

在電機系統中，設備自身的物理結構與故障、設備的故障與故障之間都存在著多重映射的關系，故障在傳播過程中存在著冗雜性與多樣性，并伴隨著多種傳播模式。

為體現NFPN算法解決上述復雜故障傳播模式的能力，清晰的展現出NFPN算法的推理過程與并行處理的特點，提高算法的適應性。定義如下3個算子:

2) 取大算子⊕:C=A⊕B，A，B和C均為m×n矩陣，cj=max(aij,bij),i=1,2,…,m；j=1,2,…,n。

3) 直乘算子?:C=A?b，A為m×n矩陣，b為m維向量，則cij=aij·bi，i=1,2,…,m；j=1,2,…,n。

借助上述算子定義，進行演繹推理計算：

1) 置信度推理

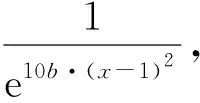
(1)

根據NFPN算法故障推理結果的要求，αk+1=αk時，推理結束，否則繼續由αk推導得到αk+1，α0為系統規定的初始值。

2) 變遷點火判別

定義：X=(x1,x2,…,xm),X為具有標識的庫所置信度與對應權值乘積等效和的m維向量。

Xk=(αk*Mk)·W。

(2)

為判別變遷使能情況，引用Sigmoid函數:

(3)

其中，c為正無窮大，λ為變遷閾值,Sk=(s1,s2,…,sm)為變遷的預使能矩陣，使得當x≥λ時，滿足點火條件s(x)=1；當x<λ時，s(x)=0。

3) 故障傳播推理

NFPN的故障推理過程反映了系統故障的傳播方向，其中托肯反映了系統故障發生的情況，隨著變遷點火，托肯將由輸入庫所傳遞給其輸出庫所。在Petri網中托肯的分布稱為庫所標識，用向量M表示。故障傳播推理公式為：

(4)

其中,Mk+1的變化反映了庫所中托肯的變化，M0為給定的系統初始值。

2.2 NFPN故障預測

NFPN故障診斷是在已知故障結果的情況下，對引起故障的原因進行診斷，在相應模型中，快速定位故障位置。同時為準確預測故障的具體位置，在NFPN故障診斷結束時，加入最小割集發生率，對引起故障的所有底層庫所(即最小割集)進行排序，檢修人員可以根據最小割集發生率的大小依次對底層庫所進行排查，避免了維修的盲目性，提高了維修效率。

故障預測公式為：

(5)

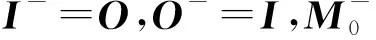
若最小割集為F={f1,f2,…,fn}，則最小割集障發生率為[15]：

(6)

2.3 NFPN的自學習能力

在FPN中，權值反映了輸入庫所對其變遷的影響程度，變遷可信度反映了變遷對其輸出庫所的影響程度。在故障傳播過程中，這兩個值共同反映了故障的傳播能力。但是在電機系統中，故障由變遷傳遞給輸出庫所的過程往往是非線性的，為準確反映故障的傳播能力，利用高斯函數代替經驗化嚴重的變遷可信度，通過改變變遷影響因子模擬實際情況下故障傳播的過程。同時為提高FPN在電機系統的自適應能力，引入BP神經網絡，利用神經網絡的誤差反傳方式對權值ω和變遷影響因子b進行調節，提高算法的適應性和準確性。基于BP神經網絡的自適應學習流程如圖1所示。

圖1 基于BP神經網絡的自適應學習流程圖

定義誤差函數為[16]：

(7)

式中α(pi)為輸出庫所實際置信度值，αE(pi)為輸出庫所期望置信度值。權值的修改量梯度為：

(8)

(9)

(10)

(11)

變遷影響因子的修改梯度為：

(12)

(13)

(14)

3 三相異步電動機的數據處理與模型構建

3.1 故障數據處理

三相異步電動機內部結構復雜，引起故障的原因多樣。為準確提取三相異步電動機的故障特征并建立符合實際的故障模型，采用失效模式分析和FPN相結合的方式分析故障數據并建立符合電機系統的故障關系表[28]。其中庫所代表的故障含義如表1所示。

表1 庫所故障對應表

3.2 三相異步電動機NFPN模型的建立

通過對三相異步電動機的結構與故障的分析，在Labview軟件上建立如圖2所示的三相異步電動機NFPN模型[17]。

4 方法的實現

以“電機繞組絕緣燒毀”、“電機抱軸”為例進行推理分析。

4.1 基于BP的初值確定

參照模糊理論、Petri網理論和歷史統計數據等，對數據進行了相應的處理與規范，并借助專家經驗設定初始庫所置信度、權值、閾值與變遷影響因子。

庫所初始置信度：

α0=(0.87,0.6,0.83,0.89,0.73,0.88,0.72,0.82,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.9,0,0)。

變遷閥值設為0.5。

權值初始值ω1,2=0.4，ω2,2=0.6，ω2,3=0.3，ω3,3=0.5，ω4,3=0.2，ω9,9=0.6，ω10,9=0.4，ω12,12=0.31，ω13,12=0.69，其余權值為1。

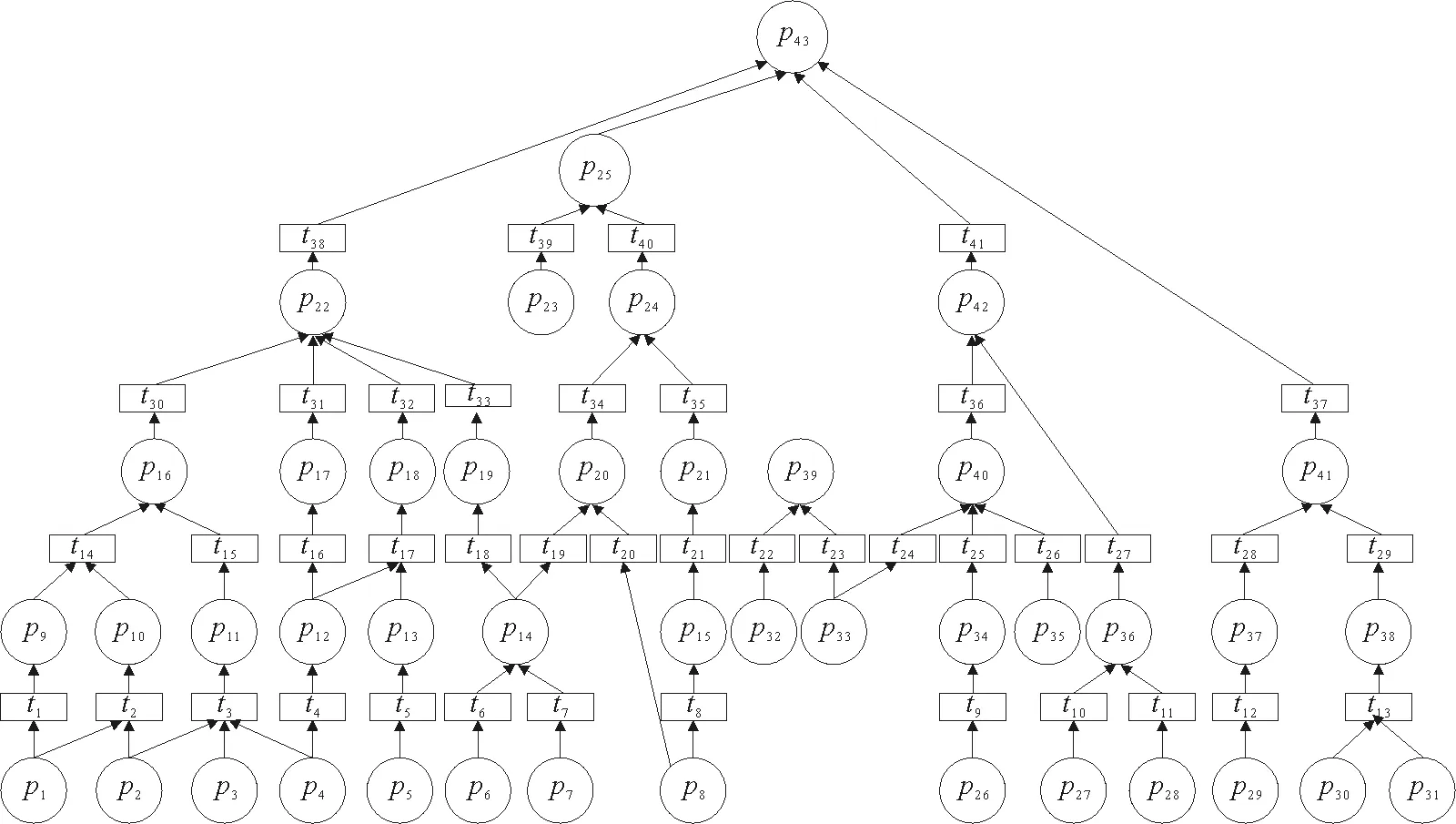
圖2 基于Labview的三相異步電動機NFPN模型

變遷影響因子初始值均設為0.3。

同時，利用BP神經網絡的誤差反傳功能對初始權值和變遷影響因子尋優。為清晰的展現BP神經網絡對權值及變遷影響因子的訓練，以輸入庫所p1、p2、p3、p4影響輸出庫所p10、p11的過程為例，其庫所置信度的期望值為αE(p10)=0.667，αE(p11)=0.732，最大學習步數設為t=2 000，學習率η=0.1，E的最大允許誤差為1×10-3。經過訓練得到圖3～5，分別代表最大允許誤差曲線、權值訓練曲線和變遷影響因子訓練曲線。

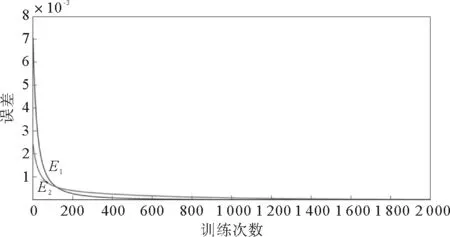
圖3 p9、p10的誤差曲線

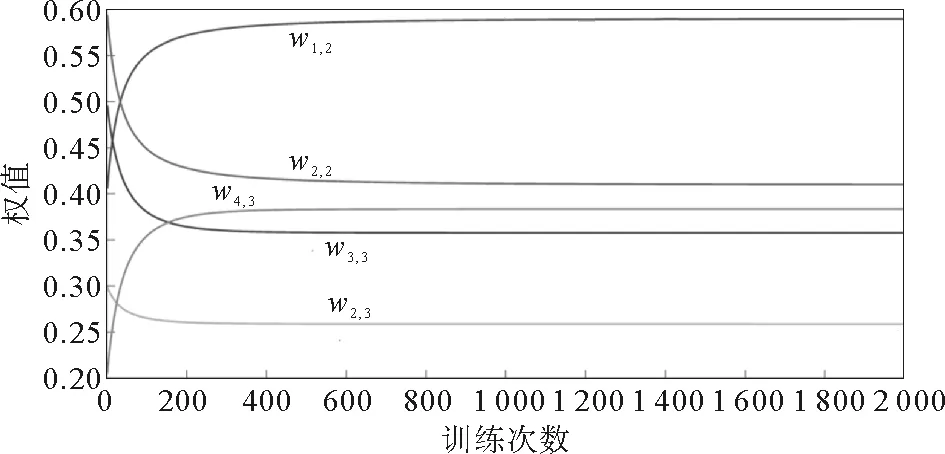
圖4 權值訓練曲線

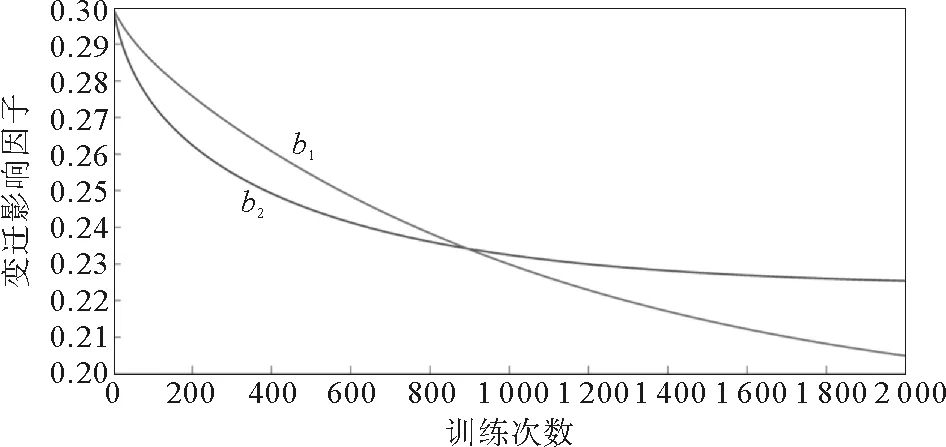
圖5 b1、b2的變遷影響因子曲線

從圖中可以看到在2 000次迭代之后，E1、E2均小于最大允許誤差1×10-3，結果符合要求。通過訓練最終得到調節后的權值:ω1,2=0.590，ω2,2=0.410，ω2,3=0.259，ω3,3=0.358，ω4,3=0.383，ω9,9=0.554，ω10,9=0.446，ω12,12=0.483，ω13,12=0.517。調節后的變遷影響因子為：

B=(0.275,0.225,0.205,0.292,0.176,0.260,0.294,0.260,0.226,0.276,0.246,0.282,0.193,0.228,0.292,0.200,0.247,0.278,0.140,0.208,0.223,0.289,0.291,0.270)。

4.2 故障診斷

假設檢測到“轉子繞組短路”、“電機負載過大”、“熔斷器熔體故障”、“軸封環結構損壞”、“油封材料過熱”等故障。

在此初始標識為M0=(0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)。

根據故障診斷要求，當αk+1=αk時推理結束，αk為最終的庫所置信度向量。

α4=(0.87,0.6,0.83,0.89,0.73,0.88,0.72,0.82,0,0.069,0.727,0.859,0.642,0.848,0,0.592,0.818,0.624,0.811,0.804,0,0.752,0.9,0.738,0.613)，

M4=(0,1,1,1,1,1,0,0,0,0,1,1,1,1,0,1,1,1,1,1,0,1,0,1,1)，

S4=(0,0,1,1,1,1,0,0,0,1,1,1,1,1,0,0,1,1,1,1,1,0,0,1)，

α5=(0.87,0.6,0.83,0.89,0.73,0.88,0.72,0.82,0,0.069,0.727,0.859,0.642,0.848,0,0.592,0.818,0.624,0.811,0.804,0,0.752,0.9,0.738,0.613)，

M5=(0,1,1,1,1,1,0,0,0,0,1,1,1,1,0,1,1,1,1,1, 0,1,0,1,1)，

S5=(0,0,1,1,1,1,0,0,0,1,1,1,1,1,0,0,1,1,1,1,1,0,0,1)。

當α5=α4時推理結束，得到故障診斷信息，其中庫所置信度的值表示該故障可能發生的概率，可以有針對的進行檢查。

4.3 故障預測

當電機出現故障，需要工作人員排查維修時，需要進行故障診斷。假設出現p22即“電機繞組絕緣燒毀”故障。經過推導當M3-=M4-時，推理結束。得到：

M3-=(1,1,1,1,1,1,1,0,1,1,1,1,1,1,0,1,1,1,1,0,0,1,0,0,0)。

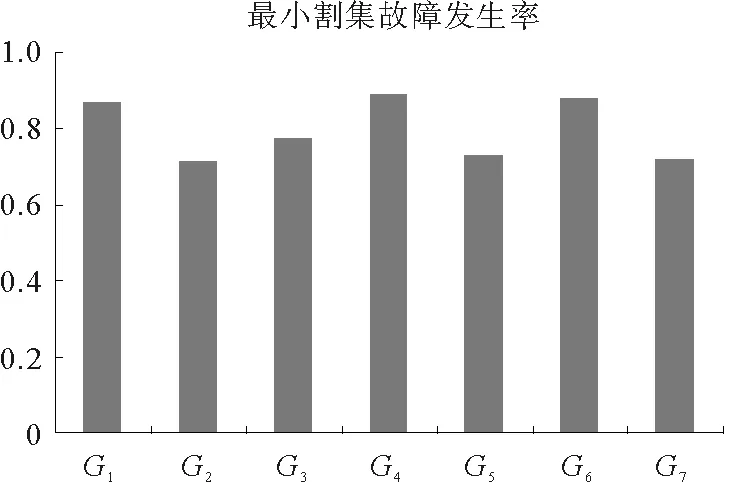
圖6 最小割集故障發生率

推理結束后，采用2.2中所述的最小割集計算方法，來計算P22“電機繞組絕緣燒毀”的最小割集。其割集為：G1={p1}，G2={p1,p2}，G3={p2,p3,p4}，G4={p4}，G5={p5}，G6={p6}，G7={p7}。根據式(6)，得到各個割集的發生率G1=0.87，G2=0.735，G3=0.773，G4=0.89，G5=0.73，G6=0.88，G7=0.72。各個最小割集發生率對應的柱狀如圖6。

在三相異步電動機發生故障時，可根據最小割集故障發生率來依次排查，有效地避免了維修的盲目性并提升診斷的速度。在此實例中，排查的順序為G4，G6，G1，G3，G5，G7，G2。

5 方法的驗證

5.1 有效性驗證

為驗證算法的有效性，引入故障樹方法對三相異步電動機故障診斷的推理結果有效性進行驗證[18]。其中故障樹中各個事件所代表的故障含義如表1所示。在此，以“轉子繞組短路”、“電機負載過大”、“熔斷器熔體故障”為例進行驗證對比。首先，建立“電機運行過熱”故障樹如圖7。

將庫所置信度、權值、閾值和Petri網觸發規則引入故障樹。根據觸發規則，其中X1×ω1,2+X2×ω2,2=0+0.6×0.41=0.246<0.5，不滿足變遷觸發條件，X5不被觸發。需要注意的是，依據Petri網特性，X5與X6組成的與邏輯和X7為競爭關系，需要選取其中的最大值。最后推導得到X8的置信度，X8=0.592，計算結果與NFPN的計算結果相吻合，證明本算法的有效性。

圖7 電機運行過熱故障樹

5.2 準確性驗證

為驗證算法的準確性，與文獻[18]中的算法進行對比，結果如表2所示。

由表2的結果對比可以發現，FFPN和NFPN算法都可以準確地診斷出故障位置，相比于FFPN診斷算法，本算法的故障診斷結果具有更好的準確性；同時，故障診斷參數經過BP神經網絡算法的調整，保證了不同故障情況下的檢測準確性均在80%以上，克服了FFPN算法由于賦值經驗化導致適應性差的問題。因此，通過上述比較可以證明本研究所提出的方法能夠滿足電機系統的故障診斷要求。

表2 故障診斷結果對比

6 結論

本研究將BP神經網絡與FPN融合，提出NFPN的方法，并將其應用于三相異步電動機電機系統的故障診斷，結論如下：

1) 通過在NFPN中引用高斯函數以及變遷影響因子反映變遷對輸出庫所的影響程度，并利用BP神經網絡對權值和變遷影響因子進行調節，提高了算法的準確性和適應性。

2) 建立了三相異步電動機的NFPN模型，通過FMES與FPN相結合的方式，得到三相異步電動機的故障關系；同時利用故障診斷和預測方式確定故障源的位置，有效避免了檢修和維護工作的盲目性。