交通量持續增長下既有拱橋車載效應極值概率

余浩然，魯乃唯，劉揚

(長沙理工大學 土木工程學院,湖南 長沙 410114)

據交通運輸部公布的數據，中國 2018年公路貨運量同比增長7.3%。其中：新疆維吾爾自治區公路貨運量的增長率高達13.7%，遠高于歐盟等發達國家(1.5%～2%)的。隨著中國公路車流量和車載重量的持續增長，超載已成為導致橋梁垮塌的主要原因之一[1]，橋梁的實際車流荷載或已超出設計值。中國現行《公路橋涵通用設計規范(JTG D60—2015)》[2]將車道荷載中集中荷載 Pk的起始計算標準由180 kN提高至270 kN。因此，在中國公路貨運量長期保持增長的趨勢下，研究交通量持續增長下橋梁車載效應極值概率是準確評定既有橋梁運營安全的一個重要內容。

橋梁運營期內車載效應極值概率分析是橋梁工程領域的研究重點，也是橋梁安全驗算的重要內容。通常的研究思路為：先基于WIM數據模擬隨機車流；其次，求解荷載效應時程曲線，并提取最大效應值；再采用極值外推方法(如：GEV分布、Rice公式及Nowak法等[3])，外推一定重現期內的效應最大值。

基于WIM數據的公路橋梁車載效應極值概率研究不僅適用于評定既有橋梁的運營安全，也可用于校驗既有設計的車載模型。例如：Soriano[4]等人在紐約等多地的WIM監測數據的基礎上，對典型小跨徑橋梁的荷載效應進行了外推分析。Enright[5]等人采用歐洲4個國家的WIM監測數據，重點研究了中、小跨徑橋梁的交通荷載效應極值外推和標準值，并分析了車輛動力效應、多車效應及超載影響等。其研究結果為歐洲EC-LM1規范的修訂提供了基礎。張喜剛[6-11]等人對中國多個地域國道和高速公路的WIM數據進行了統計分析與極值外推，研究了適用于中國交通荷載特點的車輛荷載模型，其結果表明：實測車流荷載在橋梁運營安全評估中具有重要性。因此，作者擬提出基于“時間劃分-極值概率累加”的極值概率分析方法，采用改進的GEV分布捕捉車載效應的時變特征，經算例驗證該方法的適用性；并基于WIM實測車流數據預測交通量增長和超載率限制下既有拱橋的最大彎矩，分析交通量增長和超載率限制對橋梁車載效應極值的影響。

1 橋梁時變極值外推方法

1.1 經典GEV分布的極值外推理論

根據經典極值理論，獨立同分布的隨機變量的最大值分布可采用GEV分布來描述。GEV分布是一種包含Gumbel分布、Weibull分布和Frechet分布的一般形式。其極值的累積分布函數(cumulative distribution function, 簡稱為CDF)可表示為：

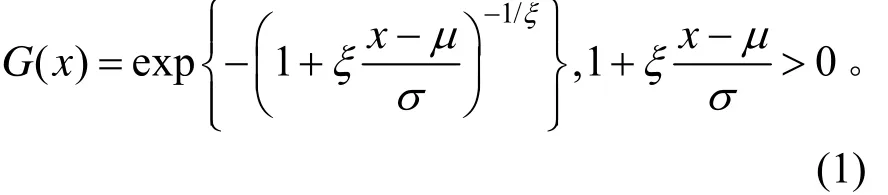
式中：μ,σ和ξ分別為分布函數的位置、尺度和形狀參數，且μ,σ和ξ均大于0。

當ξ=0時，函數的分布為Gumbel分布；當ξ＞0時，函數的轉換為 Frechet分布；當 ξ＜0時，函數的轉換為Weibull分布。

針對橋梁車輛荷載極值的問題，處理極值數據的常見方法是將數據分組為具有相同持續時間的區間，并提取每個區間內最大值來擬合GEV分布。如：某橋梁的日最大效應值為Xi，則該橋梁在n d內的最大效應值為：

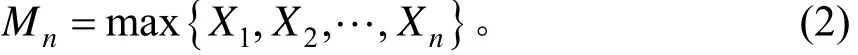
式中：Xi為服從獨立同分布的隨機變量。

假定Xi的分布函數為F(Xi)，則Mn的分布函數可表示為：

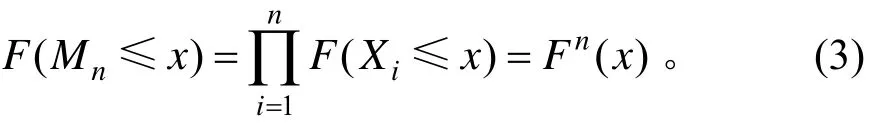
1.2 基于交通量區間增長模型的改進GEV分布

交通量的增長會導致橋梁車載效應轉換為非平穩隨機過程，經典極值外推方法無法給出準確的外推值。因此，本研究提出了改進的 GEV分布，研究交通量區間增長下橋梁車載效應極值概率。交通量區間增長的極值概率模型如圖1所示，其表達式為：

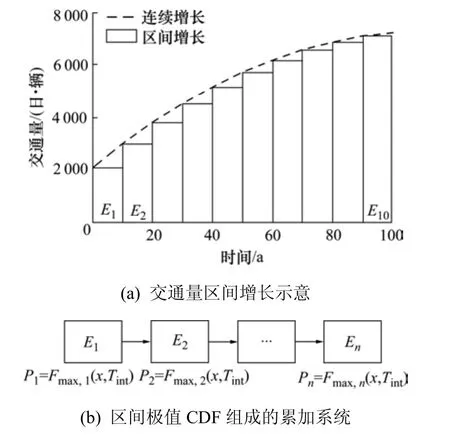
圖1 考慮交通量區間增長的極值概率模型Fig. 1 Extreme probability model considering the growth of traffic volume interval

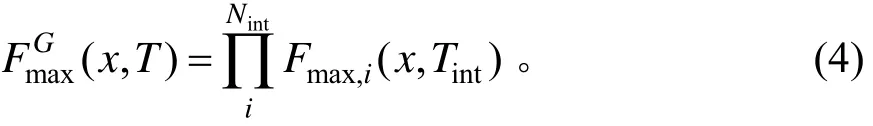
在圖1中，Ei為第i個區間內的極值；Fmax,i(x,Tint)為第i個時間區間Tint內荷載效應x的極值概率分布函數；Fmax(x,T)為橋梁運營期T時間內x的最大值。

2 算例分析

2.1 車重極值的外推分析

在Leahy[12]等人給出的經典算例基礎上，采用改進的GEV分布，外推Rt=1 000 a時車輛總重的最大值。

算例：取100 a樣本數據，每個時間區間時長為1 a，考慮每年的工作日有250 d，交通量為1 000 veh/d，車輛總重服從正態分布N(50 t，5)，假定貨車數量年增長率R為4.1%。分析結果如圖2所示。

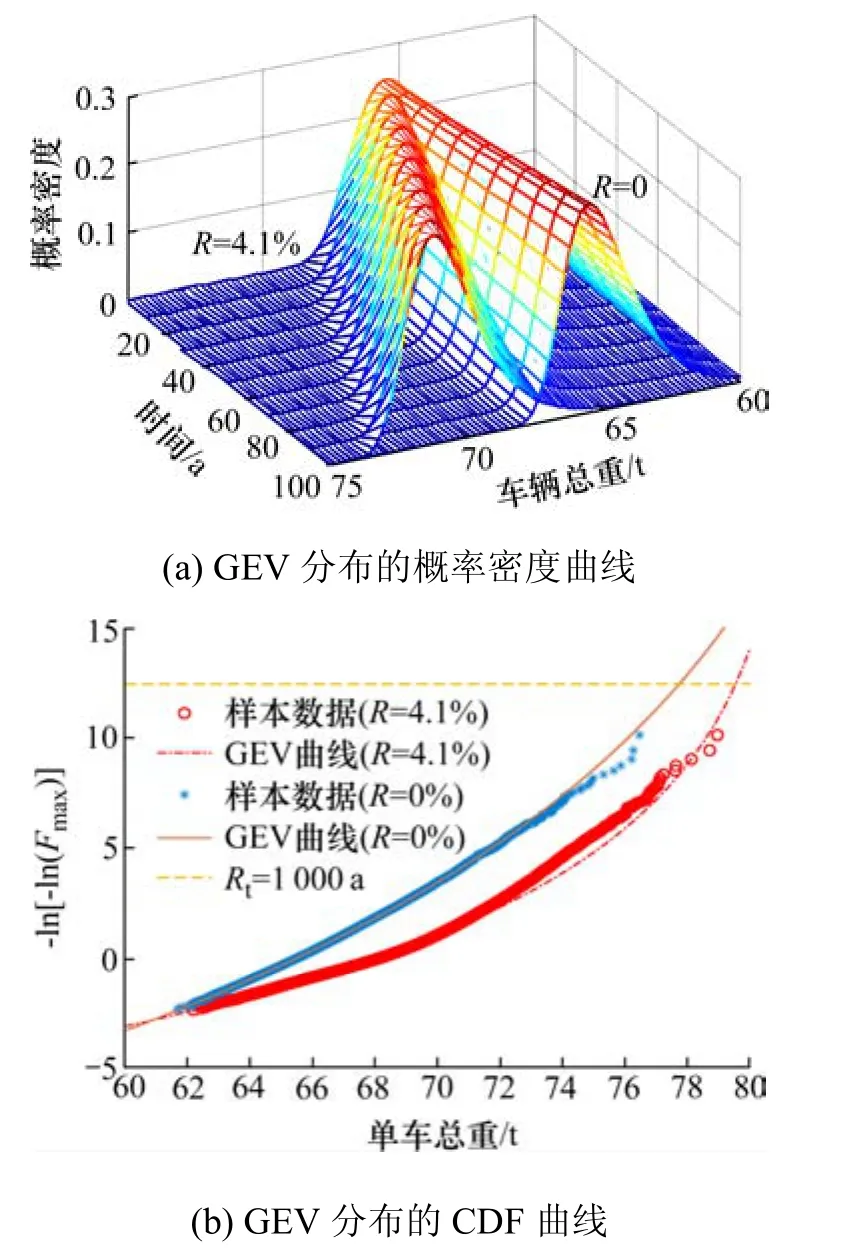
圖2 算例的計算結果Fig. 2 Calculation result of the example

從圖2(a)中可以看出，車重極值概率密度(PDF)曲線隨時間變化和交通量增長呈現顯著偏移，表現了時變非平穩特征。從圖2(b)中可以看出，GEV分布曲線隨交通量增長呈現顯著偏移，經典的 GEV分布外推值失真；而采用“時間劃分-極值概率累加”的改進 GEV分布可給出較為準確的外推值。該算例驗證了該方法可適用于解決車載效應時變極值外推問題。

2.2 交通量持續增長的極值外推分析

在分析算例的基礎上，根據WIM實測車流數據，提出了“時間劃分-極值概率累加”的方法。采用基于交通量區間增長模型的改進 GEV分布外推車載效應最大值，分析步驟如圖3所示。

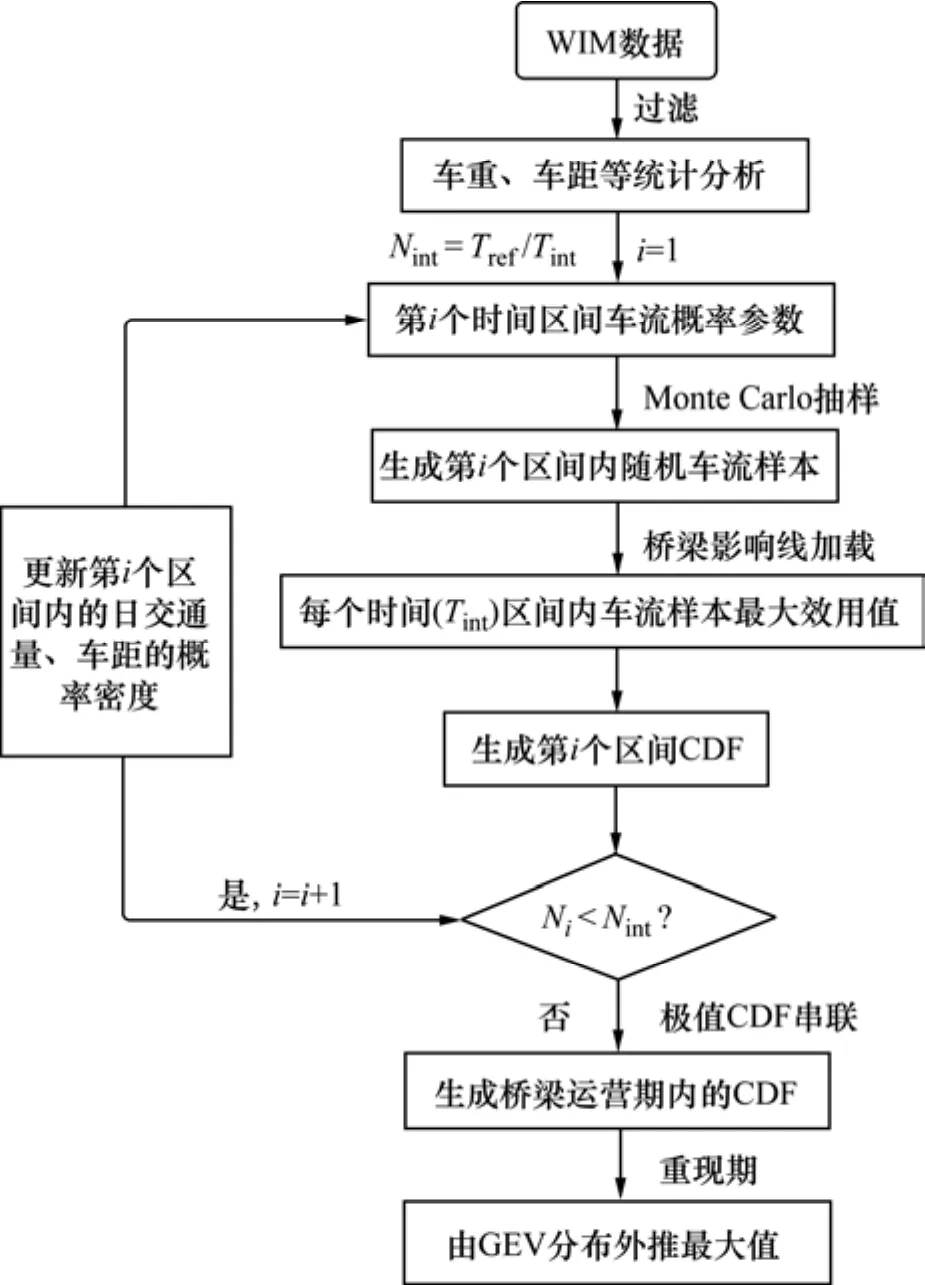
圖3 交通量持續增長的極值外推分析流程Fig. 3 Extreme value extrapolation analysis process for continuous growth of the traffic load

在圖3中，其步驟為：①劃分區間的數量和長度。基于WIM數據，建立第一個時間區間的車流概率模型，由交通量區間增長模型不斷更新其后的車流概率模型。②逐步將每個時間區間內的隨機車流模型加載至影響線并求解荷載效應時程曲線，再提取每個時間區間 Tint內的最大效應值。③將每個區間內的極值 CDF進行累加，根據累加后的極值概率模型外推一定重現期的最大值效應。其分析結果的精度與效率取決于區間的長度和數量。若一個時間區間被認為是足夠小的(如：1 d)，即假設1 d中交通量是穩定不變的[13]，則在該時間區間內的時變性可以被忽略，分析的結果近似于精確解；若劃分區間長度過大，則計算結果可能失真。因此，區間長度和數量的選擇決定了外推精度。

3 工程實例

3.1 工程背景

某拱橋位于湖南省，其主跨為 60 m，矢高為10 m，拱軸系數為 1.662。設計汽車荷載為公路Ⅱ級。該拱橋平均車流量約為1 140 veh/d，6軸車貨車占比為15.49%，車型比例和車重概率分布見文獻[14-15]。橋梁的有限元模型如圖4所示。

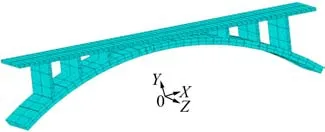
圖4 有限元模型Fig. 4 Finite element model

3.2 隨機車流作用效應分析

為了建立該拱橋彎矩極值概率模型，提取了10 kN移動力作用下主拱圈跨中節點彎矩影響線，如圖5所示。從圖5中可以看出，車輛加載至L/4跨和3L/4跨節點時會產生最不利彎矩。將隨機車流模型加載至主拱圈跨中節點彎矩影響線并求解其時程曲線，再提取日區間的最大效應值，如圖6所示。

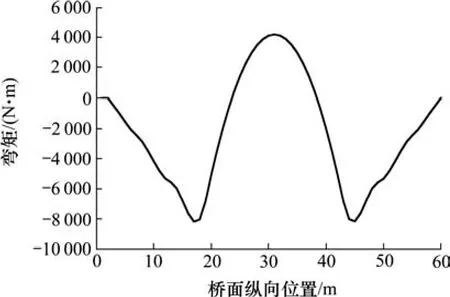
圖5 主拱圈跨中彎矩影響線Fig. 5 The influence line of the main arch ring mid-span bending moment

3.3 交通量的增長對車載效應極值的影響

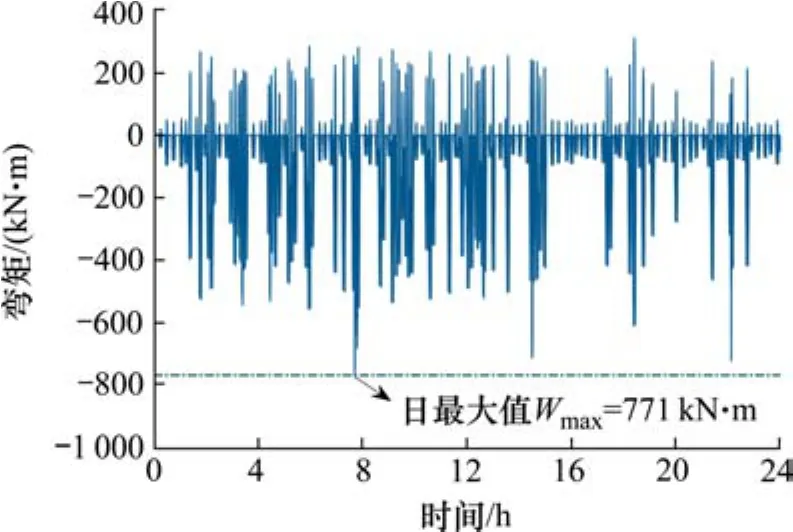
圖6 隨機車流作用下主拱圈跨中彎矩時程曲線Fig. 6 Time-history curve of the mid-span bending moment of the main arch ring under random traffic flow

用公路Ⅱ級汽車荷載模型計算出拱橋主拱圈跨中節點的設計車輛荷載作用彎矩標準值 Md約為1 416 kN·m。本研究假定年交通量增長率R=0%,2%和4%，取10 a的樣本數據，每個時間區間時長為1 a，每年工作日取250 d。基于圖6中的彎矩時程曲線，采用考慮交通量區間增長的改進 GEV分布外推Rt=2 000 a的主拱圈跨中彎矩的最大值。其結果如圖7所示。

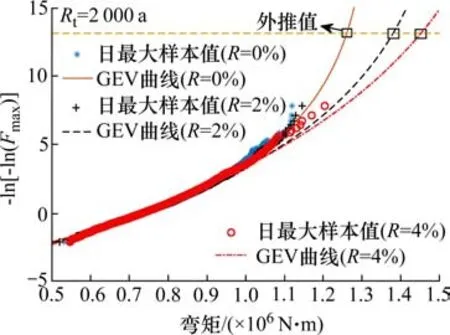
圖7 交通量的增長對拱橋極值外推的影響Fig. 7 Impact of traffic growth on extreme extrapolation of arch bridges

從圖7中可以看出，交通量的增長會導致橋梁車載效應極值的顯著增大。當年交通量增長率為0%,2%和4%時，該拱橋在Rt=2 000 a對應的彎矩的最大值分別為1 261,1 383和1 455 kN·m，與設計標準值的比分別為0.88,0.97和1.02。當年交通量增長率為 2%～4%時，既有拱橋的彎矩的最大值增加10%～15%。當年交通量增長率為 4%時，該拱橋的彎矩的最大值將大于其設計標準值。表明：需要對橋梁車流量進行交通管制。

3.4 超載率對車載效應極值的影響

由該算例的分析可知，在未控制超載車輛時，該拱橋的彎矩的最大值為1 455 kN·m(R=4%)。假定車輛的超載率 α(實際超載重量與限載重量的比例)控制上限為200%,100%和50%，僅保留隨機車流中未超出該比例的車輛，取年交通量增長率 R=4%，重新模擬車流過橋梁響應極值，其結果如圖8所示。

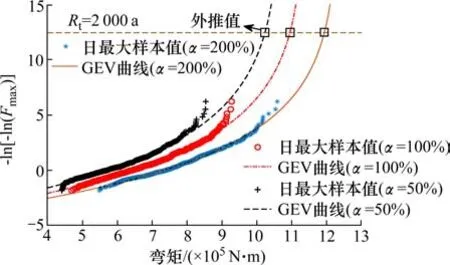
圖8 超載率的限制對拱橋極值外推的影響(R=4%)Fig. 8 Effect of overload rate limitation on arch extrapolation(R=4%)

從圖8中可以看出，超載率的限制對橋梁車載效應極值有顯著影響。在年交通量增長率確定的情況下，嚴格控制超載率上限，車載效應極值顯著減小。當車輛的超載率 α控制上限為 200%,100%和50%時，該拱橋在Rt=2 000 a對應的彎矩的最大值分別為1 194,1 096和1 023 kN·m，與其設計標準值的比分別為0.82,0.75和0.70。當超載率上限為50%～200%時，既有拱橋的彎矩的最大值減小至 70%～82%。表明：交通量的增長和超載率的限制對橋梁荷載效應極值的影響較大。在預測橋梁荷載效應極值時，應考慮交通量增長和超載率的影響。

4 結論

1) 典型算例分析結果表明：在考慮交通量增長的情況下，經典的GEV分布外推值失真，而基于“時間劃分-極值概率累加”的改進 GEV分布可給出較為準確的外推值。

2) 某拱橋的算例分析結果表明：交通量的增長會導致橋梁車載效應極值的顯著增大。當年交通增長率為 2%～4%時，既有拱橋的彎矩的最大值增加10%～15%；當年交通增長率為 4%時，該拱橋的彎矩的最大值將大于其設計標準值，應對橋梁車流量進行交通管制。

3) 當超載率上限為50%～200%時，既有拱橋的彎矩的最大值減小至 70%～82%。超載率的限制對橋梁車載效應極值有顯著影響。在年交通量增長率確定的情況下，嚴格控制超載率上限，顯著減小了橋梁車載效應極值。