海洋起重機沖擊載荷研究

郭宏亮 隋振華，2

1 上海振華重工(集團)股份有限公司2 中交公路長大橋建設國家工程研究中心有限公司

1 引言

隨著起重機的大型化、高速化和輕量化發展，其動力學研究顯得愈發重要。起重機的沖擊載荷問題是指鉤頭部分突然加載或卸載引起的臂架頭部載荷顯著變化，如起吊物從靜止到穩態上升過程中速度增加，導致鋼絲繩拉力增大。這會導致起重臂的彈性勢能做功，引起應力的增加，甚至發生傾覆。

研究沖擊載荷，探究其形成的理論原因，將對工程設計具有積極的意義。本文從力學原理上研究沖擊導致載荷增大的原因及相應的計算方法，并通過有限元計算對推理過程進行驗證。

2 起升載荷沖擊現象及理論分析

如圖1所示，起重機的起吊模型可以簡化為一個質量為M的重物及垂直牽引它剛度為K的鋼絲繩。

圖1 起吊模型

沖擊問題因速度變化而產生。當速度為0時，鋼絲繩被穩定拉伸，其拉力等于重力Mg。當速度由0突然變為V時，根據振動理論，可以得出動力學方程：

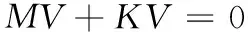
(1)

求解該方程，即可得圓頻率:

(2)

故重物自由振動的振幅為:

(3)

因此，在振動過程中，鋼絲繩的最大拉力為自由振動達到最大振幅(即鋼絲繩具有最大拉伸量)時的拉力：

(4)

為方便應用，可用沖擊系數φ來描述這一現象。

(5)

從式(5)可以看出，影響沖擊載荷(沖擊系數)的主要原因包括穩態起升速度V，懸吊系統剛度K及懸吊物質量M。起升速度V主要來源于電機和卷筒，海浪導致的船體運動(垂蕩和縱搖)等，其為沖擊載荷的外因。懸吊系統的剛度K則取決于起重機的固有結構，是內因。

3 起重機的剛度計算

從整體概念說，懸吊系統包括牽連重物的鋼絲繩及起重機的鋼結構，因此起重機的剛度可以分解為以下4個部分(見圖2)：

(1)起升系統K1，主要指直接連接吊重的鋼絲繩。

(2)俯仰繩+臂架系統K2，這一部分的剛度主要指俯仰繩的伸長和臂架的變形。

(3)人字架或桅桿系統K3。

(4)筒體部分K4。

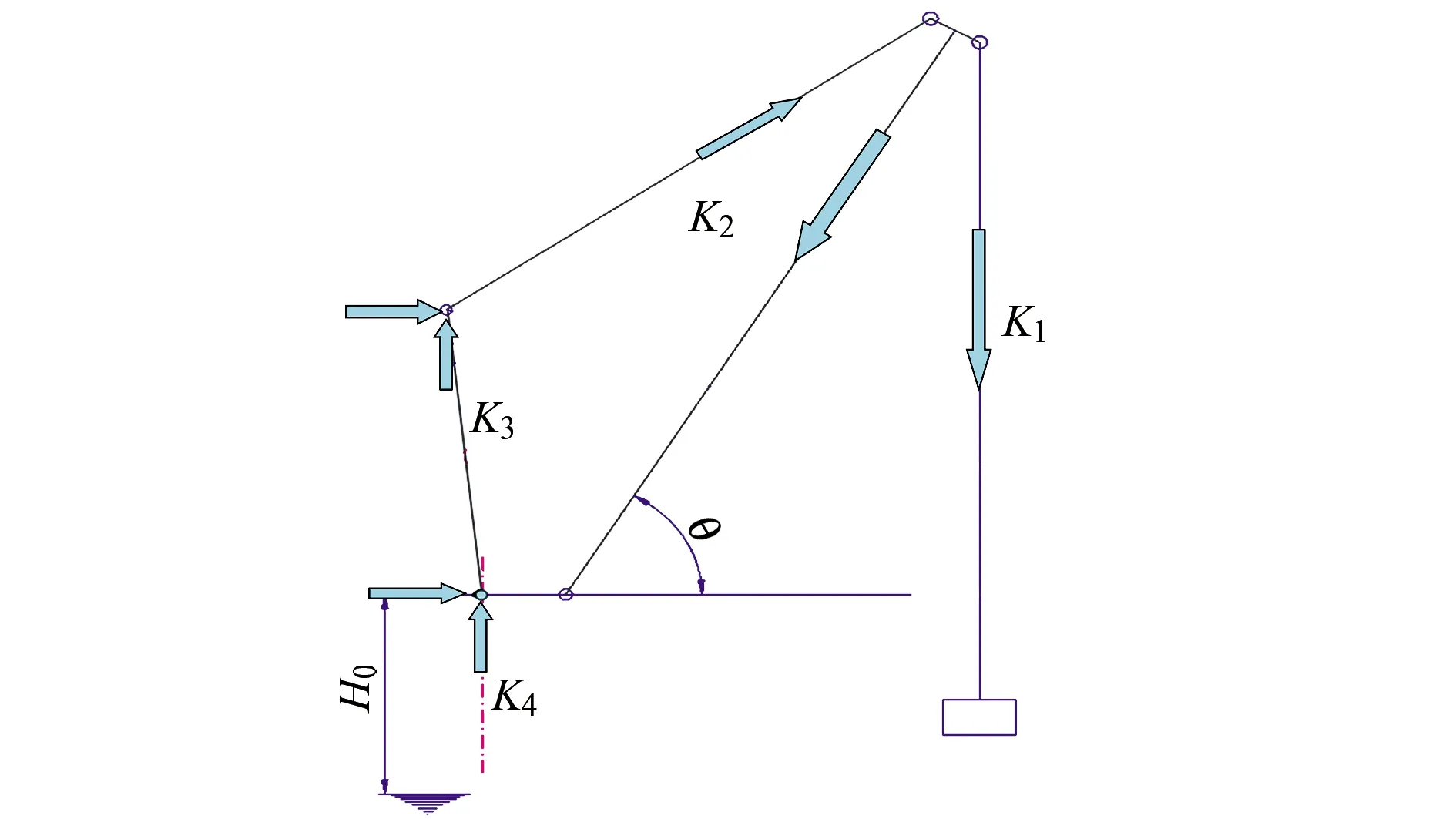
圖2 起重機剛度分解

3.1 起升系統

起升系統主要是指起吊載荷的鋼絲繩。起升系統通常由2個連貫的部分組成，一個是卷筒端到臂架頭部的單根部分，另一個是臂架頭部吊鉤定動滑輪之間的多倍率部分。當吊鉤處滑輪纏繞倍率較小時，卷筒端到定滑輪部分的變形對整體影響比較大，這常見于較小的吊鉤。

如圖3所示，單根鋼絲繩從卷筒端R0，繞經滑輪R1，R2，R3，到達臂架頭部定滑輪組R4，然后通過滑輪組增大倍率到達吊鉤端的R5。

考慮單根鋼絲繩截面積為A，彈性模量E，從R0端到R4端的總長度為L04，從R4到R5端高度為L45，吊鉤端的倍率為n，吊鉤處作用的垂直載荷為F。則L04的伸長量為：

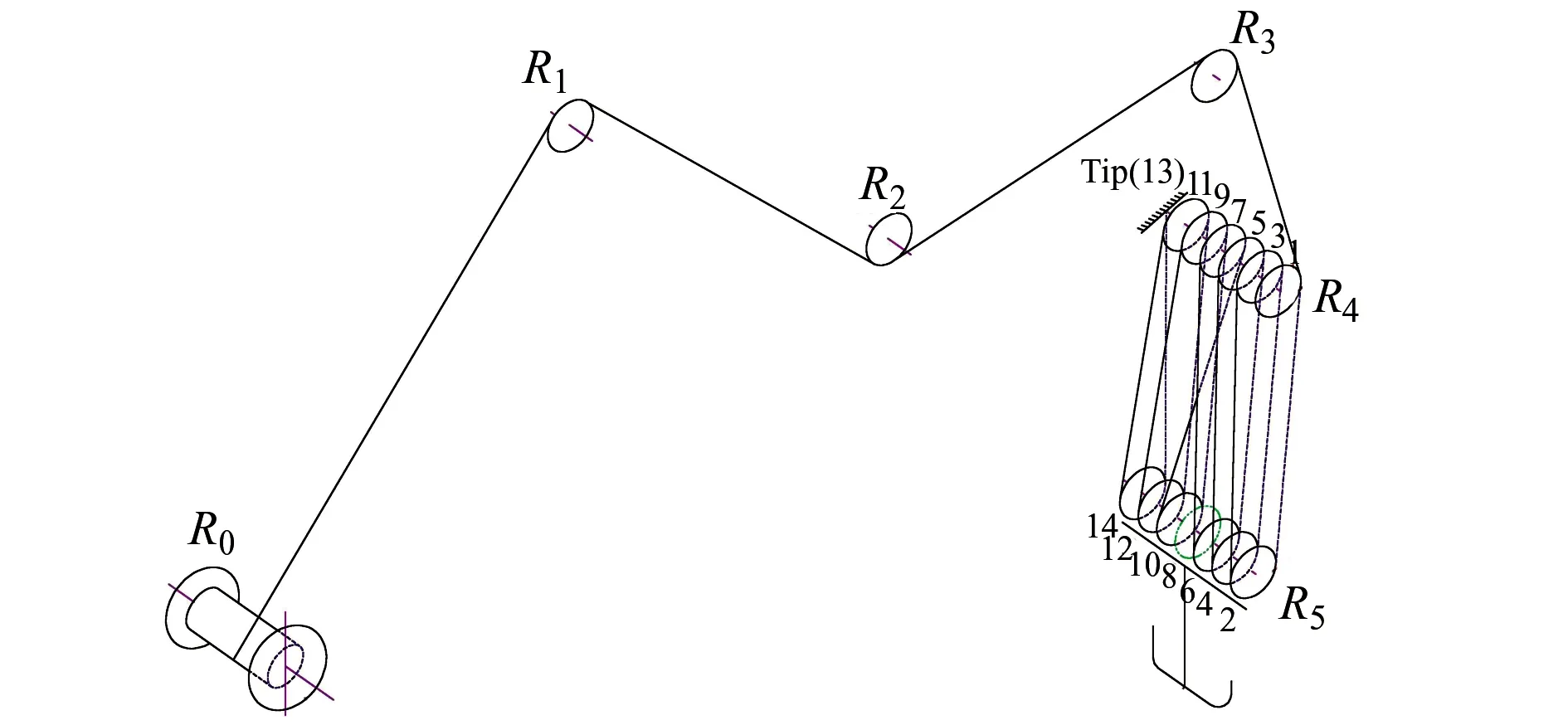
圖3 起重機起升系統

(6)

L45的伸長量為：

(7)

L04導致的鉤頭向下位移量將被滑輪組倍率稀釋為Δ04/n，所以，起升系統部分導致的鉤頭向下位移量為：

(8)

起升系統的剛度為：

(9)

3.2 俯仰繩+臂架系統

在空間上，俯仰繩(L12)和臂架(L02)構成了一個三角形，維系著臂架鉛垂平面的穩定(見圖4)。俯仰繩受拉，端點下移，臂架受壓，端點后移。

圖4 俯仰繩+臂架系統

可以用解析這個三角形的辦法獲得相應剛度，臂架頭部的變形計算如下。

根據軸向力變形公式計算變幅繩的伸長量：

(10)

根據軸向力變形公式計算臂架的軸向壓縮量：

(11)

由上，可計算出鉤頭受力變形后的變幅繩長度L′12=L12+Δ12，臂架長度L′02=L02-Δ02。根據P0、P1坐標和新的變幅長度L′12和臂架長度L′02，計算臂架頭部P2的新坐標(X′2，Y′2)。變幅和臂架系統在外力F作用下，引起的臂架頭部下移量為Δ2=Y′2-Y2。其中Y2是變形前臂架頭部的縱坐標。可得俯仰繩+臂架系統剛度為：

(12)

3.3 人字架或桅桿系統

人字架或桅桿用來撐起俯仰繩的上端點，在比較大型的起重機，一般采用人字架(A架)的形式，因為是三角布局，整體剛度比較好。在近海起重機中，為了節約空間，經常做成桅桿形式，桅桿上細下寬，桅桿整體成懸臂梁形式，在俯仰繩拉力作用下，頂端更容易變形。

當變幅繩水平分力比較大時，人字架或桅桿頂端向前位移，從而導致變幅臂架三角形整體向前向下傾轉，使臂架頭部產生向下位移Δ3。可得人字架或桅桿系統剛度為：

(13)

3.4 圓筒體部分

圓筒體坐落于人字架之下，在近年發展的風電安裝平臺中，筒體經常是高度方向的尺寸遠大于直徑，這使得筒體作為一個懸臂梁，其末端彎曲變形不可忽略。

圓筒體部分的受力特征以垂直方向的壓力和向前的傾覆為主要特征，可通過計算壓彎變形獲得筒體頂端的垂直變形量以及傾覆平面內的角變形量。根據角變形及起重機整體尺寸，繼而可以求得其引起的臂架頭部的垂直變形量Δ4，可得圓筒體部分剛度為：

(14)

3.5 起重機的整體剛度

各分項剛度K1，K2，K3和K4成串聯關系，統合起來，起重機的整體剛度為：

(15)

4 起重機整體剛度計算的有限元驗證

用有限元方法也可以獲得起重機的剛度。建立包含圓筒體在內的起重機模型，在臂架頭部施加垂直向下一個單位的載荷，靜態計算該載荷引起的位移Δ234，則1/Δ234即為起重機鋼結構貢獻的剛度。

前述過程從理論上推導了起重機剛度的組成部分，為了驗證其準確性，對某600 t起重機不同臂架仰角下的剛度用前述理論和有限元模型分別進行計算，計算結果比較見圖5。

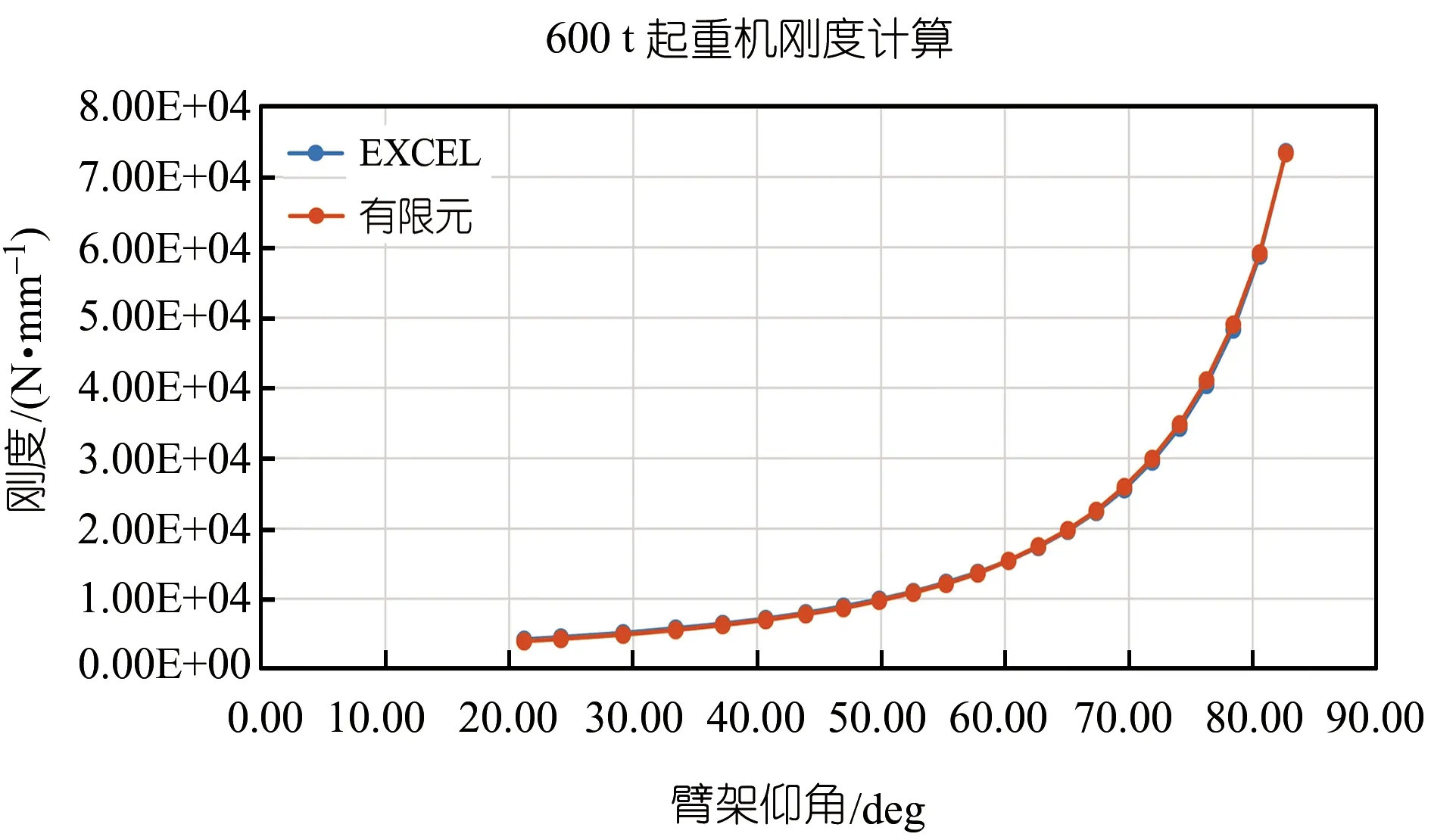
圖5 起重機剛度有限元計算和理論計算比較

由圖5可見，理論計算結果和有限元計算結果吻合度非常高，證明上述推導的理論計算是可行的。理論計算公式可以編制為EXCEL程序，通過簡單的幾個輸入參數，就可以迅速獲得起重機的整體剛度值。這可省去繁瑣的有限元建模過程，提高工作效率。

5 結語

隨著起重機向高速化、大型化、輕量化發展，起重機的載荷沖擊問題受到更多的重視。從理論上著手，分析了沖擊載荷背后的結構動力學原理，分解了起重機的剛度組成，相應地提出了剛度計算的公式方法，經有限元分析證明計算方法的正確性，為起重機的剛度計算提供了更加快捷的途徑。