基于自由曲面的高倍率廣角顯微目鏡設計*

郭雨桐 常軍? 胡瑤瑤 鐘樂 宋大林

1) (北京理工大學光電學院, 北京 100081)

2) (公安部第一研究所, 北京 100048)

隨著顯微鏡性能的不斷提升, 要求顯微目鏡具有更大的視場、放大倍率以及更好的成像質量.顯微目鏡由于孔徑光闌外置, 且焦距較短, 其設計難點在于如何校正大視場帶來的畸變與其他軸外像差, 并在此基礎上獲得符合人眼觀察要求的出瞳距離.本文分析了目鏡光學系統存在的主要像差, 特別是帶有畸變的光學系統對成像所產生的影響.將自由曲面應用在顯微目鏡光學系統畸變校正中, 設計出一款視場角達到60° (即± 30°), 放大倍率達到25× 且全視場畸變小于5%的高倍率廣角顯微目鏡.采用五片三組元式結構, 其中自由曲面鏡片采用塑料材料且關于XOZ與YOZ平面對稱, 實現了結構簡單、易于加工且成本較低的高性能顯微目鏡設計.

1 引 言

隨著各研究領域的深入, 對重要研究工具—顯微鏡的性能要求也逐漸提升.目鏡廣泛應用于顯微鏡等目視光學系統中, 其功能和設計方法與成像物鏡有很大的不同.目鏡需要在人眼可接受的范圍內, 將一定距離處的放大圖像呈現出來, 因此目鏡的出瞳必須外置, 并且具有一定的出瞳距離以滿足人眼觀察的需求[1].為滿足更加復雜的實驗要求,需要目鏡的觀察視野更大, 放大倍率更高, 以與具有較大線視場的顯微物鏡相匹配.普通目鏡的視場角在 30°左右, 而廣角目鏡通常是指視場角在50°以上的目鏡[2].大視場為目視光學系統引入更大的畸變, 8%—12%的畸變在廣角目鏡中都是很常見的現象[1], 所以需要運用更加復雜的光學結構來加以校正.自由曲面的應用對畸變具有良好的校正效果, 并且能夠簡化光學系統結構, 減少所需透鏡片數[3,4].

自由曲面擬合通常是利用假想為曲面上的一組離散點, 尋找形式比較簡單、性能良好的曲面的解析表達式.曲面的解析表達式采用參數形式來表示, 這種形式允許多值曲面用統一的形式來表示,且和坐標系的選取無關.曲面通常采用數學方程式來定義, 常見自由曲面面型描述方法包含B樣條曲面、Bezier曲面、NURBS法等[5].隨著塑料材質鏡片的出現以及加工技術的進步, 自由曲面的加工變得越來越切實可行[6?9].和傳統球面光學相比較,自由曲面光學具有以下特點:

1)提供更多的設計自由度, 光學面型可由非對稱、不規則、復雜的自由曲面隨意組合而成[2];

2)采用先進的數控超精密制造技術, 直接加工出自由曲面光學面, 被加工面可以達到亞微米量級面型精度與納米量級表面粗糙度[10];

3)采用光學塑料等新材料技術, 大批量生產光學組件[11,12].

自由曲面在非成像系統的應用主要包括: 激光整形[13,14]、汽車照明[15]、LED 均勻照明等[16,17].隨著研究的深入, 自由曲面的研究慢慢延伸到了成像領域, 如離軸反射系統[18,19]、頭盔顯示器[20]、自由曲面微透鏡陣列[21]和全景光學系統[22]中, 用來校正光學系統的各種像差.

本文采用五片三組元式結構, 設計出一款結構簡單、且具有高放大倍率與較高成像質量的廣角顯微目鏡.采用一片塑料自由曲面透鏡對小孔徑、大視場顯微目鏡系統中的畸變進行校正, 極大地簡化了光學系統結構, 獲得了良好的效果.

2 理論研究

廣角目鏡的工作波段設計為486—656 nm, 以便于目視觀察.人眼內虹膜中心的瞳孔為光線進入眼睛的通道, 在目鏡光學系統中相當于孔徑光闌.瞳孔括約肌的收縮與擴張可以使瞳孔縮小與擴張從而控制進入瞳孔的光量.一般人眼瞳孔直徑可變動在1.5—8 mm之間, 考慮到顯微鏡視場的照明強度等因素, 一般將顯微目鏡出瞳直徑設置為1—2 mm.

顯微目鏡焦距與放大倍率間的關系為

故目鏡焦距越短, 放大倍率越大.而顯微鏡的觀察方式又要求一定的出瞳距離, 故如何兼顧放大倍率與適當的出瞳距也是本設計的難點.為便于觀察且免除人眼睫毛的影響, 一般要求顯微目鏡的出瞳距離大于 6 mm, 本設計出瞳距離為 7.4 mm, 滿足目鏡設計要求.

目鏡系統的調焦距離計算公式為

目鏡光學系統的典型結構如圖1所示, 由于目視觀察的特殊性, 系統的孔徑光闌外置, 對出瞳距離的大小有一定的要求.這導致軸外光線在各透鏡上的入射角與入射高度較大, 為系統引入了較大的軸外光線像差.

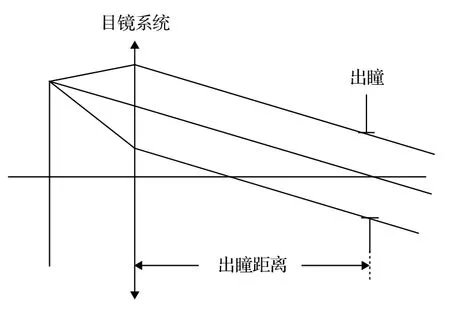
圖1 目鏡光學系統示意圖Fig.1.Schematic diagram of eyepiece.

為便于分析, 把像差展開為孔徑和視場的級數[5].那么軸外點的像差空間分量可以表示為

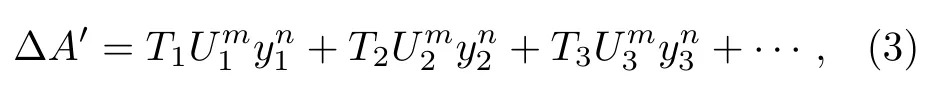
其中 ? A′代表某一種像差; T1, T2, T3為各級像差系數; y 代表像高, 與視場成正比; U 代表孔徑; m ,n 為常數;為初級像差,為二級像差, 以此類推.

只保留到二級像差, 大視場小孔徑光學系統中彗差、細光束場曲、畸變的級數展開式為

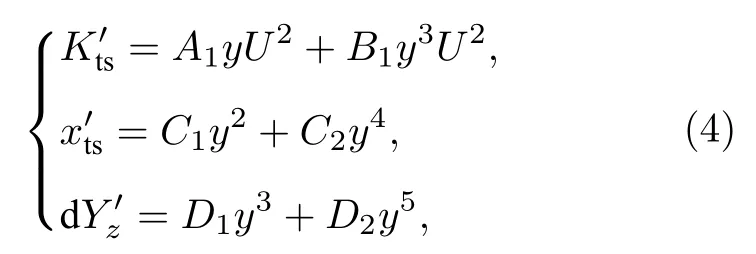
基于光學硬件校正畸變的要點在于改變每一個視場的光線的最終出射方向, 使得每個視場的光線最終到達無視覺畸變所對應的新像點.對具有畸變的光束結構進行分析, 即可得到成像光線與理想像點的偏離量.

設物面坐標為x, y; 入射光瞳面上的坐標為h, z.由于存在像差, 其通過光學系統后的共軛光線與子午面的交點并不在高斯像面上.d Y′和 d Z′分別表示子午垂軸像差和弧矢垂軸像差分量.把 d Y′和dZ′展開成 y , x , z 和 h 的級數, 推導出空間光線初級像差的表達式為[5]

其中 Ah, Bh, Ch, Dh為公共因子, 對于每個折射面來說是一個不變量; SI , S II , S III , S IV , S V 為塞德和系數.

用極坐標來表示入射光瞳面上光線的坐標, 如圖2所示, 可得極坐標表達式為

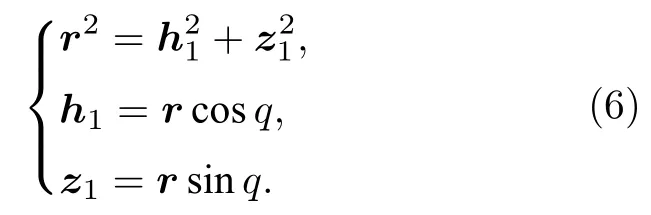
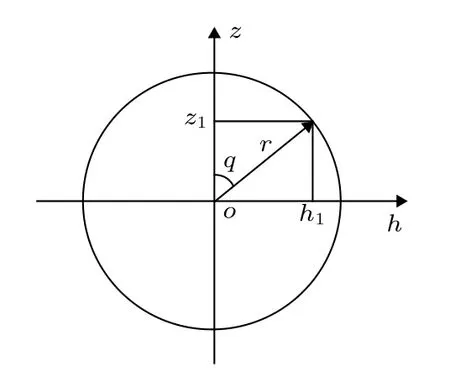
圖2 入射光瞳面上光線坐標Fig.2.Coordinates of ray on the entrance pupil surface.

將(6)式代入(5)式可得初級像差的極坐標表達式如下:

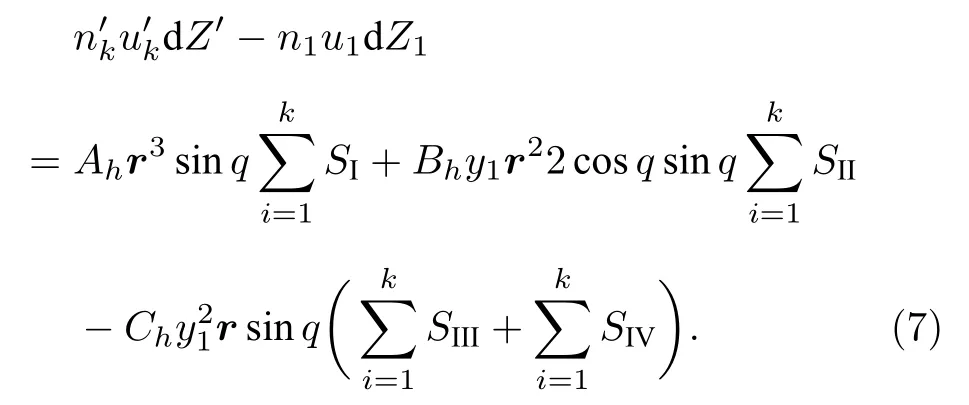
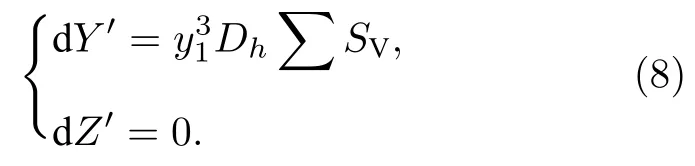
說明主光線經有畸變像差的光學系統折轉后與理想像點偏離量為

在本光學系統中, 自由曲面校正畸變的原理可以概括為: 在傳統目鏡成像的基礎上, 增加自由曲面光學元件, 改變每一個視場的光線的最終出射方向, 使得每個視場的光線都能到達其無視覺畸變所對應的新像點, 從而實現視覺上的畸變校正.自由曲面光學表面相對于非球面而言具有更大的自由度, 在其表面上的每一點都有不同的曲率半徑和法線方向.由于入射光線、出射光線以及自由曲面上的點滿足Snell定律[23], 可以建立起自由曲面上每一點的入射光線、出射光線和自由曲面上點的位置和法線方向之間的關系為

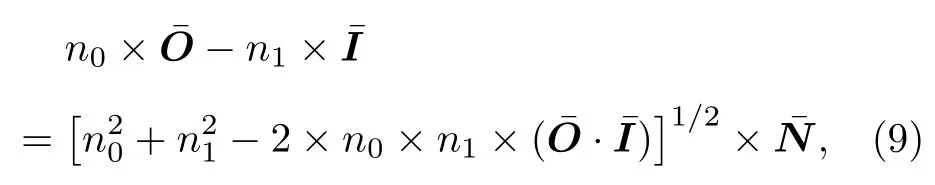
其中 n0為空氣折射率,為出射光線單位矢量, n1為球面與自由曲面之間的介質折射率,為入射光線單位矢量,為自由曲面上點的單位法矢量.

根據(9)式的關系以及前文由像差表達式推導得知的主光線偏離量, 可通過光學設計軟件對系統成像質量進行模擬并且計算畸變大小, 然后針對自由曲面多項式系數進行優化以改變其面形, 從而對各點光線進行逐一校正.所以可以利用自由曲面代替圖像處理的方法來校正成像系統畸變.

將自由曲面運用到顯微目鏡這種大視場、小孔徑的光學系統中, 可以獲得較高的放大倍率以及較小的畸變像差.本設計應用的XY多項式自由曲面是在二次曲面的基礎上增加了最高冪數不大于 p 的多個 xmyn單項式, ( x,y,z) 為自由曲面上點的坐標,其描述方程為[24]

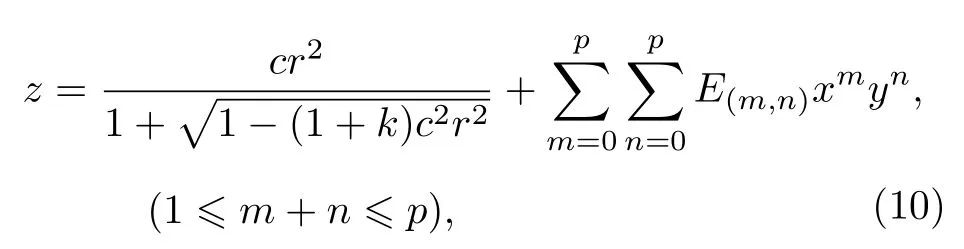
由于將自由曲面應用于同軸系統中, 故將自由曲面設計為關于YOZ與XOZ面對稱.又因為(x,y,z)為自由曲面上點的坐標, 優化單項式xmyn的系數 E(m,n)即可改變自由曲面面形, 從而校正畸變等像差.取 p =8 , 方程為8階XY多項式曲面,系統自由曲面的方程為

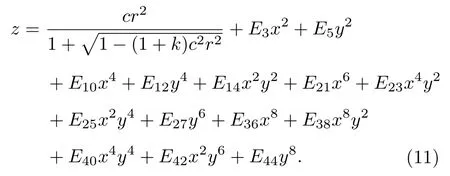
3 仿真設計

大倍率廣角顯微目鏡的參數指標如表1所列.

我們的最終設計是只有四個玻璃鏡片和一個塑料鏡片的組合.基于自由曲面的大倍率廣角顯微目鏡的光學系統結構示意圖如圖3所示, 本系統采用反向光路設計, 故以平行光入射.選擇由兩個膠合透鏡組和一個單正透鏡組成的Erfle廣角目鏡結構作為初始結構, 選擇合適的結構后, 使用不同類型玻璃材料的正確組合對鏡頭進行像差校正, 結合自由曲面進行優化, 即可完成設計過程.

廣角顯微目鏡的光學系統數據與XY多項式自由曲面的面型參數如表2和表3所列.其中第一個元件為光焦度為正的雙膠合透鏡, 第二元件為光焦度為正的單透鏡, 第三元件為光焦度為負的雙膠合透鏡.第一、三元件利用正負光焦度結合來校正系統色差, 減小第二元件與第一、三元件的間距以減小場曲.玻璃材料選自成都光明玻璃庫, 第二元件單透鏡前后兩面都應用了自由曲面, 并選取PMMA這種光學塑料, 因為其便于自由曲面的加工、重量較輕且成本低廉.

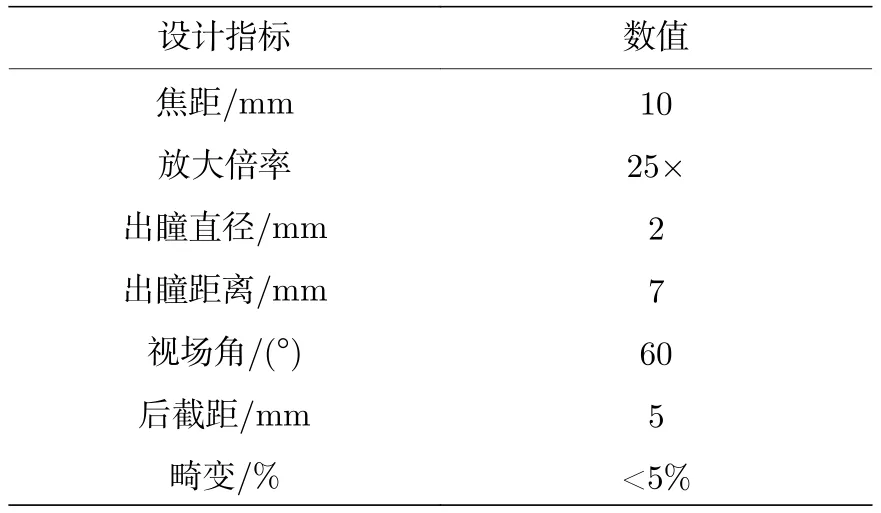
表1 廣角顯微目鏡參數指標Table 1.Design requirements for the wide-angle microscope eyepiece.

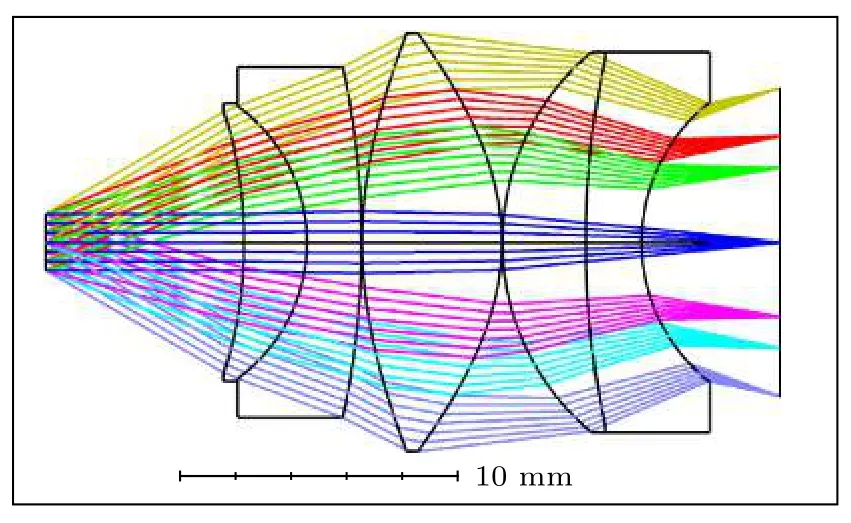
圖3 廣角目鏡光學系統結構圖Fig.3.Structure diagram of wide-angle eyepiece optical system.

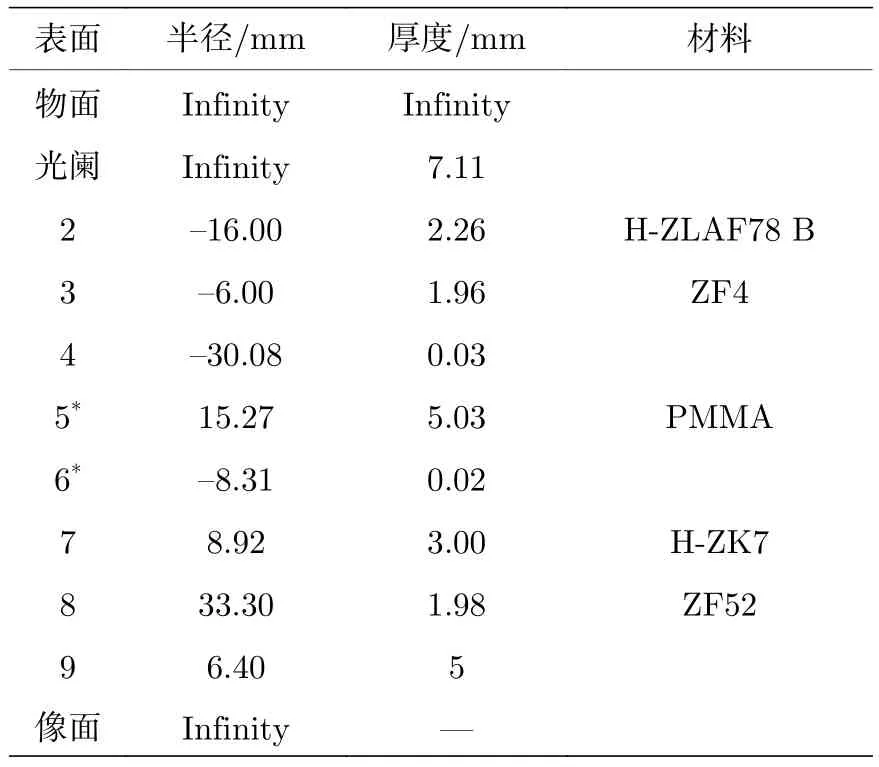
表2 廣角目鏡光學系統參數Table 2.Optical prescription data for wide-angle eyepiece optical system.

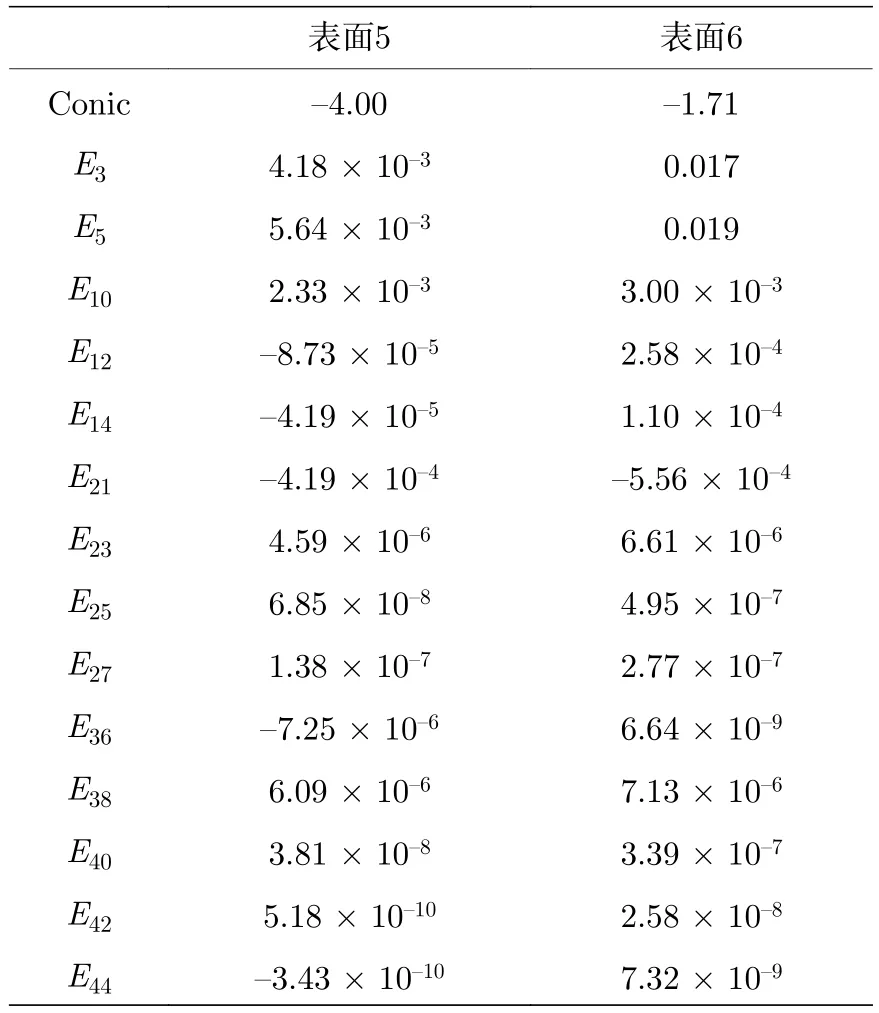
表3 XY 多項式系數Table 3.XY polynomial coefficients.

根據自由曲面描述公式以及各項系數, 用Matlab軟件對第5, 6兩面的自由曲面面型進行擬合, 得到如圖4所示的結果.

傳統的Erfle目鏡通常應用于低倍觀測, 在高倍觀測表現不佳.本設計將傳統結構與自由曲面相結合, 獲得了高放大倍率、大視場且成像質量良好的廣角目鏡系統.

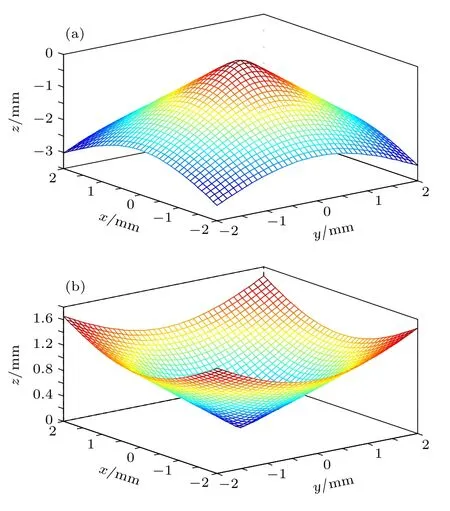
圖4 自由曲面面型擬合示意圖 (a) 第 5 面面型; (b) 第6面面型Fig.4.Simulation of freeform surface shape: (a) Shape of surface 5; (b) shape of surface 6.

4 設計結果分析

廣角顯微目鏡的成像評價指標如表4所列.

圖5顯示了本系統7個視場子午和弧矢方向的調制傳遞函數(MTF)曲線, 在40 lp/mm處所有視場 MTF均大于 0.3, 平均 MTF大于 0.5, 滿足目視系統分辨率要求, 成像質量良好.

畸變定義為主光線與高斯像面的實際交點和理想像高之間的差異, 相對畸變定義為

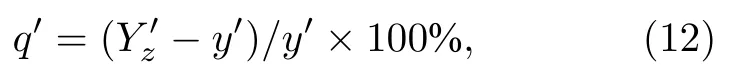
其中 q′代表相對畸變;為主光線與高斯像面相交的實際像高; y′為理想像高.畸變與視場成正相關, 視場越大, 光學系統畸變越嚴重.由于畸變不影響成像清晰度, 故目視系統中允許一定程度的畸變, 如表5所列.

表4 成像質量評價指標Table 4.Evaluation index of imaging quality.

表5 一般目視系統允許的相對畸變[5]Table 5.Distortion allowed by general visual systems.

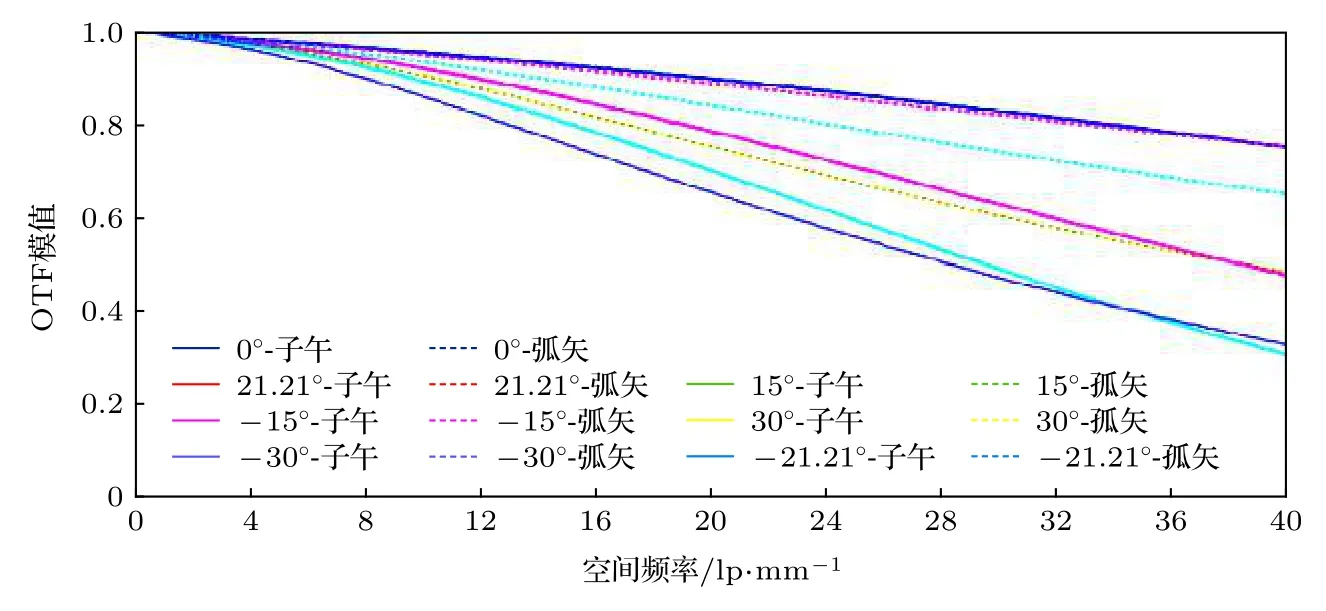
圖5 MTF 曲線圖Fig.5.MTF of microscope eyepiece.

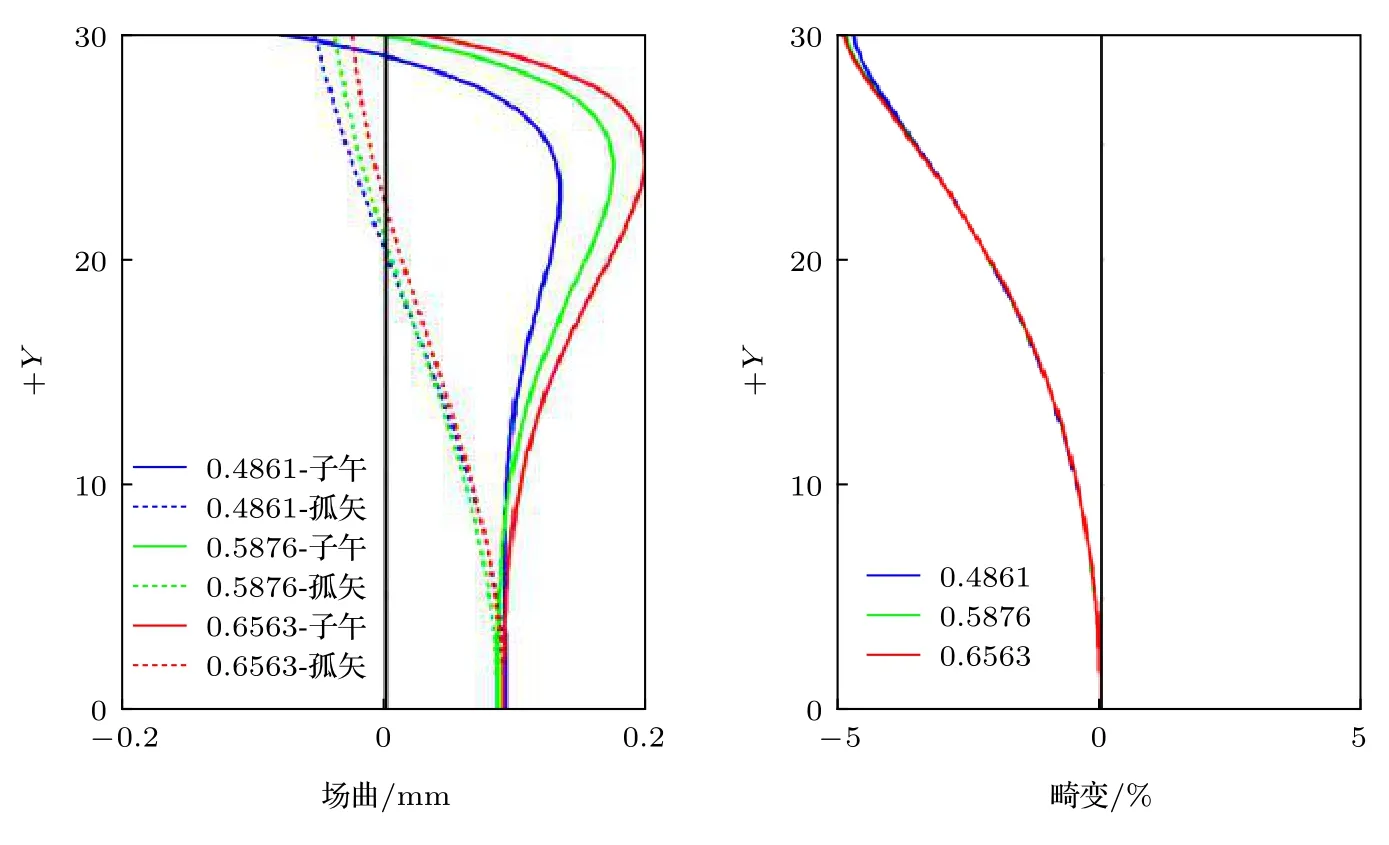
圖6 場曲與畸變Fig.6.Field curvature and distortion.

圖6顯示了本目鏡系統的場曲與畸變.本設計的視場角達到60°, 而相對畸變小于5%, 說明自由曲面對大視場小孔徑光學系統的畸變校正達到了較好的效果.圖7顯示了本光學系統的畸變網格.由于應用在第5和6面的自由曲面關于YOZ與XOZ面對稱, 故產生的畸變也關于這兩面對稱.

圖7 畸變網格Fig.7.Grid distortion.

對系統進行公差分析以確定該系統是否易于加工, 公差值如表6所列.公差分析結果證實了制造符合規格的廣角目鏡的能力.所有公差均在制造和組裝的通常能力范圍內.表7列出了蒙特卡羅分析的結果, 該結果估計了廣角目鏡在制造和組裝后的MTF值.結果表明, 有50%的蒙特卡羅模擬得出的 40 lp/mm 處平均 MTF ≥ 0.523, 這滿足了能接受的標準, 即50%的蒙特卡羅模擬必須大于或等于設計要求的MTF數值.分析結果表明, 該廣角目鏡可以被成功地制造和組裝.

表6 公差系數Table 6.Tolerance Parameter.

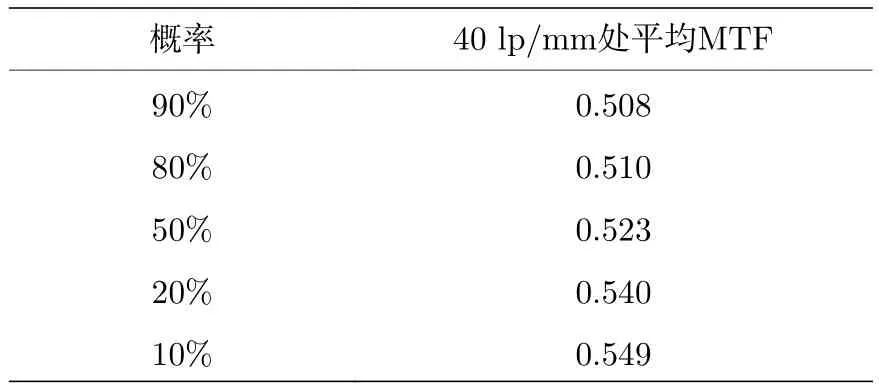
表7 蒙特卡羅分析結果Table 7.Results of Monte Carlo analysis.

5 總 結

本文根據像差理論, 推導了目鏡光學系統的光學特性與像差特點, 對大視場顯微目鏡的設計方法以及自由曲面對大視場畸變的校正原理進行了分析與說明.應用自由曲面設計了一款焦距為10 mm、出瞳直徑 2 mm、視場角 2 ω =60?、出瞳距離為7 mm的高放大倍率廣角顯微目鏡, 并分析了其成像質量與公差.設計結果表明, 該顯微目鏡成像質量良好, 全視場畸變小于5%, 且系統結構簡單易于加工與裝調, 滿足大視場顯微鏡的使用要求.