確定大氣邊界層頂高度的新方法及數值實驗*

周建印 項杰 黃思訓2)?

1) (國防科技大學氣象海洋學院, 南京 211101)

2) (國家海洋局第二海洋研究所, 衛星海洋環境動力學國家重點實驗室, 杭州 310012)

提出了一種確定大氣邊界層頂高度的數值微分新方法, 該方法使用了正則化技術, 把對彎角廓線求導數的數值微分問題轉化為求目標泛函極小值的問題, 采用雙參數模型函數方法來選擇正則化參數, 最后利用最大梯度法確定邊界層頂高度.首先通過兩個數值實驗驗證了新方法的有效性, 實驗結果顯示, 隨著掩星資料噪音的增多, 由差分法和結合L曲線方案的數值微分方法得到的邊界層頂高度波動增大, 而通過雙參數模型函數方法得到的高度很穩定, 這說明新方法能夠很好地過濾噪音, 從而保留廓線的主要信息.隨后基于2007—2011年1, 4, 7, 10月的COSMIC彎角數據, 利用新方法分析了全球海洋大氣邊界層頂高度的季節特征, 并與用掩星資料自帶的大氣邊界層頂高度數據zbalmax得到的季節分布進行對比.結果表明, 兩者的季節分布特征十分一致: 海溫相對周圍海域高的區域, 邊界層頂高度較高, 反之, 邊界層頂高度較低; 在暖流經過的海域, 邊界層頂高度較高, 在寒流經過的海域, 邊界層頂的高度相對較低.

1 引 言

行星邊界層是對流層底層的大氣, 下墊面主要通過熱量輻射傳輸、摩擦阻力、水汽通量、污染物排放以及地形對邊界層發生作用[1].邊界層的結構復雜多變, 邊界層頂高度隨時空變化而變化, 通常定義為混合層(常值通量層)與自由大氣過渡的高度[2], 高度變化范圍在幾百米到幾千米之內.邊界層頂高度在數值預報模式中的邊界層參數化方案以及氣溶膠的反演中有著重要的作用, 具體表現為: 如果邊界層頂高度太低, 則邊界層與云層解耦,從而抑制了熱量、水分和湍流動能從海洋表面到云層的垂直傳輸, 并可能加速云的消散; 如果邊界層頂高度太高, 則會形成積云而不是層狀云[3], 所以確定邊界層頂高度是一項十分重要的工作.

邊界層頂往往存在濕度、溫度、折射率、氣溶膠粒子以及云滴的急劇變化[4], 無線電掩星探測獲得的彎角和折射率廓線在邊界層頂處往往具有大的垂直梯度, 因此, 最大梯度所在的高度被認為是邊界層頂高度[5].在計算邊界層頂高度的觀測數據方面, 由于邊界層頂高度的變化在幾百米左右, 而被動紅外和微波探測的分辨率在1—2 km, 故使用分辨率大約在20 m的掩星資料計算邊界層頂高度更加精確, 而且全球定位系統掩星探測(global positioning system radio occultation, GPS-RO)技術具有全天候、全球覆蓋、長期穩定等優點, 使得在分析全球邊界層頂高度時更具有優勢.

前人在計算邊界層頂高度上, 提出了許多方法.Holzworth[6]通過從最高表面溫度沿干絕熱線隨高度上升到與最近觀測到的溫度廓線的交點, 來得到最大混合層高度; Coulter[7]比較了由激光雷達、聲雷達以及溫度廓線得到的混合層頂高度, 發現激光雷達與聲雷達探測的高度基本一致.Van Pul等[8]由無線電探空資料通過氣塊法(parcel method)得到了邊界層頂高度.在 20 世紀, Bianco和Wilczak[9]基于模糊邏輯方法的混合深度識別算法來確定邊界層深度; Lokoshchenko[10]提出了一種方法, 即把參數積分(如不穩定能量)最大值所在的高度作為混合層高度; Balsley等[11]使用最小風切變和最大Brunt-V?is?l?頻率對夜晚穩定邊界層頂高度進行計算; Sokolovskiy等[12]把COSMIC掩星探測折射率梯度的最大下降點的高度確定為邊界層頂高度, 2007年Sokolovskiy等[13]又利用COSMIC掩星彎角資料對邊界層頂高度進行了計算; Baars等[14]修正了小波協方差方法, 利用雷達資料得出邊界層頂高度; Seidel等[15]用無線電掩星資料比較了計算邊界層頂高度的6個氣象要素(如溫度、濕度、折射率等), 結果顯示折射率和位溫的梯度最小值得出的邊界層頂高度較高;Dai等[16]使用多個外場觀測項目中飛機測量的廓線資料, 重新計算了邊界層頂高度; Yan等[17]把帶有正則化技術的數值微分方法應用于COSMIC掩星彎角資料來確定大氣邊界層頂高度.

正則化技術是蘇聯科學院院士吉洪諾夫(Tikhonov A N)[18]為了獲得線性不適定問題穩定的近似解而于1963年提出的.隨著研究的深入,正則化的方法得到了蓬勃的發展, 目前常見的正則化方法主要有Tikhonov正則化方法[19], Lavrentiev正則化方法[20], 迭代正則化方法(如Tikhonov迭代方法[21]、Landweber迭代方法[22]), 以及基于譜理論的正則化方法(如TSVD (譜截斷)正則化方法[23])等.前人在大氣科學領域中應用正則化方法做了很多有意義的工作[24?28], 而其中正則化方法的一個關鍵環節是正則化參數的選擇, 常用的正則化參數選擇方法有L曲線準則[29?31]、廣義交叉驗證準則[32,33]、Morozov 偏差準則[34]等.其中,Morozov偏差準則是一種應用非常廣泛的后驗選取策略, 但是此原則仍然不夠理想, 于是1984年Morozov[35]提出了吸收的Morozov準則(damped Morozov principle), 它是通過求解吸收的 Morozov偏差方程來得到正則化參數, 但該方法在進行數值求解時, 收斂速度慢且計算量巨大.于是在1998年, Kunisch和Zou[36]提出單參數模型函數法來求正則化參數, 從此模型函數法為減少計算量指出了一條明確的道路.

在Yan 等[17]提出的帶有正則化技術的數值微分中, 正則化參數的選擇采用了L曲線方法(因此, 該方法在下文中簡稱為L曲線方法), 但是此方法計算量大, 且L曲線方法的收斂性問題在理論上并沒有得到解決.因此, 本文提出一種計算大氣邊界層頂高度的新的數值微分方法, 其中仍然應用了正則化技術, 但是正則化參數的選擇采用了雙參數模型函數方法.本文第2節首先介紹了研究所用到的數據, 然后介紹雙參數模型函數方法的原理;第3節進行數值實驗, 并與另外兩種方法的結果作比較, 以驗證方法的合理性; 第4節應用雙參數模型函數方法得到全球海洋邊界層頂高度的季節分布特征, 并與利用掩星資料自帶的邊界層頂高度得到的結果作對比; 第5節是總結.

2 數據與方法

2.1 數 據

FORMOSAT-3/COSMIC是美國與中國臺灣合作的一個GPS掩星探測項目, 本文使用的彎角廓線數據來自COSMIC項目, 包括2007—2011年的 1, 4, 7, 10月份的全球的彎角數據 (https://cdaac-www.cosmic.ucar.edu/cdaac/products.html),總樣本為1074349條廓線, 其中平均每個月的數量在50000—70000條, 4和7月份比1和10月份數量多 30000—40000 條 (圖1); 同時, atmPrf文件本身還自帶了利用彎角數據得到的大氣邊界層頂高度數據zbalmax.考慮到數據不可避免會帶有缺省缺測等不足, 所以從以下兩方面進行質量控制.1)篩選數據.考慮到邊界層頂基本都在500 m以上, 5 km 以下, 所以本文采用這樣的彎角數據,即廓線的最低高度在0.5 km以上, 最高高度在5 km 以下.2)控制數據長度.選擇有效數據的長度至少在5個以上, 以減小由于數據缺少而帶來的誤差.

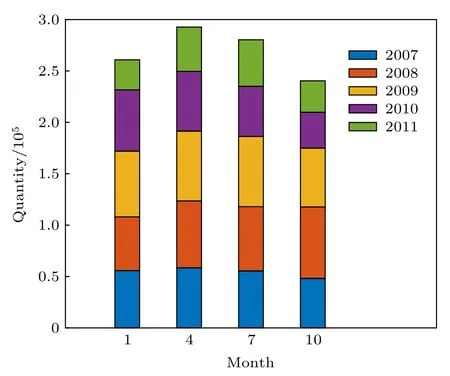
圖1 2007?2011年1, 4, 7, 10月份掩星廓線數量的時間分布Fig.1.Temporal distribution of the number of occultation profiles in January, April, July and October, 2007?2011.

2.2 雙參數模型函數方法

大氣邊界層頂常常會有溫度或水汽壓的急劇變化(溫度急劇上升或水汽含量急劇下降), 因此,可以采用最大梯度法來確定邊界層頂高度.近些年來, 使用“開環”跟蹤技術之后, GPS 掩星資料在低層大氣的準確度有了顯著提高, 使得GPS掩星資料可以提供更多有價值的低對流層(尤其是離地面2 km以下)大氣的信息, 但是由于水汽的影響,低對流層(尤其是離地面2 km以下)大氣廓線數據仍然含有負偏差.Yan 等[17]提出的數值微分方法中, 正則化參數的選擇采用了L曲線法, 由于L曲線法具有前面提到的兩個缺陷, 所以本文采用雙參數模型函數方法來確定彎角梯度.

2.2.1 模型的構建

模型構建的基本思路與Yan 等[17]相同, 為了文中敘述的方便, 下面對模型的構建作簡要介紹.設彎角為連續可微的函數 α (z) , 彎角廓線的梯度為 φ (z)= α′(z) , z 為高度, 范圍為 z0?z?zn.

在高度范圍 I =[z0,zn]中取i=1,2,···,n, 根據牛頓萊布尼茲公式可以得到

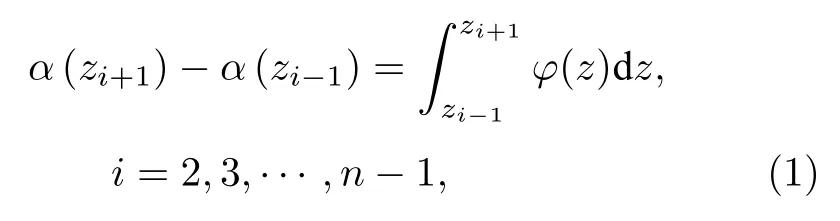
對于(1)式右側, 可以用辛普森法則近似為

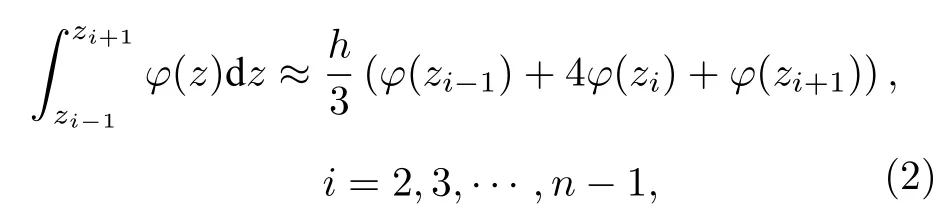
其中, 2h=zi+1?zi?1=2(zn?z0)/n, 本文將廓線等分為 n 份, 每一份高度 h 為 10 m, 誤差為error= ?h5/90φ(4)(ξ),ξ∈ [zi?1,zi+1], 如 果 彎 角梯度變化劇烈, 比如存在鋒面過程等劇烈變化的天氣時, 則誤差不容忽視.

將(2)式代入(1)式可以得到

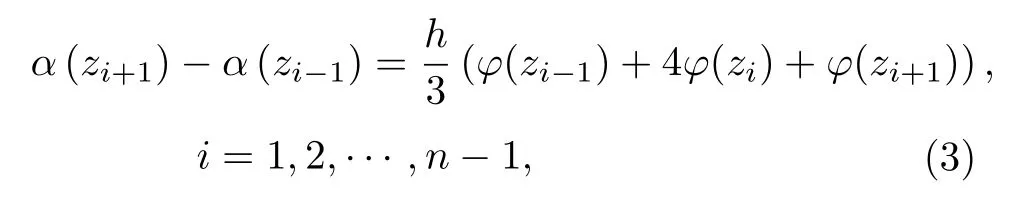
經整理后可得到彎角梯度應滿足的線性方程:

其中

此時, 問題歸結為求線性方程(4)的解.

2.2.2 雙參數模型函數方法的應用

考慮模型(4), 如果觀測資料b帶有高頻成分,則在反演大氣彎角垂直梯度時, 結果會產生較大的誤差.所以, 為了克服 (4) 式的不適定性, 本文把(4)式轉化為求解如下目標泛函極小值的問題:

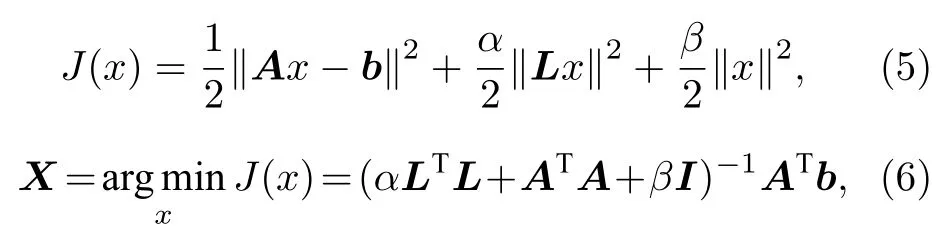
其中X是滿足泛函極小值的解, α ,β 是待求的雙正則化參數, 而矩陣L為一階導數算子, 表示對x進行約束, 使得x的梯度變化不至于過于劇烈,起到平滑的效果.

本文與Yan 等[17]文章中的不同之處是采用雙參數的模型函數方法[36?39]來確定目標泛函中兩個參數的最優解, 進而求解出彎角梯度, 其基本技術路線如下:

令目標函數 F (α,β) 為

此時吸收的Morozov偏差方程為

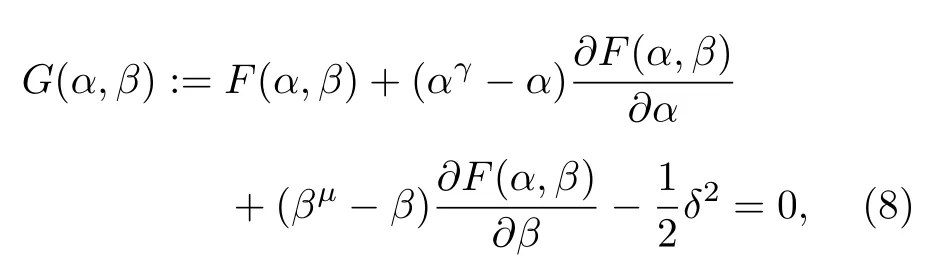
式中 γ >1,μ>1 為吸收系數, δ 為誤差水平.因為(8)式是關于 α ,β 的高度非線性方程, 用通常的迭代方法求解結果并不理想(比如Newton法和擬Newton法), 原因是他們只具有局部收斂的性質,而且對初值的要求比較高.因此, 我們采用近年來得到廣泛應用的模型函數法來確定正則化參數, 模型函數法的好處是不但計算量大大減少, 而且還保證了收斂性.模型函數有各種選擇的方法[38,39], 為簡單起見采用線性模型函數mk(α,β):=Tk+αCk+βDk表示第k次迭代的結果以逼近 F (α,β) , 其中

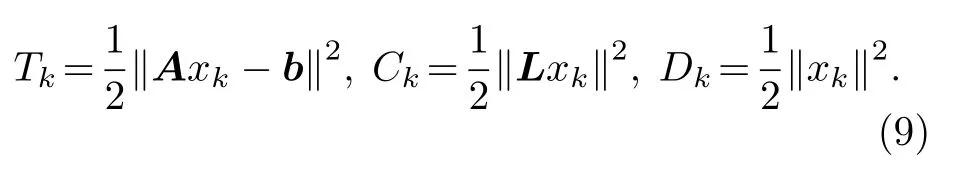
圖2 雙參數模型函數法流程圖Fig.2.Flow chart of two-parameter model function method.

將(9)式代入(8)式可得

確定正則化雙參數的計算流程如圖2所示.因為在正則化方法中物理量往往是無量綱的, 為了使正則化中的量綱一致, 將 α ,β 做了以下處理: 將 α 擴大500×std(b)倍, 將 β 擴大 s td(b) 倍, 這里 std(·) 表示取標準差.

3 數值實驗

本節比較了三種確定邊界層頂高度的方法, 分別是模型函數法、差分法和L曲線方法.所用數據是 2011年1, 4, 7, 10月份的 COSMIC 彎角資料.在處理之前先對數據進行質量控制, 然后借助spline插值法將資料插值到間隔為10 m的網格點上.雙參數模型函數法的兩個初始參數 α ,β 都取為 1, 根據彎角的量級為 10?2, 故取 δ =10?2, 收斂參數 ε =10?4.由差分法、L曲線法以及模型函數法計算出來的邊界層頂高度分別記為 Hd,HL,HM.

掩星探測資料不可避免地會帶有誤差, 為了比較在存在噪聲情況下幾種方法的表現, 本節將[?δ,+δ]上的隨機誤差添加到彎角資料, 由于在邊界層中彎角的量級為 10?2, 故令 δ ∈[0.0001,0.01],在帶有噪聲的彎角資料的基礎上, 通過與差分法和L曲線法相比較, 檢驗模型函數法在確定邊界層頂高度上是否具有準確性.

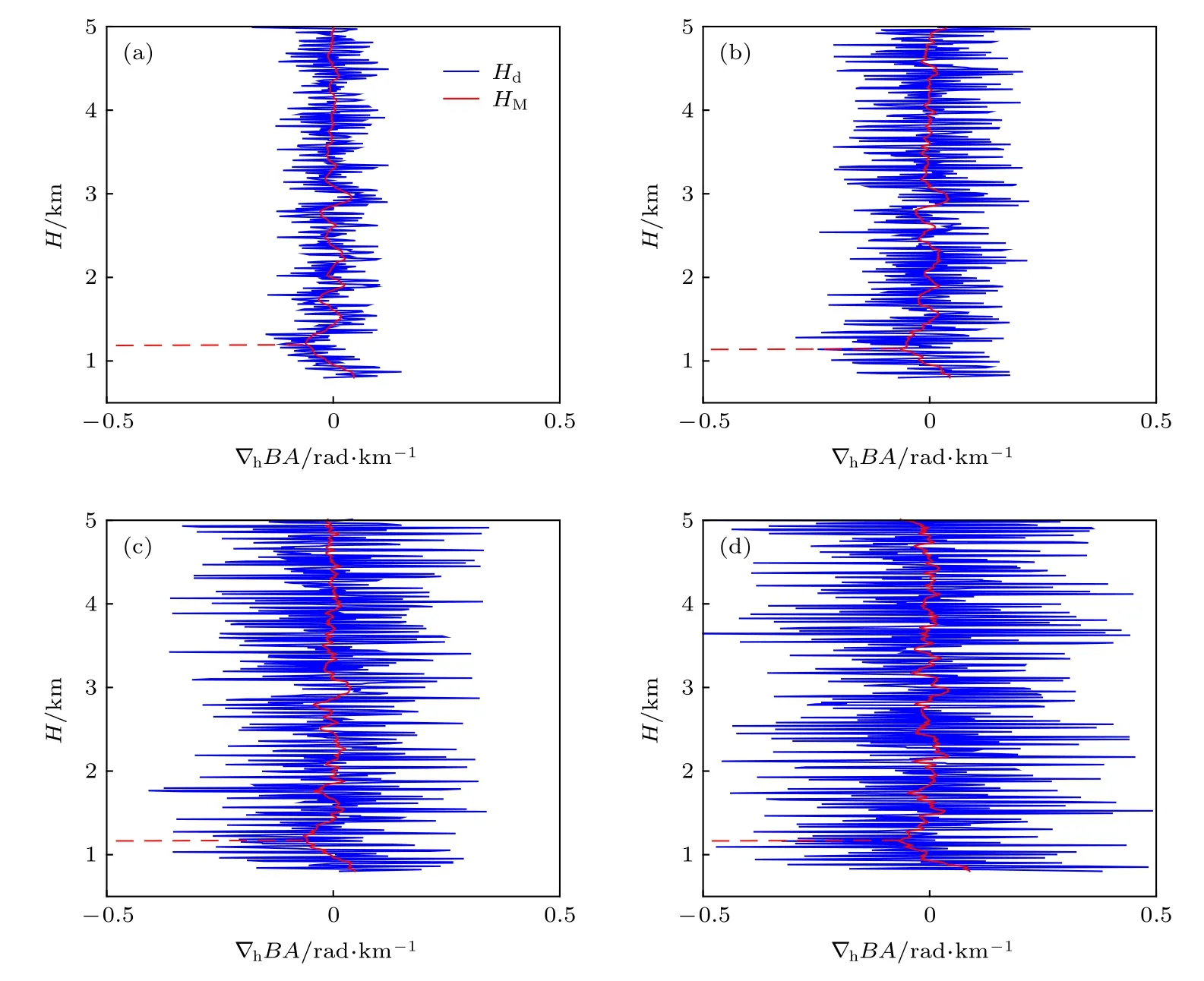
圖3 由差分法和模型函數法得到的彎角梯度廓線(BA表示彎角) (a)彎角廓線添加隨機誤差 δ =0.0025 , 邊界層頂高度HM=1.2km,Hd=1.4km ; (b)彎角廓線添加隨機誤差 δ =0.005 , 邊界層頂高度 HM=1.1km,Hd=1.4km ; (c)彎角廓線添加隨機誤 差 δ =0.0075 , 邊界層 頂高 度 HM=1.2km,Hd=1.8km ; (d)彎角 廓線 添加隨 機誤差 δ =0.01 , 邊界 層頂高度 HM =1.2 km, Hd = 3.7 kmFig.3.Angle gradient profile obtained by the difference method and the model function method using the bending angle gradient profile (BA represents the bending angle): (a) Bending angle profile with uniform random error δ =0.0025 , boundary layer top height HM=1.2km,Hd=1.4km ; (b) bending angle profile with uniform random error δ =0.005 , boundary layer top height HM=1.1km,Hd=1.4km ; (c) bending angle profile with uniform random error δ =0.0075 , boundary layer top height HM=1.2km,Hd=1.8km ; (d) bending angle profile with uniform random error δ =0.01 , boundary layer top height HM=1.2km,Hd=3.7km.

圖3選取了廓線atmPrf_C001.2011.182.05.19.G18_2013.3520_nc, 并且分別添加隨機誤差δ=0.0025,0.005,0.0075,0.01, 比較了差分法和數值微分結合模型函數方法得到的邊界層頂高度.從結果可以看出, 圖3(a)是由帶有誤差 δ =0.0025 的彎角得到的彎角梯度, 差分法得到的彎角梯度廓線在一定水平范圍內呈密集的鋸齒狀, 其最小梯度在1.4 km左右, 數值微分方法結合模型函數法得到的彎角廓線比較光滑, 其最小梯度在1.2 km左右, 由圖3(b)—(d)可知, 隨著彎角資料誤差的增大, HM始終穩定在 1.2 km 左右, 而 Hd由 1.4 km(圖3(a)和圖3(b))變為 3.7 km(圖3(d)), 變化幅度超過2 km, 說明當掩星資料中存在觀測誤差時,模型函數法能夠很好地過濾噪聲, 保留主要信息,得到的邊界層頂高度的結果更加穩定.

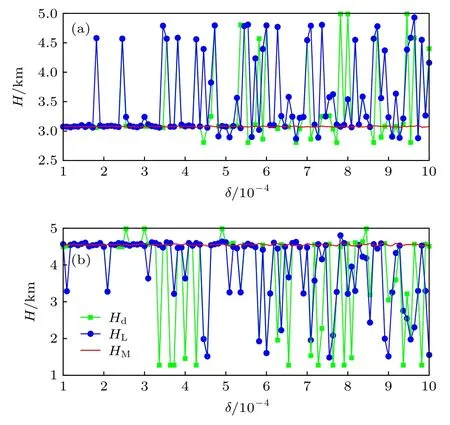
圖4 由差分法、L曲線法和模型函數法得到的邊界層頂高度 (a) 三種方法基于廓線1得到的邊界層頂高度, Htrue =3.15 km, std(HM) = 0.013, std(HL) = 0.44, std(HM) = 0.61;(b) 三種方法基于廓線2 得到的邊界層頂高度, Htrue = 4.55 km,std(HM) = 0.020, std(HL) = 0.89, std(HM) = 1.19Fig.4.Height of the boundary layer obtained by the three methods: (a) Three methods to get the height of the boundary layer top based on profile 1, Htrue = 3.15 km, std(HM) =0.013, std(HL) = 0.44, std(HM) = 0.61; (b) three methods to get the height of the boundary layer top based on profile 2,Htrue = 4.55 km, std(HM) = 0.020, std(HL) = 0.89, std(HM) =1.19.

圖4給出了三種方法(模型函數法、差分法、L曲線法)分別在兩條添加誤差后的彎角廓線(atmprf_C001.2001.182.00.22.G23_2013.3520_n c, atmPrf_C001.2011.182.00.39.G20_2013.3520_nc)上的表現, 以結果的標準差衡量方法的穩定度.由圖4(a)可以看出, HM比較穩定, 保持在 3.15 km左右, 而 Hd和 HL隨著誤差的增大, 波動越來越大,其中, HM,Hd,HL的穩定度分別為 0.013, 0.44 和0.61; 同樣由圖4(b) 也可以看出, HM依然是比較穩定, 保持在 4.55 km 左右, 而 Hd和 HL隨著誤差的增大, 波動也越來越大, 其中 HM,Hd,HL的穩定度分別為0.02, 0.89和1.19.由以上分析可以看出,彎角資料的噪聲越大, Hd振蕩程度就越強, HL振蕩的程度次之, 而 HM的穩定性則比較好, 說明對于含有噪聲的彎角資料, 模型函數法也能穩定地得到邊界層頂高度, 所以模型函數法在確定邊界層頂高度時, 準確性能得到保證.

4 全球邊界層頂高度的季節特征

本節應用模型函數法, 對海洋上邊界層頂高度的季節特征進行分析.圖5展示了2007—2011年的 1, 4, 7, 10 四個月份年平均的邊界層頂高度, 可以看出, 1月份南半球的邊界層頂達到最高, 尤其是中高緯度海洋上的邊界層頂高度達到2 km以上;4月份南半球的邊界層頂高度開始降低, 南美洲與南極大陸南設得蘭群島之間的德雷克海峽附近降低的程度最為明顯, 而北極附近海域的邊界層頂高度也降低, 原因在于北極的海冰覆蓋面積在3月份達到高峰, 4月份海冰的面積比1月份多[40], 所以4月份下墊面溫度更低, 相應的邊界層頂高度也在4月份比1月份低; 七月份南半球中高緯度的邊界層頂高度在四個月份中最低, 北半球的低緯度地區邊界層頂高度明顯增高, 如墨西哥灣地區、阿拉伯地區以及日本海地區, 而受西太平洋副熱帶高壓下沉氣流影響, 我國東南沿海、孟加拉灣和菲律賓附近海域邊界層頂高度明顯降低; 10月份南半球中高緯邊界層頂高度略有回升, 北極海域邊界層頂高度開始降低, 而此時我國東南沿海、孟加拉灣和菲律賓附近海域邊界層頂高度明顯升高.

從以上現象分析可以得知, 隨著太陽直射點的南北移動, 海洋上的邊界層頂高度呈現明顯的季節變化特征, 邊界層頂高度與海面的溫度密切相關,當海面的溫度相對周圍平均溫度越低時, 邊界層頂高度越低, 反之, 邊界層頂高度就越高.但是四個月份共同的特征是, 在寒流流經的區域, 邊界層頂高度普遍偏低, 比如巴西寒流和加利福尼亞寒流,暖流流經的區域邊界層頂普遍較高, 比如赤道暖流.圖6展示了利用掩星自帶的zbalmax的資料求得的邊界層頂高度的季節分布, 通過與圖5相比較, 可以看出模型函數法得到的邊界層頂高度略高, 但兩者邊界層頂高度的時空分布十分一致, 說明模型函數法得到的季節特征具有準確性.

圖5 用模型函數法得到的海洋5年平均的邊界層頂高度(所用資料為2007—2011年1, 4, 7, 10四個月份的掩星彎角的資料)(a) 1月份平均邊界層頂高度; (b) 4月份平均邊界層頂高度; (c) 7月份平均邊界層頂高度; (d) 10月份平均邊界層頂高度Fig.5.The 5-year average boundary layer height of the ocean obtained by the model function method, the data used is the bending angle profile of the four months of 2007?2011 in January, April, July, and October: (a) The average height of the boundary layer in January; (b) the average height of the boundary layer in April; (c) the average height of the boundary layer in July; (d) the average height of the boundary layer in October.

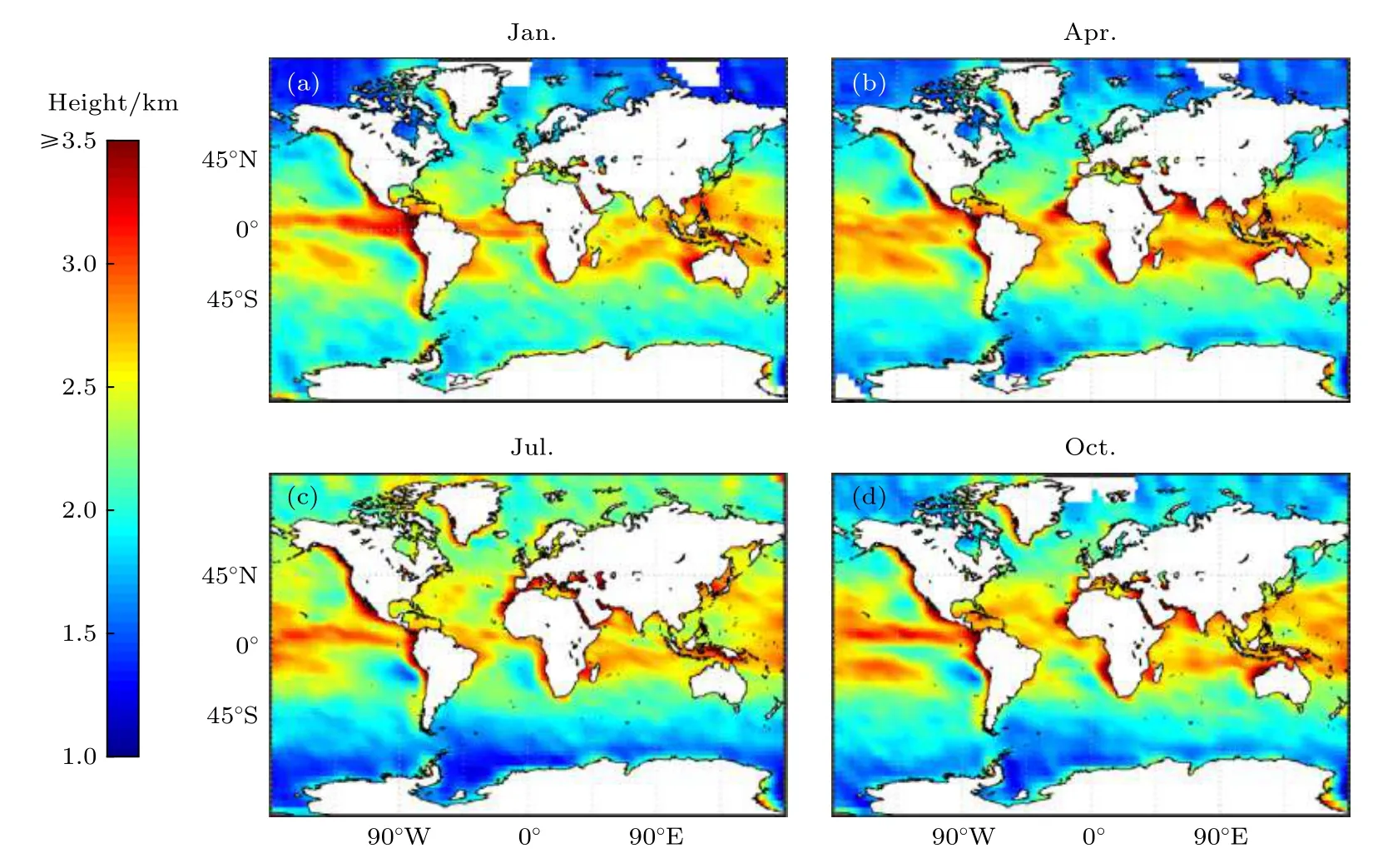
圖6 海洋 5年平均的邊界層頂高度 (所用資料為 2007—2011年1, 4, 7, 10 四個月份的掩星自帶 zbalmax 的資料) (a) 1月份平均邊界層頂高度; (b) 4月份平均邊界層頂高度; (c) 7月份平均邊界層頂高度; (d) 10月份平均邊界層頂高度Fig.6.The 5-year average boundary layer height of the ocean obtained by the model function method, the data used is the zbalmax provided by CDAAC of the four months of 2007?2011 in January, April, July, and October: (a) The average height of the boundary layer in January; (b) the average height of the boundary layer in April; (c) the average height of the boundary layer in July; (d) the average height of the boundary layer in October.

5 總 結

本文提出了一種確定邊界層頂高度的新的數值微分方法, 通過模型函數法確定正則化項中的雙參數, 從而得到彎角梯度, 進而利用最大梯度法確定邊界層頂高度.文中展示了兩個數值實驗的結果, 從中可知, 此方法最主要的優點在于, 盡管掩星資料中帶有誤差, 但其基本不受噪聲的影響, 能夠很好地提取主要的信息, 具有很好的穩定性和準確性.

應用本文提出的方法, 基于2007—2011年的COSMIC掩星彎角資料, 研究了全球海洋邊界層頂高度的季節變化特征, 著重分析了 1, 4, 7, 10 四個月份的年平均邊界層頂高度, 結果顯示, 隨著太陽直射點的南北移動, 海洋上的邊界層頂高度具有明顯的季節變化特征, 其與海溫密切相關, 具體來說, 相對于周圍海域的海溫越低, 邊界層頂高度越低, 反之, 邊界層頂高度越高, 延伸這一結論可以得到, 冷洋流對應著低邊界層頂, 暖洋流對應著高邊界層頂.為了驗證結論的準確性, 將其與利用掩星資料自帶的zbalmax得出來的邊界層頂高度的季節特征作對比, 結果發現, 兩者邊界層頂高度的時空分布特征十分一致, 說明通過雙參數模型函數法得到的季節特征具有準確性.

總之, 經過數值實驗中與差分法和L曲線法的比較, 發現雙參數模型函數法在求邊界層頂高度時具有不可替代的優勢, 而且經過掩星資料自帶的邊界層頂高度數據zbalmax的驗證, 表明文中表述的海上邊界層頂高度的季節特征具有準確性.我們下一步需要繼續做的工作是進一步改進方法, 使其適用于復雜天氣條件下的大氣波導的研究, 以期得到更好的結果.

本文利用的數據來自CDAAC提供的GPS掩星資料,在此謹表感謝! 感謝國防科技大學氣象海洋學院周則明教授對文章行文結構的建議, 感謝國防科技大學氣象海洋學院杜華棟副教授和閆申博士在編程方面的幫助, 感謝國防科技大學氣象海洋學院陳毓敏、徐海波和北京師范大學地理學院孫銘揚對文章提供的修改建議.