開區間內連續函數最值問題的探討
黃明秋
(長沙航空職業技術學院,湖南 長沙 410124)
我們知道,閉區間[a,b]上的連續函數f(x)一定存在最大值與最小值,并且函數在閉區間[a,b]上的最大值與最小值只能在區間(a,b)內的駐點處、不可導點處,以及在區間的端點處取得。因此,求閉區間[a,b]上的連續函數f(x)的最值,只需求出以上3種點處(存在的話)的函數值,然后比較這些函數值的大小,即可得出函數的最大值與最小值。
同時,我們也知道開區間(a,b)內的連續函數f(x)不一定存在最大值與最小值。那么如何比較全面地解決開區間(a,b)內的連續函數f(x)的最值問題呢?
1 下面分以下三種情形進行討論:
1.1 對于有限開區間(a,b)內的連續函數f(x),如果
那么,可以當成求閉區間[a,b]上的連續函數f(x)的最值。
同時,上述方法對于函數f(x)在區間[a,b)、 (a,b]、(-∞,b)、(a,+∞)、(-∞,b]、[a,+∞),(-∞,+∞)連續的最值問題可以按照下面的方式解決。
最后,應當注意確定有沒有最大值與最小值時,只有當所取最值點是在區間(a,b)或(-∞,b)、(a,+∞)、(-∞,+∞)內的駐點處、不可導點處,以及在區間的端點(半開半閉)處時才存在。也就是說如果某最值點取在所設的極限值所對應的點(虛擬點)處時,該最值是不存在的。
例1求函數y=f(x)=sinx-xcosx在區間(0,4π)內的最值。
解y′=cosx-cosx+xsinx=xsinx
求出駐點x=π,2π,3π
又f(x)=π,f(2π)=-2π,f(3π)=3π
所以該函數只有最小值-2π,沒有最大值。
例2求函數y=x2e-x在[0,+∞]內最值。
解y′=2xe-x-x2e-x,求出駐點x=0,x=2
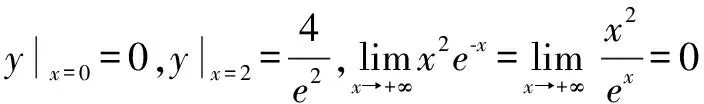
注意本函數只有一個最小值點x=0。
例3求函數f(x)=xe-x2的最值。
解該函數的定義域為(-∞,+∞)
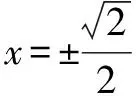

1.2 對于有限開區間(a,b)內的連續函數f(x),如果兩個極限中至少有一個為不存在,且該不存在為+∞或-∞
(1)當某極限為+∞時,則說明該函數一定不存在最大值;
(2)當某極限為-∞時,則說明該函數一定不存在最小值;
(3)當兩個不存在的極限分別為+∞和-∞時,則說明該函數既不存在最大值,也不存在最小值。
注意:(1)極限存在時的處理同第一種情形。
(2)上述方法對于函數f(x)在區間[a,b)、 (a,b]、(-∞,b)、(a,+∞)、(-∞,b]、[a,+∞)、(-∞,+∞)連續的最值問題可以按照第一種情形方式處理。
例4求函數y=x3-3x2-9x+2在(-2,+∞)內最值。
解y′=3x2-6x-9,求出駐點x=-1,x=3
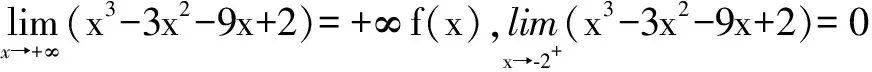
所以,該函數在x=3處取得最小值-25,但該函數不存在最大值。
1.3 對于有限開區間(a,b)內的連續函數f(x),如果兩個極限中至少有一個為不存在,且該不存在既不為+∞,也不為-∞。但存在無限趨近于它的兩個子列和使得兩個子列的極限一個為+∞,另一個為-∞。那么該函數一定既不存在最大值,也不存在最小值
注意:(1)此時,無需再考察端點與駐點、不可導點的情況。
(2)上述方法對于函數f(x)在區間[a,b)、 (a,b]、(-∞,b)、(a,+∞)、(-∞,b]、[a,+∞)、(-∞,+∞)連續的最值問題可以按照第一種情形方式處理。
例5求函數f(x)=cosx+xsinx在[0,+∞)上的最值。
解取無限趨近于+∞兩個子列
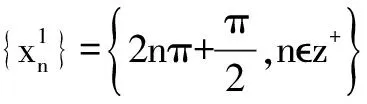
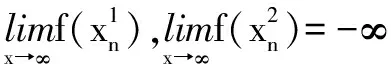
所以,該函數不存在最值。
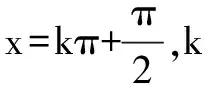
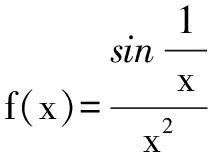
解取無限趨近于0+兩個子列
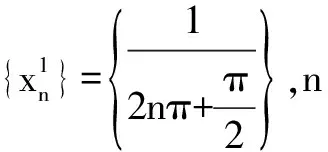
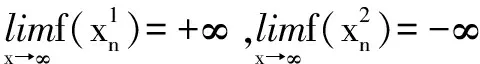
所以,該函數不存在最值。
2 總結
綜合上面的討論,連續函數的最值問題得到了比較全面的解決。

