具有非線性發生率及隔離措施的隨機SIQRS傳染病模型的研究*
陽開榮韋煜明
(廣西師范大學 數學與統計學院,廣西 桂林 541006)
0 引言
近年來,由于各種傳染病的出現給人類的健康帶來了巨大的傷害與損失,而從傳染病動力學的角度研究傳染病的傳播因素為傳染病預防與控制帶來了一定程度的幫助.在以往的一些動力學模型中通常考慮的是確定型的模型,但在實際生活中,傳染病的流行在一定程度上會受到各種不確定因素的影響,比如環境噪聲,很多學者在研究傳染病時也考慮到這個因素.[1-6]文獻[6]中,蔡等人考慮了干預策略下具有傳染性的隨機SIRS傳染病模型
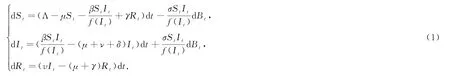
文獻[6]中作者運用了Markov半群理論討論了傳染病的持久性與滅絕性,并得出白噪聲會影響傳染病的爆發.
受文獻[6]的啟發,以及考慮到環境噪聲因素和人為干預隔離措施,本文考慮以下具有非線性發生率及隔離措施的隨機SIQRS傳染病模型
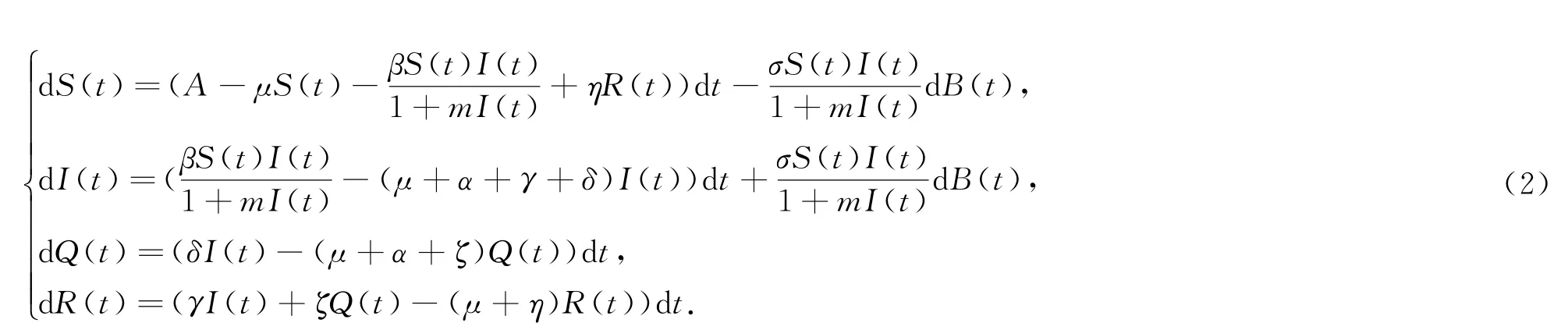
其中S(t),I(t),Q(t),R(t)分別表示易感者、染病者、隔離者及恢復者在時刻t的人口數量.A為易感人口輸入率,μ表示個體自然死亡率,α表示個體因病死亡率,β為接觸率,η為恢復者失去免疫力后再次成為易感者的概率,γ和ζ分別為染病者和隔離者的恢復率,δ為隔離率,B(t)為標準布朗運動,σ2表示白噪聲強度.
1 全局正解存在唯一性
令(Ω,F,(F)t≥0,P)為滿足(F)t≥0單調遞增右連續,且F0包含所有零測集的完備概率空間.我們定義以下正不變集
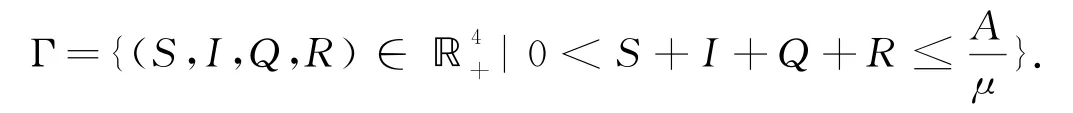
定理1對于任意給定的初值(S(0),I(0),Q(0),R(0)),系統(2)存在唯一的正解(S(t),I(t),Q(t),R(t)),并且該解以概率1屬于?4+,即


2 疾病的滅絕性與持久性分析
2.1 疾病的滅絕


2.2 疾病的持久




例3 對于初值(S(t),I(t),Q(t),R(t))=(0.9,0.1,0,0)取以下參數本文研究了具有非線性發生率及隔離措施的隨機SIQRS傳染病模型,證明了系統(2)全局正解的存在唯一性,給出了疾病滅絕與持久的條件.通過理論分析與數值模擬證明了環境噪聲與人為隔離措施對疾病有抑制作用,因此,我們可以通過增加噪聲的強度以及進行隔離措施來抑制疾病的爆發.
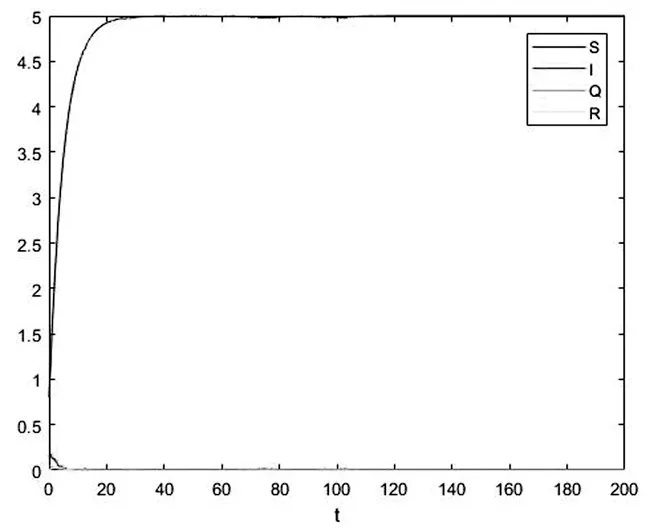
圖1 系統(2)(S(t),I(t),Q(t),R(t))的軌跡圖Fig.1(S(t),I(t),Q(t),R(t))trackdiagramofsystem(2)
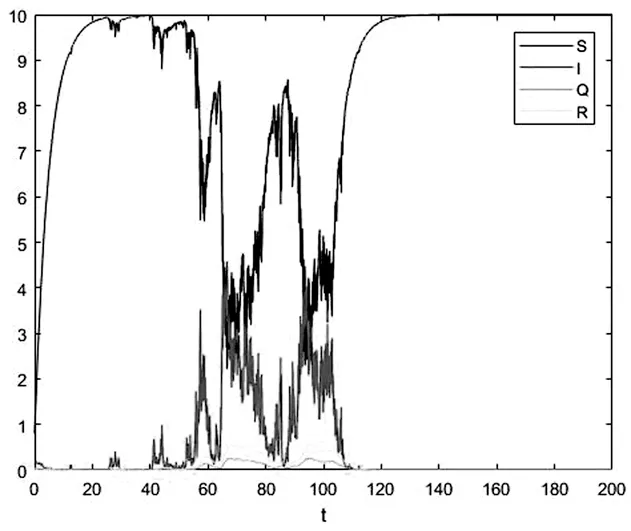
圖2 系統(2)(S(t),I(t),Q(t),R(t))的軌跡圖Fig.2(S(t),I(t),Q(t),R(t))trackdiagramofsystem(2)
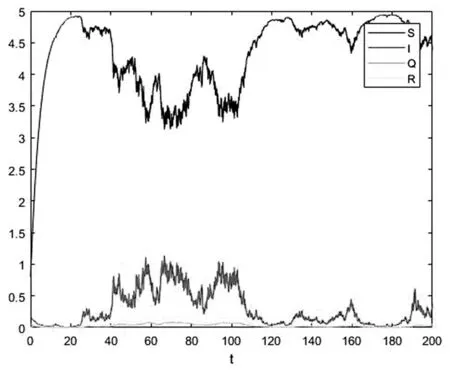
圖3 系統(2)(S(t),I(t),Q(t),R(t))的軌跡圖Fig.3(S(t),I(t),Q(t),R(t))rackdiagramofsystem(2)

