物理解題中的整體意識和局部意識*

張性海

(廣州大學附屬中學 廣東 廣州 510000)

在許多物理問題中，整體與局部的關系是普遍存在的.辯證唯物主義認為, 整體與局部是一對辯證的統一體，整體是指事物的全體或事物發展變化的全過程, 而局部則是指構成事物整體的各個部分及其發展過程的各個階段，整體的特性是由各個局部及其它們的相互作用方式決定的, 局部總會以一定的形式或在一定程度上反映整體的性質.這些辯證關系為教學中處理物理問題提供了一個重要的啟示, 即在解決物理問題時,應當善于從局部去認識整體, 從整體去認識局部，在思維上要訓練學生處理問題的整體意識和局部意識，落實物理核心素養中科學思維能力的培養.筆者結合多年的教學實踐, 談一談在教學中如何用整體意識和局部意識處理物理問題.

1 局部到整體的意識

既然局部是整體的局部, 它總會以某種方式為我們提供關于整體特性的某些信息.當事物從整體上看比較陌生, 而對它分解后的各個局部比較熟悉時, 我們可以從某一局部入手進行研究, 然后將這一局部的認識推廣到另一相似的局部, 直至獲得對事物整體的認識.

【例1】如圖1所示，兩足夠長的光滑平行金屬導軌傾斜放置，導軌左端接有耐壓足夠的電容器C，勻強磁場B垂直導軌平面，有一導體棒垂直導軌和磁場放置，可緊貼導軌自由滑動，導體棒和導軌電阻忽略不計.現導體棒由靜止釋放，電容器兩端電壓為U，導體棒加速度為a,試計算經過時間t時導體棒的速度大小v.

圖1 例1題圖

解析:本題要計算經過時間t時導體棒的速度v，就要判斷導體棒是否做勻加速運動，但是導體棒的運動性質不明，如果全過程(整體意識)入手去處理，無法用現有的運動學公式計算v，為了使研究問題簡化，可以在運動的完整過程中選一段微過程(局部意識)對應的時間Δt來研究.因為Δt很小，故可以認為在Δt時間內導體棒的加速度不變，對導體棒則有

Δε=BLΔv=BLaΔt

且電容器兩極板之間的電壓U和導體棒兩端的電壓相等，故

ΔU=Δε=BLΔv=BLaΔt

且回路中的電流

導體棒受到的安培力

F=BIL=CB2L2a

由

mgsinθ-F=ma

即

mgsinθ-CB2L2a=ma

可得

由a的表達式可見，a是常數，這表明導體棒是做勻加速直線運動，所以，經過時間t時的速度

小結:通過對導體棒某個微過程(局部意識)的分析，進而得出導體棒全過程的運動(整體意識)情況，窺一斑而見全豹，從整體和局部的關系出發，由局部去反映整體的解題思路.用局部意識分析問題時，要注意選取的“局部”具有“任意性”而非“特定性”，像本題中的Δt就是導體棒運動過程中的任一微時間段.

2 從整體到局部的意識

有不少問題, 雖然目標是探求某個局部的狀態, 但若從局部入手, 會受到許多細節的干擾, 或容易使我們陷入片面性和局限性, “ 只見樹木, 不見森林”.此時, 若改變角度, 從整體著眼, 居高臨下, 由整體看局部, 則往往能看到各局部的地位作用及各局部之間的相互聯系,由此對局部建立起正確、清晰的認識.

【例2】如圖2所示，在水平地面正上方有范圍足夠大的勻強磁場.已知磁場的磁感應強度為B，方向水平并垂直紙面向里.一質量為m，電荷量為 -q的帶電微粒從P點開始在此區域做速度為v的勻速圓周運動.初速度v與水平方向夾角為θ=45°,如圖2所示,則為保證該微粒能做完整的圓周運動，P點的高度H應滿足什么條件？(帶電微粒的重力和空氣阻力忽略不計)

圖2 例2題圖

解析:帶電粒子在有界磁場中運動是一種常見的題型，也是學生普遍感覺到難度比較大的題型，究其原因，是因為他們很難畫出粒子在有界磁場中的運動軌跡，也就無法進行相關問題的處理.如果換一個角度思考問題，在題設條件不變的情況下，把畫帶電粒子在有界磁場(局部意識)中運動軌跡(圓的一部分)，換為畫帶電粒子在無界磁場(整體意識)中運動軌跡(完整的圓)，然后再分析粒子在有界磁場中的運動情況，解題思路豁然開朗，難點迎刃而解，有一種柳暗花明又一村的感覺.如圖3所示，給出了帶電粒子在無界磁場中的運動軌跡，根據題設條件，在粒子軌跡圖中標出P點的位置及速度v，如圖4所示，根據題目要求可知，當邊界(地面)在CD位置時，粒子剛好可以做完整的圓周運動，邊界在CD下方時也可以做完整的圓周運動，在CD上方則不行.畫出有界磁場的邊界(地面)CD和P點到地面的最小高度H，根據

和

H=R+Rcosθ

可得

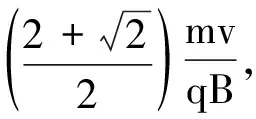
圖3 帶電粒子在無界磁場中的運動軌跡

圖4 粒子軌跡圖中P點的位置及速度

小結:用整體意識處理問題，看問題時“站得高、望得遠”，對問題的把握較為全面和完整.經常能從解題“困境”中打開思路，這種方法要求解題者對問題情景的全面性和狀態的整體性有較好的理解和把握.

3 整體意識和局部意識的對立統一 有利于學生綜合能力的培養

在許多問題處理的過程中，整體意識和局部意識的思路常常交替進行，不同的思路選用不同的方法，方法是解決問題的手段，方法的選擇就是用整體意識和局部意識對問題的判斷，而問題處理的過程就是學生能力培養和發展的過程.

【例3】如圖5所示，傾角為θ，質量為M的斜面體靜止在光滑水平面上.現有質量為m的物塊，以初速度v0從斜面上某處沿斜面減速下滑.已知物塊與斜面體間的動摩擦因數為μ，則在此過程中( )

A.斜面體向左加速運動

B.斜面體對物塊做負功

C.地面給斜面體的支持力等于(m+M)g

D.物塊和斜面體構成的系統水平方向動量守恒

圖5 例3題圖

解析:動量守恒問題涉及的是系統問題，是整體的問題，用整體意識處理，把m和M當作一個整體看待，整體水平方向合外力為零，則動量守恒，選項D正確.斜面體對物塊做功的問題，研究對象是物塊，可嘗試先用局部意識的思路處理，對物塊考慮動能定理

WG+WF=ΔEk

可知斜面體對物塊做的功WF是負值，選項B正確.用整體意識的思路考慮m和M反而對選項B的正確與否較難判斷.對選項A和C，如果用局部意識的解題思路，則對M的受力處理較為繁雜且費時，而把m和M看作一整體，用整體意識的思路考慮問題就簡單很多.對m和M，水平方向由牛頓第二定律得

F合=0=max1+Max2

ax1水平向左，則M的加速度ax2水平向右，M向右做加速運動，選項A錯誤.對m和M，豎直方向由牛頓第二定律得

F合=N-(mg+Mg)=may1+May2

且ay1>0,ay2=0，則N>mg+Mg，選項C錯誤.

小結:是用整體意識還是局部意識的解題思路處理問題，需要嘗試和判斷，在嘗試和判斷中尋求最佳的解題方法，而且兩種解題思路常常交替使用，互為條件，互為結果.

4 總結

學生在分析和解決問題時, 由于認知水平的限制，往往只注重物體或物理過程的局部, 而忽略整體與局部相互依存, 相互作用的關系, 不能從整體著眼、從全局去思考問題.有時則過于關注物體或物理過程的整體，而忽略從局部打開解題突破口的方法，面對題目，往往束手無策.教師在教學過程中要做個有心人, 在知識傳授中，抓住契機對學生加以引導, 對整體與局部的關系進行歸納和總結, 讓其成為學生思考和解決問題的一種習慣, 最終使學生分析和解決問題的能力得到提高.