基于Mathematica的均勻帶電細圓環電場模擬*

高 峰 呂 剛 韓 岳 曹學成 姜貴君 趙文麗

(山東農業大學信息科學與工程學院 山東 泰安 271018)

1 引言

均勻帶電細圓環是大學物理電磁學中一個典型的物理模型．在一般的教材[1]中只計算圓環軸線上的電場強度和電勢分布，鮮少討論該帶電體系在全空間中的電場和電勢．因此，學生很難對該體系在全空間的電場和電勢分布有整體的認識．對于這個問題，有人已經進行了一些研究．文獻[2]和[3]分別在直角坐標系和柱坐標系中導出電勢和電場強度的級數解；文獻[4]使用直接積分的方法分別把電場強度表示為橢圓積分和勒讓德多項式．但這些計算結果僅僅以數學表達式的形式給出，學生很難從公式中把握電場的特點．文獻[5]用數值積分的方法計算橢圓積分, 求出圓環平面上的場強與電勢，討論的范圍仍然不夠完整．文獻[6]利用 Matlab數值計算功能對均勻帶電細圓環在空間激發的電場進行了討論，做出了過環心與圓環垂直的平面內的等勢線和三維空間的等勢面，形象地給出圓環周圍電場的空間分布．但該文獻討論問題略顯單薄，與課堂教學結合仍需拓展．

Mathematica軟件是由沃爾夫勒姆研究公司(Wolfram Research Inc.)研發的一款數值計算和可視化軟件，可以解決各種領域復雜的符號計算和數值計算的問題，也可以方便地畫出各類圖形，從而形象地表示出函數的某些特性，是目前為止使用最廣泛的數學軟件之一．本文利用這一款計算軟件對均勻帶電細圓環在空間激發的電場進行了計算，實現了電場和電勢的可視化，形象展示了該體系靜電場的空間分布，為學生全面掌握這一模型提供了極大的幫助．

2 理論模型與處理

如圖1所示，半徑為a的均勻帶電細圓環，帶電荷量為q，以圓心為坐標原點建立直角坐標系，x軸與y軸在圓環面上，z軸與環面垂直．假設在空間中取一場點P(x,y,z)，則應用點電荷的電勢計算公式，在帶電細圓環上取線元dl，dl所在半徑與x軸的夾角為θ，帶電荷量為

則該電荷元在P點的電勢

dU(x,y,z)=

則整個帶電細圓環在P點的電勢

其中

ε0=8.85×10-12C·N-1·m-2

為真空電容率，為了便于計算，我們取

q=2π×4πε0a=1 m

則上式化簡為

根據電場強度和電勢之間的關系E=-U，可以得到空間的電場強度分布．

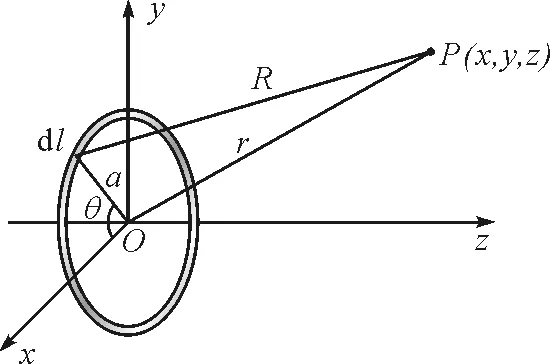
圖1 均勻帶電細圓環

上述理論處理過程并不難理解，但是關鍵的問題是電勢的積分無法用初等函數表示，對電勢求梯度更是一項復雜的工作．如果將上述復雜的積分計算工作交給Mathematica處理，問題就變得簡單多了．

3 電場強度和電勢的計算及可視化

3.1 與xOy平面平行的平面內的電場分布

在圓環平面(即xOy平面)，有z=0，坐標選擇的范圍為-3a≤x≤3a，-3a≤y≤3a．使用Mathematica的ContourPlot 命令繪制等勢線圖，如圖(2a)所示．其中，等勢線數值參數Contours取30，顏色參數ColorFunction取Hue[#]&，顯示等勢線數值即ContourLabels -> All．從圖中可以看出電勢的分布是內密外疏的軸對稱分布，范圍是1.85 V≤U≤9.62 V．在帶電細圓環的外部區域和內部區域，越靠近圓環電勢越大．值得注意的是，圖中數據表明當電勢較高時(6.29 V≤U≤9.62 V)，等勢線在帶電圓環內外兩側各有一條，而電勢較小時(U≤6.29 V)，等勢線只有一條，分布在圓環外側．使用Plot3D和StreamPlot的命令，分別作出電場強度大小和電場線分布圖，圖2(b)畫出了E≤100 V/m的電場強度，顯然，在圓環周圍區域，越靠近帶電細圓環，電場強度越大．為了更好地顯示電場線與帶電細圓環的對應關系，圖2(c)中使用ParametricPlot命令在電場線圖中加入了帶電細圓環．設圓環帶正電，則電場線的方向在帶電細圓環內外是反向的．圖2(d)將電勢分布和電場線分布組合在一起，形成常見的電場分布圖．

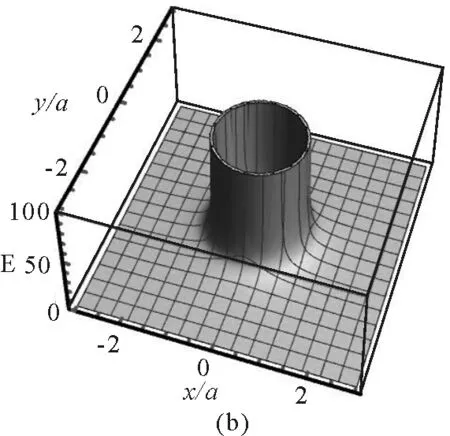
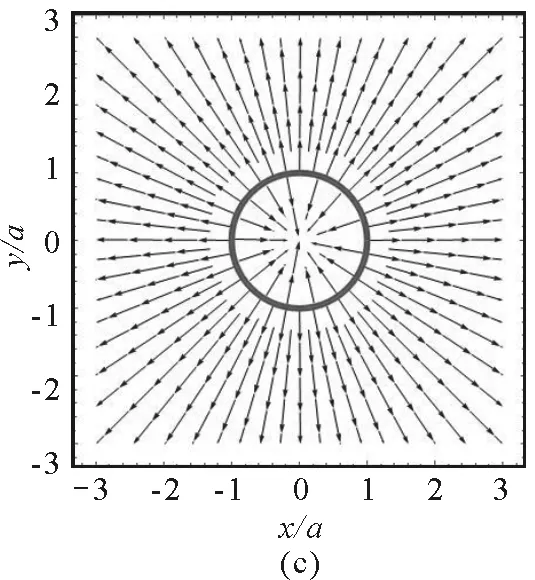
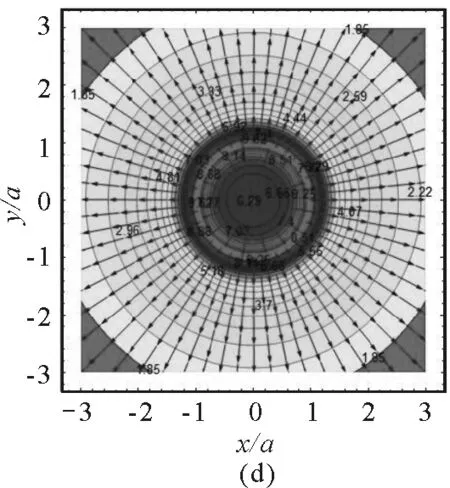
圖2 xOy平面內的電場分布

以上的討論是圓環平面內的電場和電勢分布，那么在與圓環平面平行且z≠0的平面內的電場分布情況如何？對以上程序略做修改即可看到結果.圖3是與xOy平面平行且z=2a平面內的電場強度和電勢與電場線的分布．從圖3(a)可以看出，在該平面內x=0,y=0處的電場強度接近于零，隨著與中心對稱軸線距離的增加，電場先增加后減小，到中軸線的距離接近于a時達到最大值，電場強度E≤0.6 V/m．圖3(b)中電勢的取值范圍為1.41 V≤U≤2.773 V，相對于xOy平面電勢的外疏內密分布，該平面內的電勢分布較為均勻．

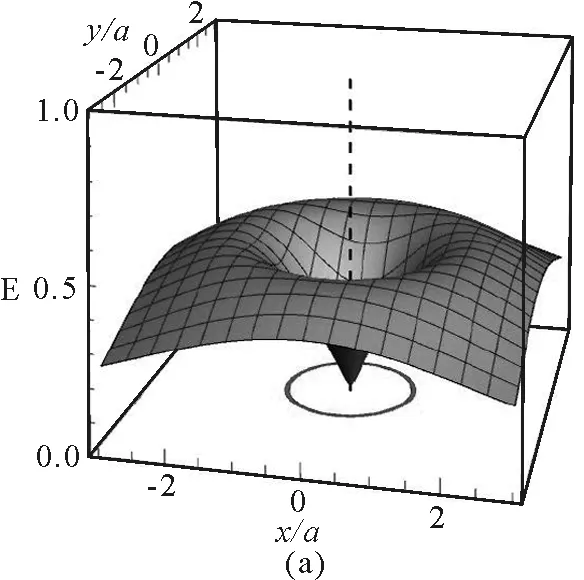
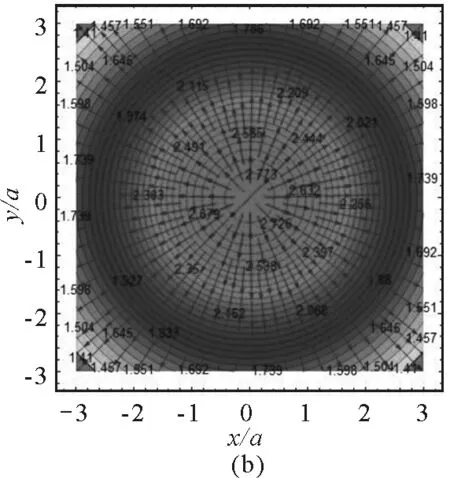
圖3 與xOy平面平行z=2a平面內的電場分布

3.2 與xOy平面垂直的平面內的電場分布

上面討論的是與圓環面平行的平面內的電場分布．那么與圓環面垂直的不同平面內的電場分布呢？我們以xOz平面和與該平面平行的y=a的平面為例進行討論．在xOz平面內的電勢電場分布如圖4所示．

圖4(a)給出的是電勢的分布，從圖中可以看出，等勢線具有明顯的軸對稱性，并且越向外越接近于圓，也就是說，在遠離帶電圓環的區域，電勢的分布類似于將電荷量集中于圓心的點電荷的電勢分布．越靠近帶電細圓環，等勢線變密，為類橢圓．在細圓環內部區域，等勢線又從類橢圓分裂成兩個凸輪的形狀．電勢的范圍為1.7 V≤U≤7.2 V．圖4(b)和圖4(c)分別為電場強度大小和電場線分布．從圖4(b)可以看出，越靠近帶電細圓環，電場強度越大，并且有對稱分布，圖中畫出了E≤30 V/m的電場強度．從圖4(c)可以看出，電場線的分布明顯具有左右對稱性．圖4(d)將電勢分布和電場線分布組合在一起，形成常見的電場分布圖．

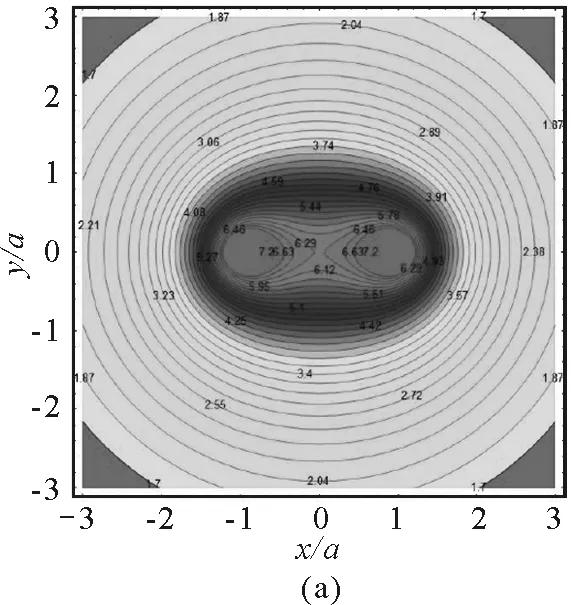
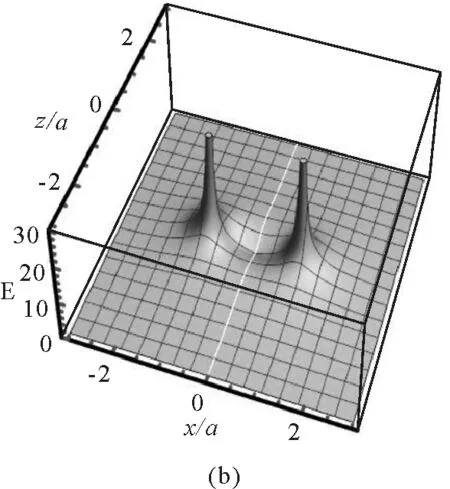
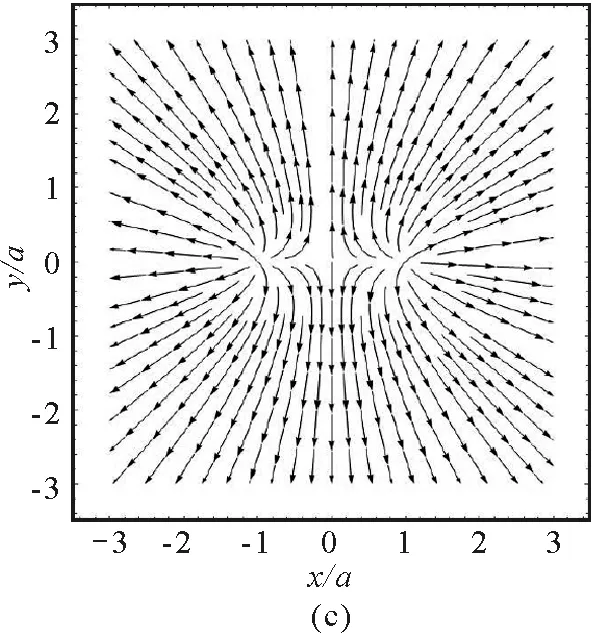
圖4 xOz平面內的電場分布

在與xOz平面平行且y=a的平面，該平面與帶電細圓環相切，位置比較特殊．其電場電勢分布如圖5所示．從圖5(a)可以看出，電場強度已經從左右兩個極值轉換為單極值．從圖5(b)的電勢和電場線分布可以看出，電勢的分布仍然滿足外圓內類橢圓的情況，不同的是，在進入帶電圓環的內部區域后，類橢圓不再分離為凸輪形狀，仍然是一個整體，電勢的范圍為1.54 V≤U≤5.6 V．

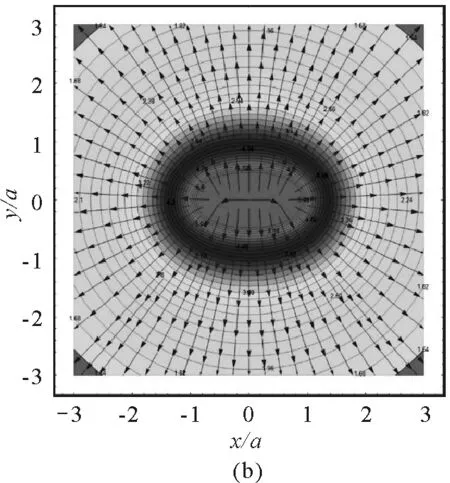
圖5 與xOz平面平行y=a平面內的電場分布

3.3 三維空間的電場分布

需要說明的是，在圖中中心畫出的帶電圓環并不是計算結果，而是為了清晰地顯示帶電圓環的電場分布，使用ParametricPlot3D命令加在電場線中額外附加的．

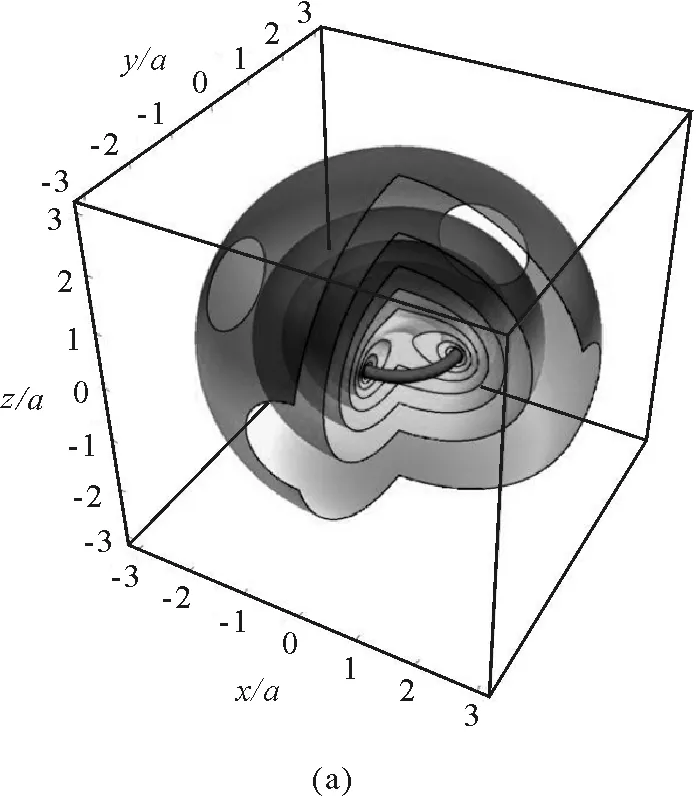
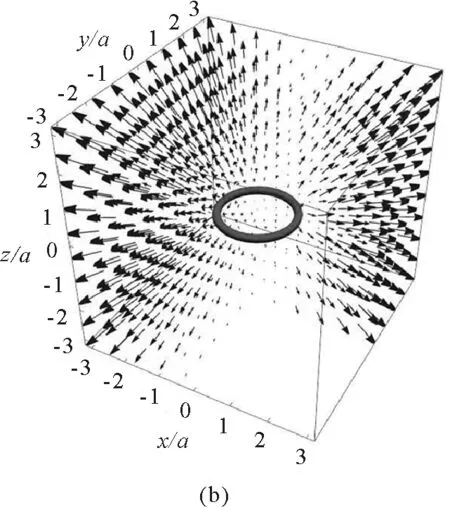
圖6 三維空間的電場分布

4 結論

本文應用Mathematica軟件對均勻帶電細圓環全空間的電場和電勢分布進行了討論，繪制了不同觀察角度下的電場和電勢圖，深入分析了圓環周圍不同位置電場的特點，最后還畫出了三維空間的電場和電勢分布．通過電場可視化，使得抽象的問題變得形象，枯燥的電場變得生動起來，非常有助于提高教學效果．