基于啟發式強化學習的動態CRE偏置選擇算法

谷 靜,鄧逸飛,張 新

(西安郵電大學 電子工程學院,西安 710121)

0 概述

第五代移動通信技術(5G)具有超高的頻譜利用率和能效,和第四代移動通信技術(4G)相比,其傳輸速率和資源利用率提高了至少一個數量級,并且在無線覆蓋、傳輸時延、系統安全和用戶體驗等方面也有顯著提高[1]。異構網絡作為第三代合作伙伴計劃(3GPP)組織在長期演進(Long Term Evolution,LTE)系統中所提出的網絡種類,在4G網絡中解決了業務多樣性的問題。但是,在異構網絡中位于低功率基站附近和宏小區邊緣的宏用戶設備(Macro User Equipment,MUE)會受到低功率基站較強的信號干擾,因此,3GPP組織在長期演進擴展(Long Term Evolution-Advanced,LTE-A)通信系統中引用了小區范圍擴展(Cell Rang Expansion,CRE)技術[2],以均衡宏基站與微基站之間的負載。由于引入CRE后宏小區邊緣的用戶設備依然受到較強的信號干擾,因此擴展區域中的小區間干擾協調(Inter Cell Interference Coordination,ICIC)成為研究人員關注的熱點。

文獻[3]提出家庭基站(Femtocell)合作模型CRE框架,提高了家庭基站接入點范圍擴展系統的靈活性,但未提高宏小區邊緣用戶的通信質量。文獻[4]提出一種分布式自適應CRE偏置方法,其基站間信息交互不足,CRE偏置不能達到全局最優。文獻[5-7]有效提高了宏小區用戶的整體吞吐量并實現了基站負載均衡,但所用算法過程過于復雜。文獻[8]針對上行鏈路干擾提出一種虛擬軟切換方法,該方法對邊緣用戶信干噪比的提升效果較差。文獻[9]提出一種基于大數據驅動框架和多臂Bandit算法的在線學習機制,但其樣本數量過少,不符合實際要求。

本文提出一種基于啟發函數的HSARSA(λ)算法,以動態設置Femto基站(Femto-Base Station,FBS)的CRE偏置值。每個FBS獨立地從經驗中學習CRE偏置值,從而最大限度地提高宏小區邊緣用戶的整體通信速率,實現較好的負載均衡效果。

1 系統模型與偏置方法

1.1 系統模型

本文系統由雙層異構網絡構成,可供選擇的低功率基站有微基站(Pico-Base Station,PBS)、FBS以及中繼基站(Relay-BS,RBS),如圖1所示。該系統選擇FBS作為低功耗基站,這是因為近年來超過80%的無線數據吞吐量發生在室內,在上述低功率基站中,FBS體積最小,部署最靈活且成本最低,網絡安全性能較高,研究FBS的性能可以更好地解決室內通信問題[10]。在系統中隨機分布n個用戶設備,其中包括m個MUE以及k個微用戶設備(Femto User Equipment,FUE)。所有用戶設備采用開放式接入(Open Access,OA)方式,和封閉式接入(Closed Access,CA)相比,OA在用戶設備密度較大時優勢更加明顯[11]。

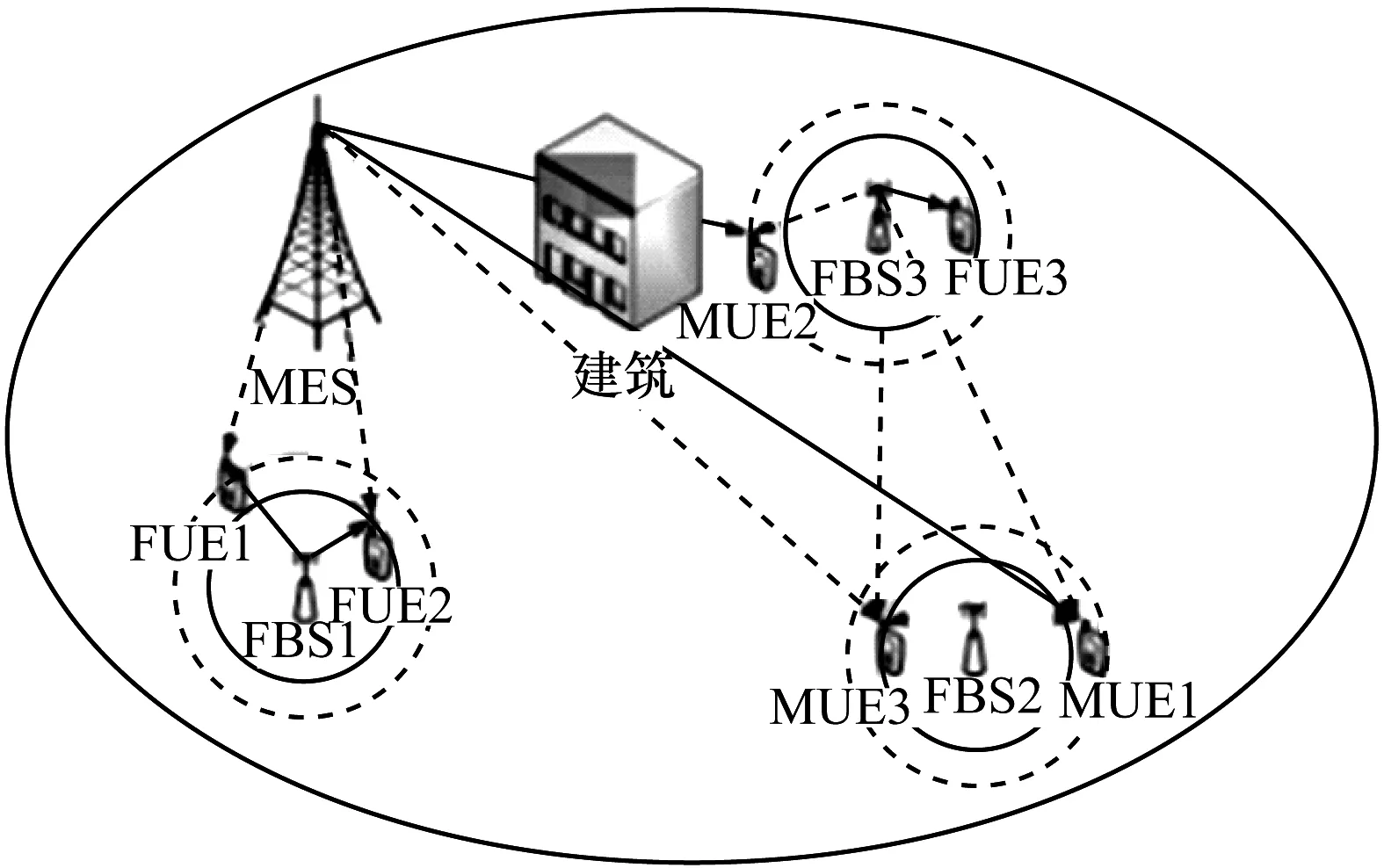
圖1 雙層異構網絡示意圖

FBS的傳輸功率一般為23 dB～30 dB,在存在宏基站(Macro Base Station,MBS)的情況下,FBS的傳輸速率范圍將變小。MBS的發射功率約為45 dB,與FBS的傳輸功率最少相差16 dB,這使得有過多用戶接入MBS,從而造成MBS過載和能效降低的現象,進而導致FBS功率資源浪費。系統中的上行鏈路并非如此,上行鏈路中不同基站(Base Station,BS)的信號強度主要取決于其在上行鏈路的傳輸功率[12],因此,本文系統只考慮下行鏈路的傳輸功率。

圖1中的實線為小區當前的范圍,虛線為小區應調整的范圍。將分布在不同小區的FBS、MUE、FUE分別編號為FBS1、FBS2、FBS3、MUE1、MUE2、MUE3、FUE1、FUE2、FUE3等。系統主要存在以下3種干擾情況:

1)FBS1距MBS較近,FUE1位于FBS1小區邊緣且距MBS也較近,這時FUE1將受到MBS較強的信號干擾,應降低FBS1的CRE偏置值使FUE1接入MBS。

2)MUE1位于MBS小區邊緣處且距MBS較遠,MUE1距FBS2很近但位于FBS2小區邊緣外。MUE1經過長距離路徑損耗與陰影衰落后接收到的MBS信號質量大幅降低,同時還會受到來自FBS2與FBS3下行鏈路的信號干擾,應增大FBS2的CRE值使MUE1接入FBS2。

3)MUE2到FBS3的距離與MUE2到MBS的距離相差不大,但MUE2位于建筑物后,導致其接收MBS信號受阻。因此,在MBS信號覆蓋較弱的建筑密集區,應增大FBS3的CRE偏置值使MUE2接入FBS3。

總結以上3種情況,本文將針對同層與跨層干擾使各種類型基站邊緣用戶的通信質量與通信速率下降等問題進行分析。在下行鏈路中,根據系統模型,第i個MUE的信干噪比為:

(1)

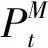
由文獻[3]得到路徑損耗公式為:

PLm=c(dM)n

(2)

其中,c為常數,dM為用戶到基站的距離,n為介質指數。

將式(2)代入式(1)中得到式(3):

(3)

同理可得到第i個FUE的信干噪比為:

(4)

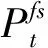
由香農公式可得第i個MUE到MBS的通信速率為:

(5)

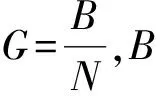
同理可得第i個FUE到第k個PBS的通信速率為:

(6)

所有用戶的總通信速率為:

(7)

總用戶功耗[13]為:

PMD=N[PW·Rt+Ps(1-Rt)]

(8)

其中,PW為用戶活躍時的總功耗,PS為用戶非活躍時的總功耗。系統最終能效為:

(9)

其中,PMA為系統總功耗,PBS為MBS的發射功率,S為宏小區的面積。

1.2 CRE偏置方法

本文在考慮參考信號接收功率(Reference Signal Received Power,RSRP)大小的基礎上,通過評估導頻信號(參考信號)的強度來觸發移交程序。用戶在比較來自各基站參考信號的功率大小后,會連接到信干噪比相對較高的基站。此外,使用CRE將偏壓值加到FBS發射信號上可使更多的用戶連接到FBS,相當于將FBS小區范圍人為擴大。若MBS和PBS的發射功率滿足以下關系:

此時,用戶會連接到MBS。若MBS和PBS的發射功率滿足以下關系:

此時,用戶會連接到FBS。MBS和PBS的發射功率差會使得邊緣用戶受到相鄰小區基站信號的干擾[12],因此,需要通過調整CRE偏置值(Δbias)來降低邊緣用戶受到的干擾。

傳統經驗將CRE偏置值設定為6 dB,華為公司提供的GRE偏置值為9 dB。下文以邊緣用戶的平均吞吐量為參考來尋求合理的GRE偏置值。

2 基于HSARSA(λ)算法的CRE偏置選擇

通過調整GRE偏置值來降低邊緣用戶受到的干擾,既要考慮各基站間的信息交互,又要根據時延與用戶分布的變化來動態調整偏置值。經驗偏置值與其他算法基本無法簡單有效地解決最佳偏置值的選擇問題。為此,本文在強化學習(Reinforcement Learning,RL)的基礎上提出一種基于啟發函數的改進SARSA(λ)算法,即HSARSA(λ)算法。和SARSA(λ)算法相比,HSARSA(λ)算法的獎賞反饋更快,其學習性能顯著提高。

2.1 強化學習與SARSA(λ)算法

RL是人工智能體實現自主行為的理論基礎,其對策略和狀態具有強大的表征能力,能夠模擬復雜的決策過程。RL還賦予人工智能體自監督學習能力,使其能夠自主與環境交互,在試錯(Trial and Error)中不斷進步[14]。RL作為人工智能領域的一個重要分支,被認為是實現類人工智能的關鍵,受到學術界和工業界的廣泛關注。RL主要以馬爾科夫決策過程為基礎,該過程用狀態(State)、動作(Action)、狀態轉移率(Possibility)和獎賞(Reward)構成的四元組{s,a,p,r}表示[15]。其中,動作與狀態構成動作狀態表,用以表示在某種狀態下對根據策略π執行的動作進行的價值評估,也稱為狀態-動作對值函數,具體如下:

Qπ(s,a)=E(R|st=s,at=a)

(10)

式(10)表示狀態-動作對值函數是在反饋獎賞R下狀態值St等于某一狀態S、動作值at取某一動作a時的數學期望。

最佳Q表值為:

(11)

人工智能體在每種狀態下能獲得最佳動作的策略為:

(12)

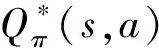
目前,諸如Q-Learning、TD(λ)、SARSA等強化學習算法已經在理論和應用方面取得較多成果[16]。SARSA算法借鑒Q-Learning算法的思想并利用TD算法的核心理論,使得行為決策與值函數迭代的一致性得到保障[17],這表明在學習控制方面SARSA算法優于Q-Learning算法。SARSA(λ)算法在SARSA算法的動作-狀態對值函數更新過程中加入了資格跡,如下:

(13)

其中,γ與λ均為折扣因子。

資格跡是基于有效跟蹤原理形成的多步在線學習理論,其能有效地使原算法在獲得獎賞時更貼近目標值。但是,SARSA(λ)算法在新環境中學習速率較慢,忽略了很多有價值的信息。由于缺乏有效的策略選擇機制,SARSA(λ)算法在狀態空間需要多次遍歷才能收斂。引入啟發函數對SARSA(λ)算法在貪婪選擇與狀態動作對更新時進行改進,可使其在策略選擇與匯報獎賞中取得更快的學習速率和更多的有效信息。

2.2 HSARSA(λ)算法

2.2.1 啟發函數

啟發式強化學習(HARL)采用啟發函數來影響人工智能體在學習中的動作選擇。文獻[18]較早提出啟發加速的Q-Learning算法,啟發函數Ht(st,at)表示在當前狀態下執行此動作的重要性。該方法將經驗值作為啟發信息,給特定行動加以獎賞,并可作為約束條件來縮小搜索范圍使算法更快達到收斂效果。

對于某一狀態st,啟發值Ht(st,at)只有普遍高于值函數Qt(st,at)的變化值時才能影響動作選擇,且要盡量減小誤差。啟發函數與策略緊密相關,選擇動作的策略是決定整個過程是否更接近最優狀態的重要因素。策略從形式上可定義為:

π(s)=argmax[Qt(st,at)+μHt(st,at)β]

(14)

其中,μ∈R,β∈R均為評定啟發函數重要性的參數,數值越大其影響越大。在式(14)的基礎定義下,啟發函數可定義為:

(15)

2.2.2 更新公式

SARSA(λ)算法在選擇動作時使用ε-貪婪策略,HSARSA(λ)算法將ε-貪婪策略改進為:

(16)

上述改進可以使人工智能體在根據策略選擇動作時通過Ht(st,at)來分析動作的優劣,不斷保留優勢摒棄劣勢,有效減少了無用搜索,最終使算法加速收斂。

2.2.3 算法流程

HSARSA(λ)算法將系統模型中的偏置值bi={CRE1,CRE2,…,CREi,…,CREn}和用戶的SINR分布值與HSARSA(λ)算法中的狀態表和動作表相結合。動作是決定最終結果的因素,因此將偏置值CREi的分布設定為動作分布表。狀態是在執行動作后所造成的影響效果。將CRE偏置值代入路徑損耗公式可求出偏置范圍ΔL,根據ΔL可求出邊緣用戶的信干噪比。將調整CRE偏置值后會受影響的用戶信干噪比分布列為狀態表,再根據動作和狀態建立值函數表Qπ(SINRi,bi),HSARSA(λ)算法流程如圖2所示。

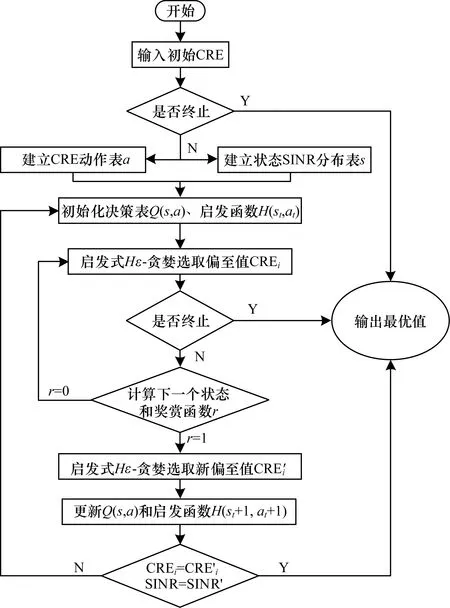
圖2 HSARSA(λ)算法流程

HSARSA(λ)算法的偽代碼為:

Begin:

建立動作表bi

建立狀態表SINRi

初始化Qπ(SINRi,bi),et(SINRi,bi)

For each episode:

Ⅰ.在當前狀態下,用Hε-貪婪策略選取Ht(SINRi,bi)動作bi

Ⅱ.若當前動作不為最優,則重復以下步驟:

B.在當前新狀態SINR′i下,利用Hε-貪婪策略在SINR′i中選擇新的偏置值b′i

Ⅲ.更新Ht(SINR′i,b′i)與Qπ(SINR′i,b′i)

δ=R+γQπ(SINR′i,b′i)-Qπ(SINRi,bi)

et(SINR′i,b′i)=et(SINRi,bi)+1

Ⅳ.更新狀態動作對表

Q′π(SINRi,bi)=Qπ(SINRi,bi)+αδet(SINR′i,b′i)

et(SINR′i,b′i)=γλet(SINR′i,b′i)

直到SINRi=SINR′i,bi=b′i,算法終止

其中,α為學習率

在本文系統中,當人工智能體發現新的狀態時,如果一直將狀態添加到Q表中,Q表值就會增加,這違背了內存約束條件,且會延長學習時間。為解決該問題,使用經驗偏置值以實現更快的收斂。由于經驗偏置值較易得知,在開始學習和發送數據前,可用試錯法檢查所有的經驗偏置值以縮短學習時間。

所有用戶的共同偏置值雖然不是每個用戶的最優偏置值[19],但其通常較接近最優偏置值。引入共同偏置值可減小內存并加快收斂速度。當用戶移動到另一個FBS信號覆蓋區域時,Q表數據即使發生變化也仍具有相似性,在一種情況下獲得的數據也有助于在另一種情況下的學習[20]。使用這些數據作為下一次學習的初始值,即使情況不同,用戶也會學習環境以進行Q表的更新。

3 實驗結果與分析

本文采用蒙特卡羅仿真方法,在Matlab2014R環境下進行實驗。實驗參數如表1所示[10,18],設置1個MBS和6個FBS,結果取20次實驗的平均值。

表1 實驗參數設置

根據服務質量(Quality of Service,QoS)評判標準,本文對系統邊緣用戶的通信速率、能效以及吞吐量進行分析。

從圖3可以看出,通信較差與通信較好的用戶已進行均衡化處理,兩類用戶的通信質量趨于一致,即采用HSARSA(λ)算法得到的CRE偏置值能有效均衡邊緣負載,使整個系統的通信質量得到提高。

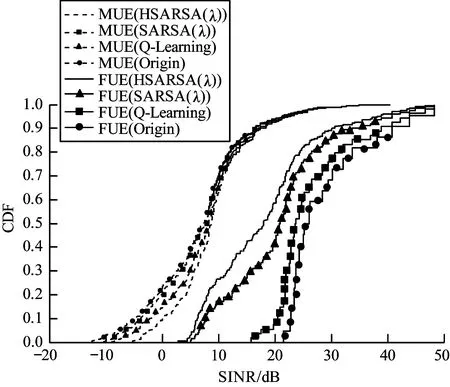
圖3 MUE與FUE的SINR累積分布

從圖4可以看出,隨著用戶分布量的增加,應用Origin、Q-Learning、SARSA(λ)和HSARSA(λ) 4種算法得到的系統用戶平均吞吐量逐漸上升。當用戶分布量超過0.3時,系統用戶的平均吞吐量均顯著上升,當用戶分布量為0.5～0.7時,應用HSARSA(λ)算法得到的系統用戶平均吞吐量比SARSA(λ)算法高約7%,比Q-Learning算法高約15%。

圖4 不同算法的系統用戶平均吞吐量分布

Fig.4 Average throughput distribution of system users of different algorithms

從圖5可以看出,隨著邊緣用戶分布量的增加,應用Origin、Q-Learning、SARSA(λ)和HSARSA(λ) 4種算法得到的系統邊緣用戶的平均吞吐量逐漸提升。當邊緣用戶分布量為0.6～0.8時,應用HSARSA(λ)算法得到的系統邊緣用戶平均吞吐量比SARSA(λ)算法高約6%,比Q-Learning算法高約12%。由此可知,HSARSA(λ)算法可使系統邊緣用戶的吞吐量得到較大提升。

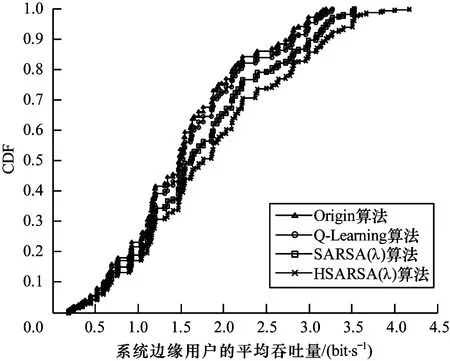
圖5 不同算法的系統邊緣用戶平均吞吐量分布

Fig.5 Average throughput distribution of system edge users of different algorithms

從圖6可以看出,HSARSA(λ)算法的平均能效最高,該算法在保證宏小區基本通信質量的前提下可大幅提高小區邊緣用戶的通信速率。HSARSA(λ)算法的平均能效比SARSA(λ)算法高11%,比Q-Learning算法高13%。

圖6 不同算法的平均能效對比

Fig.6 Comparison of average energy efficiency of different algorithms

從圖7可以看出,隨著學習幕數的增加,Q-Learning、SARSA(λ)和HSARSA(λ)算法尋找最優CRE偏置值的步數逐漸減少。當學習幕數為15節時,HSARSA(λ)算法已收斂,SARSA(λ)、Q-Learning算法的收斂速率分別為40和60。HSARSA(λ)算法收斂時步數小于Q-Learning、SARSA(λ)算法,這表明HSARSA(λ)算法的收斂速率和搜索效率比其他2種算法更優。從圖8可以看出,隨著學習幕數的增加,Q-Learning、SARSA(λ)和HSARSA(λ)算法獲得獎賞的數量均呈現出先降后增的趨勢。當學習幕數為0～15節時,3種算法獲得獎賞的數量均逐漸降低,其中,HSARSA(λ)算法的降幅最小。當學習幕數超過15節時,HSARSA(λ)算法獲得的獎賞數量逐步上升。在學習幕數增加的過程中,當學習幕數相同時,HSARSA(λ)算法得到的獎賞更多,這表明HSARSA(λ)算法每步搜索的結果均比其他2種算法更接近最佳值。

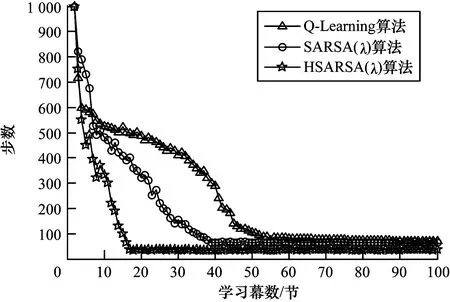
圖7 不同算法的收斂性能對比

Fig.7 Comparison of convergence performance of different algorithms

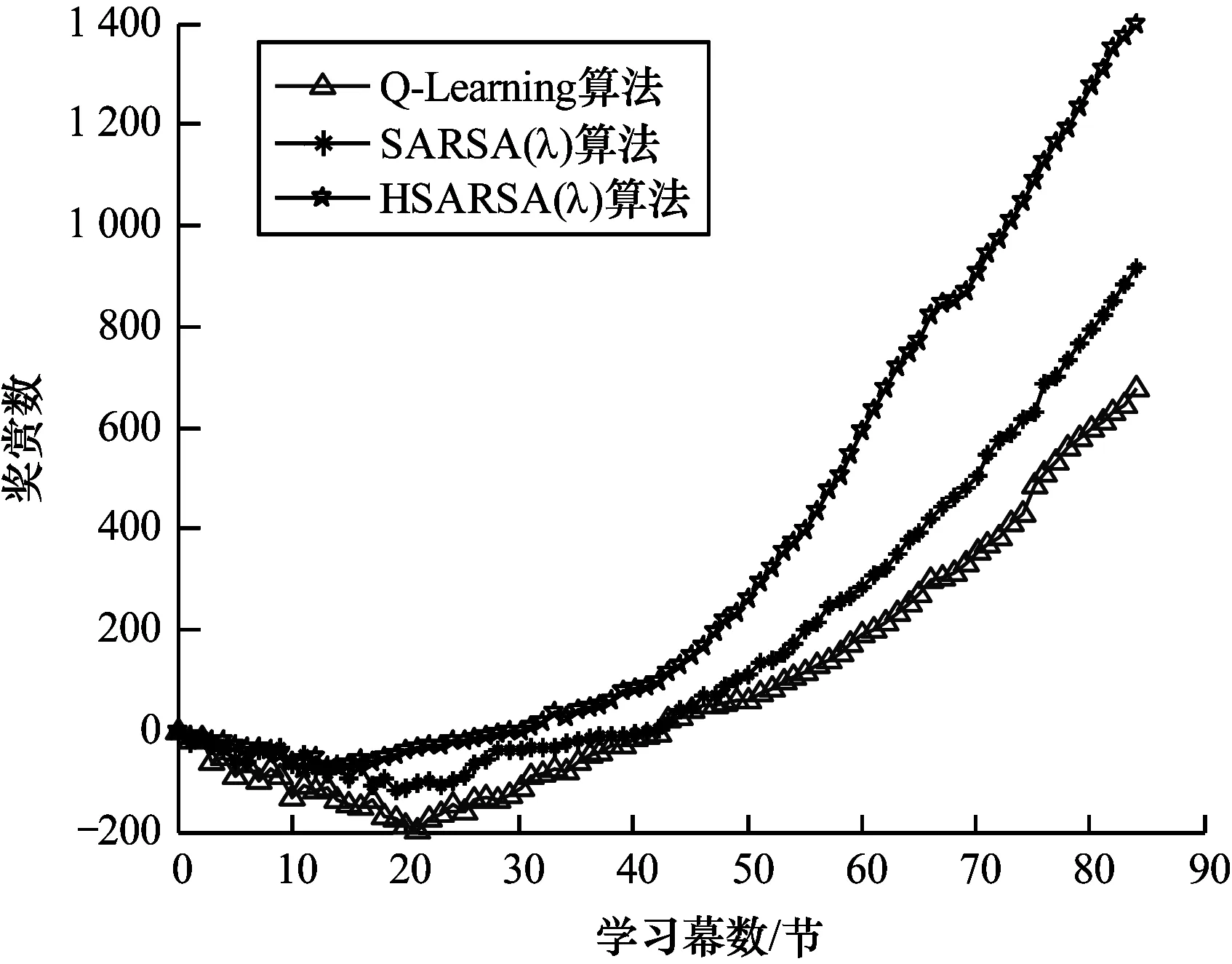
圖8 不同算法獲得獎賞的能力對比

Fig.8 Comparison of ability of different algorithms to obtain rewards

4 結束語

本文采用啟發函數對強化學習中的SARSA(λ)算法進行改進,提出一種HSARSA(λ)算法,以動態設置FBS的小區范圍擴展偏置值。該算法使宏基站功率資源卸載分流的同時使得微基站功率資源得到充分利用,從而實現系統的負載均衡。仿真結果表明,相比Q-Learning、SARSA(λ)算法,HSARSA(λ)算法的收斂速率和用戶通信速率較高,其能同時保證宏用戶與邊緣用戶的通信質量。下一步將在本文算法的基礎上研究頻譜資源的有效利用問題,以提升系統的通信質量。