直角坐標平面內兩點在該平面折疊后的距離

張光俊

（金陽縣初級中學，四川 金陽 616250）

在直角坐標平面xoy 內，對于兩定點P1(x1,y1)，P2(x2,y2)，定直線l:Ax+By+C=0，若將平面xoy 沿直線l 折成大小為θ 的二面角，則折疊后P1，P2的距離應該是確定的，即應該可以用P1，P2的的坐標、l 的方程的系數以及θ 來表示，本文的研究目的就是尋求這樣的表達.為此我們需要如下幾個引理.

1 預備知識

引理1在直角坐標平面xoy 內，設點P1(x1,y1)，P2(x2,y2)，直線l:f(x,y)=Ax+By+C=0，

（i）若f(x1,y1)f(x2,y2)＞0，則P1、P2在l 的同側；

（ii）若f(x1,y1)f(x2,y2)=0，則P1或P2在l 上；

（iii）若f(x1,y1)f(x2,y2)＜0，則P1、P2在l 的異側.

證明：（ii）顯然，（i）、（iii）證明類似，這里只證（iii）.

（iii）由f(x1,y1)f(x2,y2)＜0，則Ax1+By1+C 與Ax2+By2+C 異 號，不 妨 設Ax1+By1+C ＞0，Ax2+By2+C ＜0.

引理2設直角坐標平面xoy 內，直線l:Ax+By+C=0，直線l′⊥l，且l′過點P0(x0,y0)，則l′的方程是Bx-Ay-(Bx0-Ay0)=0.

證明：若l⊥x 軸，則B=0，A ≠0，由l′⊥l，故l′⊥y 軸，又l′過點P0(x0,y0)，故l′的方程是y=y0，即Bx-Ay-(Bx0-Ay0)=0.

若l⊥y 軸，則A=0，B≠0，由l′⊥l，故l′⊥x 軸，又l′過點P0(x0,y0)，故l′的方程是x=x0，即Bx-Ay-(Bx0-Ay0)=0.

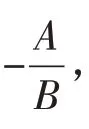
引理3設直角坐標平面xoy 內兩平行直線l1:Ax+By+C1=0，l2:Ax+By+C2=0，則l1,l2間的距離為

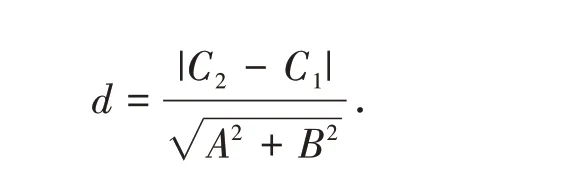
證明：在l1上任取一點P0(x0,y0)，則Ax0+By0+C1=0，故Ax0+By0=-C1.又l1//l2，故l1,l2間的距離d 即點P0到l2的距離，所以

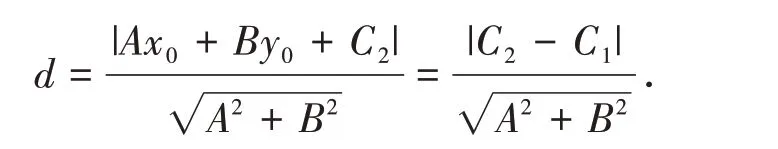
引理4[1]設二面角α-l-β 的大小為θ，點A ∈α，點B ∈β，AC⊥l 于C，BD⊥l 于D，如圖1 所示，記AC=m，BD=n，CD=d，則

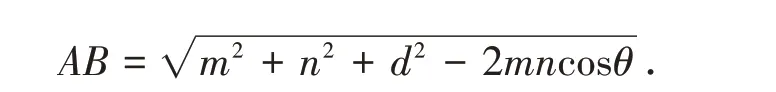
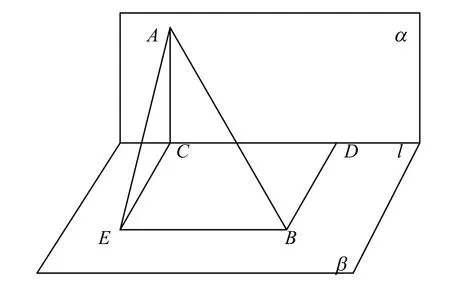
圖1

證明：在β 內作BE//l，CE//DB，BE 與CE 交于E，則BDCE 為矩形，CE=DB=n，CE⊥l 于C，EB=CD=d，∠ACE 即為二面角α-l-β 的平面角，即∠ACE=θ，連接AE，故由余弦定理

AE2=AC2+CE2-2AC ?CEcosθ=m2+n2-2mncosθ，

又顯然l⊥平面ACE，故EB⊥平面ACE，從而EB⊥AE，所以

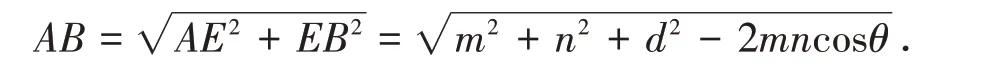
注：引理4 的結論來源于文[1]，但這里的證明方法并不同于文[1].

2 主要結論

定理在直角坐標平面xoy 內，設點P1(x1,y1)，P2(x2,y2)，直線l:f(x,y)=Ax+By+C=0，將平面xoy沿直線l 折成大小為θ 的二面角，折疊前后P1，P2的距離分別記為|P1P2|和P1P2，則

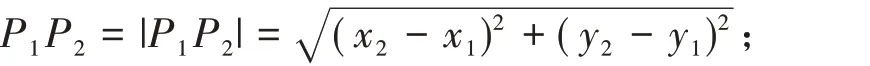
（ii）當f(x1,y1)f(x2,y2)＜0 時，

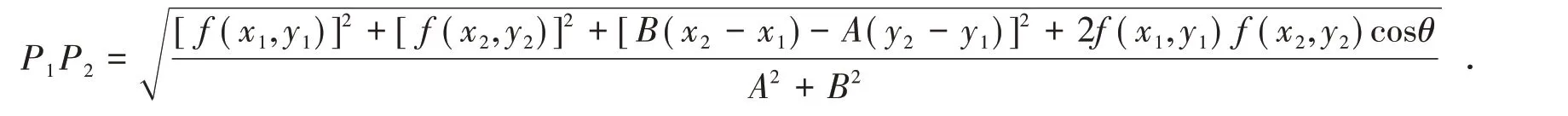
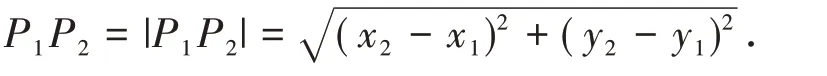
（ii）當f(x1,y1)f(x2,y2)＜0 時，則由引理1，P1、P2在l 的異側.為方便，以下所作圖形都省掉坐標軸，圖2 是折疊前，圖3 是折疊后（用了兩個半平面襯托），作P1M⊥l 于M，P2N⊥l 于N.

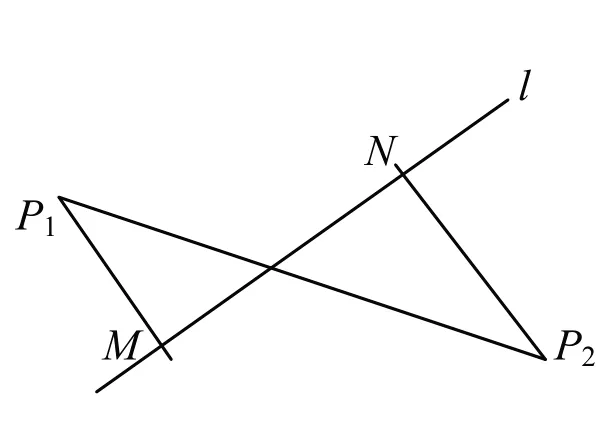
圖2

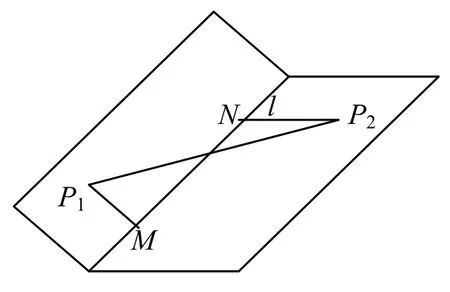
圖3

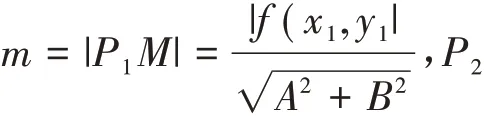
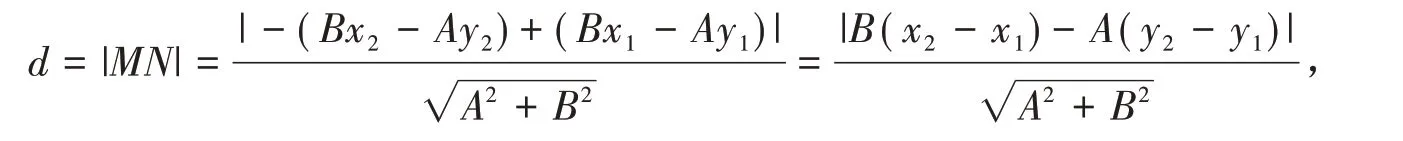
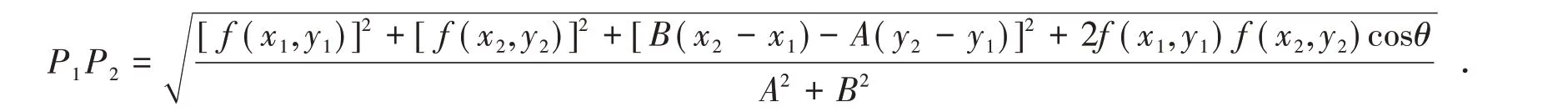
3 應用舉例

例 在直角坐標平面xoy 內，已知點P(-1,3)，Q(2,1)，直線l:2x-y+2=0，PQ 交l 于R，將平面xoy 沿l 折成大小為θ 的二面角，使∠PRQ=1200，求θ.

解 記l:f(x,y)=2x-y+2=0，則f(-1,3)=-3 ＜0，f(2,1)=5 ＞0，由引理1 知P,Q 在l 的異測，則由定理可得折后

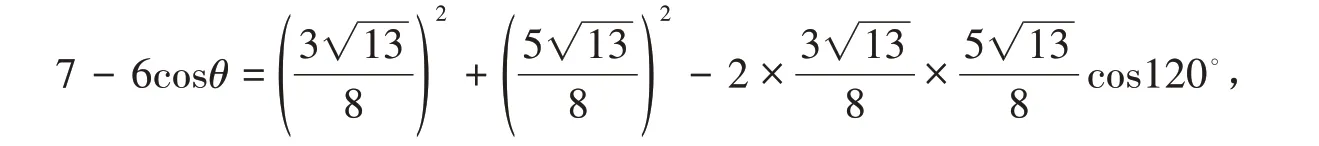
由余弦定理得而折后∠PRQ=120°，