基于二階時序差分誤差的雙網絡DQN算法

陳建平,周 鑫,傅啟明,高 振,付保川,吳宏杰

(蘇州科技大學 a.電子與信息工程學院; b.江蘇省建筑智慧節能重點實驗室,江蘇 蘇州 215009)

0 概述

強化學習(Reinforcement Learning,RL)是一種通過與環境交互將狀態映射到動作以獲取最大累積獎賞值的方法[1]。該方法設計思想來源于條件反射理論和動物學習理論,是一類重要的機器學習算法。自20世紀80年代被提出以來,經過不斷發展,強化學習已經在工程設計、模式識別、圖像處理、網絡優化等方面得到了廣泛應用[2]。由于強化學習方法特有的學習和計算方式,其在解決一些大規模或連續的狀態空間任務時,狀態空間的大小隨著特征數量的增加而呈指數級增長趨勢,所需計算量和存儲空間也指數級增長,導致“維數災難”[3]問題,因此,傳統的強化學習方法無法滿足大狀態空間或者連續狀態空間的任務需求。目前,解決“維數災難”問題的主要方法是狀態抽象和函數逼近。其中,函數逼近可以有效減少狀態的存儲空間,并且在大規模數據的訓練中具備一定的泛化特性。

在解決大規模狀態空間的強化學習問題時引入深度學習(Deep Learning,DL)[4-5]可實現復雜函數的逼近。深度學習的概念源于對人工神經網絡的研究,其通過學習一種深層的非線性網絡結構,擬合數據與標簽之間的非線性關系,從而學習數據的本質特征[6],實現復雜函數的逼近。谷歌的DeepMind團隊在此基礎上創新性地將具有決策能力的強化學習與具有感知能力的深度學習相結合,提出了深度強化學習(Deep Reinforcement Learning,DRL)[7]的概念。此后,DeepMind構造了人類專家級別的Agent,其對自身知識的構建與學習都來源于原始輸入信號,無需任何人工編碼和領域知識,充分體現了DRL是一種端到端的感知與控制系統,具有很強的通用性[8]。此后,深度強化學習被廣泛應用于各種問題,如AlphaGo[9]、對抗網絡架構[10]、機器人控制[11-12]等。

在深度強化學習概念出現之前,研究者主要將神經網絡用于復雜高維數據的降維,以便于處理強化學習問題。文獻[13]結合淺層神經網絡與強化學習解決視覺信號輸入問題,控制機器人完成推箱子等任務。文獻[14]提出視覺動作學習的概念,將高效的深度自動編碼器應用于視覺學習控制中,使智能體具有與人相似的感知和決策能力。文獻[15]通過結合神經演化方法與強化學習,在賽車游戲TORCS中實現了賽車的自動駕駛。文獻[16]將深度置信網絡引入到強化學習中,用深度置信網絡替代傳統的值函數逼近器,成功應用于車牌圖像的字符分割任務。文獻[17]采用Q學習構建誤差函數,利用深度神經網絡優化蜂窩系統的傳輸速率。文獻[18]將卷積神經網絡與傳統RL中的Q學習[19]算法相結合,構建深度Q網絡(Deep Q-Network,DQN)模型用于處理視覺感知的控制任務。此后,DeepMind團隊結合DQN模型與目標Q網絡模型對原始的DQN模型進行改進,進一步提升其處理視覺感知任務的能力[20]。文獻[21]提出基于時序差分(Temporal Difference,TD)誤差自適應校正的DQN主動采樣方法,估計樣本池中樣本的真實優先級,提高了算法的學習速度。

本文針對原始DQN算法因過估計導致穩定性差的問題,提出一種基于二階TD誤差的雙網絡DQN算法(Second-order TD-based Double Deep Q-learning Network,STDE-DDQN)。通過構造2個相同的DQN結構協同更新網絡參數,并且基于二階TD誤差重構損失函數,從而增強學習過程中值函數估計的穩定性。

1 相關理論

1.1 馬爾科夫決策過程

馬爾科夫決策過程(Markov Decision Process,MDP)可以用來解決序貫決策問題,而強化學習任務是一個典型的貫序決策過程。因此,利用馬爾科夫決策過程對強化學習問題進行建模,可以有效解決強化學習任務。

在強化學習中,通過估計動作值函數可以衡量Agent在某一策略π下動作選擇的優劣程度,其中,優劣程度根據可以利用的未來累積獎賞進行評估。策略π是指在狀態s下采取動作a的概率,可以表示為π(s,a)。動作值函數Qπ的定義如式(1)所示:

Qπ(s,a)=Eπ{Rt|st=s,at=a}=

(1)

其中,γ是折扣率,決定著未來獎賞的當前價值。如果當前策略是最優策略,則所對應的動作值函數即為最優動作值函數Q*,定義如式(2)所示:

(2)

1.2 時序差分學習

時序差分(TD)學習結合了蒙特卡洛和動態規劃思想,能夠從原始的經驗中學習,是一種模型無關的強化學習方法。

TD方法對狀態值函數進行評估,可以利用經驗樣本解決預測問題。通過判斷學習過程中行為策略與目標策略是否一致,可以將TD學習分為兩類:在策略學習與離策略學習。Q學習算法是一種經典的離策略算法,行為策略一般使用ε-greedy策略。此外,基于Q學習對動作值函數進行評估,可以用于解決控制問題。Q學習中的Q值函數更新公式如式(3)所示:

Q(st,at)←Q(st,at)+β[rt+1+

(3)

其中,β是學習率,rt+1是立即獎賞,γ是折扣率。在這種情況下,學到的動作值函數Q直接逼近最優動作值函數Q*,且不依賴于其行為策略。

1.3 DQN算法

DQN算法將深度學習與強化學習相結合,直接從高維的輸入學習控制策略,實現“端到端”的學習。該算法模型利用神經網絡逼近動作值函數,通過經驗回放解決數據相關性及非靜態分布問題,并使用目標網絡解決模型穩定性問題。相較于其他模型,DQN具有較強的通用性,可用于解決不同類型的問題。

在DQN算法中包含兩個相同的網絡:目標網絡和估值網絡。初始化時,兩個網絡的權值相同。在訓練過程中,對估值網絡進行訓練更新,通過直接賦值的方式對目標網絡進行權值更新。

在每一次的迭代更新過程中,從經驗池中隨機抽取小批量樣本(st,at,rt,at+1),將st輸入估值網絡,輸出在狀態st下每一個動作的Q值,即估值網絡的預測值Q(st,at)。在訓練過程中,通過求解標簽值對估值網絡進行權值更新。在計算標簽值時,將st+1輸入目標網絡,輸出在st+1狀態下每個動作對應的最大Q值,即Q*(st+1,at+1),使得累積折扣獎賞最大。同時,每訓練N步,則將估值網絡的權值賦值給目標網絡,進行一次更新。

DQN模型通過Q學習中的TD誤差構造如下損失函數:

(4)

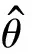
然而,利用式(4)求解損失函數時,目標網絡Q值的迭代過程采用max操作。由式(5)可知,對Q值進行max操作后,其比優先計算目標Q值期望后進行max操作的值大。因此,在原始DQN算法中,利用目標網絡最大Q值替代目標網絡Q值期望值的計算,會導致目標Q值的計算存在過估計,從而造成算法收斂性能的不穩定。

E(max(Q1,Q2))≥max(E(Q1),E(Q2))

(5)

2 基于二階TD誤差的雙網絡DQN算法

在原始DQN模型中,目標Q值的計算存在過估計,會導致損失函數的計算出現偏差,降低算法收斂穩定性。針對該問題,本文提出一種基于二階TD誤差的雙網絡DQN算法。在DQN模型的基礎上增加一個相同的值函數網絡,并提出二階TD誤差的概念,構建二階TD誤差模型與新的損失函數更新公式。通過兩輪值函數的學習,降低目標Q值最大化的影響,克服單一目標Q值計算存在過估計的問題,有效減小模型的計算誤差,提高算法中值函數估計的穩定性。

2.1 雙網絡DQN模型

針對DQN算法由于過估計導致收斂性差的問題,結合TD誤差階的定義,在DQN的基礎上增加一個相同的值函數網絡模型,從而提高算法的收斂性能,改進后的結構模型如圖1所示。

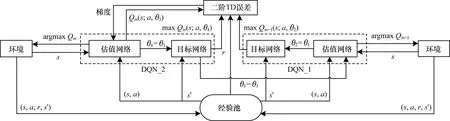
圖1 基于二階TD誤差的雙網絡DQN模型結構

在圖1中,為保證二階TD誤差雙網絡結構的穩定性,設置DQN_1與DQN_2結構中的初始化權重參數θ相同。在二階TD模型中,DQN_2的估值網絡與環境交互,將得到的數據存入經驗池,同時自動更新參數,將估值網絡中的參數傳遞給DQN_1中的估值網絡。在DQN_2與環境第1輪交互后,DQN_1與環境交互,Agent進行第2輪的學習。

在第2輪學習結束后,Agent在前兩輪學習的基礎上,通過DQN_1目標網絡中的動作值函數與DQN_2結構中估值網絡和目標網絡中的動作值函數,構建新的損失函數,利用梯度下降對權重進行求解,以逼近真實目標Q值。之后,在DQN_2上進行第3輪學習,直至所有的情節結束。此外,每間隔N步,DQN_1與DQN_2模型中的估值網絡都會將權重參數復制給各自的目標網絡。

2.2 二階TD誤差

在任意第m次迭代計算中,任意時刻t,當前狀態動作對為(st,at),Q學習以前一輪對(st,at)的估計差值作為TD誤差,如式(6)所示:

TDEm(st,at)=βt[rt+1(st,at)+

γmaxQm-1(st+1,at+1)-Qm-1(st,at)]

(6)

其中,TDEm(st,at)是在第m輪中t時刻狀態動作對的TD誤差,βt是學習率,rt+1(st,at)是該狀態動作對的立即獎賞值,γ是折扣率,Qm-1(st+1,at+1)是m-1輪中t+1時刻的狀態動作對的估值,Qm-1(st,at)是m-1輪中t時刻的狀態動作對的估值。在式(6)中,當前狀態動作值的估值是基于后續狀態動作對估值的最大值,即利用后續狀態動作對的Q值的極值,代替狀態動作對的真實極值,進而計算TD誤差。

定義1(N階TD誤差) 在第m輪,任意時刻t,立即獎賞為rt+1,記Q值為:

Qm(st,at)=rt+1+γmaxQm(st+1,at+1)

(7)

其中,Qm(st+1,at+1)是第m輪對t+1時刻狀態動作對的估值。N階TD誤差的定義如式(8)所示,記為TDE(n),并且n≥1,n為階數。當n為2時,稱為二階TD誤差,記為TDE(2),如式(9)所示:

(1-αm){αm[Qm-n(st,at)-Qm-1(st,at)]+

(8)

(1-αm)[Qm-1(st,at)-Qm-2(st,at)]

(9)

2.3 損失函數構建

算法的實際輸出與期望輸出差值越大,即損失函數的值越大,算法的收斂效果越差。本文針對算法收斂穩定性問題,構造兩個相同的DQN結構,引入二階TD誤差的概念重構新的損失函數,達到提升算法收斂性能的目的。

在DQN模型的學習過程中,從經驗池隨機選擇樣本數據,通過梯度下降的方式進行參數更新。在二階TD誤差雙網絡DQN結構中,利用經驗回放進行隨機采樣,通過二階TD誤差函數進行學習,并更新權重參數θ。二階TD誤差計算公式如式(10)所示:

(α-1)[Qm-1(st,at;θ4)-Qm-2(st,at;θ2)]

(10)

其中,θ2為DQN_1模型目標網絡的參數,θ3與θ4分別為DQN_2模型中估值網絡和目標網絡的參數。在模型訓練的每一步參數更新過程如下:將DQN_2中估值網絡的參數傳遞給DQN_1中的估值網絡,且同時保持自身的更新,即θ3=θ1,θ3=θ3,其中θ3表示DQN_2中估值網絡下一狀態的權重參數,每間隔N步,將DQN_1中的估值網絡參數傳遞給目標網絡,即θ2=θ1,同時將DQN_2中的估值網絡參數傳遞給目標網絡,即θ4=θ3。

由此得到改進后的損失函數如式(11)所示:

L(θ)=Es,a,r,s′{[(1-α)(TQ2-TQ1)-

α(TQ1-BQ2)]2}

(11)

其中,損失函數是兩個網絡參數值的方差,并受參數α的影響,網絡結構的目標值與估計值也取決于網絡權重參數。在訓練時,要保持當前目標網絡權重參數的固定,防止算法收斂不穩定。對損失函數式(11)求解權重導數,得到權重梯度如式(12)所示:

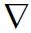
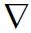
(12)

2.4 STDE-DDQN算法

根據上文介紹,給出基于二階TD誤差雙網絡DQN算法流程,如算法1所示。

算法1基于二階TD誤差的雙網絡DQN算法

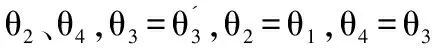
2.For episode=1,M do

3.初始化狀態s1;

4.For t=1,T do

5.采用ε-greedy策略選擇動作;

6.得到執行動作at后的獎勵r,以及下一時刻的狀態st+1;

7.將數據(st,at,rt,st+1)存入到D中;

8.隨機從D中取出樣本(st,at,rt,st+1)進行訓練;

9.判斷狀態是否為中止狀態,若是則目標為rT,否則計算目標值;

10.利用式(11)計算損失函數;

11.利用式(12)更新權重參數θ1與θ3;

12.每N步迭代后,θ2=θ1,θ4=θ3;

13.End for

14.End for

3 實驗與結果分析

3.1 Mountain Car問題求解

3.1.1 實驗描述

為驗證本文算法的性能,將本文提出的基于二階TD誤差雙網絡DQN算法與原始DQN算法應用于經典控制Mountain Car問題進行比較。

Mountain Car問題示意圖如圖2所示,其中一輛車在一維軌道上,位于兩座“山”之間,即帶有坡面的谷底,目標是把車開到右邊的山上(圖2中小旗的位置)。然而,小車由于動力不足,不能一次通過山體,因此小車必須借助前后加速的慣性才能通過山頂。Mountain Car實驗的狀態是兩維的,其中一維表示位置,另一維表示速度。其中,小車的位置區間為[-1.2,0.6],速度的區間為[-0.07,0.07]。動作空間有3個離散動作,分別表示向左、向右、無動作。在情節開始時,給定小車一個隨機的位置和速度,然后在模擬環境中進行學習。當小車到達目標位置(圖2中小旗的位置)時,情節結束,并開始一個新的情節。

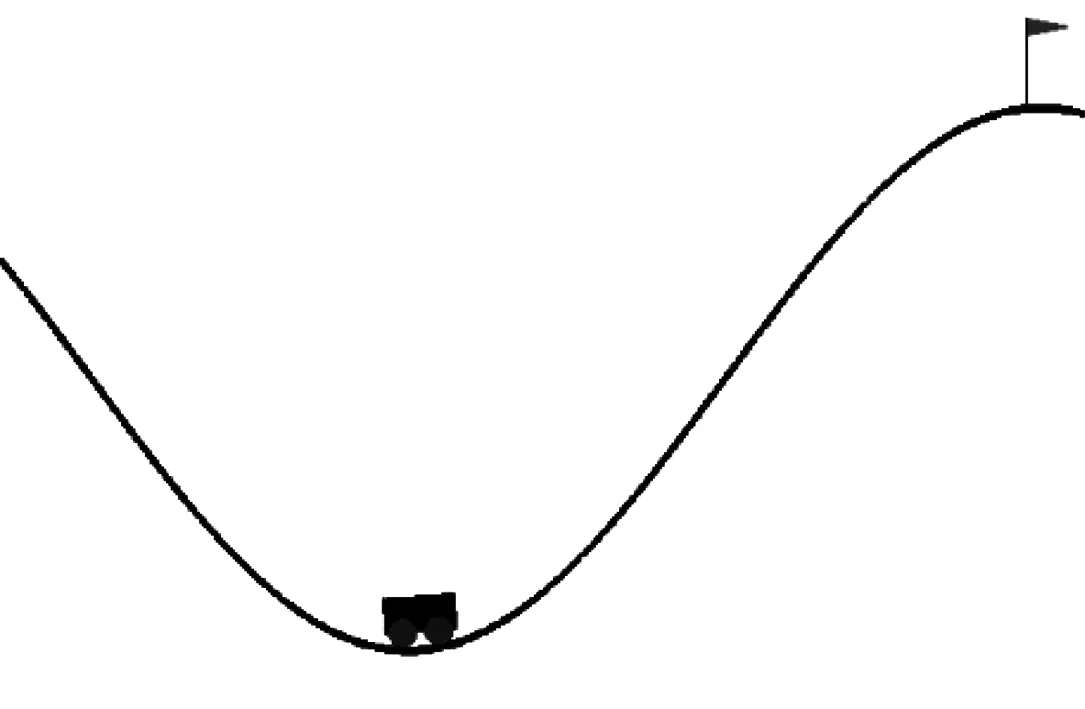
圖2 Mountain Car問題示意圖

當小車到達目標位置時,立即獎賞是1,其他情況下立即獎賞與位置有關。獎賞函數如式(13)所示:

(13)

3.1.2 實驗設置

本文的實驗環境是Open AI Gym,神經網絡參數的優化器是RMSprop,隱藏層使用的線性修正單元為ReLU。

實驗中的具體參數設置為:學習率β為0.001,ε-greedy策略中ε的值為0.9,其迭代的速率為0.000 2,迭代間隔為300,經驗池的數量為3 000,情節數量設置為500,訓練中mini-batch的值為32。

3.1.3 實驗分析

在α不同取值情況下,比較二階TD誤差雙網絡DQN算法和傳統DQN算法應用于Mountain Car問題的性能表現,如圖3所示(每個實驗執行500個獨立情節)。其中,α分別取值0.1、0.3、0.5和0.7。在實驗過程中,每個算法都被獨立執行20次,求出平均值。

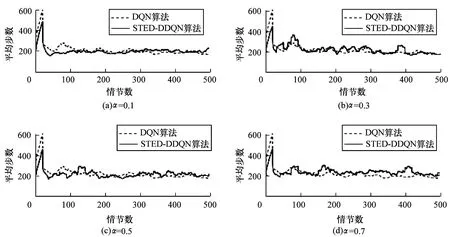
圖3 2種算法求解Mountain Car問題的性能對比

從圖3(a)可以看出,α取0.1時,在第40個情節處的平均步數降至最低,之后緩慢收斂至穩定值,第70個情節后穩定在200步左右。從圖3(b)可以看出,α取值為0.3時,算法在前400個情節的實驗過程中都有大幅度的振蕩,效果較差,第400個情節之后的性能與DQN算法性能相似。從圖3(c)可以看出,α取值為0.5時,二階TD誤差雙網絡DQN算法的實驗效果與DQN算法的收斂效果相似,符合上文的理論推導。從圖3(d)可以看出,當α取值為0.7時,算法的實驗效果在500個情節內有3個明顯的振蕩高峰,收斂效果變差。由此看出,α取值逐漸變大時,振蕩幅度變大,算法的收斂性能越差。這是由于雙網絡DQN算法在TD誤差的基礎上引入了二階TD的概念,使得算法能夠在兩個同構值函數網絡的學習基礎上進行新一輪的迭代學習,減小了算法模型的計算誤差,進一步提高了算法的收斂穩定性。因此,二階TD誤差雙網絡DQN算法的前期收斂速度比DQN更快,振蕩較少且更接近收斂值。綜上,當α取值為0.1時,算法的收斂效果最好。

圖4是在α=0.1的條件下,選取不同學習率β的算法效果對比。可以看出:β取0.001時,算法前20個情節學習的效果與其他取值情況相似,第20個～第70個情節時學習效果較好,第100個情節處有一個較大幅度的振蕩,第240個～第270個情節處有較高幅度的振蕩,之后算法逐漸穩定至收斂值;β取0.002時,前期學習效果較差,第50個～第120個情節時有較大幅度的振蕩,第120個～第500個情節時都有較小幅度的振蕩;β取0.005時,算法在第50個情節～第100個情節處有較小幅度的振蕩,之后的情節中有小幅度的振蕩,相比其他取值情況,收斂效果較好。因此,根據實驗結果與實驗分析,學習率β的值選擇0.005效果最好。由此看出,面對離散動作問題時,學習率并非越小越好,學習率的選擇需要根據具體問題分析。

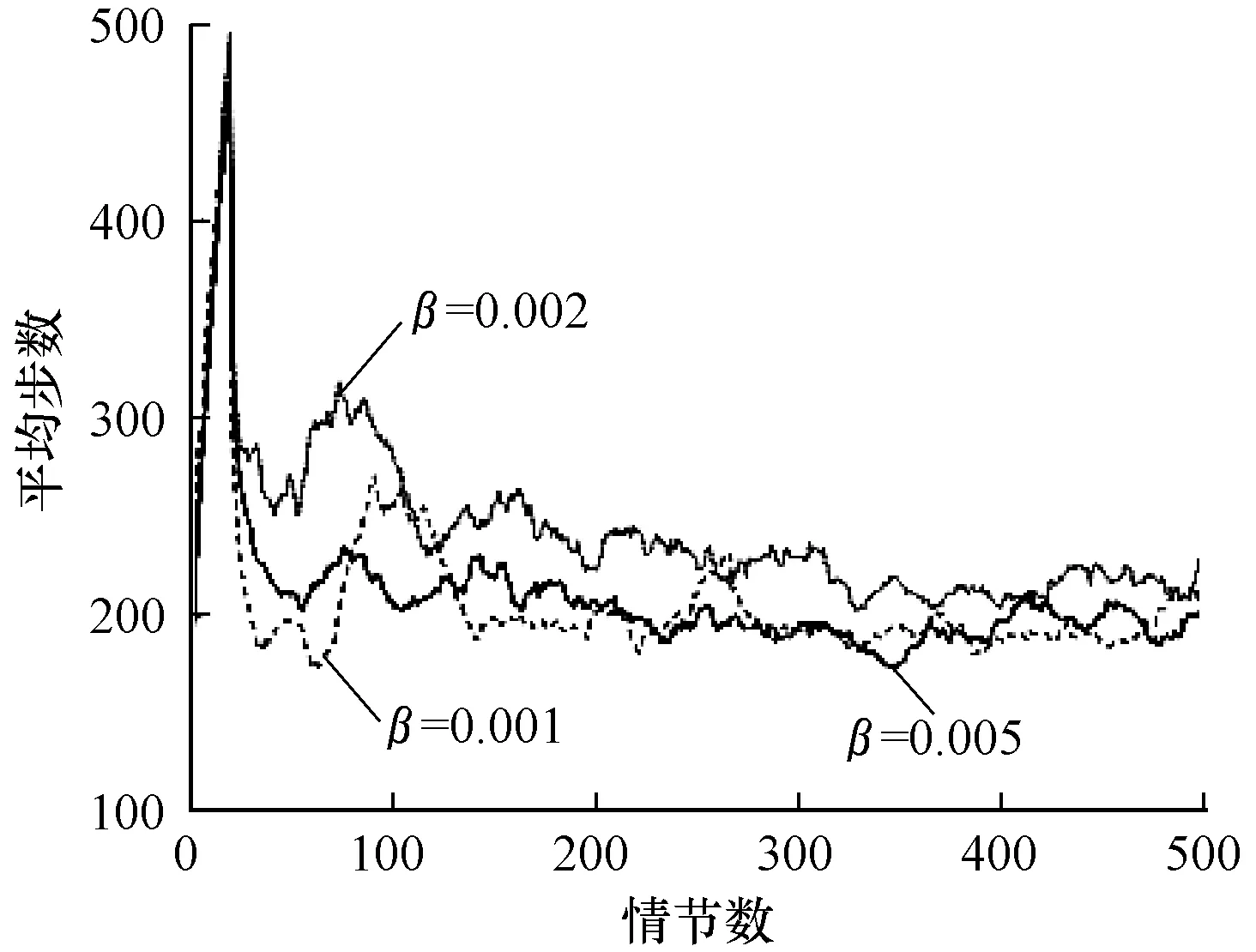
圖4 不同β取值下本文算法的學習性能

Fig.4 Learning performance of the proposed algorithm under differentβvalues

在學習率β取0.005且α=0.1的情況下,針對不同ε-greedy最大取值對學習效果的影響進行對比,如圖5所示,其中,ε的最大值分別取0.90、0.95以及0.99,且每次動作選擇后,每一次的迭代值為0.000 2。可以看出:ε最大值取0.90時,算法前期逐步收斂,收斂效果相比其他取值較好,第400個～第460個情節處有輕微振蕩;ε最大值取0.95時,算法前期振蕩明顯,第160個情節之后逐漸穩定至收斂值;ε最大值取0.99時,算法在前150個情節振蕩幅度巨大,之后的情節中振蕩幅度逐漸降低。原因是算法的前期需要積極探索更有效的策略,當ε取值較大時,前期每個情節探索最優動作的概率較大,經過多個情節,ε的值就會降低到最小,導致前100個情節震蕩幅度較大,難以收斂。因此,綜合上述分析,ε取值為0.9時效果最好。

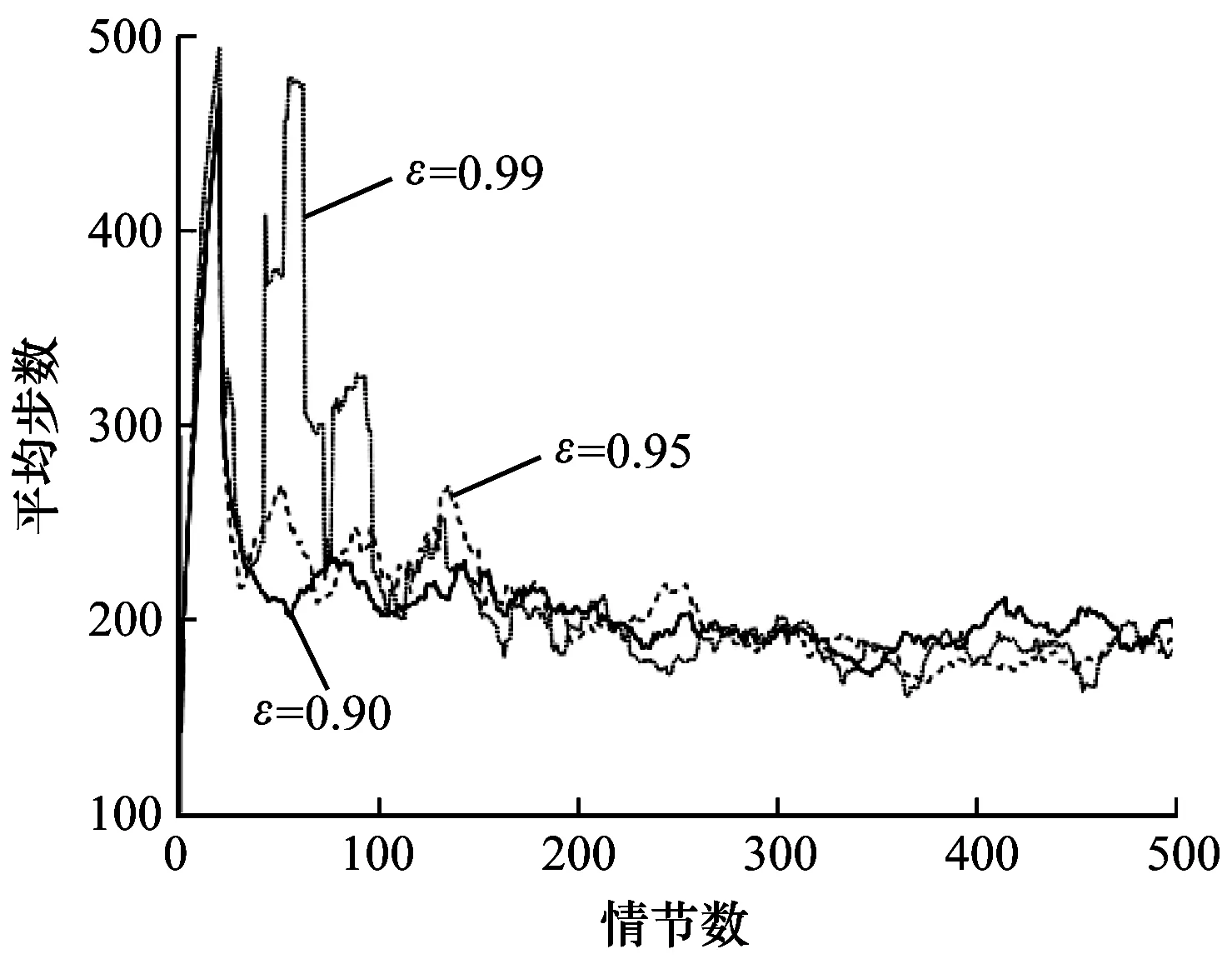
圖5 不同ε取值下本文算法求解Mountain Car問題的性能

Fig.5 Performance of solving Mountain Car problem by the proposed algorithm under differentεvalues

3.2 Cart Pole問題求解

3.2.1 實驗描述

為進一步驗證二階TD誤差雙網絡DQN算法的性能,將其與原始DQN算法應用于空間狀態更為復雜的平衡桿(Cart Pole)問題進行性能比較。

Cart Pole問題示意圖如圖6所示,其中一根桿由一個非驅動的接頭連接到一輛小車上,小車沿著無摩擦的軌道運行。

圖6 Cart Pole問題示意圖

該系統的狀態是四維的,可以表示為:Ssate={x,xdot,T,Tdot};動作是一維的,有2個離散動作:向左或向右。系統中通過施加一個+1或-1的力來控制小車,且當鐘擺處于直立狀態時,Agent的目標是阻止它倒下。當Agent控制操作桿走一步,且桿子保持垂直時,環境給予Agent一個立即獎賞,當桿子與垂直方向的角度超過15°,或者小車從中心移動超過2.4個單位時,游戲結束。為使獎賞函數更合理有效,設置獎賞函數如式(14)所示:

(14)

3.2.2 實驗設置

本文的實驗環境是Open AI Gym,神經網絡參數的優化器是RMSprop,隱藏層使用的線性修正單元為ReLU。

實驗中的具體參數設置為:學習率β為0.01,ε-greedy策略中ε的值為0.9,ε迭代的速率為0.001,迭代間隔N為100,經驗池的數量為2 000,情節數量設置為3 000,訓練中mini-batch的值為32。

3.2.3 實驗分析

在α不同取值情況下,比較二階TD誤差雙網絡DQN算法和傳統DQN算法應用于經典Cart Pole問題的性能表現,如圖7所示(實驗中每個算法都獨立執行3 000個情節)。針對α的取值設計實驗,驗證算法的收斂性能與α值設置的關聯性,其中,α分別取值0.1、0.3、0.5和0.7。

圖7 2種算法求解Cart Pole問題的性能對比

從圖7可以看出,原始DQN算法約在第60個情節處開始學習,到750個情節時趨于穩定值400,在之后的情節中仍有較高幅度的振蕩,并且算法在第2 000個情節左右獲得最低獎賞值。從圖7(a)可以看出,α取0.1時,二階TD誤差雙網絡DQN算法也在60個情節左右開始學習,在第250個情節處接近穩定值500,之后的情節中有輕微振蕩,第1 800個～第2 000個情節時有較大波動,最終能夠穩定收斂并且取得比DQN算法更高的獎賞值。從圖7(b)可以看出,α取0.3時,二階TD誤差雙網絡DQN算法在第250個～第1 700個情節性能表現較好,之后的情節中振蕩較大,收斂性能較差。從圖7(c)可以看出,α取0.5時,算法的收斂性能與DQN算法相似,滿足上文的理論推導。從圖7(d)可以看出,α取0.7時,算法的振蕩幅度較大,沒有明顯的收斂表現。通過對比分析可以得出結論:當α取0.1時,算法的收斂效果最好,穩定性最強。比較不同取值情況下α的取值可知,STDE-DDQN算法由于引入二階TD誤差,其通過相同值函數網絡的迭代學習可降低模型的學習誤差,具有更好的收斂穩定性。

圖8是二階TD誤差雙網絡DQN算法在α取0.1時不同學習率下的收斂效果對比,其中分別設置學習率β為0.01、0.005以及0.002。可以看出:β取0.01時,在第250個情節時開始收斂,收斂穩定值為520,第1 750個～第2 000個情節處收斂性能下降,之后在收斂值附近振蕩,且振蕩幅度較大;β取0.005時,與其他取值情況相比,前期收斂較慢,且在收斂值左右振蕩,從第300個情節處開始,一直在收斂值左右輕微振蕩,整體性能表現較好;β取0.002時,算法學習率較低,學習緩慢,但初期學習效果較好,第200個情節處開始收斂,在第2 000個～3 000個情節處算法的振蕩幅度較大,收斂效果較差。由此可知:當學習率較大時,算法收斂較快,但振蕩幅度較大,容易陷入局部最優的問題,難以收斂;當學習率較小時,學習效果較好,但算法學習速率較慢,收斂情況不穩定。因此,綜合上述分析,學習率β的值選擇為0.005時,算法的性能最好。

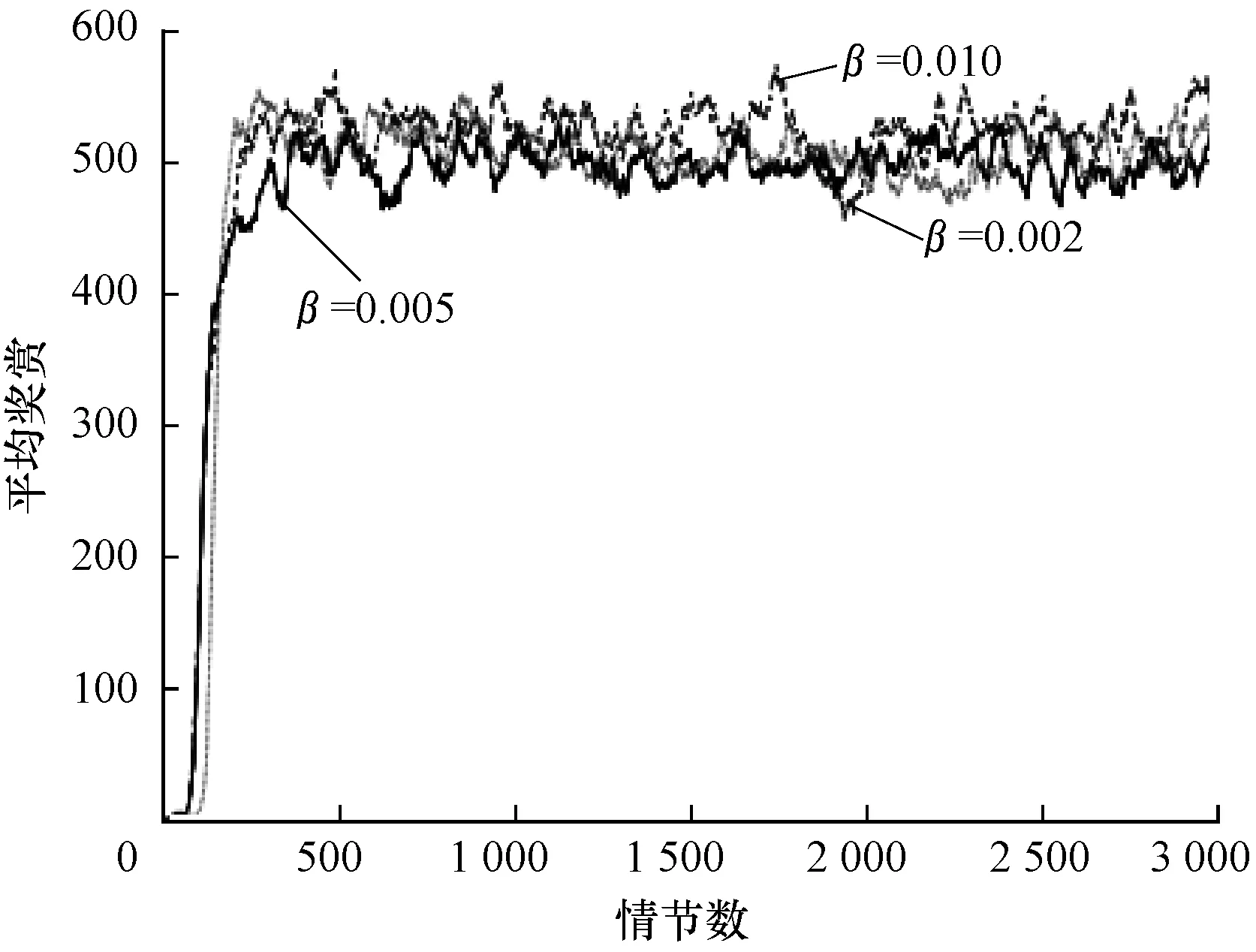
圖8 不同β取值下本文算法求解Cart Pole問題的性能

Fig.8 Performance of solving Cart Pole problem by the proposed algorithm under differentβvalues

圖9是在保證α與學習率β的情況下,選取不同ε-greedy策略二階TD誤差雙網絡DQN算法的收斂效果對比。可以看出:ε取0.90時,算法收斂較慢,在第400個情節處開始收斂,并在之后的情節中一直以較小的振蕩幅度維持在收斂穩定值左右;ε取0.95時,算法在第300個情節處開始收斂,且收斂速度較快,振蕩幅度較小;ε取0.99時,算法的平均獎賞較高,達到650左右,但是算法不易收斂,振蕩幅度較大,原因是ε-greedy策略取值較大,前期Agent探索概率大,易找到最優策略與最優值,但后期動作選擇時,ε的值過小,缺少探索,不易收斂。因此,ε取值為0.95時效果最好。

圖9 不同ε取值下本文算法求解Cart Pole問題的性能

Fig.9 Performance of solving Cart Pole problem by the proposed algorithm under differentεvalues

4 結束語

本文通過引入N階TD誤差的概念,提出一種基于二階TD誤差的雙網絡DQN算法。構建兩個同構的值函數網絡分別表示先后兩輪的值函數,并重構損失函數,使Agent能夠在先后兩輪值函數的基礎上進行學習,減小學習誤差,提高算法的收斂穩定性。此外,還通過對比實驗探索收斂效果更好的參數取值。基于Gym實驗平臺的Mountain Car和Cart Pole求解實驗結果表明,該算法能夠有效提高值函數估計的穩定性,具有較好的收斂性能。本文工作通過引入二階TD誤差設計改進的DQN算法,下一步將針對更高階的情況對算法收斂性能進行優化。