巖石黏性系數的超聲波法測試與敏感性分析

孟世明，管華棟，王觀石

(江西理工大學建筑與測繪工程學院，江西 贛州 341000)

1 巖石黏性系數測試的意義與現狀

巖石的黏性系數反映了在一定載荷下，巖石變形與時間相關的特性，是表征巖石黏彈性質的重要參數之一[1-2]。進行自然界的地震分析和工程中的爆炸應力波傳播規律研究時，都需要借助巖石的黏彈性本構模型，而巖石的黏性系數的取值是否合理，直接影響計算分析的正確性。因此，巖石黏性系數的準確獲取和深入分析有助于巖石黏彈性模型研究，進而更好地開展巖石動力學特性研究，為地下深部巖土工程的設計和施工提供參考。

目前，巖石黏性系數測試主要有懸臂梁彎曲共振法[3-4]和動態機械分析法[5]。鄧科濤等[6]基于黏彈性材料在變形過程中有能量損耗的性質，采用加載周期三角波的方法建立了室內Maxwell模型的黏性系數測試方法；李魁彬等[7]基于材料參數與梁應變響應周期及振幅衰減的關系，提出了室內Kelvin模型的黏性系數測試方法。這些室內測試方法，由于條件所限，不利于推廣，更無法實現現場原位測試。巖石具有黏彈性，應力波在巖石中傳播會出現振幅衰減的現象[8-9]；王觀石等[10]基于應力波衰減規律，通過計算振幅的衰減系數，獲得了巖體的黏性系數，實現了巖體黏性系數的應力波原位測試。但應力波測試方法無法固定應力波的頻率，因而很難進行黏性系數隨頻率變化的研究。此外，現有研究成果中很少涉及到黏性系數對巖石密度、波速、彈性模量的相關性研究。

超聲波激發的頻率可控，便于重復試驗，測試簡單方便，既適用于室內測試，又適用于原位測試。為此，本文基于超聲波在Kelvin-Voigt黏彈體的衰減規律，提出了由超聲波幅值衰減規律來獲取黏性系數的超聲測試方法，開展了巖石黏性系數對密度、波速、彈性模量的相關性分析，并進行了巖石黏性系數隨發射波頻率的變化規律研究，研究成果可以為巖體力學參數測試和巖體動力學特性研究提供參考。

2 基于Kelvin-Voigt黏彈性體的巖石超聲波衰減模型

巖石實際是一種黏彈性介質，通常可以用Kelvin-Voigt模型描述其本構關系。因此把巖石抽象為各向同性的Kelvin-Voigt黏彈性體，假設巖石中超聲波沿X軸方向傳播，其一維波動方程見式(1)。

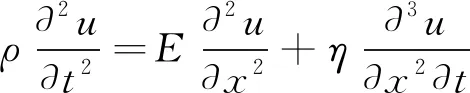
(1)

式中：u為巖石X軸方向的位移，m；t為時間，s；ρ為巖石密度，kg/m3；E為巖石彈性模量，GPa；η為巖石黏性系數，MPa·s。

若考慮超聲波隨空間衰減，則可假設任意t時刻的波形曲線，計算見式(2)。

u(x,t)=A0e-αxsin(ωt-kx)

(2)

式中：A0為初始振幅，m；α為衰減系數，m-1；ω為超聲波發射頻率，kHz；k為巖石中超聲波的響應波數，m-1。

把式(2)代入式(1)可得式(3)。

(2ωηαk+Ek2-Eα2-ρω2)sin(ωt-kx)=

(ωηα2+2Eαk-ωηk2)cos(ωt-kx)

(3)

要使式(3)成立，只需滿足正弦函數和余弦函數的系數為0，具體計算見式(4)。

(4)

解式(4)的二元二次方程組，并注意衰減系數α和波數k大于0，具體計算見式(5)。

(5)

進行巖石超聲波測試后，可以提取超聲波發射波的最大電壓輻值和接收波的最大電壓幅值，不同發射波頻率下的衰減系數計算見式(6)。

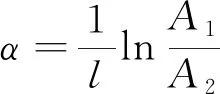
(6)

式中：A1為超聲波在巖樣發射端的最大電壓幅值，V；A2為超聲波在巖樣透射端的最大電壓幅值，V；l為巖樣試件的長度，m。

聯立式(5)和式(6)，可得Kelvin-Voigt黏彈性體的黏性系數，計算見式(7)。

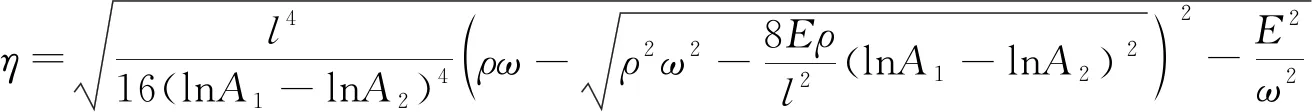
(7)

因此，通過巖石超聲波試驗，得到不同發射波頻率下的發射波和接收波最大幅值，再把巖石的長度、密度以及彈性模量代入式(7)即可求得基于Kelvin-Voigt黏彈性體的巖石黏性系數。

3 巖石超聲波試驗

巖石超聲波測試采用的測試系統包括：固緯AFG-3000任意波形信號發生器、固緯GDS-2000A數字存儲示波器、HA-405高壓放大器、汕頭超聲生產的50K-P40F聲波換能器，以及高靈敏度聲波信號接收器和穩壓電源。通過波形信號發生器改變超聲波發射頻率，分別進行20 kHz、25 kHz、30 kHz、35 kHz、40 kHz、45 kHz、50 kHz的巖樣超聲波波形測試，保存并導出波形數據。

試驗選用的3個巖樣均取自福建省某礦山，巖樣物理力學參數見表1，其中巖樣的彈性模量是在超聲波測試完成后由單軸壓縮試驗測得。3個巖樣的密度、橫波波速和彈性模量都是遞增的，縱橫波波速比是遞減的，而縱波波速的變化沒有規律。

4 巖石黏性系數測試結果及敏感性分析

3個巖樣在20 kHz和50 kHz頻率下的超聲波發射波和接收波波形如圖1所示。3個巖樣的發射波波形幾乎相同，接收波受巖樣密度、彈性模量和黏性系數等參數影響，波形差異明顯。發射波頻率為20 kHz時，3個巖樣接收波的最大幅值分別為0.43 V、0.38 V和0.35 V；發射波頻率為50 kHz時，3個巖樣接收波的最大幅值分別為0.24 V、0.16 V和0.2 V。同一個巖樣的接收波隨發射波頻率增加而大幅度衰減，符合應力波在巖石中頻率越高衰減越快的傳播規律。

表1 巖樣參數

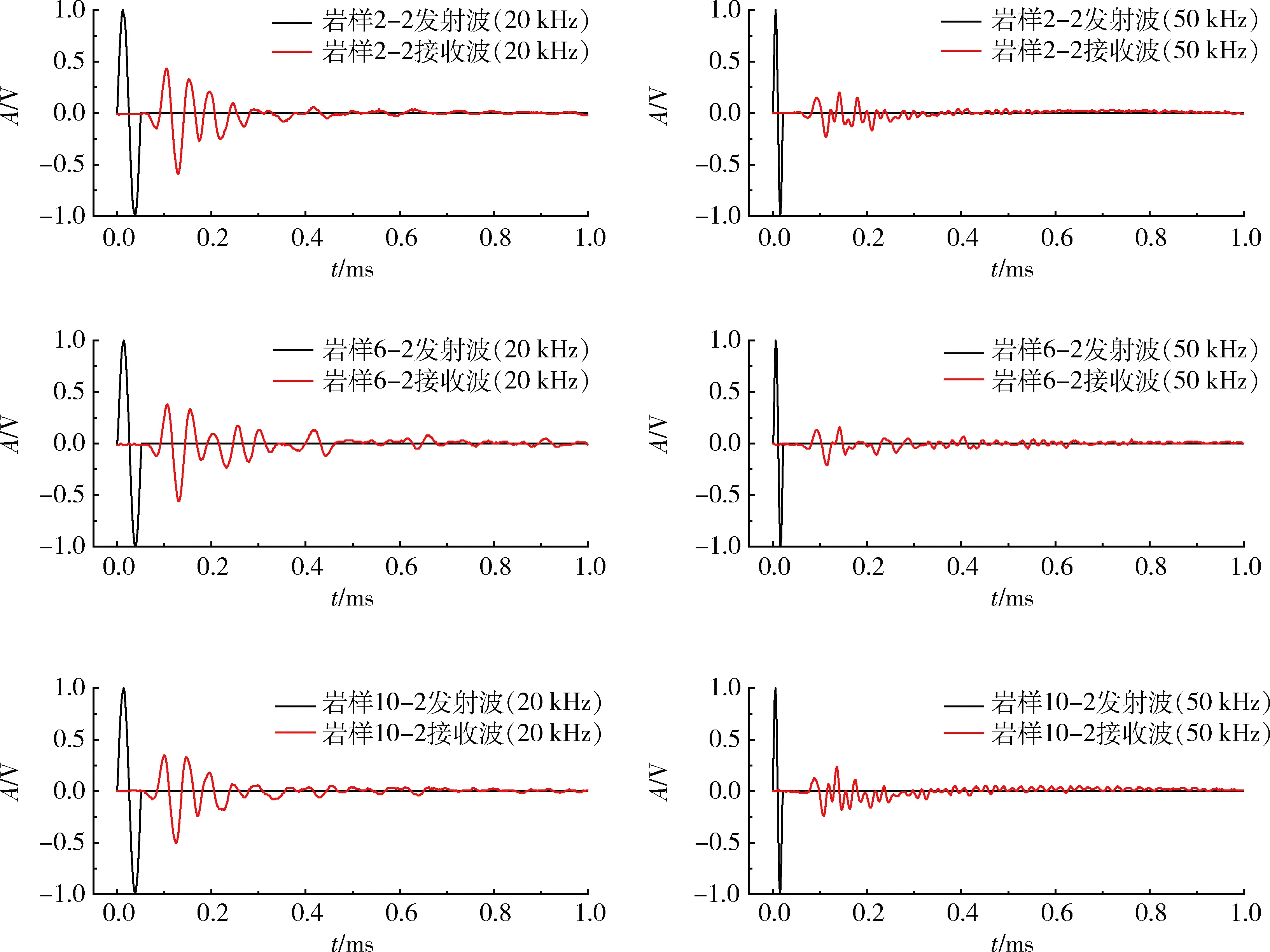
圖1 3個巖樣在不同頻率下的超聲波波形

Fig.1 Ultrasound waveform of three rock specimens at different frequencies

根據超聲波測試記錄的波形數據，提取發射波的最大電壓輻值和透射波的最大電壓幅值，再利用式(7)計算不同發射波頻率下的黏性系數，計算結果見表2。

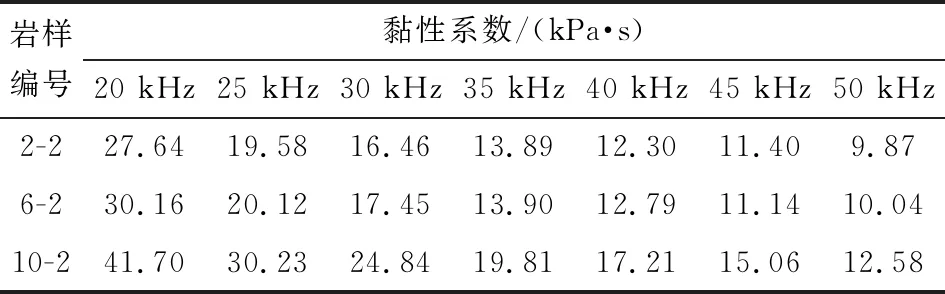
表2 不同發射波頻率下的黏性系數

1) 巖樣黏性系數與密度、波速及彈性模量的相關性分析。表2中，同一個發射波頻率下(除45 kHz外)，巖樣2-2的黏性系數最小，巖樣6-2次之，巖樣10-2最大，這與巖樣密度、橫波波速、彈性模量的大小排序相同，而與巖樣縱橫波波速比的大小排序相反；3個巖樣的縱波波速變化沒有規律，因此不進行黏性系數與縱波波速之間的變化分析。分別計算3個巖樣從發射波頻率為20 kHz到50 kHz的黏性系數減小率，巖樣2-2為64.2%，巖樣6-2為66.7%，巖樣10-2為69.8%，巖樣黏性系數的減小率與巖樣密度、橫波波速、彈性模量的大小排序相同，與巖樣縱橫波波速比的大小排序相反，即呈現與黏性系數相似的規律。

為了更好地分析巖樣黏性系數與密度、波速及彈性模量的相關性，引入相關系數，計算見式(8)。相關系數為正，表示兩個參數為正相關，反之則為負相關；相關系數的絕對值越大，說明兩個參數相關性越強，對其變化也越敏感。

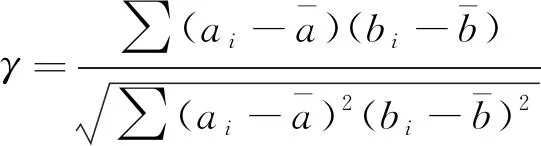
(8)

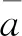
利用式(8)分別計算不同發射波頻率下巖樣的黏性系數與其密度、波速、彈性模量的相關系數，結果見表3。

由表3可知，不同發射波頻率下巖樣的黏性系數與彈性模量的相關系數最大，為0.985～1，屬于正相關；不同發射波頻率下巖樣的黏性系數與縱橫波速比的相關系數次之，為-0.818～-0.927，屬于負相關；不同發射波頻率下巖樣的黏性系數與密度和橫波波速的相關系數較為接近，都為正相關；不同發射波頻率下巖樣的黏性系數與縱波波速的相關系數最小，為-0.215～0.012，除發射波頻率20 kHz外都表現為負相關；因此，綜合分析表明：同一發射波頻率下，巖樣的黏性系數對彈性模量的變化最為敏感，而對縱波波速的變化最不敏感，可以用彈性模量的變化來估算黏性系數的變化。

此外，分別計算巖樣從發射波頻率為20 kHz到50 kHz的黏性系數減小率與各參數的相關性系數，發現：黏性系數隨頻率的減小率與縱橫波速比的相關系數最大， 相關系數為-0.996，屬于負相關；其次是彈性模量， 其相關系數為0.940， 屬于正相關； 最小為縱波波速， 其相關系數為0.300，也屬于正相關。

表3 不同發射波頻率下巖樣的黏性系數與各參數的相關性分析

2) 巖樣黏性系數擬合參數與密度、波速及彈性模量的相關性分析。不同發射波頻率之間相互比較，發射波頻率為20 kHz時巖樣的黏性系數最大，發射波頻率為50 kHz時巖樣黏性系數最小，即巖樣的黏性系數與發射波頻率呈負相關。分別繪制不同巖樣黏性系數隨超聲波發射頻率變化的散點圖，并用負指數擬合，如圖2～4所示。

由圖2～4可知，可以把3個巖樣的擬合公式可以統一為式(9)。

η=C1e-C2ω

(9)

式中：C1為擬合參數，kPa·s；C2為擬合參數，μs。

利用式(8)分別計算3個巖樣的擬合參數與其密度、縱橫波波速、彈性模量的相關系數，結果見表4。

由表4可知，巖樣黏性系數的擬合參數C1與彈性模量相關系數最大，為0.995，屬于正相關；C1與縱橫波速比的相關系數次之，為-0.942，屬于負相關；C1與縱波波速的相關系數最小，為0.053；擬合參數C1對彈性模量的變化最為敏感，而對縱波波速的變化最不敏感，可以用彈性模量的變化來估算C1。巖樣黏性系數的擬合參數C2與縱橫波波速比的相關系數最大，為-0.996，屬于負相關；C2與橫波波速和密度的相關系數較為接近， 都大于C2與彈性模量的相關系數， 都屬于正相關；C2與縱波波速的相關性最小，為0.463；擬合參數C2對縱橫波波速比的變化最為敏感，而對縱波波速的變化最不敏感，可以用縱橫波波速比的變化來估算C2。

圖2 巖樣2-2不同發射波頻率下的黏性系數

Fig.2 Viscous coefficient of rock specimen 2-2 at different incident wave frequencies

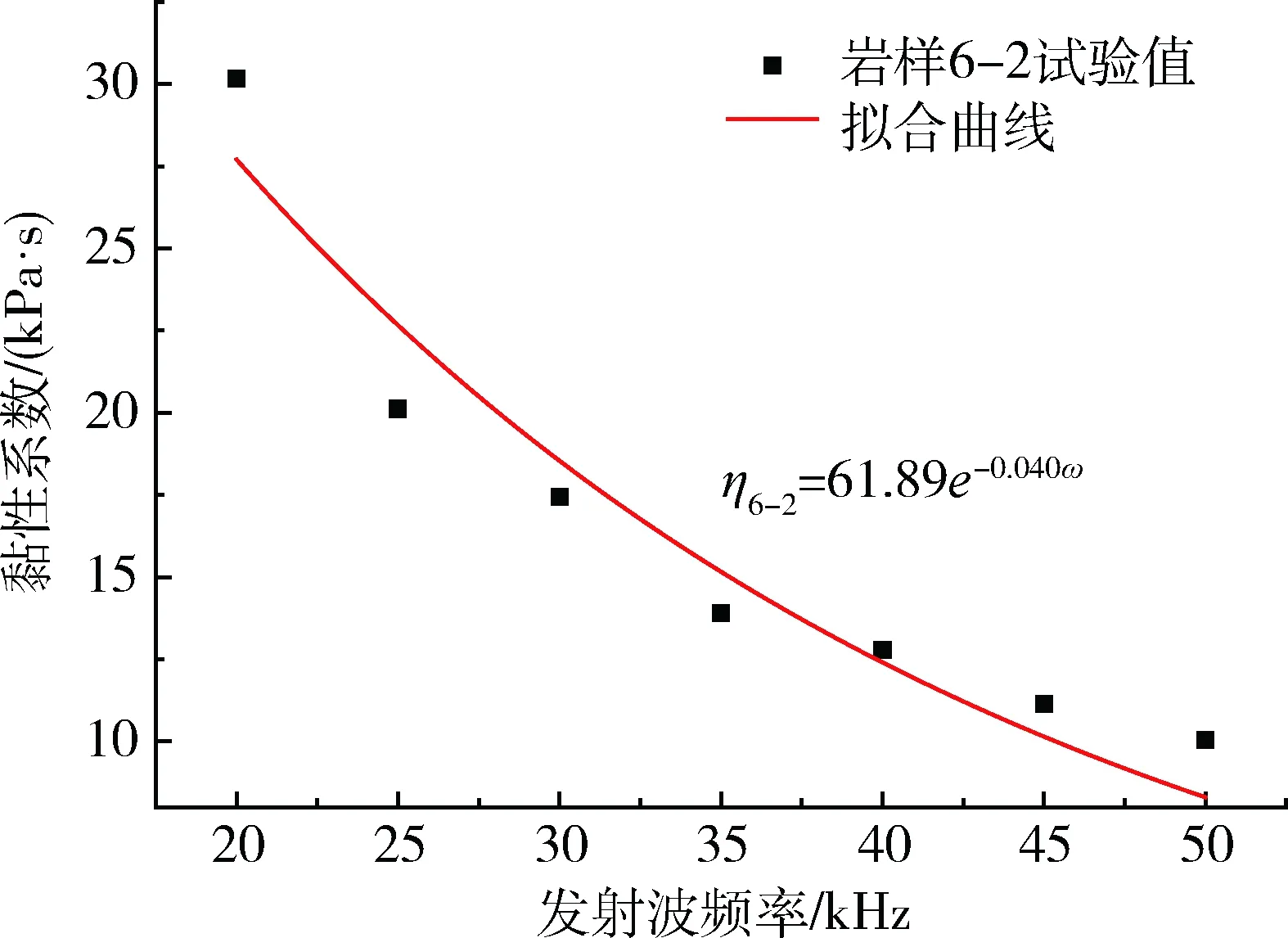
圖3 巖樣6-2不同發射波頻率下的黏性系數

Fig.3 Viscous coefficient of rock specimen 6-2 at different incident wave frequencies

圖4 巖樣10-2不同發射波頻率下的黏性系數

Fig.4 Viscous coefficient of rock specimen 10-2 at different incident wave frequencies

表4 巖樣黏性系數的擬合參數的相關性分析

5 結 論

1) 本文推導了Kelvin-Voigt黏彈性體的黏性系數計算公式見，從而可通過密度、彈性模量、頻率以及超聲波發射波、接收波幅值確定巖石的黏性系數。

2) 通過巖石超聲波試驗，獲得了7種發射波頻率下的巖石黏性系數，巖石黏性系數是非定常的，會隨發射波頻率的變化而變化。

3) 巖石黏性系數與其密度、縱橫波波速、彈性模量呈正相關，與其波速比呈負相關，巖石黏性系數對彈性模量的變化最為敏感，而對縱波波速的變化最不敏感，可以用彈性模量的變化來估算黏性系數。

4) 巖石黏性系數與發射波頻率近似呈負指數函數關系，擬合關系式可以統一用式(9)表示，擬合參數C1對彈性模量的變化最為敏感，而對縱波波速的變化最不敏感，擬合參數C2對縱橫波波速比的變化最為敏感，而對縱波波速的變化最不敏感。

致謝衷心感謝國家自然科學基金項目(編號：41462009)和江西理工大學人才培養項目(編號：3401223395)對本文試驗的資助，特別感謝同行專家孫利輝副教授對本文公式的運算過程和運算結果所做的審查糾正工作。