基于時間觸發通信的機載網絡可靠性

馬 躍，朱紀洪，楊佳利

(清華大學 計算機科學與技術系，北京 100084)

0 引 言

隨著航空電子技術的不斷發展，航空電子系統架構經歷了從早期的聯合式向綜合模塊化(integrated modular avio-nics，IMA)以及最新的分布式綜合模塊化(distributed integrated modular avionics，DIMA)發展的過程[1]。DIMA在IMA的基礎上，將綜合模塊分布式放置，具有分布計算、可擴充、便于維修等諸多優點，同時降低了系統重量、體積和復雜性，是未來航空電子系統架構的發展方向。

分布式架構對機載網絡的帶寬、實時性和可靠性提出了更高要求，以1553B總線為代表的傳統機載網絡存在通信速率低、過度依賴總線控制器和故障隔離困難等問題，難以滿足DIMA的發展需求。奧地利的Kopetz教授根據時間觸發機制，提出時間觸發協議(time-triggered protocol，TTP)，后推廣至交換式網絡中，提出了時間觸發以太網(time-triggered Ethernet，TTE)技術。TTE具有確定性、高可靠、低延遲等特點，能夠滿足分布式航空電子系統高速率、高可靠和故障隔離的要求，適應未來DIMA的發展需求[2]。

航空電子系統通信網絡的可靠性不僅關乎各種飛行控制指令的完成，更關系到飛行器本身的安全。本文分析了TTE在航電系統應用的可靠性問題，并探討通過余度設計增強系統可靠性。貝葉斯網絡是一種概率圖型模型，在不確定知識表達和推理領域有著廣泛應用，本文將使用貝葉斯網絡模型分析TTE網絡的可靠性。

1 機載通信網絡特性和需求

相比于普通以太網，機載網絡有拓撲和規模固定、通信任務周期性強、通信任務需求明確等特性，而航空電子系統架構的發展也對機載組網提出了更高的要求。本章對機載網絡的兩種通信機制：事件觸發機制和時間觸發機制進行了對比，總結了兩種機制在機載網絡通信的優缺點，分析了未來DIMA架構通信網絡的發展方向。

1.1 機載網絡通信系統技術特性

根據航空電子設備的工作特點和需求，機載網絡通信系統主要有以下技術特性。

1.1.1 網絡拓撲和規模固定

飛行器一旦研制成型后，其電子設備的數量和位置相對固定，通信網絡的拓撲結構一般不會改變，無需考慮設備接入帶來的網絡規模變化問題。

1.1.2 通信任務周期性強

飛行器的航空電子設備主要包括核心處理機、信息采集系統、遠程通信系統和發動機及作動系統等，各系統之間的工作有明確的邏輯順序。由于飛行器大多采用周期性采樣與控制方式，所以電子設備各系統之間的通信任務也存在明顯的周期性，且通信周期基本固定不變。

1.1.3 通信任務需求明確

為保證飛行任務的安全可靠，飛行器設計時要對通信任務需求進行分析計算。一般情況下，飛行過程中各子系統的通信任務需求不會發生變化，不會出現臨時增加通信任務的情況。

1.2 DIMA系統的組網需求

機載網絡作為航空電子系統的互連通道，對整個系統的性能有著重要影響。DIMA對機載網絡提出了更高的要求，主要體現在帶寬、實時性和可靠性等方面。

1.2.1 帶寬

機載網絡的帶寬需求取決于航空電子各子系統的集成綜合程度。早期的聯合式架構中，各子系統獨立完成信息處理，子系統之間的交互性較弱，對帶寬要求比較低。在DIMA系統中，數據計算任務分布在各個子系統，需要通過機載網絡共享中間計算結果，使得網絡的帶寬需求大大增加。

1.2.2 實時性

實時性表征了系統在規定的時間間隔內完成預定目標的能力，一般用任務的最壞響應時間與截止期限對比。航空電子系統是安全關鍵實時系統，作為系統的信息互連通道，機載網絡必須保證數據的傳輸滿足實時性要求。

1.2.3 可靠性

可靠性的定義請參見文獻[3]，其主要表征了產品在規定的時間和條件下，完成規定功能的能力。

系統可靠性指標是對系統可靠性要求的定量規定，可靠性的規定有4種基本方法：平均壽命、任務可靠度、成功概率和故障率。平均壽命指不可修復產品發生失效情況前工作時間的平均值或可修復產品兩次相鄰故障間工作時間的平均值；任務可靠度指在規定任務時間內的正常工作概率，反映了產品在規定任務時間內完成要求功能的能力；成功概率適用于規定一次使用裝置的可靠性(與時間無關)；故障率指規定時間內的故障率，適用于長壽命或故障率很小的產品的可靠性。航空電子系統通信網絡可靠性可使用故障率作為指標度量。

飛行器對航空電子系統的可靠性和容錯能力要求極高，機載網絡作為航空電子系統重要組成部分，其可靠性對飛行器的可靠性有著重要影響。網絡可靠性主要包括路徑連通可靠性和信息流通可靠性[4]，前者主要依賴于硬件基本可靠性，而后者關注網絡服務的可靠性。TTE通信是由通信任務調度表驅動，可以避免網絡流量擁堵并具有確定的延遲[5]，在信息流通可靠性方面有著天然的優勢。

1.3 消息觸發機制

傳統的機載通信網絡，如1553B總線、CAN總線、AFDX等，均采用事件觸發機制的通信方式，即當通信節點有通信需求時，盡快將消息發送至通信鏈路中。事件觸發機制有靈活性高、按需分配、節省鏈路資源等優勢。但當鏈路負擔過重時，事件觸發機制的通信性能嚴重下降。此外，高靈活性通常意味著不確定性，由此會帶來故障檢測和隔離的難度增加。

時間觸發機制指在統一的時間基準下，根據一個預先安排的時間調度表進行數據傳輸和交換[6]，可以避免事件觸發機制中潛在的消息沖突問題，不會出現因為排隊而導致的不確定性問題，顯著提高網絡資源利用率。此外，時間觸發機制的確定性也增強了故障檢測和隔離的能力。總體來看，時間觸發機制具有實時性高、可靠性強和可預測等優勢，但上述優勢是以犧牲靈活性為代價的，因此在機載網絡中，需要綜合考慮靈活性、確定性和可靠性等因素。

事件觸發機制與時間觸發機制的對比見表1。結合機載網絡通信系統的技術特性，可采用時間觸發機制來保證系統的實時性、確定性和可靠性，為DIMA架構的發展提供支撐。

2 TTE在航空電子系統中的應用

美國汽車工程師學會(society of automotive engineers，SAE)于2011年發布了SAE AS6802時間觸發以太網標準，AS6802在標準以太網基礎上規定可用于時間觸發通信的同步協議，具有確定性、高可靠性和高帶寬利用率等特點，可有效滿足航空電子安全關鍵系統的應用需求。

表1 事件觸發機制與時間觸發機制對比

2.1 TTE的研究現狀

近年來，TTE技術已經得到許多制造企業的重視，國外航空航天、車載控制、工程機械等領域已出現TTE產品的應用。NASA將TTE作為部分航天系統主干網，成功應用到其獵戶座多用途載人飛船中。歐洲宇航局也計劃在其重型運載火箭中應用TTE網絡構建實時信息系統。

2.2 TTE在航空電子系統應用的優勢

航空電子系統的高度綜合化，對航空電子網絡的性能提出了更高的要求。航空電子網絡負責航空電子系統各子系統之間的相互通信，必須具有可靠性、實時性和開放性等特性，這些需求與TTE的特性完全契合，主要體現在以下幾方面。

2.2.1 系統集成和擴展

TTE可以在保證TT消息最高優先級的基礎上兼容ET消息，實現相對靈活的信息處理方式[7]。TTE集群內的所有終端和交換機具有相同的同步優先級，不同集群可獨立運作，多個集群可以進一步構成更大的集群網絡，方便系統擴展。

2.2.2 消息傳遞確定性

TTE內各通信節點在全局統一時間基準下，通過離線調度表，使TT消息具有完全的時間確定性。TTE的最小化延遲和消息傳輸可確定性，可以滿足系統的傳輸確定性要求[8]。同時，得益于完全的確定性，相比傳統以太網，TTE可以提高網絡帶寬資源利用率。

2.2.3 容錯策略和故障隔離

TTE的通信具有良好的可預測性，便于系統快速發現故障問題，減少故障判定時間[9]。TTE的容錯策略可以使系統所有正確節點對哪些是錯誤節點達成一致，對故障節點進行隔離，消除誤差傳播[10]，盡量避免由于單個節點的失效導致系統失效的情況，方便系統重新配置和恢復。

3 可靠性分析

航空電子系統的可靠性要求極高，要求一定時間范圍內系統的失效概率低至可以忽略的程度[11]。本章將探討航空電子系統通信網絡可靠性研究方法，重點分析貝葉斯網絡在可靠性分析中的應用。

3.1 可靠性分析方法

可靠性分析方法的研究經過了多年的發展，總體來說，主要有數學模型法、上下限法、蒙特卡洛法等，其中，數學模型法根據系統各個部件的可靠概率，通過概率模型，應用狀態枚舉、容斥原理、圖形拓撲等方法，計算系統的可靠性概率。故障樹分析(fault tree analysis，FTA)方法是數學模型法的一種，它以系統最不期望發生的事件(稱頂事件)作為分析的目標，根據系統內可能發生的部件失效與頂事件之間的邏輯關系，用倒立樹狀因果關系圖形表示出來。

FTA在可靠性分析方面有著諸多優勢，如結構清晰、使用靈活等，但也存在著一些缺陷和不足，一是FTA只能解決二態性器件組成系統的可靠性問題；二是FTA只能解決器件之間的靜態邏輯組合關系，無法解決動態系統的各部件間的順序邏輯關系構成的故障分析問題。貝葉斯網絡具備了描述事件多態性和動態性邏輯關系的能力[12]，因此，基于貝葉斯網絡的故障樹模型，可較好地解決上述問題。

3.2 貝葉斯網絡

貝葉斯網絡是一個由節點和連接節點的有向邊組成的有向無環圖，圖中的節點代表隨機變量，邊代表隨機變量之間的相互依賴關系[13]。每個節點都附有各自的概率分布，其中根節點所附的是先驗分布，非根節點X所附的是X的條件概率分布Pr{X|pa(X)}，其中pa(X)為X的所有父節點的集合。

有向圖蘊含了條件獨立性假設，貝葉斯網絡中所有變量 {X1,X2,…,Xn} 的聯合概率分布表示為

(1)

貝葉斯網絡的顯式表示及其蘊含的條件獨立假設降低了模型概率的復雜度，為概率推理提供了很大的方便。同時，利用貝葉斯網絡還能得到更加豐富的信息，比如當故障發生時，可推測導致故障發生的最有可能的原因。

3.3 故障樹轉化為貝葉斯網絡

從故障樹和貝葉斯網絡的原理來看，貝葉斯網絡中的節點一一對應于故障樹中的事件，因此可以根據故障樹中事件的邏輯關系，建立貝葉斯網絡的依賴關系。以故障樹中的邏輯與門為例，說明故障樹向貝葉斯網絡轉化的方法。與門表示當兩個底事件都發生時，頂事件才發生的情況，頂事件T與底事件A、B間的概率關系為

Pr(T=1|A=1,B=1)=1,Pr(T=1|else)=0.

(2)

其轉化關系如圖1所示。

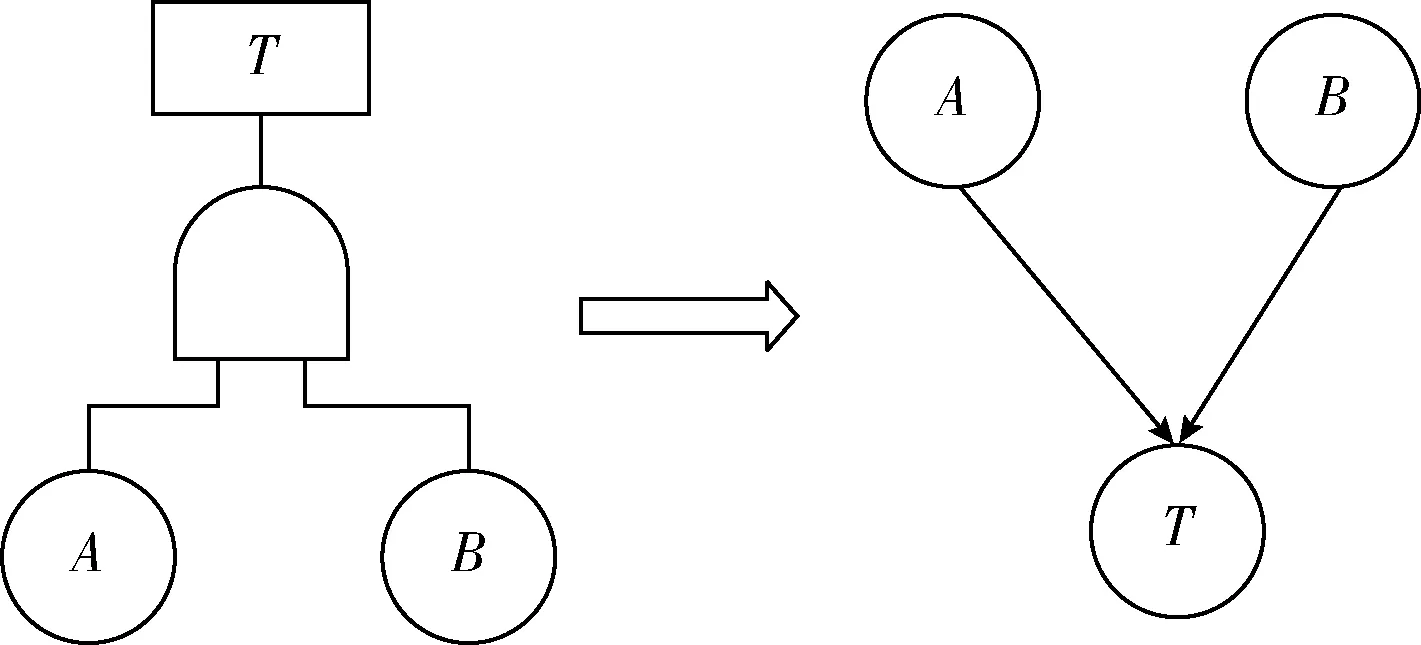
圖1 邏輯與門轉化為貝葉斯網

類似的，還可以將或門、非門、k/n門等故障樹中的邏輯門轉化為貝葉斯網的依賴關系，從而將故障樹轉化為貝葉斯網絡。

4 TTE網絡可靠性分析

本章，我們利用貝葉斯網絡對機載TTE網絡的幾種拓撲結構進行可靠性分析，并基于分析結果，總結TTE網絡的拓撲選擇和余度設計原則。

4.1 前提和假設

對TTE網絡拓撲結構的可靠性分析，假設如下：

(1)系統中的鏈路、通信板卡和交換機等部件有正常工作和故障兩種狀態，且不同部件的狀態相互獨立；

(2)系統可靠性指全端可靠性[14]，即系統中所有通信板卡之間保持連通的概率；

(3)在雙余度及多余度通信網絡中，信息流不能跨越通信板卡傳播，即在與通信板卡連接的兩條或多條鏈路中，信息不能從一條鏈路到達板卡內節點N1后，經板卡內另一節點N2，流通至與N2相連的另一條鏈路。

4.2 多種拓撲結構的可靠性分析

TTE網絡的信息交換可以采用多種拓撲結構，如環形拓撲、網狀拓撲、星型拓撲等，如圖2所示。我們以6個節點的網絡系統為例，說明各拓撲結構的可靠性。

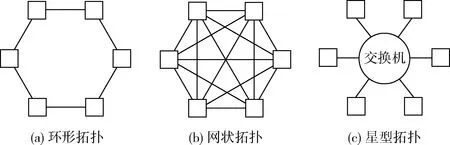
圖2 3種拓撲結構

取系統各部件的基本失效率見表2。

表2 系統各部件失效率

以環形拓撲的可靠性分析為例，說明由故障樹向貝葉斯網的轉化方法，轉化過程如圖3和圖4所示。

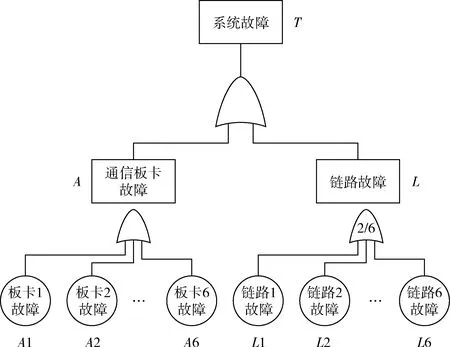
圖3 環形拓撲故障樹

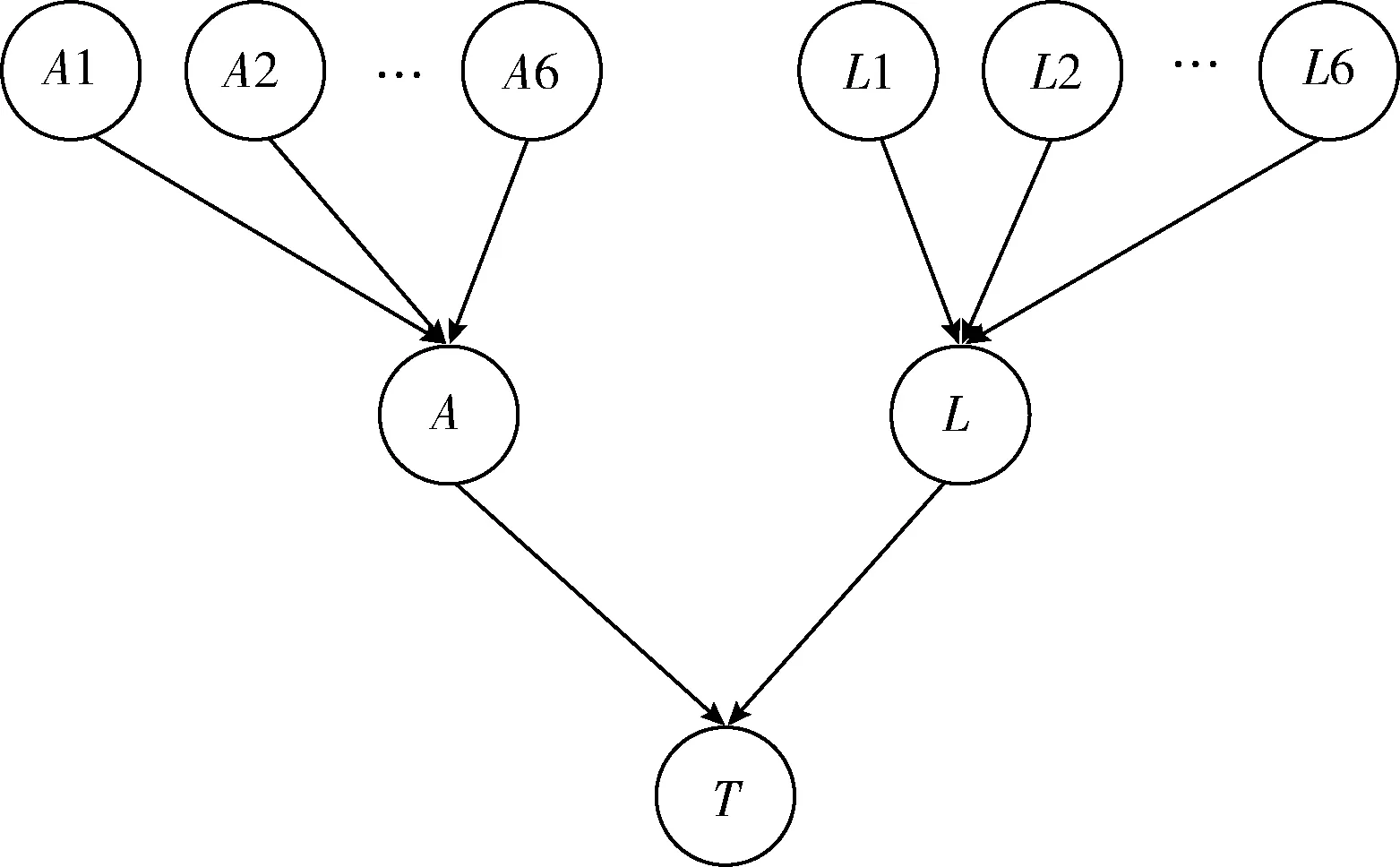
圖4 環形拓撲故障貝葉斯網

考慮系統的全端可靠性，則環形拓撲中任一通信板卡的失效或大于1條鏈路的失效都會導致系統故障，則系統故障事件T的發生依賴于所有通信板卡、鏈路的失效情況，轉化到貝葉斯網絡中，可認為T=1代表系統正常，T=0代表系統故障，A、L依此類比，則對事件T，其概率分布為

Pr(T=1|A=1,L=1)=1
Pr(T=1|esle)=0

(3)

對事件A，其概率分布為

Pr(A=1|Ai=1,i=1,2,3,…,6)=1
Pr(A=1|esle)=0

(4)

對事件L，其概率分布為

Pr(L=1|sum(Li)>4,i=1,2,3,…,6)=1
Pr(L=1|esle)=0

(5)

使用Matlab的BNT(Bayes net toolbox)，可以根據貝葉斯網絡的依賴關系，建立概率圖模型，輸入先驗概率后，得到所求事件的后驗概率。通過計算得到單余度下環形拓撲系統故障率5.9998215×10-5/h。

使用類似方法，可分別求得其它兩種拓撲結構的系統可靠性。其中，對網狀拓撲而言，其鏈路數量較多，不易得到一個狀態意義明確的故障樹，因此可以通過計算各個鏈路狀態下網絡連通性的方法，得到其貝葉斯依賴關系，這也是貝葉斯網相較于故障樹的優勢所在。最終得到單余度下，3種拓撲結構的故障率見表3。

表3 3種拓撲結構單余度故障率 ×10-5/h

航空電子系統對可靠性要求極高，表3中的故障率顯然不能滿足應用需求。因此，我們考慮通過增加冗余部件的方法提高系統可靠性。表4和表5顯示了在雙余度和三余度情況下，3種拓撲結構的故障率情況。

表4 3種拓撲結構雙余度故障率 ×10-9/h

表5 3種拓撲結構三余度故障率 ×10-13/h

為了更好地對比不同拓撲結構的可靠性，我們繪制了3種拓撲結構在不同余度情況下故障率的柱狀對比圖，如圖5所示。

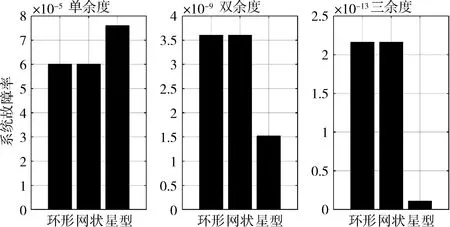
圖5 不同余度下3種拓撲結構的故障率對比

4.3 可靠性分析總結

在單余度情況下，網狀拓撲結構系統故障率最低，星型拓撲結構系統故障率最高，其原因是相對于環形拓撲和網狀拓撲，星型拓撲結構的交換機帶來的失效率增加了系統的故障率。

當系統設置為雙余度、三余度時，所有拓撲結構的故障率均會下降，而星型拓撲系統故障率下降幅度要遠大于其它兩種拓撲結構，成為可靠性最高的拓撲結構。其原因在于，對于環形拓撲和網狀拓撲而言，信息流不能跨越通信板卡傳輸，增加余度只是增加了冗余備份的系統，因此n余度系統故障率為單余度系統故障率的n次方。例如，對圖6所示的雙余度環形拓撲而言，假設所有節點都處于正常工作狀態，部分鏈路故障，從圖的連通性上看，板卡A可通過鏈路L1和L2與板卡C進行通信，但實際情況下，由于信息流不能跨板卡B流通，所以這種情況下認為系統是故障的。對星型拓撲而言，增加余度時，各個交換機之間可以互連互通，相當于增加了不同板卡間的通信路徑，因此n余度系統故障率比單余度系統故障率的n次方更小，因此在增加余度時，星型拓撲結構故障率下降得更快。

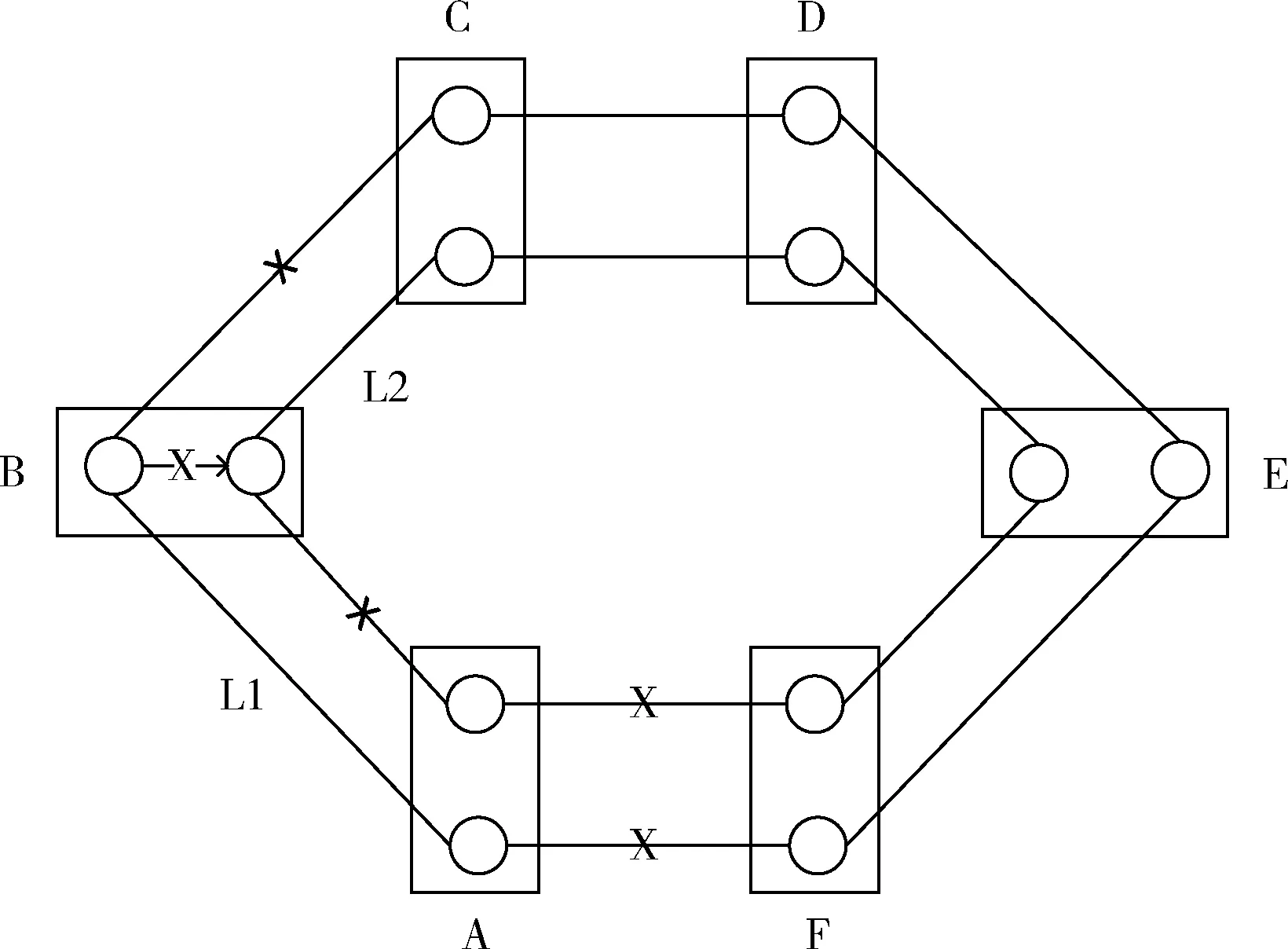
圖6 雙余度環形拓撲結構故障

相比于環形拓撲，網狀拓撲由于增加了通信板卡間的連接路徑，因此網狀拓撲的可靠性要高于環形拓撲，但經比較，其性能提高比較有限，如單余度下，網狀拓撲系統失效率為5.9998200×10-5/h，環形拓撲系統失效率為5.9998215×10-5/h。

綜上，從系統可靠性的角度分析，對于重要性較高的核心節點，可使用多余度的星型拓撲結構。對于重要性相對較低的節點，環形拓撲和網狀拓撲組網方式簡單，而網狀拓撲需增加大量的通信鏈路且可靠性提升有限，可考慮使用環形拓撲結構。

5 結束語

本文基于DIMA對通信網絡的需求，分析了TTE的特點、結構，指出TTE的高帶寬、強實時、高可靠等特性，可為未來分布式航空電子系統架構提供通信服務支撐。使用貝葉斯網絡，對TTE的幾種拓撲結構進行了可靠性分析，結果表明，星型拓撲結構在多余度時具有最高的可靠性，適合重要節點，環形拓撲結構在某些需求場景下，也有其應用價值。在機載網絡的具體應用中，需要根據不同任務場景，選擇合適的拓撲結構，可以更好滿足航空電子系統的需求。

此外，相比于傳統的故障樹分析，貝葉斯網絡具有更完備的狀態表達能力。在網絡系統可靠性分析方面，貝葉斯網絡可以通過連通性分析得到網絡系統的可靠性結果，而故障樹則很難通過割集分析或路集分析得到一個顯式的結果，體現了貝葉斯網絡在網絡可靠性分析領域的強大能力和應用前景。