AABC算法優化ELM的心臟病輔助診斷

周孟然，周悅塵，閆鵬程，胡 鋒

(安徽理工大學 電氣與信息工程學院，安徽 淮南 232001)

0 引 言

有數據顯示[1]，目前我國的心臟病患者超過六千萬人，預計未來的發病率仍將持續走高，心臟病的及早發現和診斷，對于心臟病的治療有重要意義。但是，部分心臟病檢查手段會給患者帶來創傷[2]，診斷階段嚴重依賴主治醫師的臨床經驗，具有一定的隨意性。隨著計算機技術和機器學習理論的不斷發展，計算機輔助診斷技術相比于傳統診斷方法的優勢日趨明顯，在心臟病計算機輔助診斷領域，很多學者的研究較深且成果顯著[3,4]。

極限學習機(extreme learning machine，ELM)由Huang等[5]提出，由于沒有梯度下降等迭代過程，收斂速度更快。但是，ELM的隱層輸入權值和偏置是隨機確定的，容易出現分類預測精度較低的情況。為了解決該問題，不少學者采用群智能算法對ELM的隱層輸入權值和偏置進行尋優的策略[6,7]，ELM的分類預測性能均得到了較大改善。

人工蜂群算法(ABC)是一種新型群智能算法[8]，相比于其它群算法，ABC在全局性上表現更好，但也存在局部搜索能力弱、搜索后期收斂速度慢等缺陷。針對這些缺陷，本文將最優解和次優解引入搜索機制中并且采用自適應算子μ對二者的權值進行動態調整，改進了跟隨蜂概率選擇機制，得到自適應人工蜂群算法(AABC)，構建了基于AABC算法優化ELM參數的分類模型并結合自適應遺傳算法的特征選擇應用于心臟病的輔助診斷研究。

1 基于自適應遺傳算法的特征選擇

遺傳算法(GA)作為一種群智能算法，其種群一般由二進制編碼的個體組成，可直接代表一組特征子集的選定，相比于PSO等尋優算法需要對特征設定閾值或者權值來說，更加直接和簡單。但是，由于其交叉概率Pc和變異概率Pm是預設常量，在種群進化后期優秀個體往往容易被破壞，有較高的“早熟”風險。針對這一問題，本文采用自適應進化機制[9]對Pc和Pm進行調整，使之能夠適應每一代種群不同的進化情況，改進后的Pc和Pm如下所示

(1)

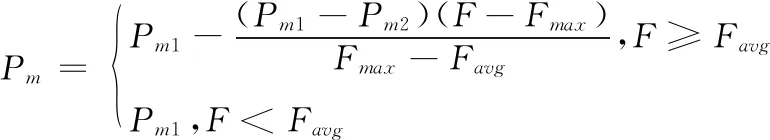
(2)

式中：Pc1和Pc2分別為最大交叉率和最小交叉率；Pm1和Pm2分別為最大變異率和最小變異率；Fmax為當前種群的最大適應度值；Favg為當前種群的平均適應度值；Fbetter為參與交叉操作的兩個個體的較大適應度值；F為參與變異操作的個體的適應度值。

利用AGA進行特征選擇的步驟如下：

(1)輸入訓練樣本的特征集合和類別標簽集合；

(2)種群初始化，個體維數等于特征數，每個個體由二進制編碼隨機產生，代表一組特征子集；

(3)計算適應度值，適應度函數采用基于類內類間距離的可分性判據，適應度公式如下

(3)

其中，Ft為當前種群第t個個體的適應度值；tr(Sb) 和tr(Sw) 分別為類間散度矩陣的跡和類內散度矩陣的跡。

(4)進行選擇、交叉、變異操作并將當前種群中適應度最大的個體帶入得到新種群，判斷是否達到終止條件，達到條件則輸出最優特征子集，否則，返回步驟(3)繼續循環。

2 基于AABC-ELM算法的分類模型

2.1 極限學習機

ELM一般由單隱層前饋神經網絡構成，也可拓展至深度網絡。ELM算法的數學描述如下：

給定樣本集

D={(xi,ti)|xi∈Rd,ti∈Rm,i=1,2,…,N}

(4)

對于含有L個隱層節點的單隱層神經網絡輸出可以表示為

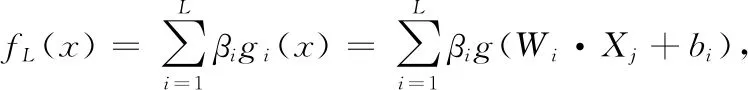
(5)

其中，g(x) 為激活函數，Xj為樣本的輸入，Wi為隱層輸入權重，βi為隱層輸出權重，bi為第i個隱層節點的偏置。

ELM的目標是使輸出誤差最小，即存在βi，Wi和bi，使得

(6)

可以矩陣表示為

Hβ=T

(7)

其中，H是隱層節點的輸出，β為隱層輸出權重，T為期望輸出

(8)

(9)

(10)

其中，H+是矩陣H的Moore-Penrose廣義逆。且可證明求得的解的范數是最小并且唯一。

2.2 人工蜂群算法

在ABC中，蜂群包含3種不同分工的蜜蜂：雇傭蜂(employed bees)，跟隨蜂(onlookers)和偵查蜂(scouts)。雇傭蜂發現食物源并記錄食物源信息。跟隨蜂根據雇傭蜂攜帶的食物源信息選擇是否跟隨。當一個食物源被放棄時，雇傭蜂轉變為偵查蜂，隨機尋找下一個食物源。

2.3 自適應人工蜂群算法

2.3.1 次優解與自適應算子μ的引入

在基本的ABC算法中，雇傭蜂和跟隨蜂的搜索依賴于隨機個體對每個個體的引導作用，導致算法的局部開發能力較弱。針對這一問題，本文對于雇傭蜂和跟隨蜂分別采用了不同的搜索機制，在雇傭蜂階段引入次優解得到新的雇傭蜂搜索公式

vi,j=xe,j+φi,j·(xe,j-xk,j)

(11)

式中：xe,j為次優解，即從種群中適應度最好的前10%個解中取一個隨機解。φi,j為(-1,1)上的隨機數。新的跟隨蜂搜索公式如下所示

vi,j=μ·xe,j+(1-μ)·xbest,j+ψi,j·(xbest,j-xk,j)

(12)

其中，ψi,j為(-1,1)上的隨機數，μ為自適應算子，能夠根據迭代次數調整最優解和次優解的權值，本文提出了一種較為簡單的線性表達式

(13)

式中：t為當前迭代次數，T為最大迭代次數，a和b為權值系數，經過多次實驗得到a和b分別取0.4和0.1為最優。

2.3.2 概率選擇機制的改進

在基本的ABC中，跟隨蜂會根據雇傭蜂提供的食物源質量選擇是否跟隨，第i個食物源被選擇的概率

(14)

其中，fit(i) 為第i個食物源的適應度值，SN為種群規模。

AABC算法的跟隨蜂選擇概率的表達式如下

(15)

其中，fitmax為當前代最大適應度值。通過對比不難發現，AABC算法的跟隨蜂對于最大適應度值的食物源是一定跟隨的，并且劃定了跟隨概率的下限，避免了在適應度值差距較小時，優秀個體不能被選擇的情況發生。

2.3.3 AABC算法的有效性測試

為驗證AABC算法的有效性，本文使用以下3個典型的無約束極小化問題進行測試，具體見表1。

表1 3個無約束極小化問題

本文選擇了標準ABC算法、全局最優人工蜂群算法(GABC)[10]與AABC算法在給定迭代次數下進行多次獨立測試。具體參數配置如下：最大迭代次數為3000代，種群規模NP取30，個體維數D為30，獨立實驗30次，個體的迭代限制limit取300。對實驗所得目標函數值的最優精度，平均精度和精度標準差進行對比分析，測試結果見表2。

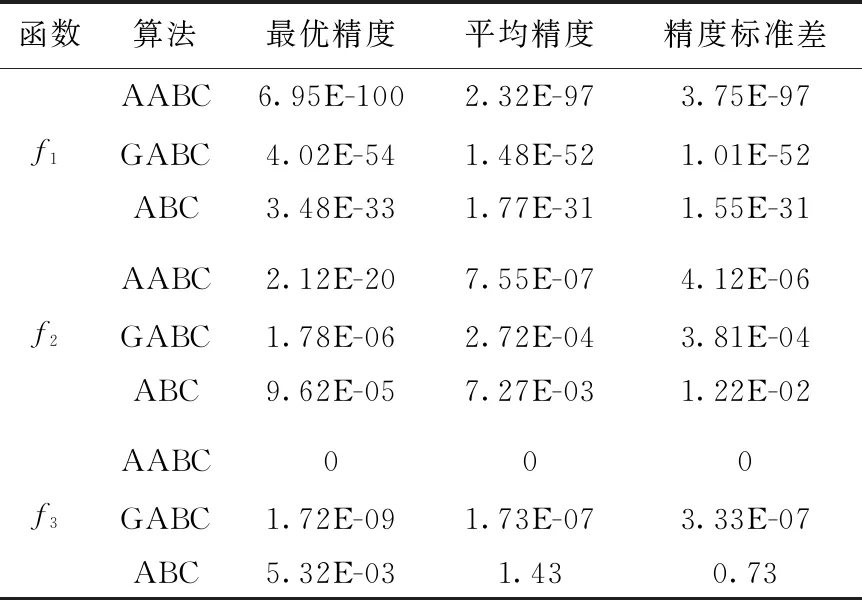
表2 目標函數測試結果

從表2可以看出，AABC算法與GABC和ABC相比，無論是在算法的收斂穩定性還是在收斂精度上，都有較大程度提升。對于Rastrigin函數，只有AABC得到了理論最優值0。對于Sphere和Rosenblock函數，雖然都未能找到理論最優值0，但AABC的收斂精度是GABC和ABC算法無法比擬的。

2.4 AABC算法優化的ELM

本文采用AABC算法對ELM的隱層輸入權值和偏置進行尋優，尋優流程如圖1所示。AABC-ELM算法的實現步驟如下所示：①初始化AABC-ELM網絡的參數，包括：最大迭代次數，種群規模，隱層節點數，個體維度，個體迭代限制等；②以ELM隱層輸入權值和偏置作為種群個體，隨機產生初始種群；③導入訓練集數據并計算目標函數值和適應度值，其中目標函數值為樣本標簽與網絡輸出標簽的均方差，ELM隱層節點的激活函數采用sigmod函數；④執行AABC算法的雇傭蜂搜索、跟隨蜂概率選擇以及跟隨蜂搜索；⑤判斷是否滿足循環終止條件。若滿足則輸出最優ELM隱層輸入權值和偏置，否則返回步驟④。

圖1 AABC算法優化ELM的基本流程

3 數據與材料

3.1 數據的獲取及預處理

仿真數據采用克利夫蘭醫學中心捐贈給UCI數據庫的Heart Disease數據集，該數據集共有303組數據，因存在數據缺失，本文只選用其中297組完整數據。此原始數據集包含了心臟病病例的76個特征，但其中存在一些明顯屬于無關特征的數據，例如患者編號、社會安全號碼、姓名等；以及一些未使用的特征，在數據集中以-9表示，包括胸痛位置、是否吸煙、吸煙年數等，共計26個無關和未使用特征，挑選剩余50組特征作為可用數據。數據標簽按照有無心臟病(>0,0)劃分為137組和160組，其中有心臟病類按照患病程度又被分為4類(1-4)，Ⅰ類54組，Ⅱ類35組，Ⅲ類35組，Ⅳ類13組。考慮到數據特征之間量綱的差別，對數據進行歸一化處理，得到的數據取值范圍為[0,1]。

3.2 選定訓練集和測試集

按照2∶1的比例將預處理后的心臟病數據隨機劃分成訓練集和測試集，采用順序劃分法，得到訓練集198組，測試集99組。

4 仿真實驗與結果分析

4.1 仿真實驗平臺

仿真實驗平臺硬件條件為英特爾奔騰G4560處理器，16 GB內存，win10專業版操作系統，在軟件Matlab R2016b環境下利用算法對數據進行仿真測試。

4.2 基于AGA的特征選擇

本文對AGA的參數配置如下：最大交叉率Pc1=0.9，最小交叉率Pc2=0.3；最大變異率Pm1=0.1，最小變異率Pm2=0.01；種群規模SN=50，最大迭代次數取1000代，最優個體適應度值隨迭代次數的變化曲線如圖2所示。

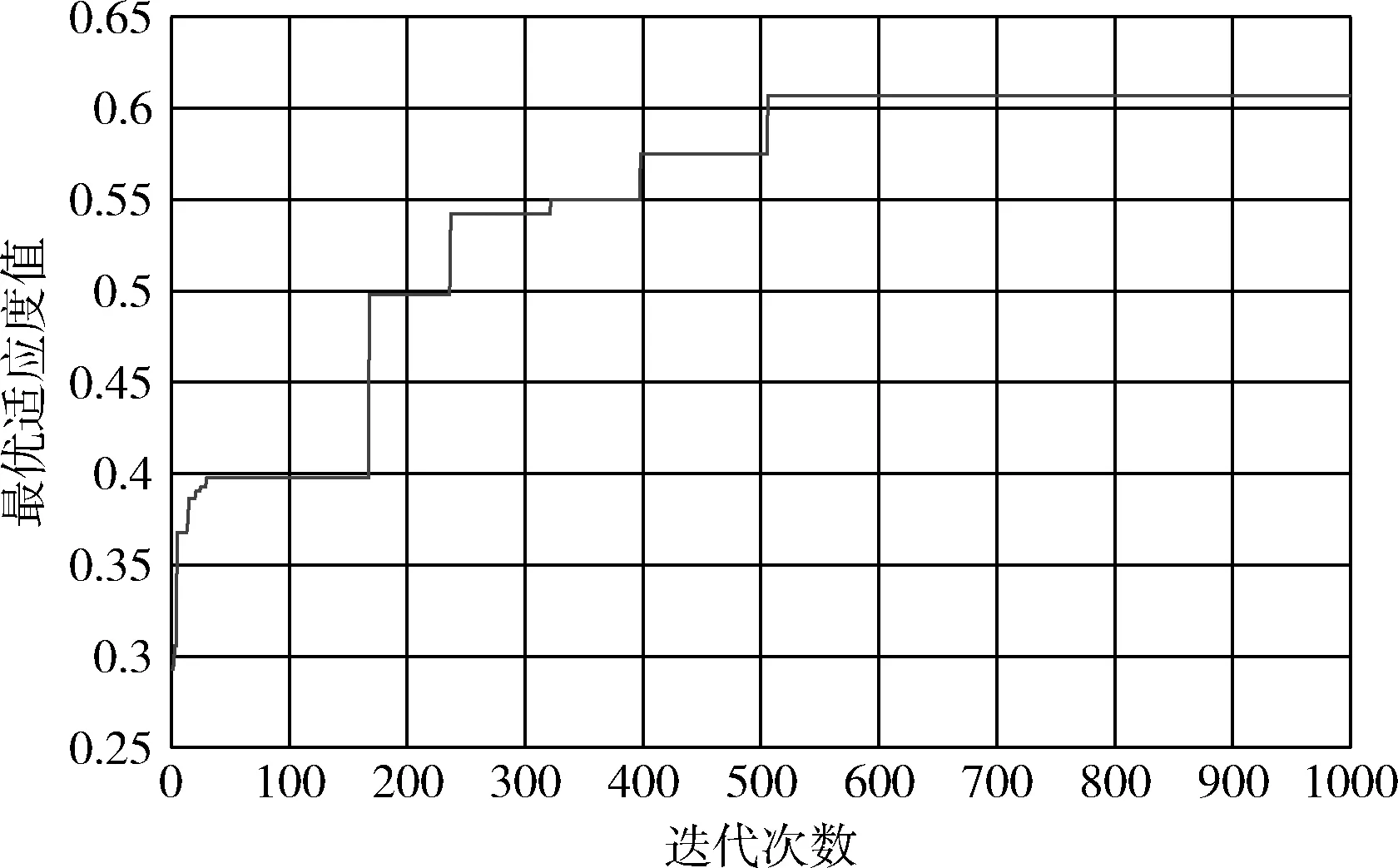
圖2 最優適應度值隨迭代次數進化曲線

從圖2可以看出AGA在算法演化初期的收斂速度較快，適應度值在50代以內就已經達到了0.4左右，之后適應度值逐步增大并在500代左右收斂，得到的最優適應度值為0.607，最優特征13個，特征序列為{6 16 18 21 27 32 34 38 40 41 42 43 45}，對應的特征依次為年齡，性別，胸痛型, 靜息血壓，血清膽固醇，空腹血糖，靜息心電圖結果，達到最大心率，運動誘發心絞痛，運動引起ST段壓降相對于休息，高峰運動ST段的斜率，通過熒光檢查著色的主要血管(0-3)的數量，地中海貧血癥。

4.3 模型參數對診斷結果的影響

針對ELM和AABC算法的特點，本文主要從以下兩個參數的選取對心臟病診斷結果的影響進行分析,按照原始數據標簽進行5分類。

4.3.1 隱層節點數對診斷結果的影響

對于存在神經網絡結構的算法來說，隱層節點的個數對網絡的輸出影響巨大，也直接影響了心臟病診斷結果。本文將AABC-ELM與PSO-ELM以及ELM算法進行比較，總體分類準確率隨隱層節點數的變化曲線如圖3所示。

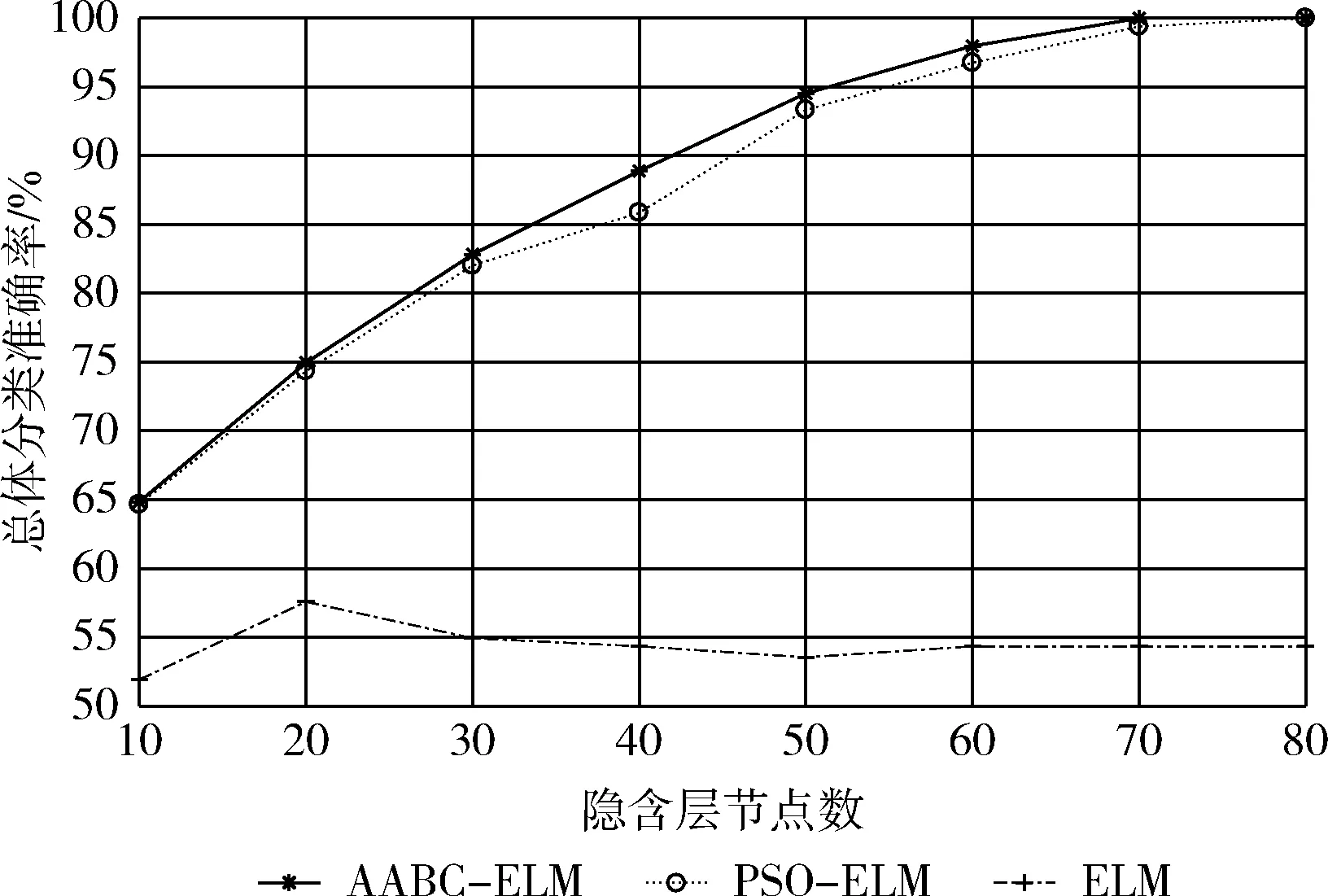
圖3 總體分類準確率隨隱層節點數變化曲線

從圖3可以看出，兩種改進后的ELM算法相比原始ELM算法在總體分類準確率上有顯著提升，表明對于ELM參數采用尋優策略進行優化是十分有效的。在相同隱層節點范圍內，相比于PSO-ELM算法，AABC-ELM算法的收斂速度更快，即在相同分類準確率的情況下所需要的隱層節點數更少，降低了網絡的復雜程度。

AABC-ELM算法在70個隱層節點時已經達到100%的分類準確率而PSO-ELM算法在80個隱層節點時才能達到，本文優先考慮分類準確率，同時盡量降低網絡的復雜程度，突出不同算法的對比效果，最后確定隱層節點數為70。

4.3.2 算法迭代次數對診斷結果的影響

因為原始的ELM算法沒有迭代尋優過程，所以本文采用AABC-ELM、PSO-ELM以及ABC-ELM這3種改進ELM算法進行仿真對比，總體分類準確率隨迭代次數的變化曲線如圖4所示。

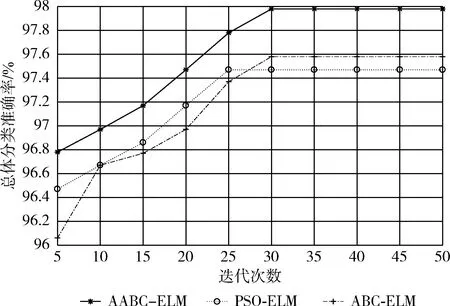
圖4 總體分類準確率隨迭代次數變化曲線

從圖4可以看出，AABC-ELM算法的收斂精度明顯高于其它兩種算法，雖然PSO-ELM算法要更早收斂。ABC-ELM算法的收斂曲線波動要更大一些，但收斂精度卻略高于PSO-ELM算法，可見ABC-ELM算法全局性能更優。

4.4 心臟病診斷的仿真結果分析

為了測試AABC-ELM算法對Heart Disease數據的分類識別效果，本文采用AABC-ELM、IAFSA-ELM、ABC-ELM、PSO-ELM、ELM以及BP神經網絡對心臟病診斷的198個訓練樣本和99個測試樣本分別進行學習和分類。按照原始數據標簽(0-4)進行5分類以及按照有無心臟病(0,大于等于1的值為1)進行2分類。測試集各標簽樣本個數見表3。

表3 測試集各標簽的樣本數

對于心臟病診斷的仿真參數配置如下：最大迭代次數為100，個體迭代次數限制為20，種群規模NP取50，獨立實驗20次。各算法對于五分類和二分類平均心臟病分類結果見表4、表5。

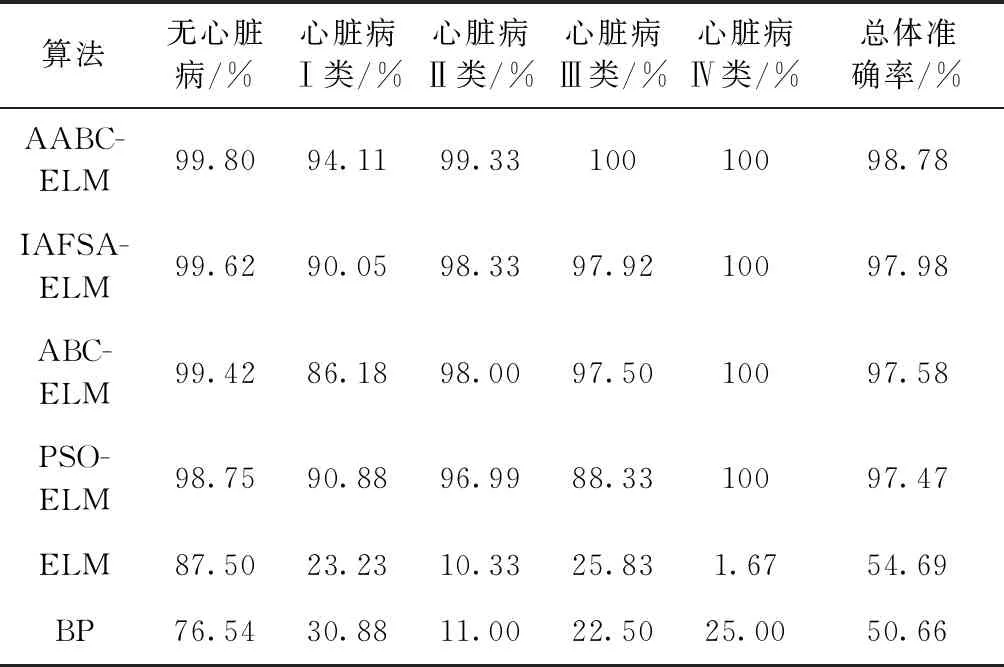
表4 幾種算法的五分類平均心臟病分類結果

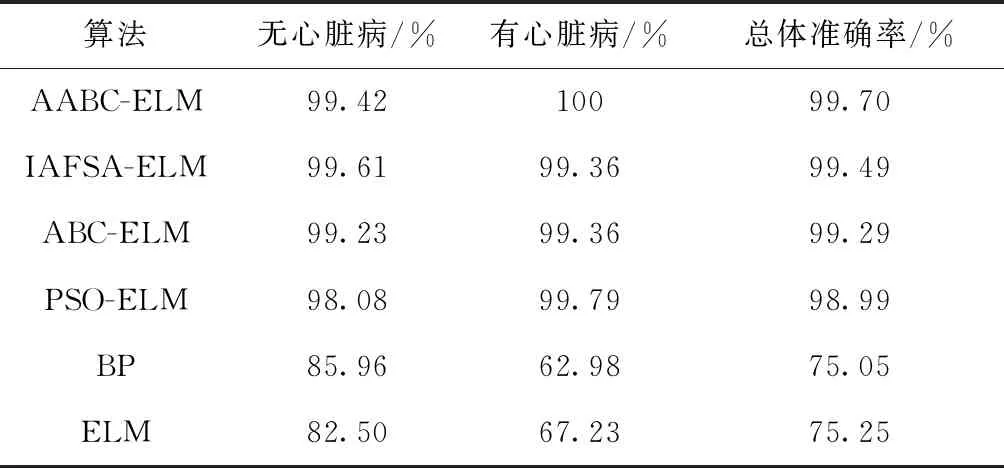
表5 幾種算法的二分類平均心臟病分類結果

結合表3～表5不難看出，無論是五分類還是二分類，幾種改進ELM算法的分類結果要明顯好于ELM和BP。值得注意的是，在樣本分布不均勻的五分類中，ELM和BP對于小樣本數據分類的表現很差，ELM算法對于樣本數最少的心臟病Ⅳ類幾乎無法識別。然而對于樣本數量相近的二分類(無心臟病52組，有心臟病47組)，總體分類準確率相比于五分類要高出20%左右。在五分類中，AABC-ELM對于各標簽的分類準確率均為最高，其中心臟病Ⅲ類和Ⅳ類的分類準確率達到了100%；在二分類中，AABC-ELM對于無心臟病類的分類準確率要略小于IAFSA-ELM，對于有心臟病類的分類準確率達到了100%，相比于ELM算法，五分類和二分類的總體分類準確率分別高出44.09%和24.45%。

對于心臟病診斷耗時的研究，由于不同算法達到不同的分類準確率的耗時各不相同，所以本文以97%的五分類準確率為標準，而ELM和BP無法達到這個標準，所以只采用AABC-ELM、IAFSA-ELM、ABC-ELM以及PSO-ELM進行對比，4種算法的平均耗時見表6。

從表6可知，AABC-ELM相比于IAFSA-ELM、ABC-ELM以及PSO-ELM算法，網絡的訓練以及測試耗時大大縮短，表明在保證一定的分類準確率下，AABC-ELM算法的學習速度更快，能更好滿足心臟病診斷的時間要求。

4.5 算法泛化性能測試

泛化性能，即對新鮮數據的適應能力是衡量一種算法是否可靠的關鍵因素之一，如果說本文算法對于不同的心臟病數據都能取得良好的分類效果，則可以說本算法具有較強的泛化性能。為對本文算法的泛化性能進行測試，現采用UCI數據庫中的SPECT心臟病數據集進行仿真實驗，單光子發射計算機斷層成像術(single-photon emission computed tomography，SPECT)是一種核醫學CT技術，可以對心臟灌注斷層進行顯像。該數據集共有267組樣本，樣本特征為心臟SPECT-CT圖像的感興趣區域，共有44組特征，樣本標簽分為正常(0)和異常(1)；原始數據集已將樣本劃分為187組測試集(正常15組，異常172組)和80組訓練集(正常40組，異常40組)，首先采用AGA對數據特征進行選擇，得到12個最優特征，再進行AABC-ELM建模，與ELM的仿真結果對比見表7。雖然本文算法對正常樣本的分類準確率僅為73.33%，但較ELM仍提高了40%，對于異常樣本則全部分類正確，總體分類準確率提高了34.12%。

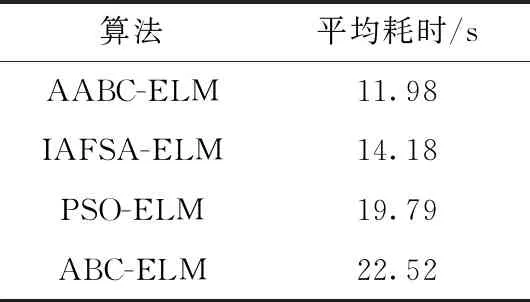
表6 4種算法對心臟病診斷的平均耗時

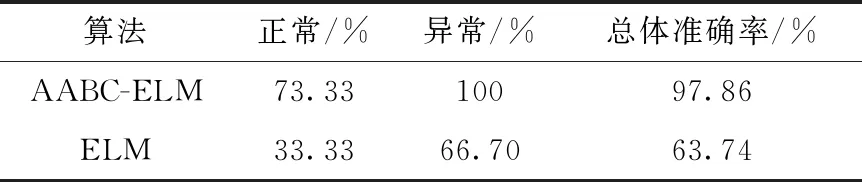
表7 兩種算法在SPECT數據集上的分類結果

5 結束語

本文利用AGA對心臟病數據集進行特征選擇，結合AABC算法優化的ELM建立了心臟病輔助診斷模型。仿真結果表明：①本文算法有效的彌補了ELM對于不均衡心臟病樣本識別精度不足的缺陷，具有較高的分類準確率、較短的訓練時間，降低了算法欠擬合風險；②本文算法對新鮮數據具有較好的適應能力，泛化性能較強，不僅適用于心臟病患病程度的識別，還適用于心肌缺血的識別。

在本文基礎上，可以考慮將ELM與深度學習相結合，對心臟病圖像的識別分類進行深入研究。