基于優化計算的駕駛員模型及其在功能安全設計中的應用

徐志峰 張兆龍 周炳峰

（北京新能源汽車股份有限公司，北京 100176）

主題詞：電動汽車 功能安全 車輛動力學仿真 駕駛員模型

1 前言

在功能安全等級評定時，需要模擬電控功能失效可能帶來的事故，以及事故的可控性、嚴重度及故障容忍時間[1]。通過搭建“駕駛員-車輛-環境”系統的虛擬模型[2]進行不同危險工況下的仿真，以獲取電控功能失效的影響數據是常用方法之一。

建立能夠模擬具有不同駕駛經驗的駕駛員模型，是功能安全仿真的關鍵，當前，相關研究尚處于起步階段。車輛側向位移和車輛橫擺角狀態是駕駛員操縱轉向盤時所依據的主要參數[3-4]，對于欠缺駕駛經驗的駕駛員，因為將車輛等效為一個質點，從而需要更多考慮車輛位移與預期是否相符的問題；而對于經驗豐富的駕駛員，則需要更多考慮車輛橫擺姿態的平滑調節以確保車輛行駛軌跡滿足要求，同時保證車輛行駛時具有較高的穩定裕量。

此外，當考慮車輛橫向位移與目標軌跡誤差進行轉向盤轉角決策時，準確地計算誤差值將直接決定車輛的循跡精度。現有文獻提出的駕駛員模型在計算車輛橫向位移誤差時大多基于預瞄時間內車輛的縱向位移，再由縱向位移與橫向位移的對應關系識別出預瞄點位置[5]。車輛轉向行駛過程中，轉向角實時變化，上一時刻確定的預瞄點并不能到達，而且現有算法在進行轉向盤轉角決策時，也缺乏轉向角對車輛行駛穩定性影響的考慮。

本文將在準確描述車輛側向位移誤差的基礎上，提出一種兼顧車輛循跡能力與行駛穩定性的雙目標優化控制策略，并在模型中設置可根據駕駛員駕駛表現調節的參數，從而模擬不同駕駛水平的駕駛員在發生電控功能失效時的表現，最終評定電控功能失效的影響及其功能安全等級。

2 基于多目標優化的駕駛員模型

為建立計算量小、有一定循跡能力，且能夠防止由于轉角施加不當影響車輛側向附著裕度的模型，本文轉向盤轉角決策算法采用單點預瞄駕駛員模型，且在轉角計算時考慮車輛側向附著水平。在提出的駕駛員模型中，同時考慮車輛側向位移誤差以及車輛前、后軸側偏水平進行轉向盤轉角的優化計算。具體步驟為：根據事先規劃的行駛路線進行預瞄區間內目標軌跡辨識，以尋求最小化預瞄區間內車輛側向位移誤差與車速方向誤差，同時優化車輛轉向特性為目標，進行轉向盤轉角決策。

2.1 轉向盤轉角決策算法

2.1.1 目標軌跡的確定

在車輛坐標系內，將目標軌跡橫向坐標擬合為縱坐標的函數：

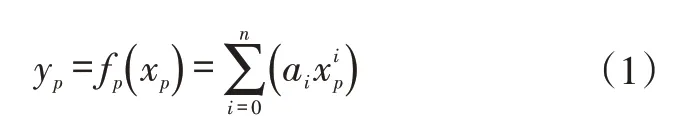
式中，yp和xp分別為車輛坐標系下目標軌跡上預瞄點p處的橫坐標與縱坐標；ai為所擬合函數中的系數。

車輛在轉向工況下行駛時，式（1）中n≥2，即目標軌跡為非線性函數。本文將目標軌跡擬合為二次函數[6]：

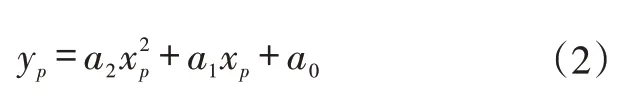
2.1.2 橫向位移誤差的確定

為確定時間T后車輛在當前坐標系xoy下的位移，引入簡化的單軌車輛模型[7]，如圖1 所示。圖1 中，oxyz為車輛坐標系；Oc為車輛的轉向中心；δ為前輪轉角；v1、v2分別為前、后輪輪心速度；α1、α2分別為前、后輪輪胎側偏角；Fy1、Fy2分別為前、后輪受到的地面側向附著力；l為軸距；a、b分別為質心到前、后軸的距離；V為車輛質心速度；u、v分別為車輛質心沿縱向、側向的速度；γ為車輛橫擺角速度。

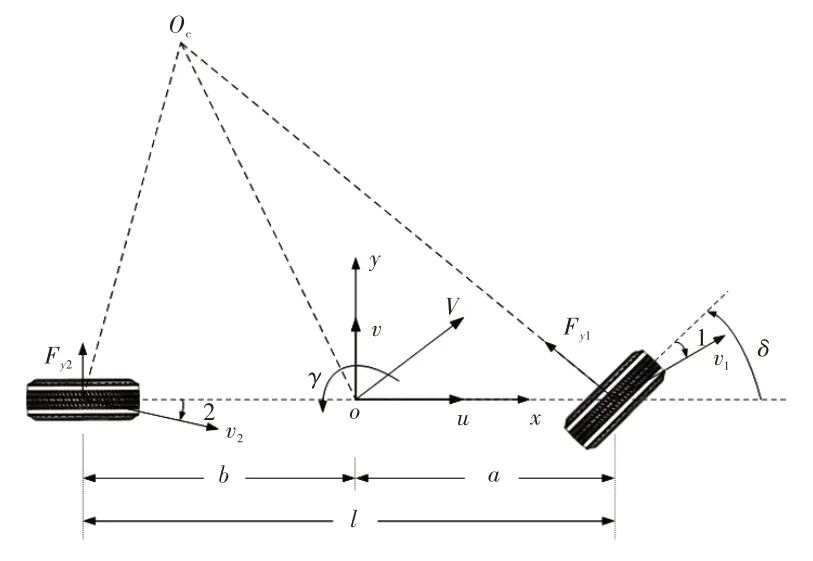
圖1 單軌車輛模型

根據上述簡化模型，車輛位移(xt,yt)為：

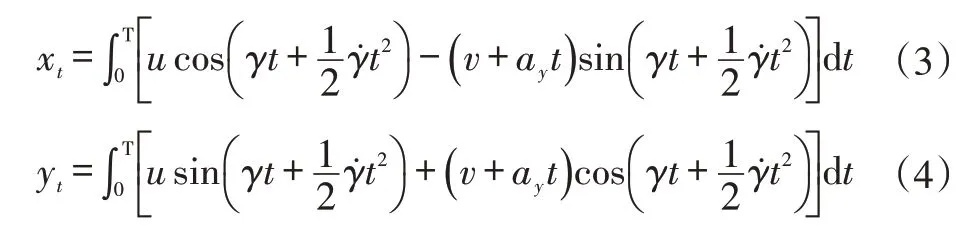
可近似求得：

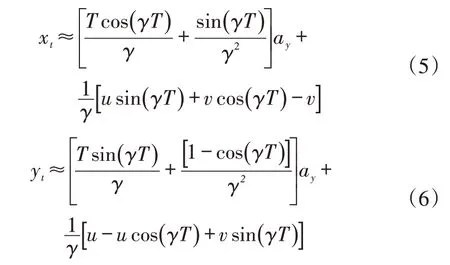
進一步可得側向位移差為：

式中，ypt為預瞄時間為T時，預瞄點在目標軌跡上的橫向坐標。

考慮到ay∝δ，可得：

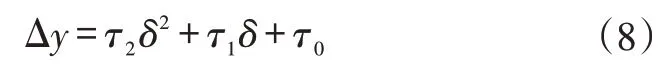
式中，τ0～τ2為各次項的系數，可由式（2）～式（7）計算得出。

2.1.3 車輛轉向特性約束

本文提出的車輪轉角控制策略考慮了車輛前、后軸側偏角的均衡。根據單軌車輛模型的運動學關系推導可得[8]：

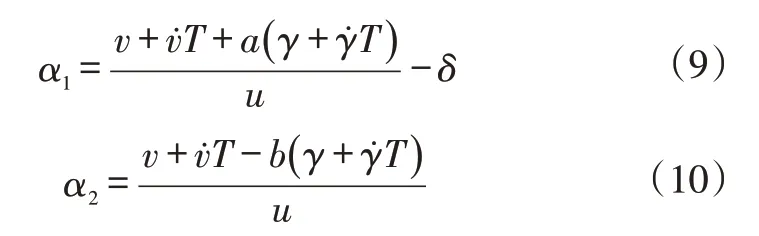
引入側偏角之差Δα：

式中，σ1和σ0為整合后的系數。

2.1.4 轉向盤轉角優化控制

假設駕駛員通過Δy和Δα的最小化進行轉向盤轉角δopt決策，抽象為求解以下優化問題[9]：

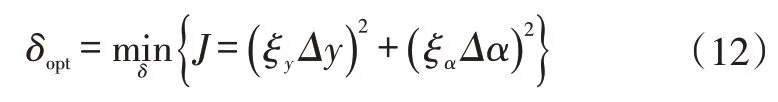
式（12）中的目標函數J可表示為：

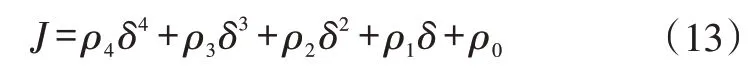
式中，ξy、ξα分別為Δy和Δα的權重系數；ρ0～ρ4為整合后的系數。

2.2 問題求解

本文采用一種兼顧計算成本與結果精確性的簡化求解方法。假設預瞄時間內車速不變，基于此方法得到預瞄點的確切位置，此時得到簡化的目標函數，并由高次函數轉變為二次函數，求解可得到初步最優點δd。

假設預瞄時間T內車輛處于車速不變的穩態轉向行駛狀態，此時計算出預瞄時間T后車輛的位置為(xt0,yt0)。車輪轉角由δ調整為δt，可得到車輛側向位移誤差為：

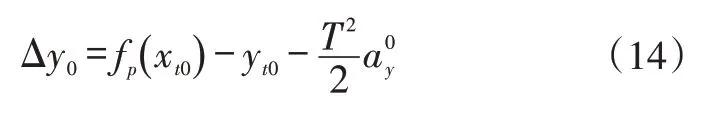
此時Δy0∝δt，多目標優化問題轉化為二次凸優化：

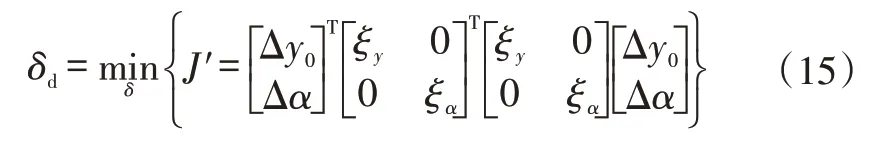
轉化為二次凸優化后，求解方法不再贅述[10]。

2.3 考慮駕駛員反應滯后的轉角

決策出最優轉向盤轉角后，駕駛員操縱轉向盤進行目標轉角跟蹤。考慮到人體的神經系統反應滯后和慣性反應滯后，增加滯后處理環節[11-12]。最終可以得到轉向盤轉動的角度δo與理論最優轉向盤轉角δd的關系為：

式中，(1+ths)為駕駛員操縱汽車轉向盤的慣性反應滯后；th為慣性反應滯后時間；為駕駛員神經系統的反應滯后；td為神經反應滯后時間。

在低頻域內可得：

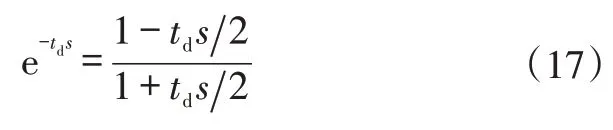
3 仿真模型及驗證

3.1 仿真模型

本文搭建的仿真模型由駕駛員模塊、電驅動系統模塊、制動系統模塊、車輪與車體運動模塊、變路面坡度及附著系數路面組成，搭建車輛具備橫向車速、縱向車速、橫擺角速度、4 個車輪旋轉角速度和轉向車輪轉角共8個自由度[13]，布局如圖2所示。

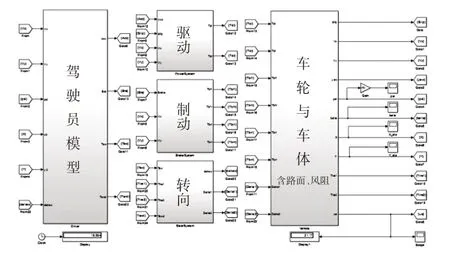
圖2 “駕駛員-車輛-環境”仿真模型

仿真模型中，變附著系數路面用于仿真鄉村公路局部路面有積雪或結冰等情況。本文模型的輪胎與路面接觸力矩中，根據當前車輪的位置在線調整輪胎模型中的路面附著系數，以體現路面局部結冰對附著力的影響[14]，變附著系數路面模塊包含在車輪與車體模塊中，如圖3所示。

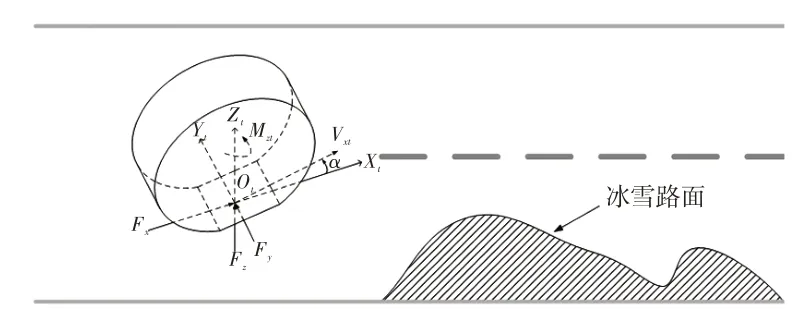
圖3 變附著系數路面模型示意

3.2 仿真模型標定及驗證

為確保模型準確，應用某車型開展實車測試，根據所采集數據進行模型的標定與驗證。車輛參數如表1所示。

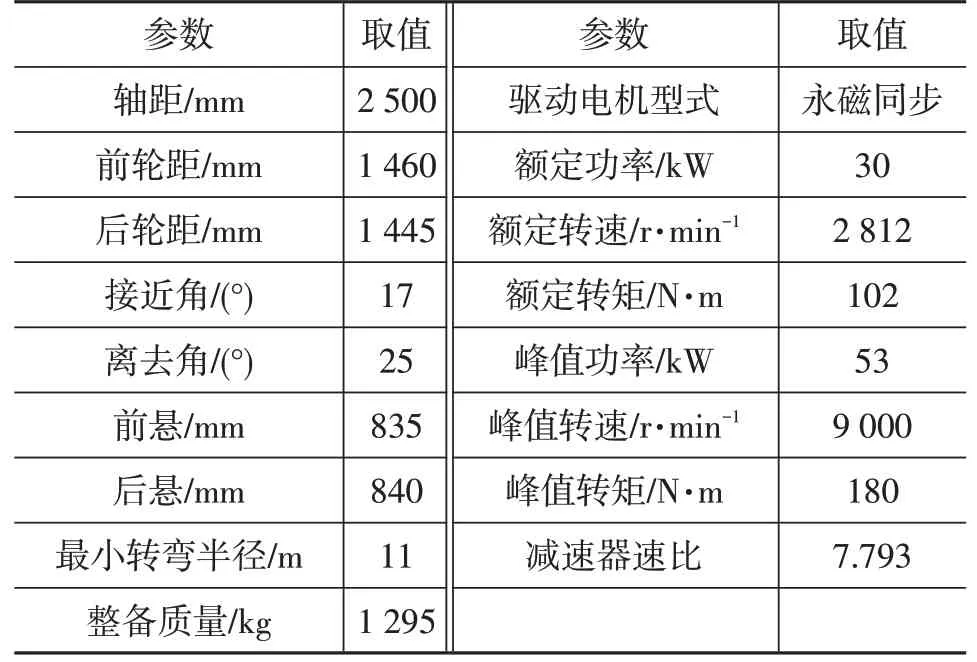
表1 試驗車參數

為完成模型的標定與驗證，應用試驗樣車分別開展了2 種工況的數據采集：一是直行加速后滑行制動試驗，目的是驗證從油門踏板輸入到車速的響應特性；二是雙移線試驗，目的是驗證從轉向盤轉角輸入到車輛轉向行駛的響應特性。

在進行直行試驗時，車輛在起步狀態下，駕駛員松開制動踏板后迅速踩下油門踏板使車輛加速行駛至100 km/h，此后松開踏板，僅通過操縱轉向盤維持車輛直線行駛，至車速減小至6 km/h 左右時停止試驗，試驗過程中記錄電機的輸出驅動扭矩、回饋制動扭矩及轉速數據。以采集到的油門踏板開度、驅動扭矩數據作為輸入，導入模型。驗證數據及結果如圖4、圖5所示。

在進行雙移線試驗時，車道及布樁情況如圖6 所示[15]。圖6 中，S1=15 m，S2=30 m，S3=S4=25 m，S5=30 m，B1=1.1B+0.25 m，B2=1.2B+0.25 m，B3=1.3B+0.25 m，其中B為車輛寬度。測試結果及仿真結果如圖7所示。

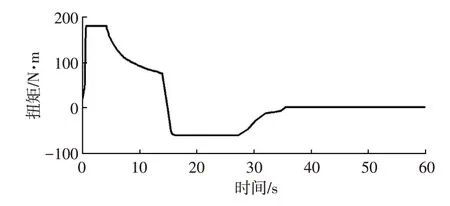
圖4 直行試驗驅動、回饋制動扭矩

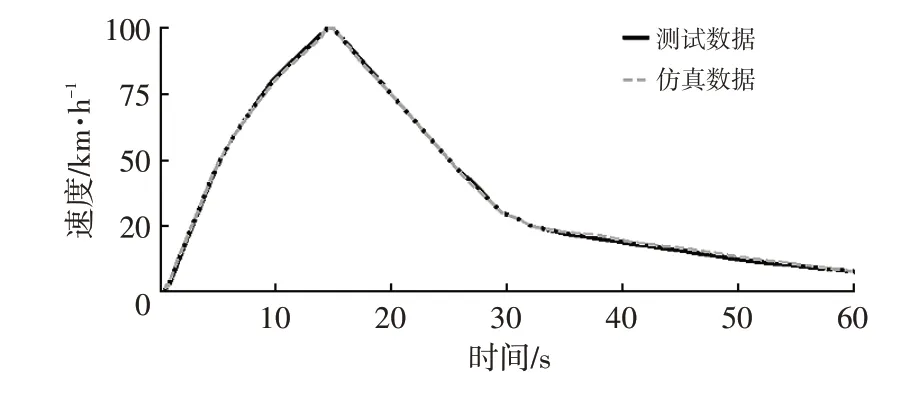
圖5 車速響應對比

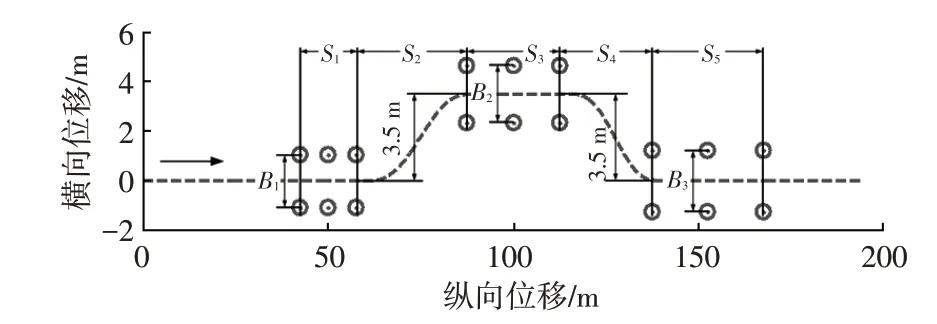
圖6 標準規定的雙移線路徑及布樁位置示意

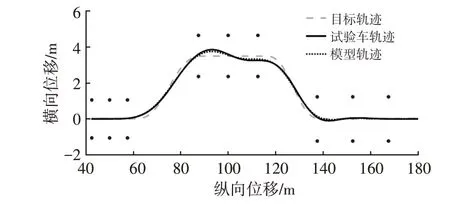
圖7 雙移線工況下車輛軌跡對比

4 基于駕駛員模型的功能安全等級仿真

4.1 駕駛員模型標定

邀請30 位駕駛員應用試驗車進行雙移線駕駛試驗，根據每個駕駛員的駕駛軌跡，標定出不同的駕駛員模型參數組{ξy,ξα,T,th,td}n，其中n=1,…,30。根據30位不同性別、不同駕齡駕駛員的軌跡數據，最終擬合出1位代表30位駕駛員平均水平的“虛擬駕駛員”。30位實際駕駛員及1 位虛擬駕駛員駕駛車輛在雙移線工況行駛的軌跡如圖8所示。

4.2 功能安全仿真

在制動能量回收控制功能的功能安全設計過程中[16]，為確定“非預期峰值制動能量回收力矩”失效模式下造成危害事件的嚴重度、可控性及故障容錯時間，進行仿真計算。

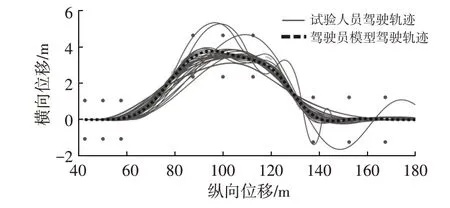
圖8 實際和虛擬駕駛員雙移線工況行駛軌跡

車輛A以30 km/h的初始車速行駛在城市道路的濕滑路面時，駕駛員進行雙移線避障（車輛B為障礙車）駕駛[17]，此時出現最大制動能量回收力矩，導致車輛前軸發生抱死，轉向失控，有可能引發碰撞，如圖9所示。

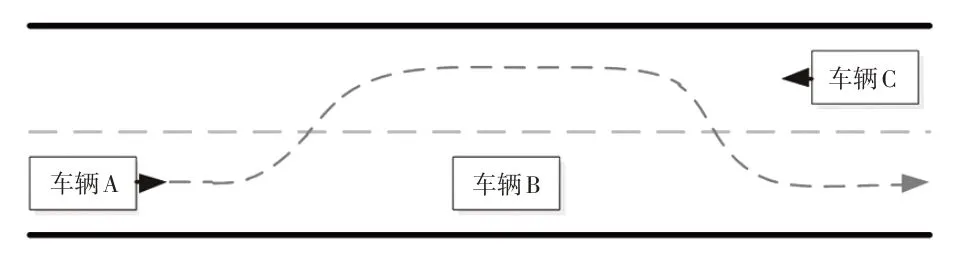
圖9 仿真場景示意

仿真結果如圖10所示。當峰值能量回收力矩施加在車輛前軸后，駕駛員失去對車輛的控制，可控性為C3。圖11 所示為圖10 中反向橫擺的局部放大。由圖11可知，雖然駕駛員逆時針轉動轉向盤，但由于前輪回饋制動施加扭矩，使車輛受到與轉向盤旋轉方向相反的橫擺力矩，最終出現了反向橫擺的情況。

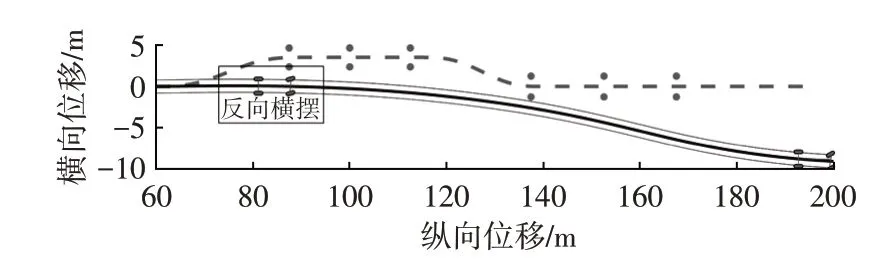
圖10 故障狀態下雙移線行駛車輛的行駛軌跡

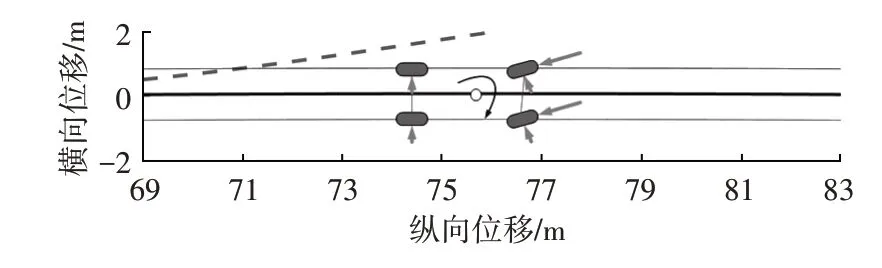
圖11 反向橫擺受力分析

由于車輛側向失穩，沒有及時完成變道行駛，車輛與當前車道的障礙物發生碰撞。碰撞車速為24.9 km/h，嚴重度為S2。結合濕滑路面暴露率E3，可評定制動能量回收控制功能的功能安全等級為ASIL B。據此制定安全目標為“避免行駛中出現峰值回饋制動力矩，造成車輪抱死側滑”，與此對應的安全狀態為“驅動電機輸出的回饋制動扭矩為零”。

隨后計算故障容忍時間[18]，仿真結果如圖12 所示。由仿真結果可知，當非預期峰值扭矩最大施加時間為300 ms 時，駕駛員能夠駕駛車輛完成雙移線行駛，據此確定故障容忍時間為300 ms。

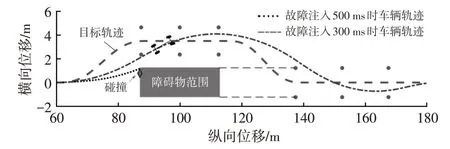
圖12 故障容忍時間內峰值回饋扭矩消除后車輛行駛軌跡

5 結束語

本文設計了基于多目標優化的駕駛員模型，并將其應用于功能安全設計仿真環節，研究結果表明：

a.基于最小化橫向位移差及車輛前、后軸側偏角差進行下一時刻轉向盤轉角計算，并根據不同駕駛員設置多目標優化中目標函數權重參數，能夠模擬不同駕駛技能水平駕駛員；

b.建立“駕駛員-車輛-環境”系統模型，進行不同“駕駛員”駕駛下電控功能發生失效時的仿真，有助于消除車輛出現事故的風險，適用于電控功能的功能安全等級評定；

c.進行仿真分析后，明確某車型的制動能量回收控制功能在回收力矩失控這一失效模式下，設計應遵循的安全目標為“避免行駛中發出峰值回饋制動力矩，造成車輪抱死側滑，功能安全等級為ASIL B級，故障容忍時間為300 ms”。