轉向節主銷與轉向輪間轉向運動及轉角誤差分析＊

王成志 王云超

（集美大學，廈門 361021）

主題詞：轉向梯形 定位角參數 運動分析 轉角誤差 轉角計算誤差

1 前言

轉向機構運動設計與車輪實際轉角和理想轉角的計算有關，這兩者的計算誤差必然影響車輛轉向機構的設計。車輪實際轉角涉及左、右主銷之間和主銷與車輪之間2類運動傳遞。前者的相關研究文獻較多，計算模型有近似的平面模型[1-3]和精確的空間模型[4-5]；后者與車輛轉向輪的主銷內傾角、主銷后傾角、車輪外傾角與前束角這4 個定位角參數有關，嚴格來說，目前還缺乏其運動的精確計算模型。對斷開式車橋的轉向梯形進行運動分析時，一般直接用轉向輪車輪軸在水平面內的轉角變化作為車輪轉角[6-7]。而整體式車橋的轉向梯形運動分析則分為多種情況：許多文獻[1-5]并不考慮主銷與車輪之間的運動差異；文獻[8]、文獻[9]等將主銷轉角按水平角速度分量分解獲得車輪轉角，但只考慮主銷內傾與主銷后傾的影響；文獻[10]等提出的球面三角學計算模型由于考慮了外傾角對轉動的影響，計算精度明顯提高，但依然忽略了車輪前束角對轉向的影響。另外，用球面三角學建立的模型沒有解析的反解，也未考慮初始前束角影響。如果使用存在誤差的計算模型進行優化設計，會影響設計精度或影響對車輛運動性能的判斷[11]。

理想轉角采用阿克曼理想轉向條件計算時，主銷中心距或輪距K和車輛軸距L有多種不同定義，有些定義會給理想轉角自身帶來計算誤差[12-13]。

本文重點建立考慮4個定位角參數的車輪轉角計算數學模型，以此為基礎，分析用各種模型計算轉角時轉向機構中各部分計算誤差，并分析誤差對機構總轉角誤差的影響，根據獲得的接地點坐標定義合理的K、L取值。

2 主銷及車輪運動模型

2.1 幾何分析原理

車輛轉向輪的主銷內傾角α0、主銷后傾角β0、車輪外傾角λ0與前束角τ0等的定義如圖1所示。圖1中，DC為主銷軸線，D點為主銷軸線與車輪旋轉軸線的交點，點M0為車輪輪心，D與M0的距離為m（DM0連線為車輛直行時的車輪軸線初始位置）。主銷轉動360°時，輪心M0則繞主銷轉動1周，形成的軌跡是圓心在主銷軸線上以O為圓心，半徑為mr的空間圓ζ；而車輪軸線形成一個以DM0為母線，底圓為ζ，半頂角為φ的虛擬正圓錐體。

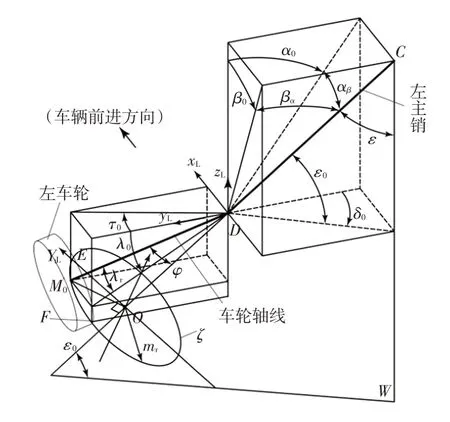
圖1 定位參數及車輪輪心軌跡

在圖1的D點建立如圖所示的DxLyLzL坐標系，將空間圓ζ沿zL負方向拉伸或投影到水平地面H上，得到圖2所示的橢圓柱體。以ζ的圓心O為原點建立坐標系OXLYLZL，ZL軸與左主銷重合，YL軸為圓錐底圓ζ所在斜面與W面（通過主銷的豎直垂面，即YLZL平面）的交線OE（E點為底圓ζ的最高點），斜向上為正。YL軸線和車輪軸線DM0在水平面H上的投影分別為若左主銷轉動角度為θL，即在圓錐底圓ζ上從OM0轉過角度θL到達OM（設車輛右轉），則左車輪軸線位置DM0轉到新位置DM，而在水平投影面上，左車輪軸線的投影從初始位置D′M0′轉過角度δL到達D′M′、OM0的投影從轉到O′M′。δL即為車輪繞垂直軸zL轉過的角度，相當于θL的水平分量。這時OM與YL軸的夾角為θ，D′M′與D′O′的夾角為δ（δ相當于θ的水平分量，以點D在水平面的投影點D′為角的頂點），兩者的對應關系可通過θ的投影角σ來關聯。YL軸正向、D′O′（D′指向O′為正）是角度θ、δ的測量起始標示線，都位于通過左主銷的豎直垂面W上。分別為θL、δL的測量起始標示線。

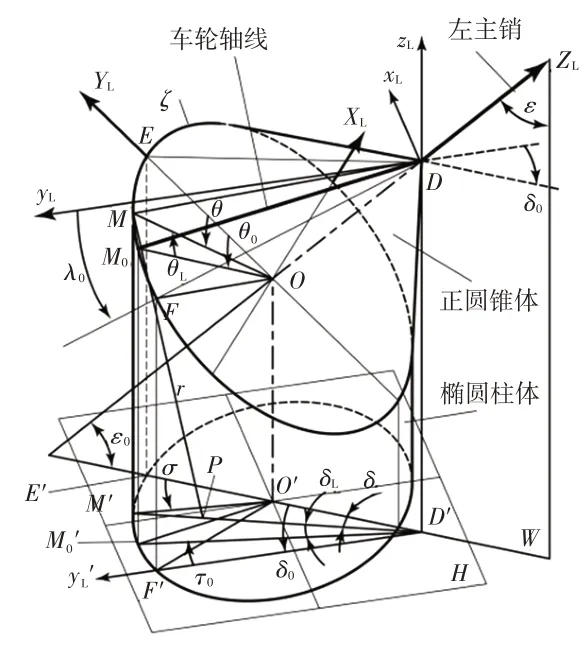
圖2 左主銷轉角與左轉向車輪轉角投影關系

圖3所示為右主銷的幾何投影關系。同理，假設右主銷轉動角度為θR，即在圓錐底圓上ORN0轉過角度θR到達ORN（設車輛右轉），則右車輪軸線從AN0轉到AN，而在水平投影面上，右車輪軸線的投影從A′N0′轉過δR到達A′N′，ORN0的投影從轉到。這時ORN與YR軸、A′N′與的夾角分別為θ′、δ′，它們的測量起始標示線YR軸都位于通過右主銷的豎直垂面W′上。

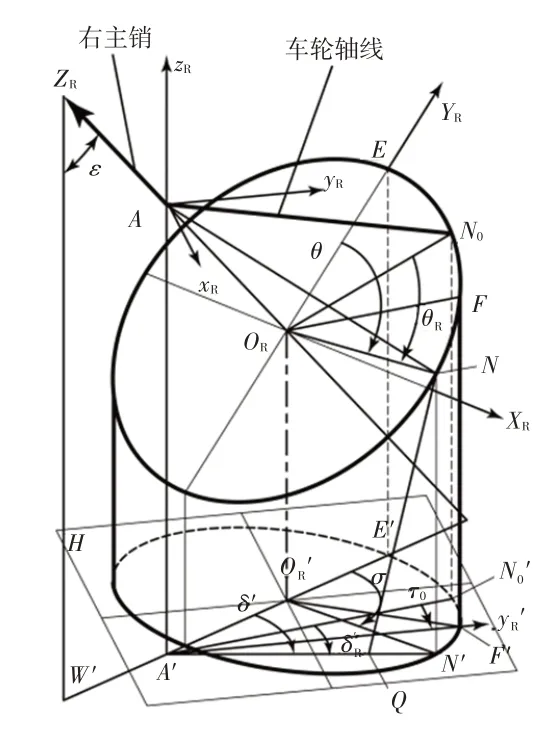
圖3 右主銷轉角與右轉向車輪轉角的投影關系

顯然，先要確定θ（θ′）與δ（δ′）的關系。

2.2 斜面角度投影及主銷轉角水平分量

在圖1的DxLyLzL坐標系中，DO與DM0上的單位向量分別為：

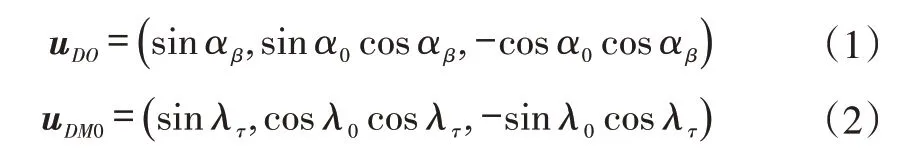
式中，αβ=arctan(cosα0tanβ0)為主銷軸線與其在yLzL平面上的投影間的夾角；λτ=arctan(cosλ0tanτ0)為車輪軸線與其在yLzL平面上的投影間的夾角。

依據式（1）和式（2），根據空間向量的夾角公式，圓錐的半頂角為：

式 中，χ=sinαβsinλτ+sinα0cosαβcosλ0cosλτ+cosα0cosαβsinλ0cosλτ為由4 個定位參數決定的半頂角的余弦。

從圖2 中切出如圖4a 所示的計算模型。為便于觀察分析，將圖2 中的圓錐體和橢圓柱體投影到W平面、XLYL平面和水平面H上，結果如圖4b～圖4d所示。

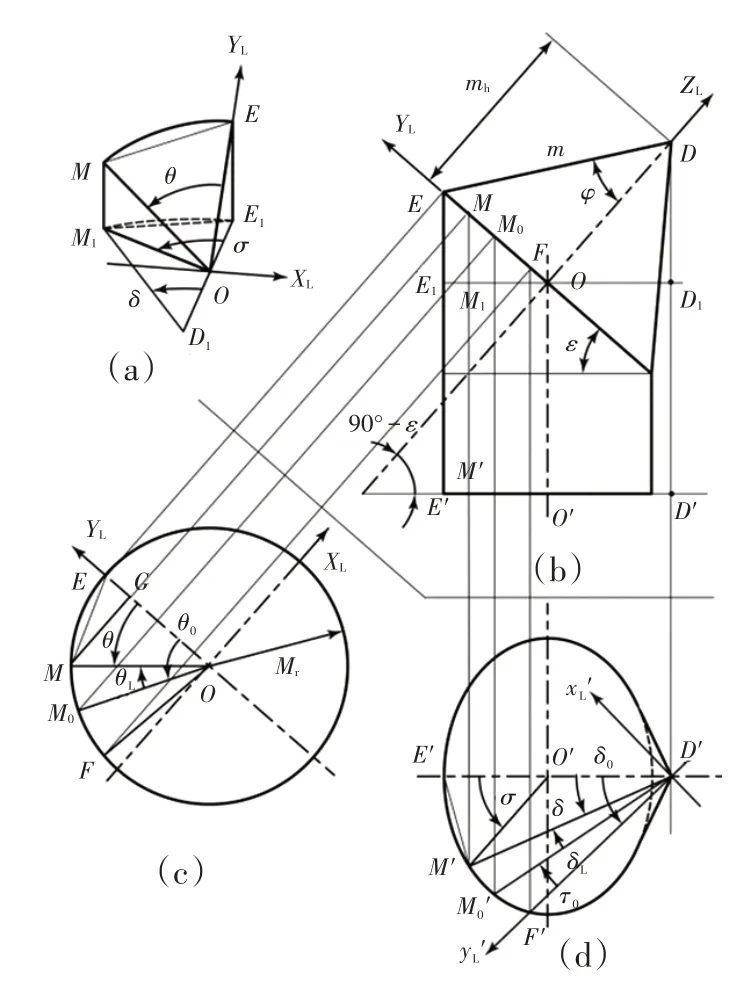
圖4 左主銷轉角與左轉向輪轉角的幾何關系

借助圖4b可以求出圖4a中的四邊形EE1M1M（其中EE1和M1M都與E1M1垂直）中EE1、MM1的長度和。再由圖4c求出----EM后，有：

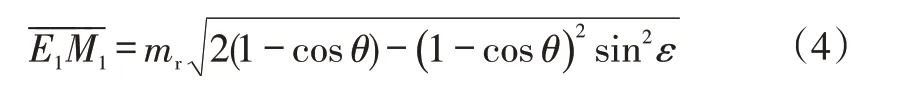
式中，ε=arccos(cosα0cosαβ)為主銷軸線與鉛垂線的夾角。

在△OE1M1（即△O′E′M′）中，可以求出邊長和，所以又有：

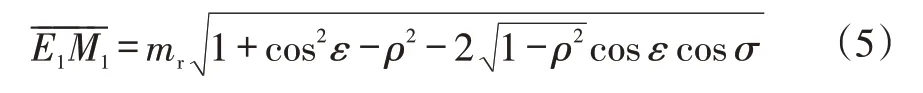
式中，ρ=sinεcosθ。

聯合式（4）和式（5），整理可得：

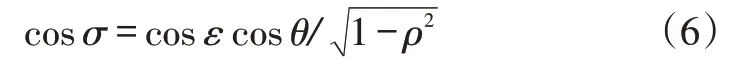
式（6）為斜面角度沿垂直方向投影到水平面的投影方程。設λ1為任意位置車輪軸線與水平面的夾角，則=mcosλ1。所以，根據水平面的△OD1M1（即△O′D′M′），由余弦定理可得：

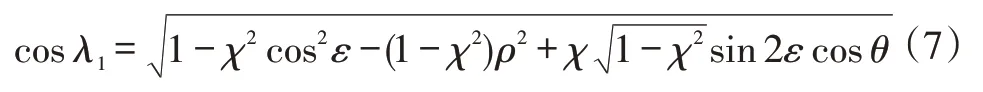
λ1也是文獻[14]中定義的外傾角，考慮了轉向過程中外傾角的變化。由于車輪輪心M與D點的高度差為所以也有：

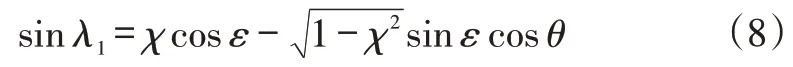
根據△OD1M1各線段長度，有：

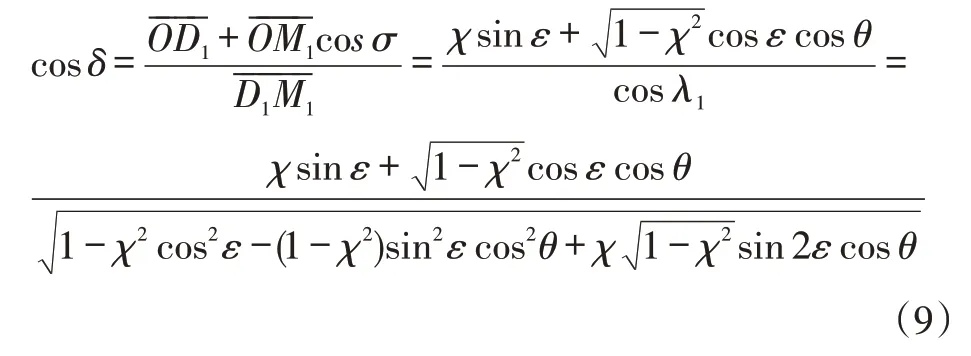
式（9）即為相對主銷垂直面W的主銷轉角水平分量方程，水平分量的角度頂點D′是車輪軸線與主銷軸線共點D在水平面的投影點。由式（9）反求θ：

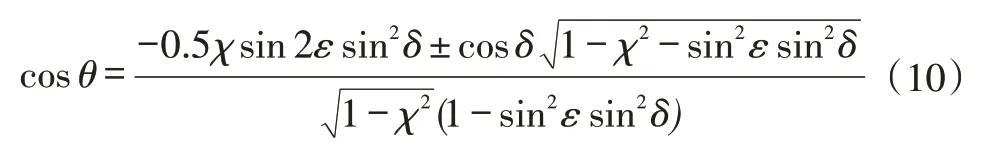
式（10）有2 個解，互為補角，統一取“+”號。式（9）和式（10）即為斜面角度θ與其水平分量δ的相互映射關系式。對圖3所示的右主銷，用同樣的方法可推導出同樣的式（9）與式（10），只需將θ、δ分別用θ′、δ′代替即可。

顯然，δ=f1(θ)、θ=f2(δ)均為變量θ或δ的偶函數，且δ=f1(θ)=f1(360?+θ)=f1(360?-θ)，θ=f2(δ)=f2(360?+δ)=f2(360?-δ)。

利用上述函數特性，可以求出車輪轉角與主銷轉角，即δL和θL、δR和θR的相互映射運動關系式。

2.3 左轉向輪轉角與左主銷轉角的關系

為了考慮主銷后傾及車輪前束對YL軸正向方位的影響，引入2個符號常數：

車輪軸線在初始位置（車輛直行）時，從圖4中可以看出，其在水平面的投影D′M0′與W面的夾角為(δ0-sbτ0)（δ0為主銷軸線在水平面投影與yL軸所夾銳角），按式（10）求出初始位置的θ記為θ0。以(δ0-sbτ0)和θ0為角度參考位置，即可求出δL和θL的關系。

由θL求δL時（稱為左側“銷-輪”轉角計算），先按θ=|sbstθ0-θL|用式（9）求得δ，則：

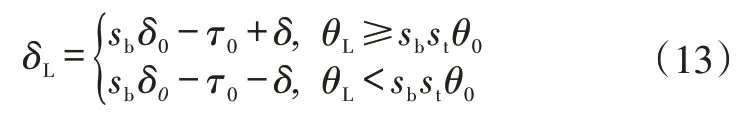
由δL求θL時（稱為左側“輪-銷”轉角計算），先按δ=|-sbδ0+τ0+δL|用式（10）求θ（如果δ＞180°，則θ取反再加360°，即360°-θ)，則：

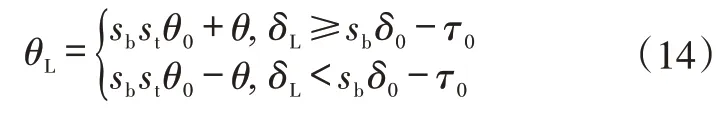
2.4 右轉向輪轉角與右主銷轉角的關系

同理，先以(δ0-sbτ0)替換式（10）的δ求出θ0（左、右輪θ0相等）。以θ′=|sbstθ0+θR|替換式（9）的θ求得δ′。則右側“銷-輪”轉角計算公式為：

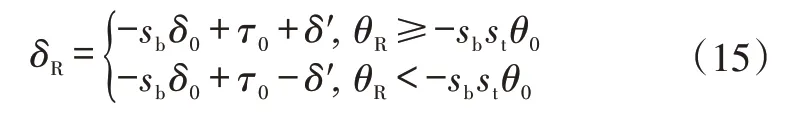
以δ′=|sbδ0-τ0+δR|替換式（10）的δ求出θ′，則右側“輪-銷”轉角計算公式為：

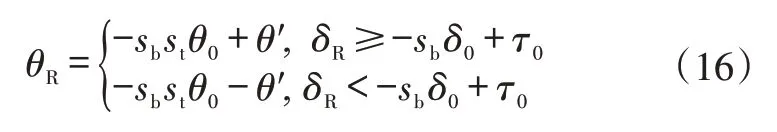
以上公式中，規定δL、θL、δR、θR右轉為正，左轉為負，4 個定位參數按圖1 所示的偏斜方向為正。另外，求得的θL與θR、δL與δR均關于原點對稱。

目前的文獻中“輪-銷”和“銷-輪”的計算模型有3種：多數文獻假設車輪轉角等于主銷轉角（以下稱“等同法”）；文獻[8]、文獻[9]等采用公式，實際就是按主銷單位矢量的垂直分量分解，即θL=δL/(cosα0cosαβ），它是按將角速度分解為水平分量的思路分解的，并不是真正的角度水平分量（以下稱“角速度分量法”）；文獻[10]采用“球面法”。“球面法”被認為是根據主銷轉角計算轉向輪轉角最精確的計算模型。但須注意：文獻[10]中主銷后傾角的定義實際是本文的αβ，與國家標準[14]中的定義不同。

假設車輛4 個定位參數α0、β0、λ0、τ0如表1 所示，其中，δRdmax、δLdmax分別為內、外輪理想最大轉角，分別用“球面法”模型與用本文“銷-輪”模型計算轉向輪轉角值，以比較兩者的差別。

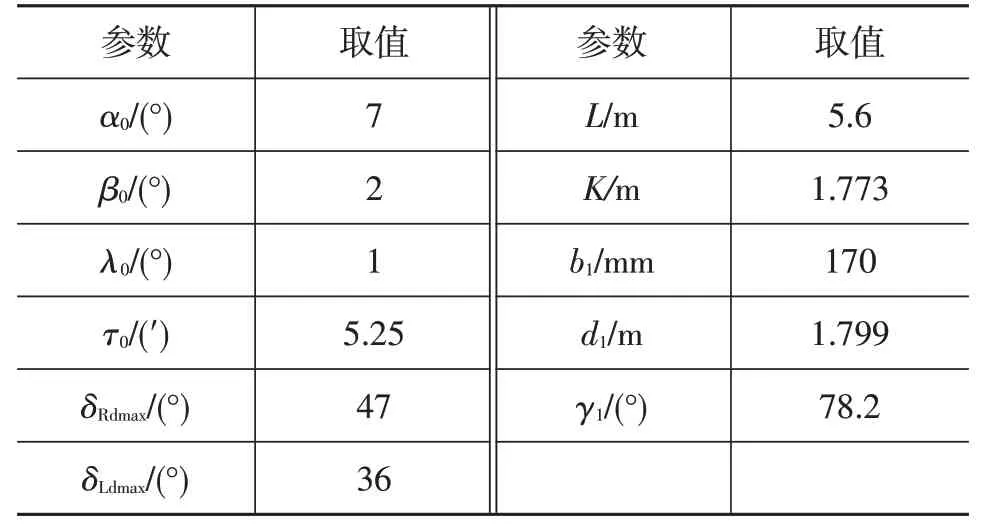
表1 車輛基本特性參數

因左、右側模型計算結果關于原點對稱，這里僅討論右“銷-輪”計算模型。以右主銷轉角θR=-40?～36?為自變量，用各模型計算的右輪轉角用δRi表示（用下標i區分各模型的計算值，i=0 表示本文計算模型，i=1 表示等同法，i=2表示角速度分量法，下同），其他方法與本文模型的差值曲線如圖5所示（其中“球面法”表示左轉的負轉角公式原文獻未提供，為本文增加的）。

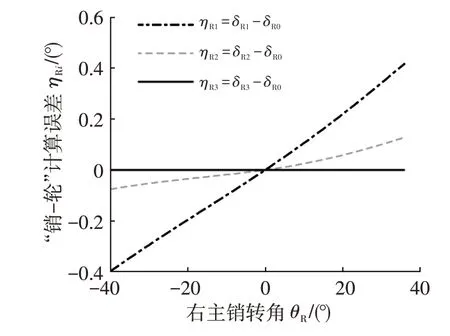
圖5 右側“銷-輪”各計算模型的計算誤差

從圖5 中可以看出，用“球面法”與用式（15）計算的轉向輪轉角的差值接近零（按實際數據查出，在θR=-40°～36°的轉角范圍內，兩者最大差值為0.000 316°）。如果將τ0=0（“球面法”模型沒有考慮前束的影響）代入式（15）中，則兩者沒有差值。

假設各桿件是剛體，不考慮各種力、變形或間隙影響，則車輛的主銷與轉向輪之間的運動轉換關系理論上僅與4 個定位參數有關。本文計算公式中完全考慮了這4個因素，獲得的車輪轉角（δL、δR）是主銷轉角（θL、θR）真正的理論水平分量。

2.5 接地點相對坐標

對左輪（見圖2），當車輪軸位于DM位置時，車輪與地面的接觸點P（假設車輪是剛性的）顯然位于垂直平面DMM′D′與地面水平面的交線D′M′上，且在該面上DM⊥MP。D′M′與軸（與yL平行）的夾角為(δL+τ0)（動態左前束角），故在圖2 的坐標系DxLyLzL中，左車輪接地點P（相對于點D）的坐標為：

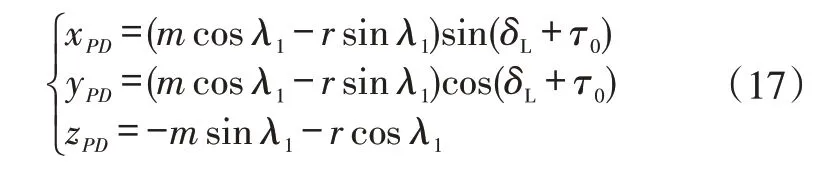
式中，r為車輪的輪輞半徑或取輪胎半徑；λ1的余弦和正弦見式（7）和式（8）。

求解時，左輪以δ=|-sbδ0+τ0+δL|代入式（10）求得θ，再帶入式（7）或式（8）中求出λ1隨車輪轉角的變化規律，然后按式（17）求出P點相對坐標。

用同樣方式可求出右車輪接地點Q相對于點A的坐標（圖3右輪中取yR′∥yR，則A′N′與yR′軸夾角為(δR-τ0)）。

3 轉角誤差及轉角計算誤差

3.1 單側轉向輪轉角誤差計算模型

在優化設計轉向機構時，一般是車輛一側（如左主銷或左車輪）按理想運動輸入，將另一側（如右主銷或右車輪）機構輸出的轉角與理想轉角比較獲得轉角誤差。即：

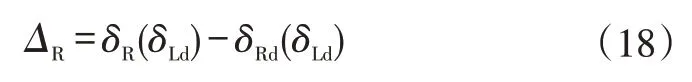
式中，δLd=-δRdmax～δLdmax、δRd分別為左、右輪理想轉角。

功效：滿足人體每天維生素C的需求量。我還可以再加個“天然”、“健康”，又是一副良藥。換成維生素C片同理，其實就是個萬能模板而已。這些維生素C大多屬于保健品，而藥店賣的維生素C則是藥字準，對疾病達到治療作用且合法才能得到這個標識，所以審核很嚴格，幾乎不允許有和治療無關的添加劑混進來。

3.2 轉角的計算誤差

式（18）中的機構轉角δR和理想轉角δRd與計算模型有關，都存在計算誤差的問題。

3.2.1 理想轉角及合理的L、K取值

轉向系統的優化目標是保證左、右輪轉向時的純滾動關系，即δL、δR必須滿足阿克曼理想轉向條件：

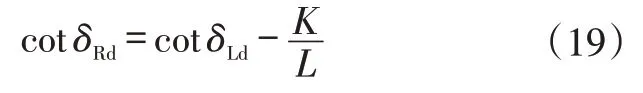
本文同時考慮車輛的左、右轉向，右轉為正，左轉為負，故不再區分內輪、外輪。

式（19）本身是精確的，但其中的L、K有多種定義[12-13]。不合理的定義會造成理想轉角δRd出現計算誤差。

如圖6 所示，要保證轉向輪純滾動，按速度瞬心，左、右主銷軸線與車輪旋轉軸線的交點A、D點在水平地面的投影點與車輪接地點Q、P連線的延長線相交于后軸延長線的O點（水平地面投影點），故有：

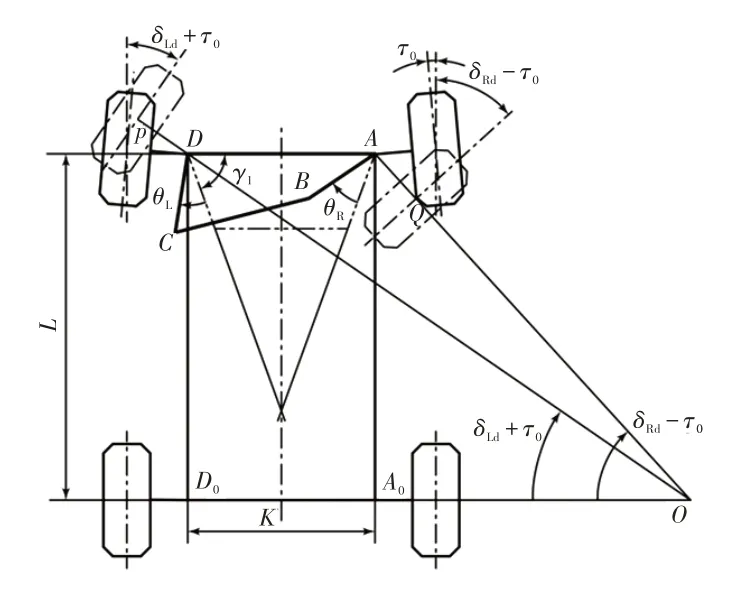
圖6 理想的內、外轉向輪轉角關系

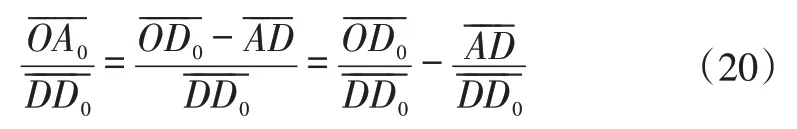
根據式（17），左車輪軸線在水平地面上的投影與橫向（AD線）的夾角為(δLd+τ0)。同樣，右車輪軸線在水平地面上的投影與橫向的夾角為(δRd-τ0)。因此，式（20）可改為：

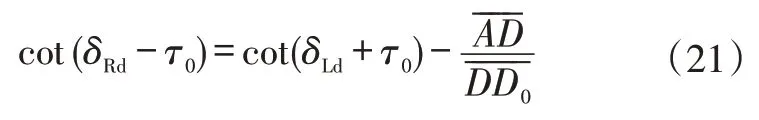
車輪存在外傾導致其產生圓錐滾動，使車輪有向外滾動的趨勢[15-16]。理想情況下，這一趨勢要抵消前束產生的向內滾動，加上考慮到左、右車輪的相互牽制作用，可以消除式（21）中的前束角τ0。對比式（19）與式（21），可得到如下定義：K是兩側轉向車輪軸線與對應主銷的交點之間的距離，即；L是轉向車輪軸線與主銷的交點到過后軸豎直鉛垂面的距離，即

另外，如果假設車輪轉角（δL、δR）等于主銷轉角（θL、θR），從式（17）可知，上述定義依然成立。本文通過轉向車輪接地點分析得到了K和L的理論值，以實現對理想轉角較高精度的計算，而文獻[12]、文獻[13]則用圖形分析或速度分析等方法得到了類似的結果。

3.2.2 轉向機構轉角的計算誤差

單軸轉向機構總轉角計算誤差ηT由3個部分組成：轉向車輪與對應主銷之間轉角模型的計算誤差（分別為“輪-銷”和“銷-輪”計算模型的轉角計算誤差ηL、ηR）和左、右主銷之間的轉角計算模型的計算誤差ηM。

前文已經用“球面法”驗證了本文主銷與轉向輪轉角互算模型的正確性，因此，用前面3 種計算方法獲得的轉角值，減去用本文模型計算得到的轉角值，得到的差值即可認為是各計算模型的轉角計算誤差。因球面法沒有“輪-銷”模型，后文將不再涉及。

第3部分計算誤差ηM與具體機構有關，而且正確的空間模型理論上沒有計算誤差，平面模型與空間模型的差值就是平面模型的計算誤差ηM。

轉向梯形機構設計中，多數文獻采用比較簡單的平面模型[2-3]。而空間模型因推導較為復雜，目前的文獻中沒有明晰的空間梯形機構解析關系式。為便于分析及對比，以下直接列出圖7 所示的空間RSSR（R 表示轉動副，S表示球面副）轉向梯形機構A1BCD1左、右主銷轉向運動關系式：

式中，T=(-1+2 sin2α0sin2αβ)sin(γ1+θL)-sin 2α0sinαβcos(γ1+θL)+d1/b1sinα0sinαβ；U=cos 2α0cos(γ1+θL)-sin 2α0sinαβsin(γ1+θL)-d1/b1cosα0；V=1-2(1-sin2α0cos2αβ)sin2γ1-2 cos2α0cos 2γ1+sin 2α0sinαβsin 2γ1+d1/b1cosα0(2 cosγ1-cos(γ1+θL))+d1/b1sinα0sinαβ(-2 sinγ1+sin(γ1+θL))；γ1為轉向梯形底角；b1為球鉸中心到主銷的垂直距離（A1、D1為垂足），即梯形臂長；為梯形底邊長；為轉向節臂沿主銷軸向偏移的長度。

式（22）有如下的通用解：

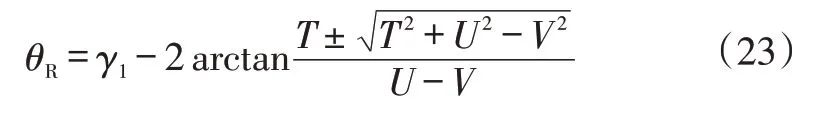
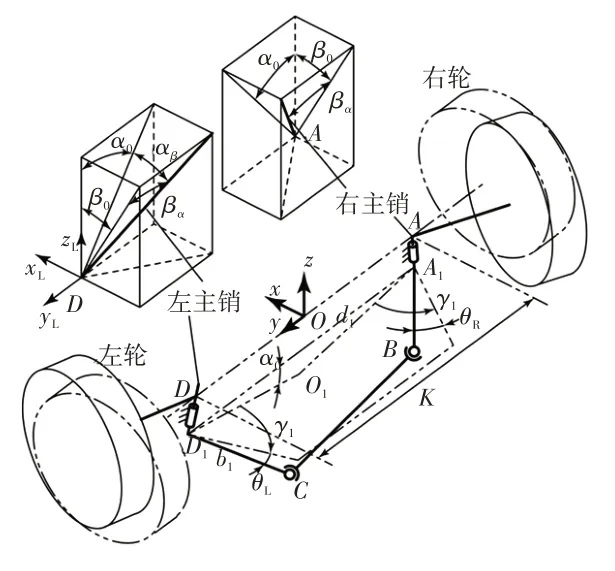
圖7 車輛轉向梯形機構

對于圖7的安裝方式和式（22）中的系數公式，根號前取“-”號。

3.3 實例及討論

假設某型載貨汽車的轉向梯形機構如圖7所示，各參數見表1，分析轉角誤差及轉角計算誤差變化情況。

先觀察轉向輪與主銷互算時的計算誤差ηLi、ηRi。以左車輪轉角δL=-δRdmax～δLdmax為自變量，用各計算模型計算左主銷轉角θLi，差值(θLi-θL0)就是用各模型計算左“輪-銷”轉角的計算誤差ηLi，其隨δL的變化曲線如圖8所示。同樣，用各模型計算的右“銷-輪”轉角計算誤差ηRi隨θR的變化曲線見圖5。表2列出了在整個轉角范圍內ηLi、ηRi的平均值以及最大絕對值。對輕型車輛，一般希望轉向機構的轉角誤差控制在1°范圍以內，相比這個數值，單獨計算的ηLi、ηRi較大。

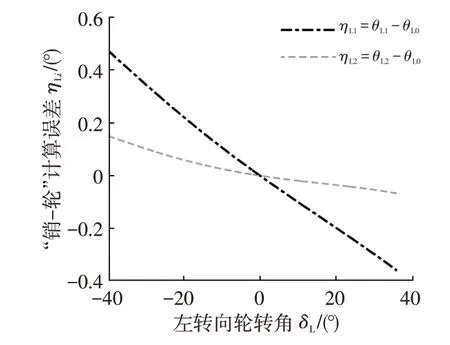
圖8 左側“輪-銷”各計算模型的計算誤差

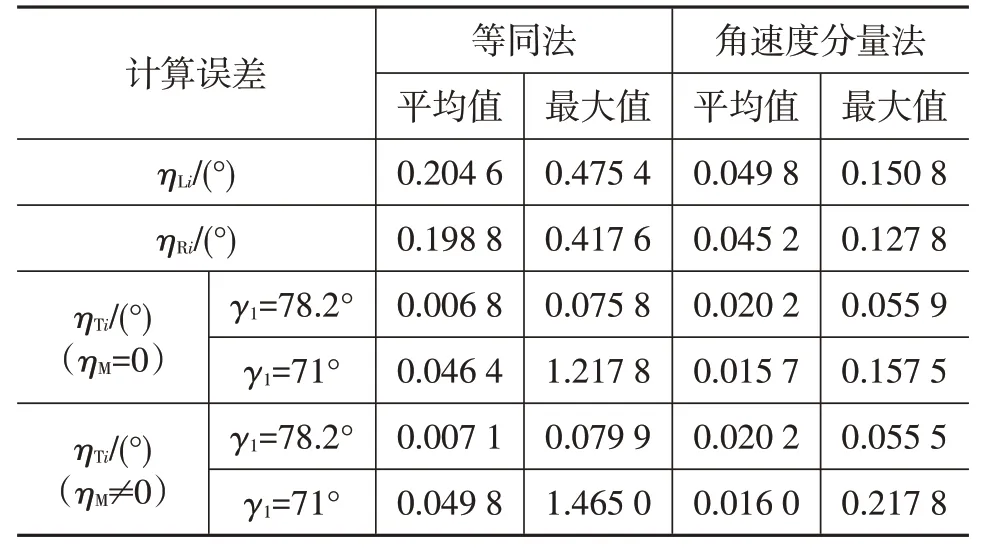
表2 各模型的轉角計算誤差

以δLd求θLi，按轉向機構計算模型式（23）求右主銷轉角θRi，由θRi計算δRi，ηTi=δRi-δR0即為用各計算模型計算的轉向機構總的轉角誤差，其隨δLd的變化情況如圖9 所示，相關值見表2。最后由式（18）求出整個轉向系統的轉角誤差隨車輪轉角變化情況ΔRi，如圖10 所示。實際上，ηM=0時，圖10中ΔR1-ΔR2即可得到圖9的對應曲線。

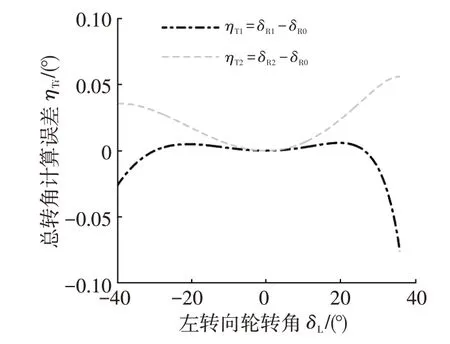
圖9 各計算模型的轉向機構總轉角計算誤差

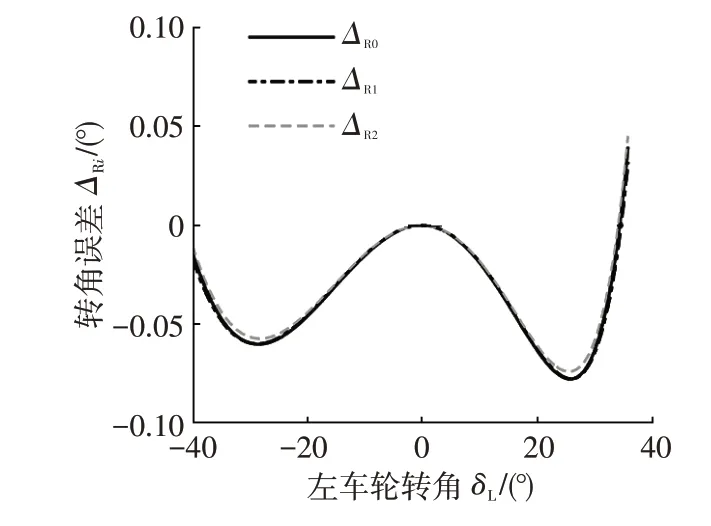
圖10 各計算模型的梯形機構轉角誤差

若主銷之間的轉角計算采用理論上無誤差的空間運動模型式（23），則ηM=0。圖9 及表2 的總轉角計算誤差ηTi（ηM=0）就是左、右兩側主銷與轉向輪之間的計算誤差帶來的。對比圖5 和圖8 可見，將各部分串聯在一起計算后，一般會使總計算誤差ηTi比單獨的轉向輪與主銷互算的計算誤差ηLi、ηRi小。例如，在本例參數及γ1=78.2°下（3 種方法的最大絕對轉角誤差分別為0.442 7°、0.578 0°、0.522 6°，數值較小，表明機構參數比較合理，見圖10），總轉角計算誤差ηTi（ηM=0）平均值及最大絕對值都明顯比左、右側的計算誤差ηLi、ηRi小，特別是“等同法”的誤差平均值反而較“角速度分量法”小。

若將γ1改為71.0°（3種方法的最大絕對轉角誤差分別為12.722 2°、13.782 5°、13.940 0°，數值較大，表明機構參數不合理），左、右側的轉角計算誤差不受影響，總轉角計算誤差平均值雖有變化，但仍比左、右側的計算誤差明顯減小（見表2中γ1=71.0°一行）；這時“等同法”的平均值反而大于“角速度分量法”，而且兩種方法的總轉角計算誤差最大值也反而都大于左、右側的計算誤差最大值。設車輛允許的轉角工作范圍為Ω，總轉角計算平均值減小，表明在Ω的大部分區域，左、右側的轉角計算誤差相互抵消，而最大總轉角計算誤差增大，表明在Ω的小部分工作范圍內，總轉角計算誤差增大。而且該區域一般位于車輛最大轉角附近，這時轉角誤差曲線隨車輪轉角增大而急劇增大。從圖10可以看出，若曲線急劇變化，各模型轉角誤差曲線雖然很接近，但它們之間可能存在較大的轉角差。當然，車輛很少在大轉角區域附近工作，加權優化時一般會弱化該區域計算誤差的影響。

如果將θL=-40°～36°代入有關梯形機構平面模型[2-3]，得到有關ηM值如表3 所示，總的轉角計算誤差見表2中ηTi(ηM≠0)一行。對比表2、表3 可知，計算誤差ηM會不同程度地增大總的轉角計算誤差，但ηM并不是直接疊加在ηTi上。

表3 梯形機構平面模型的轉角計算誤差

可見，由于轉向機構計算誤差函數的特殊性，機構各部分的計算誤差并不是簡單地相互累積增大或相互抵消，它們的變化與機構參數密切相關，但變化規律不明顯。將不精確的計算模型用于設計，其設計精度難以保證。所以，必須慎重使用有計算誤差的運動模型對轉向機構進行優化設計。對重型車輛，若綜合考慮運動副間隙和零件受力變形等因素，直接用主銷之間機構轉角誤差進行優化設計（即“等同法”）可能具有合適的設計精度，但針對輕型和中型車輛設計，建議采用更精確的轉角計算模型進行優化設計或檢驗。

4 結束語

本文采用水平投影方法，獲得了考慮4個定位角參數的主銷轉角與轉向輪轉角相互精確計算的解析式，解決了由車輪轉角計算主銷轉角的問題，得到以下結論：

a.轉向機構設計時，必須考慮轉向輪轉角與主銷轉角的差異，應該使用只有單側轉向輪有轉角誤差的計算方法。在輕、中型車輛的優化設計中尤應考慮采用轉角精確計算模型。

b.機構運動模型帶來的計算誤差對總的轉角計算誤差產生的影響與轉向機構的參數有關。在車輛轉角的很大一部分工作范圍內，當最大轉角誤差較小時，左、右側轉向輪與其主銷之間的轉角計算誤差一般會相互抵消一部分；兩主銷之間的計算誤差會增大計算誤差，但也不是簡單地累加到總轉角計算誤差上。

c.按接地點分析，阿克曼定理中的K值、軸距L值應以車輪軸線與主銷軸線的交點為計算或測量起始點。