多相機非共視場的非合作圓特征位姿測量方法

宋代平，陸 璐

〈測量技術〉

多相機非共視場的非合作圓特征位姿測量方法

宋代平，陸 璐

（重慶大學 機械工程學院，重慶 400030）

以大型光學模塊轉運時基于視覺的位姿測量為背景，利用目標底部同一平面的兩個圓特征，針對大目標近距離對接時的環境限制，提出一種基于距離和角度約束的多相機非共視場位姿檢測方法。對接時球頭與錐孔正確對接，將兩個相機分別固定于球頭機構的內部后采集錐孔邊緣的圓特征，利用非共視場成像的多相機標定獲取兩相機位置關系，融合多個相機的位姿信息，利用兩圓共面和兩相機位置關系約束剔除空間圓位姿解算時的虛假解。實驗驗證了該方法的精度，在1140mm的工作距離時，圓邊緣特征的姿態角誤差小于0.5°，圓心的計算誤差小于1.0mm，實驗結果表明該方法可準確計算位姿，結果可靠有效，在大目標近距離位姿測量時具有明顯實用性。

機器視覺；位姿測量；多相機非公共視場；共面圓特征；距離約束；大目標近距離

0 引言

在激光實驗中，光學模塊的轉運具有潔凈度要求，大尺寸的光學模塊在轉運安裝的過程中，從具有保持潔凈功能的轉運箱到安裝模塊的安裝箱需精密對接，來保證模塊所處環境的潔凈度。轉運箱與安裝箱的對接為近距離自主式對接，而精確的位姿（兩目標間的相對位置）測量是正確對接的關鍵技術。在近距離和超近距離的測量中，基于機器視覺的位姿測量是主要的高精度測量方法之一。現有的視覺位姿測量方法有基于合作目標和非合作目標兩種。基于合作目標的測量法需要靶標上人為設置幾何特征，而且標志器能在單相機或立體視覺相機中完整成像，人為設置的標志點能大大提高目標的檢測精度[1-2]。安裝箱的結構和潔凈度要求，無法安裝測量標志器，只能利用其上的現有特征來完成位姿檢測。大量研究人員對單目非合作目標測量做了研究[3-6]，而非合作目標在自然特征上往往分布不集中，在近距離的工況下更是無法完整成像。模塊安裝箱的底部兩個用于對接的共面錐孔，可作為非合作目標提供空間圓特征和約束條件。單目視覺測量系統[7]結構簡單，但單目在測量位姿時無法獲得深度信息，目前的解決辦法是進行多站測量或給被測目標幾何約束。魏振忠等[8]通過在特征所在平面內的交叉線，根據歐氏空間中交叉線之間的角度不變性作為約束來剔除虛假解；陳至坤等[9]利用工業機器人做已知的平移運動從而有效剔除圓特征目標位姿的虛假解，并通過實驗檢測位姿但精度仍有限；苗錫奎等[10]對非共視場的測量進行了研究，結合手眼相機對不同特征檢測和相機信息融合，提出基于點和直線特征的多相機測量方法，系統引入機械手應用范圍有限，且與基于點特征和直線特征的位姿估計方法[11]相比，基于圓特征的測量在目標識別[12]、定位[13]等領域均有重要應用，圓定位不需要考慮復雜的對應問題，降低算法的難度。

雖然雙目測量系統簡單便捷[14]，但對于很多近距離大目標而且目標特征無法在同一視場成像的場景，無法使用單目視覺給出幾何約束進行測量位姿，也無法通過兩個相機的公共視場立體測距。鑒于此，本文給出一種非共視場圓特征的多相機位姿測量方法。利用多個相機檢測目標上更完整的視覺特征，融合多個相機的特征信息，給位姿檢測提供幾何約束，解出了近距離大目標的位姿參數。

1 多相機位姿解算原理

轉運箱頂部的球頭與安裝箱底部錐孔近距離對接，兩個錐孔的圓邊緣特征始終處于同一平面且間距達1140mm，該方法是針對對接錐孔的圓邊緣特征而設計。利用兩個相機視野內的非合作圓特征完成安裝箱的位姿測量是本方法要解決的問題。

轉運對接測量系統示意圖如圖1，其中包括多相機非共視場測量時的兩相機固定安裝配置方式。安裝箱底部錐孔的邊緣為檢測標志圓和圓，錐孔圓心間距大小為1140mm，相機安裝在球頭內部，定義相機坐標系的、向如圖1所示，原點為相機光心處，向為沿光心垂直圓平面的方向。初定位后滿足圓特征在相機視場成像，本算法的解算結果為球頭與錐孔正確對接時的調整量，實現與目標近距離精確對接。

1.1 坐標系定義及攝像機成像模型

為便于分析，建立如圖2的坐標系：其中A相機坐標系Ca-CaCaCa和像平面坐標系a-aa，B相機坐標系Cb-CbCbCb和像平面坐標系b-bb，世界坐標系W-WWW，單個相機標定之后與世界坐標系的關系確定，可分別在攝像機坐標系下求解出空間圓的支撐平面法向量和圓心坐標。

對于單個相機檢測到的目標上的空間點P，在攝像機坐標系下的坐標表示為(X,Y,Z)，點P通過攝像機鏡頭投影到圖像物理坐標系的坐標為(x,y)，圖像物理坐標與圖像像素坐標(u,v)之間的關系可以表示為：

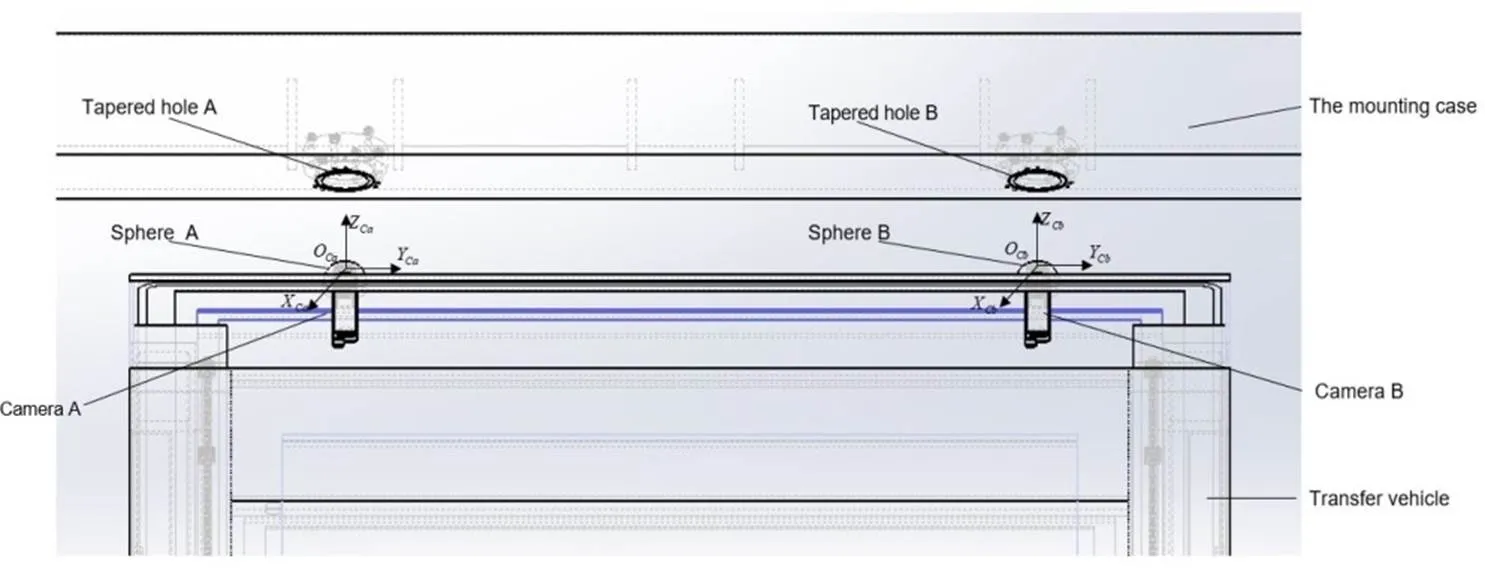
圖1 轉運系統示意圖

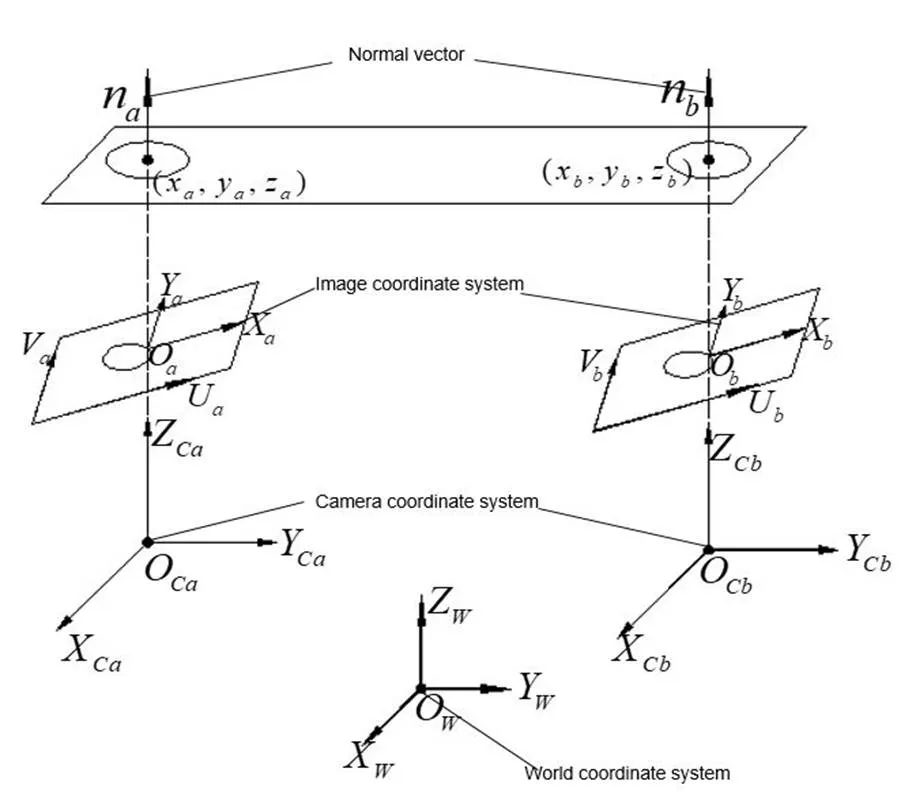
圖2 坐標系定義

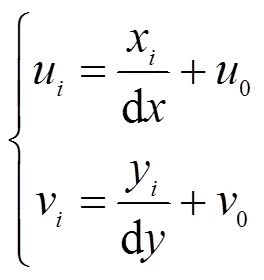
由針孔成像模型和公式(1)，可將圖像像素坐標系和攝像機坐標系間的關系表示為：

式中：為相機的焦距；(0,0)為攝像機成像平面的中心點坐標；d、d為單個像素在方向的尺寸；(0,0,, d, d)為需要通過標定得到的攝像機內參數。

1.2 空間圓參數求解

一般情況（除空間圓成像為直線）下，空間圓形特征投影到圖像坐標系為橢圓，假設圓形特征半徑為，光心與成像橢圓所形成橢圓錐面，若用一個平面去切割該圓錐且截線為半徑的圓平面，此圓環面的中心包含圓特征的位置坐標信息，平面的法向量(n,n,n)包含了圓特征的姿態信息，能確定三維空間中的圓形姿態的2個自由度（圓形特征圍繞著過其圓心的法向量旋轉具有對稱性），即俯仰角和偏轉角。其中俯仰角定義為法向量與XOY平面的夾角，偏轉角為法向量在XOY上的投影線與軸正方向的夾角。根據數學計算有

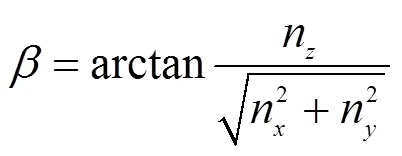
某位置的圓特征在圖像物理坐標系投影成像為橢圓，通過圖像處理可以獲取該橢圓投影的方程：

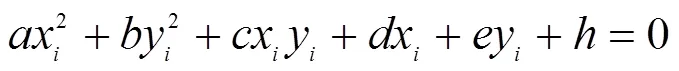
而攝像機的針孔成像模型為：

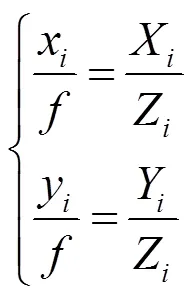
聯立公式(5)、(6)可獲得光心與成像橢圓所形成的橢圓錐的方程：

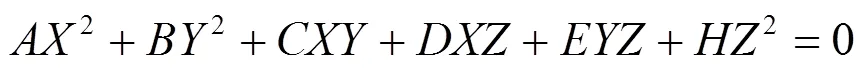
將式(7)用二次型表示為：

由矩陣知識可知必為實對稱陣，必然可對角化，即存在矩陣，使得：

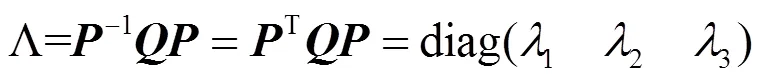
其中為：

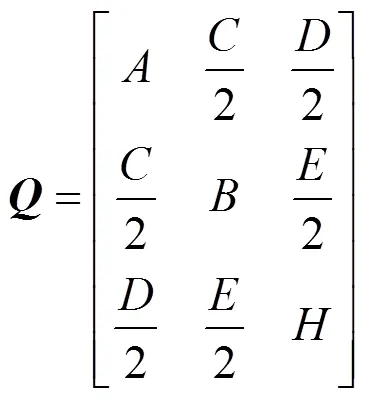
為了避免在攝像機坐標系進行復雜計算，故將其變換到標準坐標空間進行描述和計算，便于清晰表達位姿參數，解算出結果后需再變換回攝像機坐標系。

故令[]T＝[￠￠￠]T，并將此變換帶入到式(8)可以得到標準二次型：

[￠￠￠]－1[￠￠￠]T＝0 (11)

即把橢圓錐方程變換到以￠為旋轉軸的標準坐標系中：

1￠2＋2￠2＋3￠2＝0 (12)

式中：由標準橢圓錐的性質，1、2、3中必有2個值符號一樣且與另一個相反。因此可以求得圓特征在標準坐標系下圓的支撐平面過圓心的法向量(n￠,n￠,n￠)和圓心坐標[x￠,y￠,z￠]分別為：

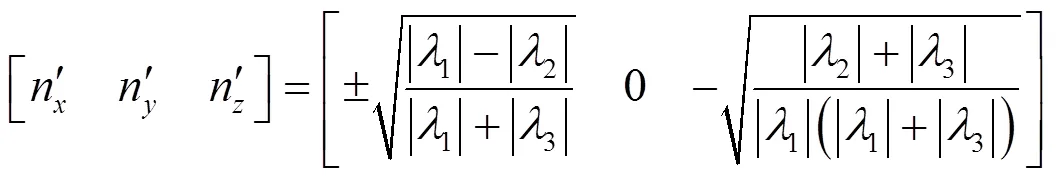
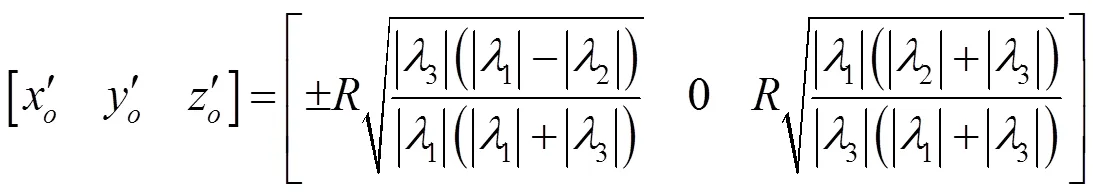
最后變換到攝像機坐標系下：

[xo yo zo]T＝P[xo￠yo￠zo￠]T (15)

[nxnynz]T＝P[nx￠ny￠nz￠]T (16)

1.3 多相機位姿測量原理

由1.2節的分析可知，在沒有約束的條件下，一個相機成像的圓在位姿解算時得到了兩組解，在大目標近距離的工況下，單個相機很難同時采集有效的特征和約束信息，故本文提出用兩個非共視場的相機分別采集兩個圓特征，提供距離和角度約束消除虛假解。

在大目標近距離測量時，可供檢測的非合作目標的特征距離遠，兩個相機無法形成公共視野，因此無法使用立體標定[15]得到兩個相機的相對位置。非公共視場的雙目標定方法較多[16-17]，由于標定結果對最終的位姿測量結果影響較大，為盡量減小誤差，本文選用特制標定板標定A、B相機的位置關系，以保證標定精度，如圖3。本文采用的雙目標定步驟為：

1）首先對A相機精確單目標定后，可以得到A相機外部參數的旋轉矩陣a和平移矩陣a；然后對B相機精確單目標定，獲得外部參數的旋轉矩陣b和平移矩陣b。

2）選擇滿足同時在A、B相機上成像的標定板，同時采集圖像，分別選取A、B相機圖像上檢測到的最左上角的角點，在標定板確定兩個角點的實際位置。

3）利用標定板上兩個角點間已知的的平移向量，計算A相機和B相機之間固定的旋轉矩陣AB和平移矩陣AB。

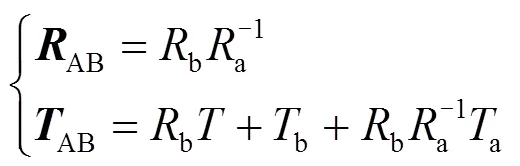
由公式(15)、(16)可分別求解出兩個圓在A相機坐標系下的圓心坐標a￠和法向量a￠，在B相機坐標系下的圓心坐標b(b,b,b)和法向量b。通過ab和ab坐標轉換，將A相機坐標系C1-C1C1C1轉換到B坐標系C2-C2C2C2下后得圓A的圓心坐標a(a,a,a)和法向量a，由于兩個系相機所拍攝圓邊緣特征處于同一支撐平面，則兩個圓特征的法向量平行，a、b同在坐標系C2-C2C2C2下時：

a＝×b（其中為非零常數） (18)

由公式(3)、(4)、(13)可解算出兩組相同的姿態角，即真實姿態角。由公式(14)可知，圓心a和b均有兩組解，而兩圓心構成的固定的空間向量ab為(000)T，假設a、b在坐標系C2-C2C2C2下的坐標分別為(a,a,a)、(b,b,b)，可通過約束來剔除虛假解：

以上引入多相機約束，利用特殊標定和非合作標志的圓特征，解算出了大目標近距離條件下的非共視場多相機對接所需的移動量和姿態角。

2 實驗驗證與結果分析

2.1 實驗與結果

為了驗證算法的有效性和可行性，建立了基于模擬圓邊緣的位姿測量實驗臺。實驗臺主要包括模擬對接機構中的兩個參數相同的圓特征，兩個工業相機和相機支架，標定板和激光跟蹤儀和計算機。采用Visual Studio2013作為編譯器，編程語言為C/C＋＋，標定板為1300mm×200mm的棋盤格（單格20mm×20mm），模擬的錐孔圓邊緣的直徑為60mm，尺寸精度為0.05mm，兩個共面圓的平面度誤差為0.1mm，兩個圓邊緣圓心的距離為1140mm。相機使用的Basler的acA1600-20GM，分辨率1626pixel×1236pixel，配Space Vision焦距4mm的定焦鏡頭，實驗之前對兩個相機分別精確標定，參數見表1。

表1 相機參數表

實驗中，首先利用特制標定板對兩個相機的位置標定。兩個圓分別在兩個相機的視場內完整成像時，檢測各相機拍攝到的圓。對兩個非共視場的相機拍攝的不同的圓特征圖像，分別進行高斯平滑、降噪等預處理，然后通過閾值分割得到感興趣區域、邊緣檢測，最后用橢圓擬合得到亞像素的橢圓點集。通過Opencv和數學計算可擬合出圖像坐標系下的標準橢圓方程，最終擬合出攝像機坐標系下橢圓方程用于解算位姿。橢圓擬合實驗如圖4所示。

實驗中用激光跟蹤儀測量圓特征的位姿作為準確值，激光跟蹤儀測量圓平面所在的白色矩形輪廓的位姿，矩形與圓邊緣的位姿精確已知，所以利用激光跟蹤儀可以間接求出兩個圓的法向量和圓心位置。根據提取的橢圓和多相機約束求解位姿結果，將結果與激光跟蹤儀的準確值對比。表2為3個不同位置時的姿態角的測量結果，姿態角分別為俯仰角和偏航角，單位為度；表3為3個不同位置時兩個圓心的坐標測量結果，圓心坐標分別為A(Oa,Oa,Oa)和B(Ob,Ob,Ob)，AB之間的差值為向量AB，單位為mm；實驗中每個位置采集20組圖，取計算結果的平均值作為位姿檢測結果，求得計算檢測結果相對于準確值的平均誤差。

由表2可知，實驗的3個不同位置中，同一位置時圓的兩組姿態角測量結果中有一組姿態角近似相同且與接近精確值，可以成功剔除另一組虛假解。保留的正確的姿態角結果與精確值的平均誤差在0.5°以內。由表3可知，兩個圓心的兩組平移量結果，有一組值兩個圓心的空間距離與精確值基本相同，能正確篩選出真實解，其中真實的位移計算結果與精確值的平均誤差在1.0mm以內，表明了本方法的真實有效性和檢測精度，滿足模塊轉運時對位姿的檢測要求。

圖4 實驗圖片處理過程圖

2.2 誤差分析

根據實驗的測量值與精確值的差異分析，測量誤差主要來源于：

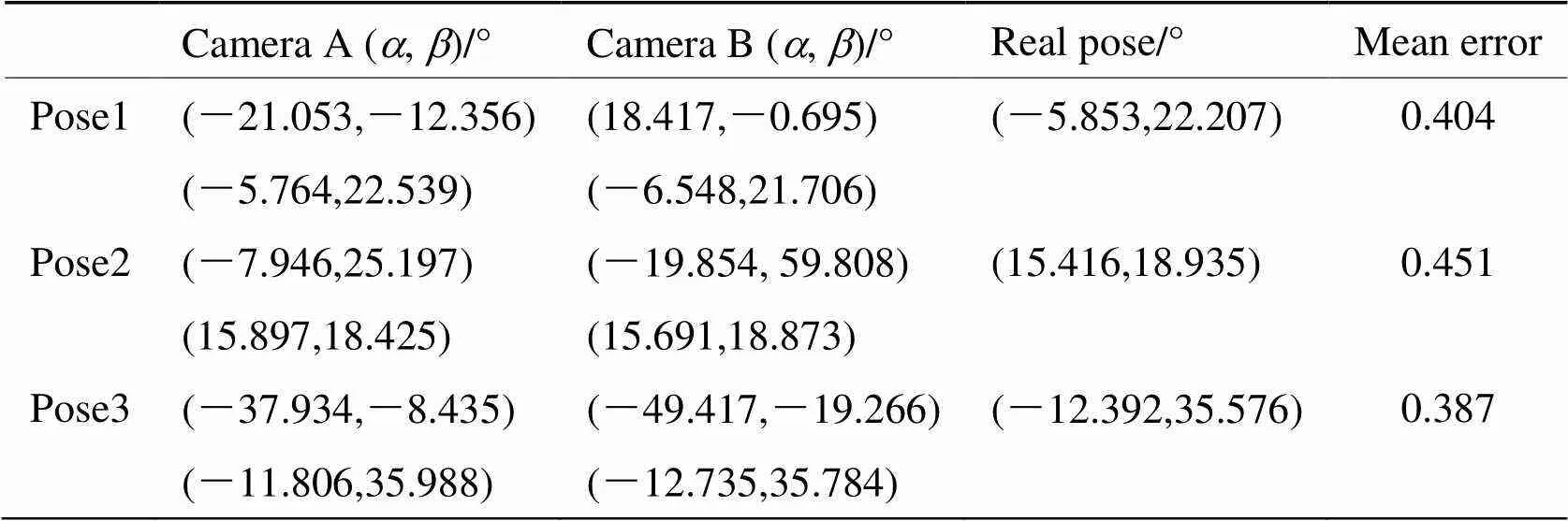
表2 姿態角計算結果

表3 平移量計算結果

1）相機標定時的參數誤差。A、B相機單目標定時的內參數和外參數無法避免地產生誤差。內參數誤差會影響特征圓和特征角點的成像精度，外參數不僅影響到圖像坐標系轉換到空間坐標系的位姿，也會影響到本文提出的雙目標定方法的精度。

2）橢圓擬合精度產生的誤差。準確地擬合出橢圓是精確獲取橢圓在圖像坐標的參數，橢圓參數的精度會直接影響位姿計算精度。

針對以上誤差來源，在后續的研究過程中主要在以下方面進行改進：

3）提高相機標定的精度。研究高精度的非線性標定方法，對相機的畸變系數進行標會在一定程度上提高標定精度。

4）提高特征點的提取精度。橢圓上特征點直接影響到橢圓擬合，進而影響最終的位姿準確度。后續需要研究高精度的特征檢測算法和優化橢圓擬合算法。

3 結論

本文提出了基于非共視場多相機的大目標近距離位姿檢測方法，分別用兩個相機檢測對接目標上同一平面上無公共視野的一對圓特征，利用圓心的固定距離和同一平面相同的姿態角剔除虛假解。本方法充分利用球頭機構的內部空間和錐孔的圓邊緣特征，獲取更多的目標信息，無需附加其他標志物，便于工程實施。實驗結果驗證了方法的正確性和實用性，并具有一定的穩定性。在1140mm的工作距離時，位移的計算誤差在1.0mm內，姿態角誤差在0.5°以內，滿足大目標近距離對接時位姿檢測的精度要求。

[1] Eberli D, Scaramuzza D, Weiss S, et al. Vision Based Position Control for MAVs Using One Single Circular Landmark[J]., 2011, 61(1-4):495-512

[2] 王天宇, 董文博, 王震宇. 基于單目視覺和固定靶標的位姿測量系統[J]. 紅外與激光工程, 2017, 46(3): 146-153. WANG Tianyu, DONG Wenbo, WANG Zhenyu. Position and attitude measurement system based on monocular vision and fixed target[J]., 2017, 46(3): 146-153.

[3] 苗錫奎, 朱楓, 丁慶海,等. 基于星箭對接環部件的飛行器單目視覺位姿測量方法[J]. 光學學報, 2013, 33(4):123-131. MIAO Xikui, ZHU Feng, DING Qinghai, et al. Measurement method of aircraft monocular visual pose based on star-arrow docking ring component[J]., 2013, 33(4): 123-131.

[4] 張麗敏, 朱楓, 郝穎明,等. 基于圓特征和異面點特征的位姿測量[J]. 光子學報, 2015, 44(11):83-88. ZHANG Limin, ZHU Feng, HAO Yingming, et al. Posture measurement based on circular and non-planar features[J]., 2015, 44(11): 83-88.

[5] 孫增玉, 高越. 基于視覺技術的非合作航天器相對位姿測量方法[J]. 宇航計測技術, 2017. 37(4): 1-6. SUN Zengyu, GAO Yue. Measurement method of relative position and attitude of non-cooperative spacecraft based on vision technology[J]., 2017, 37(4): 1-6.

[6] ZHENG Yinqiang, MA Wenjuan, LIU Yuncai. Another way of looking at monocular circle pose estimation[C]//, 2008: 861-864.

[7] 趙連軍, 劉恩海, 張文明, 等. 單目三點位置測量精度分析[J]. 光學精密工程, 2014, 22(5): 1190-1197. ZHAO Lianjun, LIU Enhai, ZHANG Wenming, et al. Accuracy analysis of single-eye three-point position measurement[J]., 2014, 22(5): 1190-1197.

[8] 魏振忠, 趙征, 張廣軍. 空間圓姿態識別二義性的角度約束消除[J]. 光學精密工程, 2010, 18(3):685-691. WEI Zhenzhong, ZHAO Zheng, ZHANG Guangjun. Elimination of angle constraints on ambiguity of space circular attitude recognition[J]., 2010, 18(3): 685-691.

[9] 陳至坤, 胡連軍, 王一, 等. 基于角度約束的目標位姿測量二義性剔除方法[J].應用光學, 2018(1): 107-111.CHEN Zhikun, HU Lianjun, WANG Yi. A method of eliminating ambiguity in target pose measurement based on angle constraint[J]., 2018(1): 107-111.

[10] 苗錫奎, 朱楓, 郝穎明. 多像機非共視場的非合作飛行器位姿測量方法[J]. 紅外與激光工程, 2013, 42(3):709-715.MIAO Xikui, ZHU Feng, HAO Yingming. Pose measurement method for non-cooperative space vehicleusing multiple non-overlapping cameras[J]., 2013, 42(3): 709-715.

[11] 尚洋, 孫曉亮, 張躍強, 等. 三維目標位姿跟蹤與模型修正[J]. 測繪學報, 2018, 47(6): 113-122.SHANG Yang, SUN Xiaoliang, ZHANG Yueqiang, et al. 3-D target pose tracking and model modification[J]., 2018, 47(6): 113-122..

[12] 宋文杰, 付夢印, 楊毅. 一種面向無人駕駛汽車的高效交通標志識別方法[J]. 機器人, 2015, 37(1): 102-111. SONG Wenjie, FU Mengyin, YANG Yi. An efficient traffic sign recognition method for driverless vehicles[J]., 2015, 37(1): 102-111.

[13] 王憲, 趙前程, 譚建平. 應用區域估計的復雜背景多圓快速定位方法[J]. 中南大學學報: 自然科學版, 2016, 47(7): 2266-2272. WANG Xian, ZHAO Qianjin, TAN Jianping. Fast multi-circle location method using complex background of regional estimation[J]., 2016, 47(7): 2266-2272.

[14] 付朋, 陳新度, 吳磊. 基于角點的雙目視覺絕對定位研究[J]. 電子測量與儀器學報, 2018, 32(3): 1-8 FU Peng, CHEN Xindu, WU Lei. Research on absolute positioning of binocular vision based on corner[J]., 2018, 32(3): 1-8.

[15] 郭清達, 全燕鳴, 于廣平, 等. 基ICP算法的雙目標定改進方法研究[J]. 光學學報, 2016(12): 198-205. GUO Qingda, QUAN Yanming, YU Guangping, et al. Base ICP algorithm for double target determination[J]., 2016(12): 198-205.

[16] TANG Yiping, ZHOU Jingkai, XU Haitao, et al. A novel laser vision sensor for omnidirectional 3D measurement[J]., 2013, 45: 1-12.

[17] XIE Meng, WEI Zhenzhong, ZHANG Guangjun, et al. A ?exible technique for calibrating relative position and orientationof two cameras with no-overlapping FOV[J]., 2013, 46: 34-44.

Non-cooperative Circle Characteristic Pose Measurement Using Multiple Cameras without Public Field of View

SONG Daiping，LU Lu

(College of Mechanical Engineering, Chongqing University, Chongqing 400030, China)

Based on vision-based pose measurement during the trans-shipment of large optical modules, a non-public field of view(FOV) pose detection method for multi-cameras based on distance and angle constraints is proposed in this study.The method is developed by using two circular edges of the same plane at the bottom of the target of the installation module to eliminate the environmental constraints of close-range docking of large objects. While docking, the sphere of the transfer vehicle was correctly docked with the target cone hole. The two cameras were fixed in the hole of the sphere, and the circular features of the edge of the cone hole were collected. The position relationship between two cameras was obtained by multi-camera calibration in non-public FOV study on non-cooperative circle characteristic pose measurement using multiple cameras without public FOV imaging and the position and altitude information of multiple cameras were confluent. Finally, the false solutions in the pose calculation were eliminated using the constraints of two coplanar circles and two cameras' position relations. The experimental results show that the method can accurately calculate the pose. The calculation process is concise, and the results are reliable and effective. The error of the attitude angle of the circular edge feature is less than 0.5 degrees, and the calculation error of the center of the circle is less than 1.0mm at a working distance of 1140mm. The proposed method has practical applications in measuring the position and altitude of large targets within close range.

machine vision, pose measurement, multi-camera non-public FOV, coplanar circle feature, distance constraint, close large target

TN209；TP242

A

1001-8891(2020)01-0093-06

2019-07-01；

2019-12-31.

宋代平（1978-），男，四川綿陽人，副教授，博導，博士，主要從事機械設計、機器視覺及應用等研究方向。E-mail: songdp@cqu.edu.cn。

國家自然科學基金聯合基金項目（U1530138）。