求解偽單調型變分不等式的一種投影算法
陳 園, 何詣然
(四川師范大學 數學科學學院,四川 成都610066)
設F 是Rn→Rn的一個連續映射,C 為Rn 的一非空閉凸子集.本文考慮經典的Hartman -Stampacchia變分不等式問題:求x*∈C使得
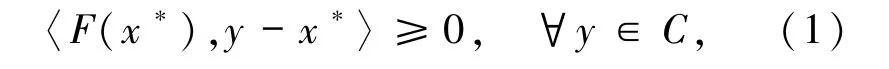
其中〈·,·〉是歐幾里德內積.
變分不等式在經濟、交通等領域中有著廣泛的應用.關于用數值迭代法求解變分不等式的研究,已有著豐富的成果[1-12].投影算法是求解單調型變分不等式的主要算法,削弱變分不等式單調性假設條件是研究變分不等式的重要內容.文獻[3]中的算法3.2 及文獻[11]中第72 頁的算法,為敘述簡便將其分別記為算法1 和2,具有以下的迭代形式:
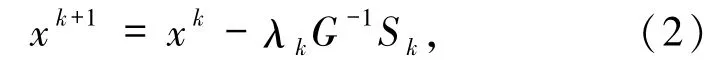
其中λk是嚴格大于0 的步長,G 是一對稱正定矩陣,Sk是第k次迭代步選取的迭代方向.近年來,關于(2)式的算法研究可參見文獻[13 -19].為使算法簡潔,將對稱正定矩陣G取為單位矩陣.
算法1 在每一步迭代中,通過Armijo 線性搜索
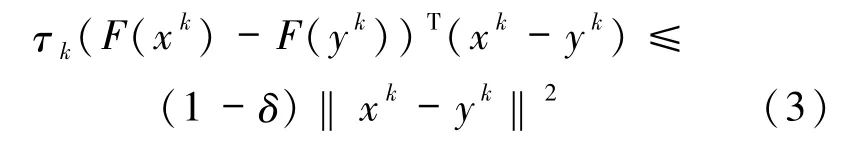
確定τk,令

其中τk=αnkτk-1,nk是滿足(3)式成立的最小非負整數,α∈(0,1),τ -1∈(0,∞),
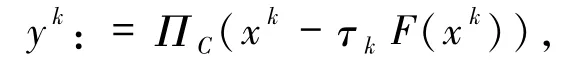
ΠC(x)表示x到閉凸集C上的投影,θ∈(0,2),δ∈(0,1).該算法在F 為單調連續映射且(1)式有解的條件下是全局收斂的.
算法2 在每一迭代步中,使用(3)式的Armijo線性搜索,并令
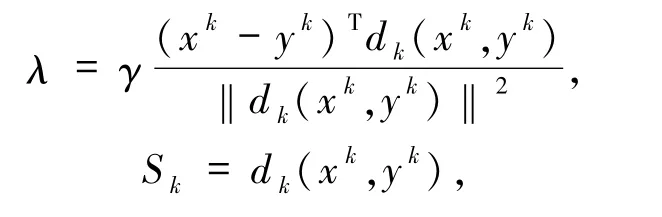
其中
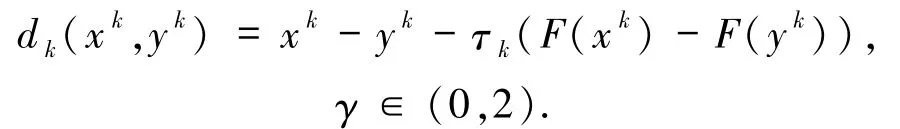
該算法在F 為單調連續映射且(1)式的解集非空的條件下是全局收斂的.
注意到算法2 的迭代步,由
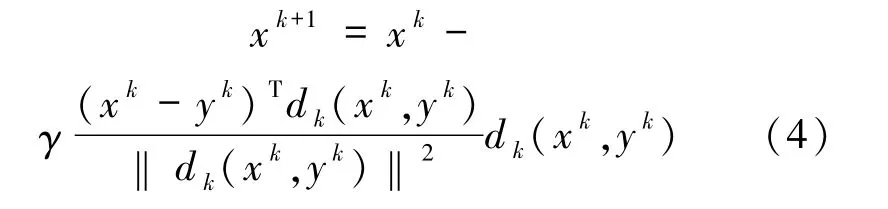
易得,xk+1恰為xk在超平面
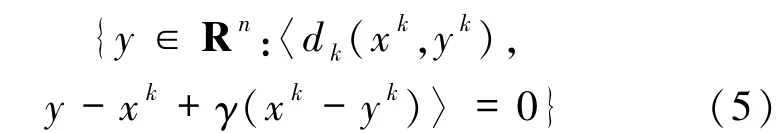
上的投影.本文令γ∈(0,1],τk:=αnk,α∈(0,1),通過(5)式中的超平面,證明了當變分不等式(1)的解集非空且F 為偽單調連續映射時,所提算法3.1 是全局收斂的,其中nk是滿足(3)式成立的最小非負整數.
近20 年來,已有較多的文獻研究了用投影型算法求解偽單調型變分不等式問題,如文獻[4 -9].為后文敘述方便,對任意一個正實數μ,任意x∈Rn,記rμ(x)=x -ΠC(x -μF(x)).文獻[4 -9]中共使用了2 種與(3)式不同的Armijo 線性搜索.文獻[4,6,8]中使用了Armijo線性搜索
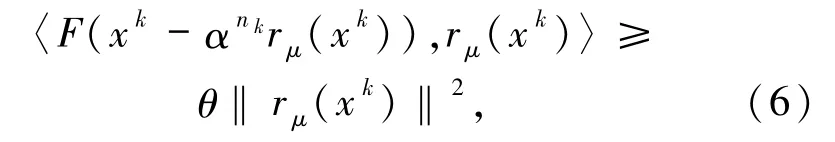
而文獻[5,7,9]中使用的Armijo線性搜索為
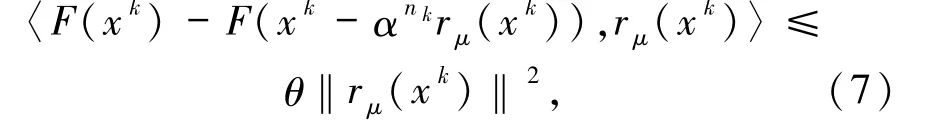
其中α∈(0,1),θ與μ均為正數且取值相關,nk是滿足不等式(6)或(7)成立的最小非負整數.易得,在每次迭代中Armijo線性搜索(6)與(7)式較之于(3)式,計算投影算子的次數更少,事實上使用(3)式,每一次nk取值的變動將計算一次投影算子.本文中使用的Armijo 線搜索與(6)和(7)式雖不同,但可以將文獻[4 -9]及本文中的算法獲得下一迭代步xk+1的步驟統一為如下形式:
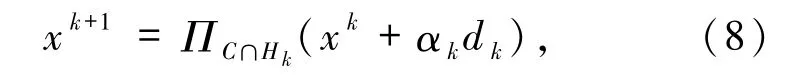
其中Hk為某超平面或半空間,αk為第k 步的步長,dk為第k步的迭代方向.則文獻[4,7 -9]中的算法對任意非負整數k,αk=0,文獻[4,8]的
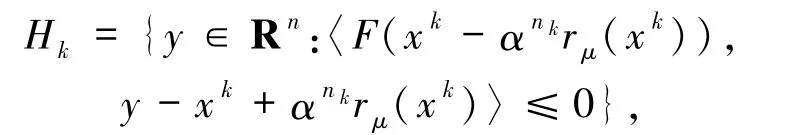
文獻[7,9]中的算法4 的
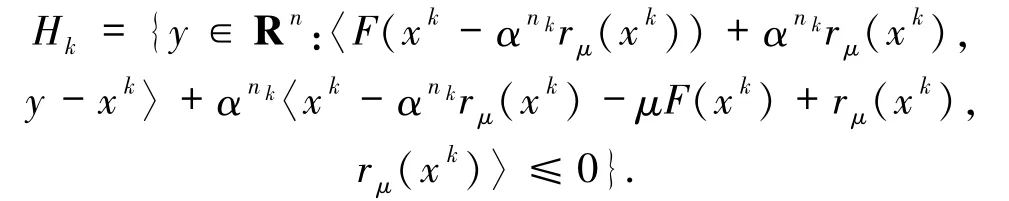
文獻[6]中算法對任意非負整數k,Hk為全空間Rn,
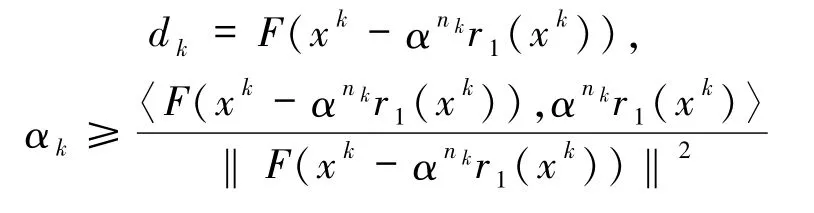
且需滿足
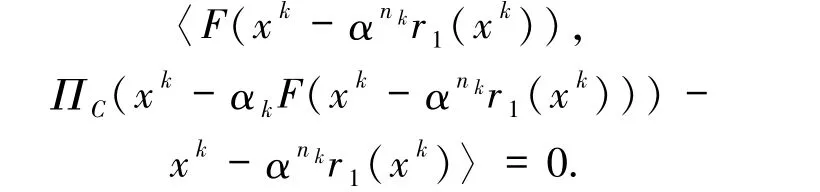
文獻[5]中算法NVE-2 的
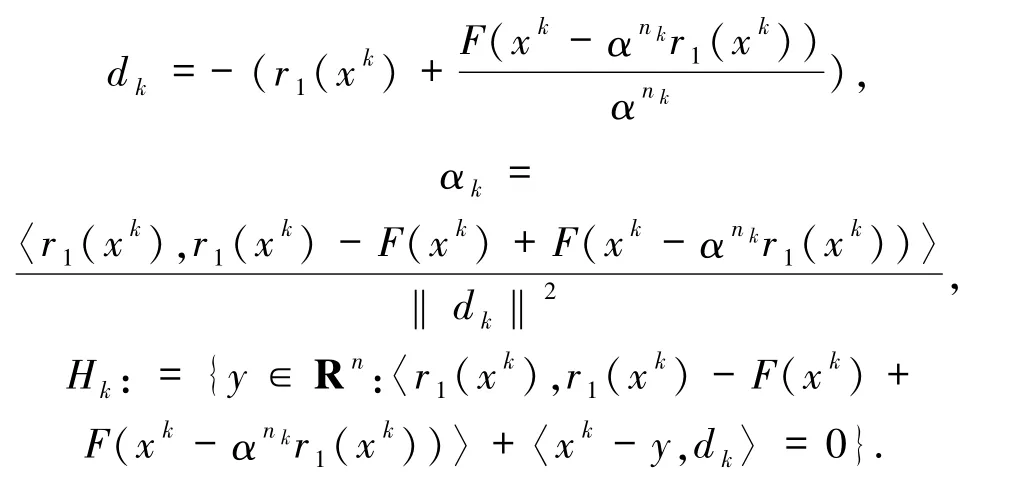
而本文算法在生成下一迭代步xk+1時,對任意非負整數k,
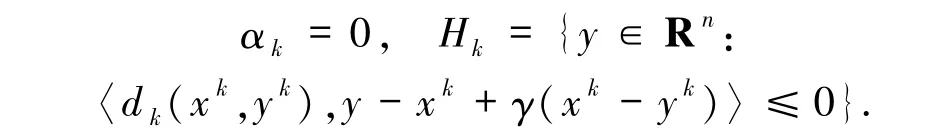
文獻[10]的算法1 使用了與(3)、(6)和(7)式形式均不同的Armijo線性搜索
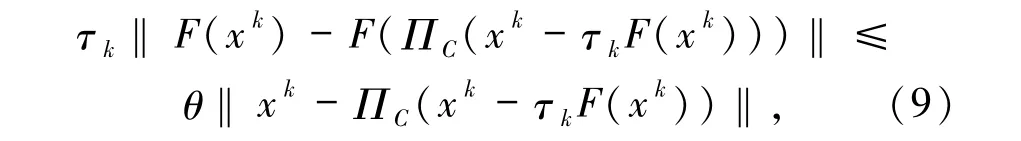
且生成下一迭代步xk+1的等式形如(2)式,該算法的
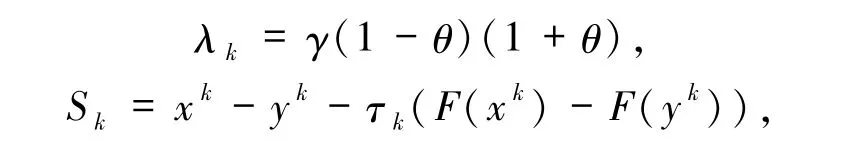
其中
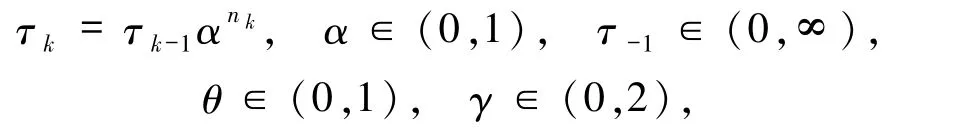
nk是使(9)式成立的最小非負整數.易知(9)式的Armijo線性搜索較之于(6)和(7)式,在每次迭代中仍可能計算更多次的投影算子.本文引理2.1 的證明中指出了它與Armijo 線性搜索(3)式的關系,該算法在F 為偽單調連續映射且(1)式的解集非空的條件下,全局收斂.
為書寫簡潔,將文獻[7]的算法1. 1 與文獻[10]的算法1,分別記為算法3 和4.雖然本文算法2.1 中的Armijo線性搜索較之于(6)和(7)式,在每次迭代中可能計算更多次的投影算子,但不失為一種新的投影型算法,且本文關于例3.1 的數值計算結果可說明,在求解某些變分不等式問題時,本文算法2.1 比算法1 ~4 收斂得更快.記問題(1)的解集為S,本文始終假定S≠?,F為偽單調連續映射.



3 數值實驗
本節給出數值實驗,在Windows 10,處理器為Intel(R)Core(TM)i5 -3317UCPU@1.70GHz的系統環境下,使用版本為R2015b,優化工具為toolbox 7.3 的MATLAB 進行數值實驗.在計算過程中,允許誤差為ε =10-8,即當‖r1(xk)‖2≤10-8程序終止.令算法2.1 中參數取為:τ0=1,δ =0.2,α =0.5,γ =0.8,并將其與算法1 ~4 比較,其中算法1的參數取值為τ -1=1,θ =1.5,δ =0.1,α =0.3;算法2 的參數取值為γ =1.5,α =0.5,δ =0.2,τ -1=1;算法3 中參數的取值為α =0.5,θ =4,μ =0.2;算法4 中G取單位矩陣,α -1=1,α =0.5,γ =1.5,θ =0.5.令x0代表初始點,nf表示計算f的次數,i表示程序迭代的次數,t代表程序運行所需的時間,x 表示最后一個迭代點.
例3.1 令C =[10,20],F(x)=x3,則F(x)在C上是單調映射,易得10 是該變分不等式問題的解,將算法2.1 與算法1 ~4 進行比較,得到的數值結果如表1 ~4 所示.
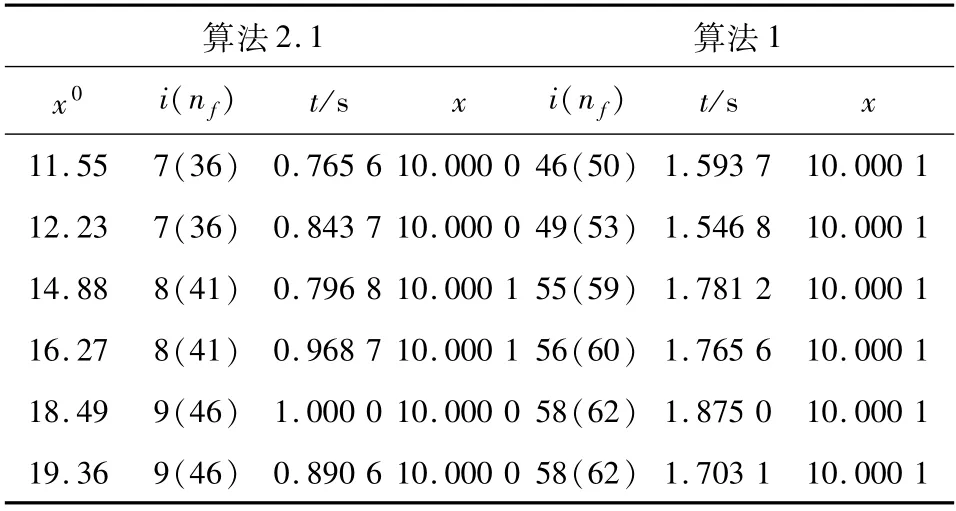
表1 例3.1 的數值結果Tab. 1 Numerical results of example 3.1
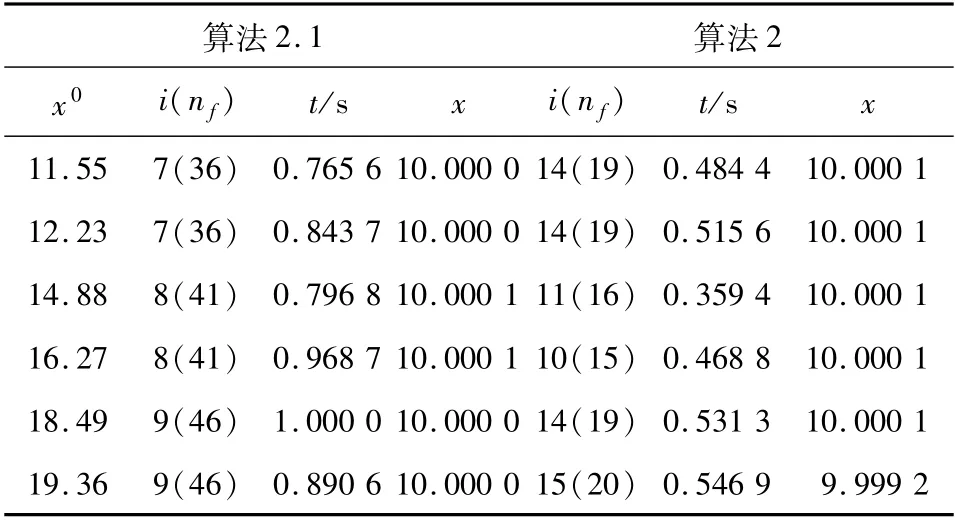
表2 例3.1 的數值結果Tab. 2 Numerical results of example 3.1
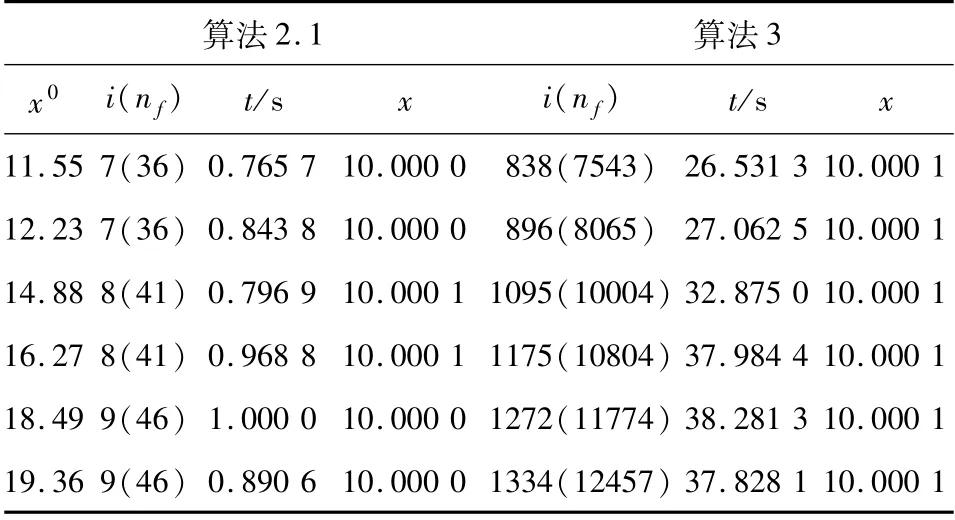
表3 例3.1 的數值結果Tab. 3 Numerical results of example 3.1
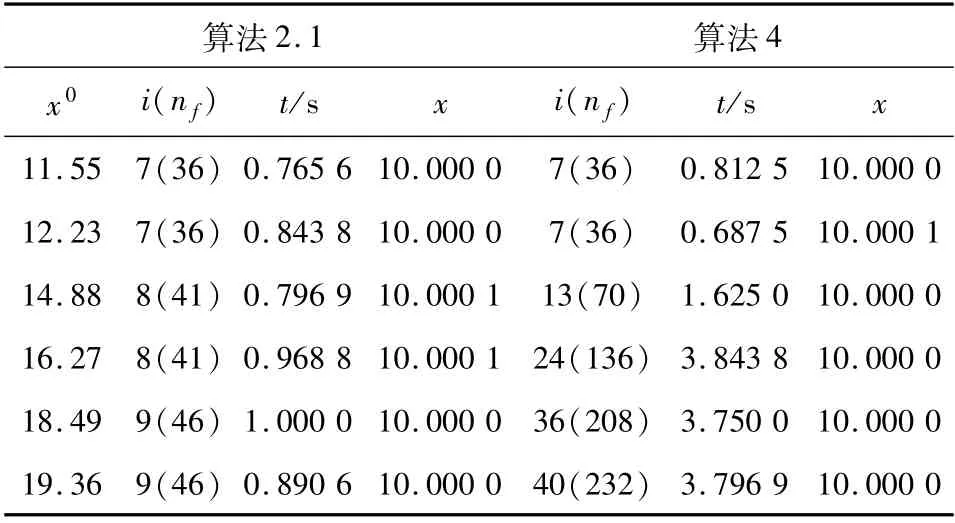
表4 例3.1 的數值結果Tab. 4 Numerical results of example 3.1
4 結論
本文算法2.1 可用于求解偽單調型變分不等式.在例3.1 中,較之于算法1 ~4,算法2.1 有更好的收斂效果.能否進一步削弱變分不等式的條件及探索算法2.1 的更多應用,是將來進一步的工作.

