帶磁場項的非線性Schr?dinger 方程解的有限時間爆破
帥 鯤, 潘志剛, 蒲志林, 熊 胤
(1.電子科技大學(xué) 成都學(xué)院,四川 成都611731; 2.西南交通大學(xué) 數(shù)學(xué)學(xué)院,四川 成都610031;3.四川師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院,四川 成都610066; 4.四川師范大學(xué) 法學(xué)院,四川 成都610066)
本文考慮如下帶磁場項的非線性Schr?dinger方程:
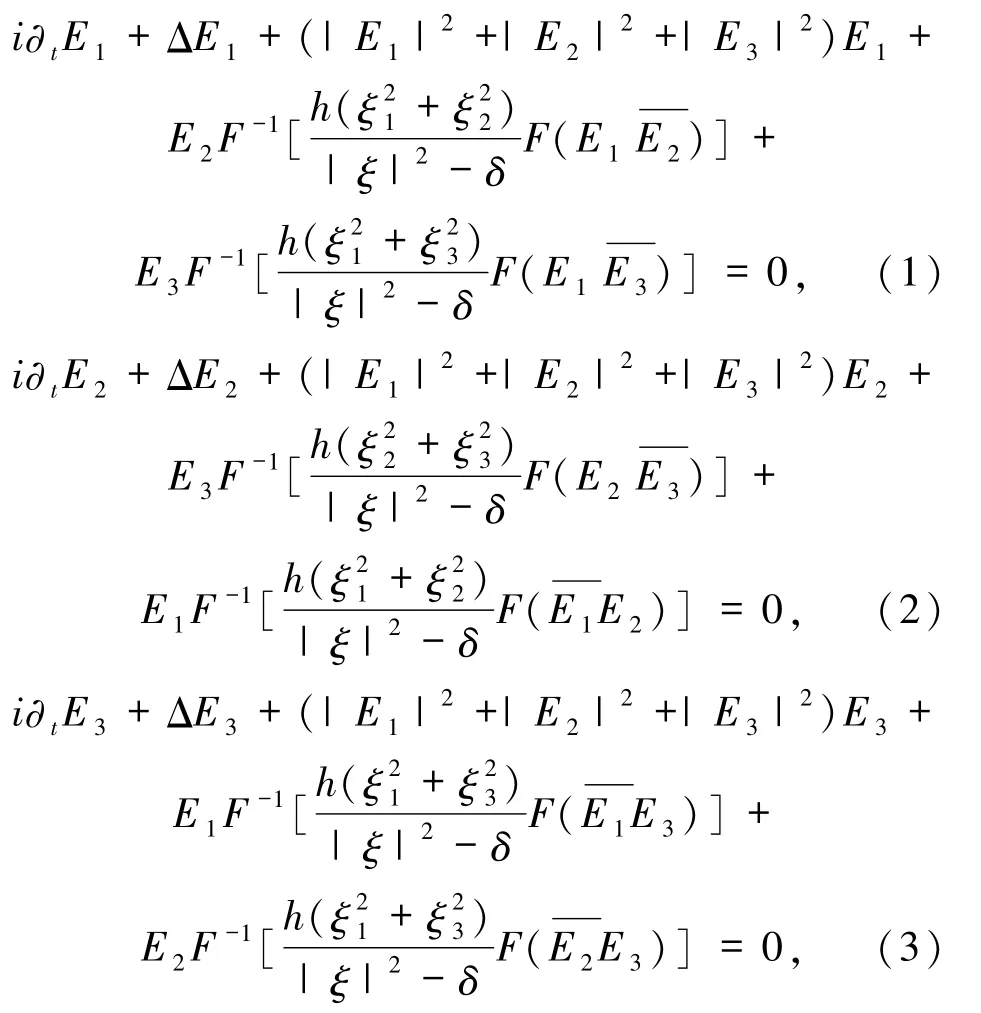
其初值滿足:
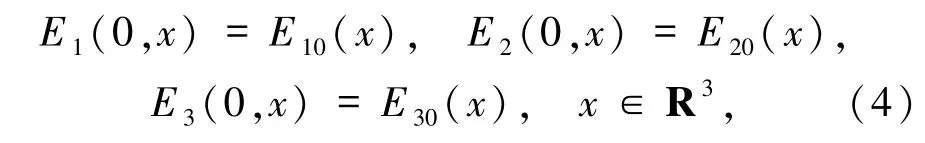
其中,E(t,x)為R+×R3到C3的矢量函數(shù),常數(shù)δ≤0,h >0.方程(1)~(3)也稱為帶奇異積分算子的非線性Schr?dinger方程.
若不考慮磁場項的影響,方程(1)~(3)簡化為
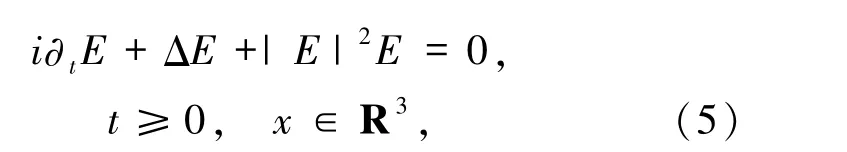
其中E =(E1,E2,E3).該方程為量子力學(xué)中的經(jīng)典模型.目前,關(guān)于不帶磁場項的Schr?dinger 方程的解爆破性質(zhì)的研究已經(jīng)比較成熟[1-2].然而,對帶磁場項的Schr?dinger 方程(1)~(3),盡管物理學(xué)上已經(jīng)表明了解在有限時間爆破[3-4],據(jù)我們所知還沒有方程(1)~(3)奇異解存在的結(jié)果.
基于文獻(xiàn)[5 -8]的方法,克服非線性奇異積分算子的困難,得到了方程(1)~(4)柯西問題在有限時間爆破的初值條件.
1 預(yù)備知識
令wi>0,Ei(t,x)=eiwitui(x),i =1,2,3,(u1(x),u2(x),u3(x))為以下靜態(tài)問題的解:
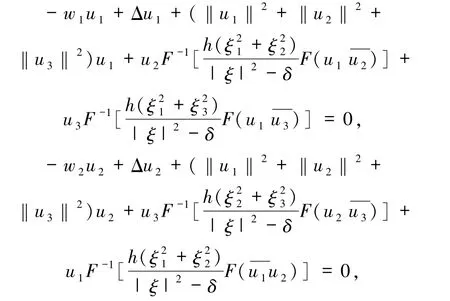
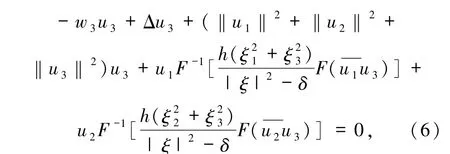
其中(u1,u2,u3)∈H1(R3)×H1(R3)×H1(R3),(u1,u2,u3)≠(0,0,0).定義以下泛函:
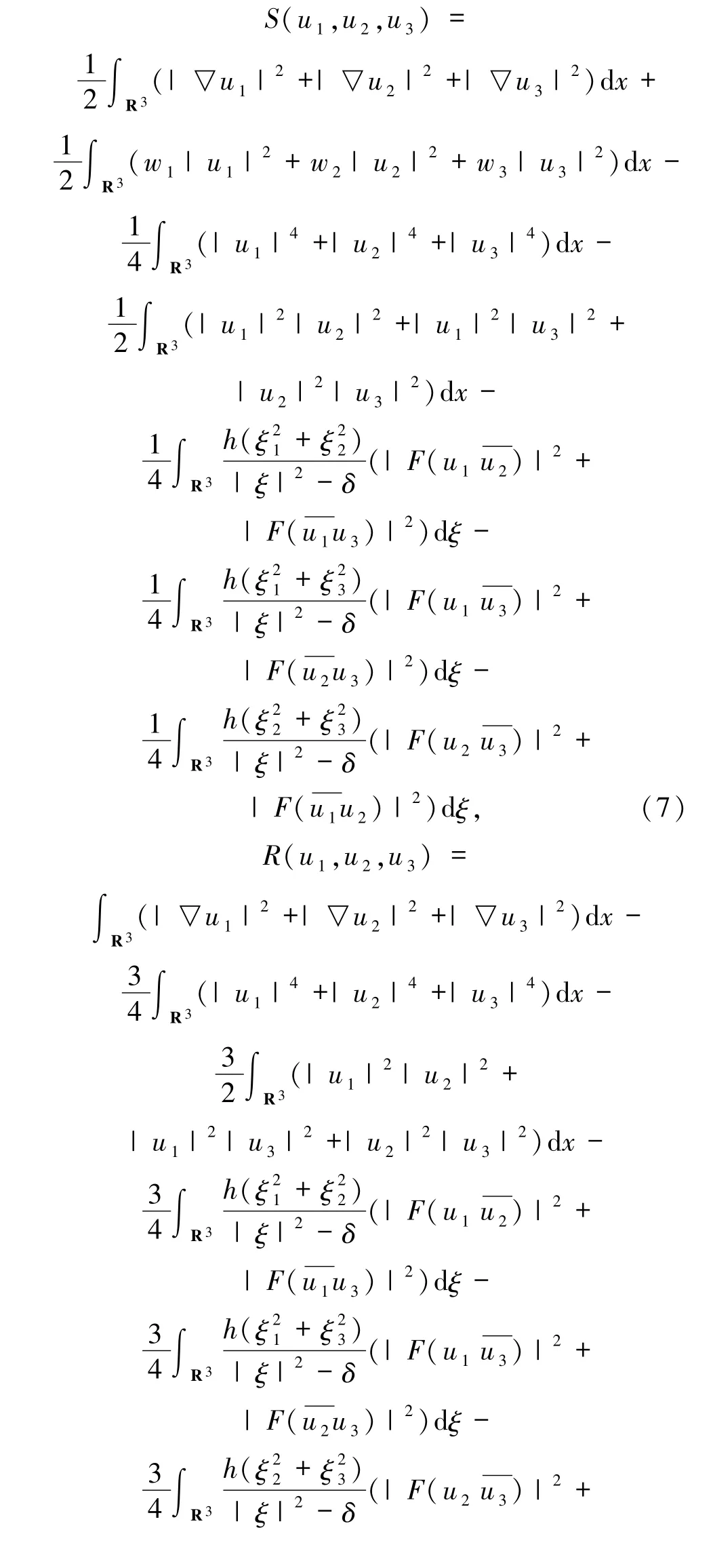

由Sobolev 嵌入定理和傅里葉變換,知S(u1,u2,u3)和R(u1,u2,u3)都是適定的.
此外,定義集合M為
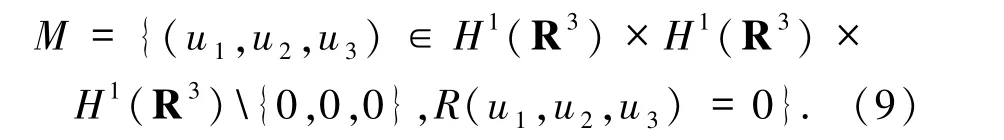
強(qiáng)制變分問題為
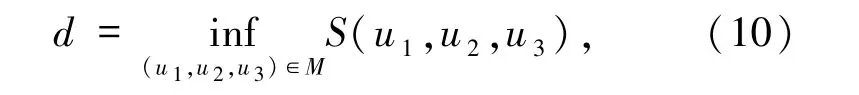
參見文獻(xiàn)[9],知道存在(Q,P,V)∈H1(R3)×H1(R3)×H1(R3)\{(0,0,0)}滿足
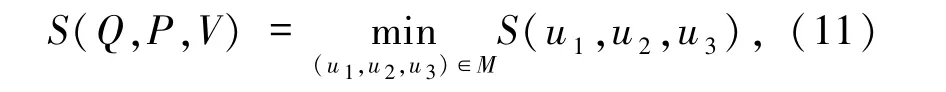
而以下結(jié)論成立.
引理1.1 由(11)式,則R(Q,P,V)=0 且
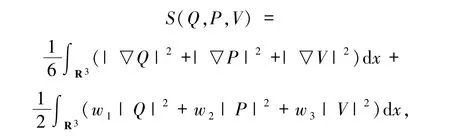
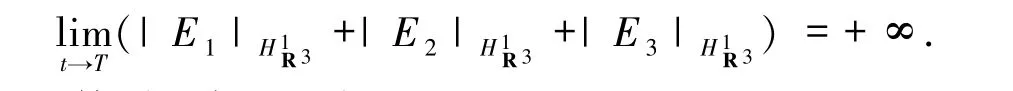
此外,得到以下引理.
引理1.2 令(E1,E2,E3)為柯西問題(1)~(4)的光滑解,則總質(zhì)量和能量守恒
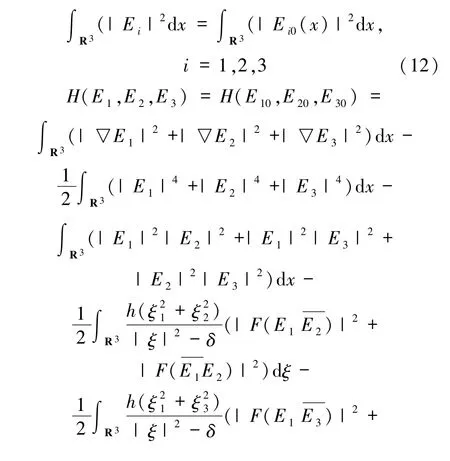
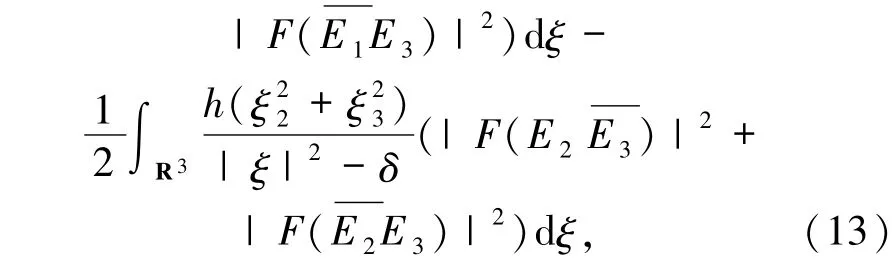
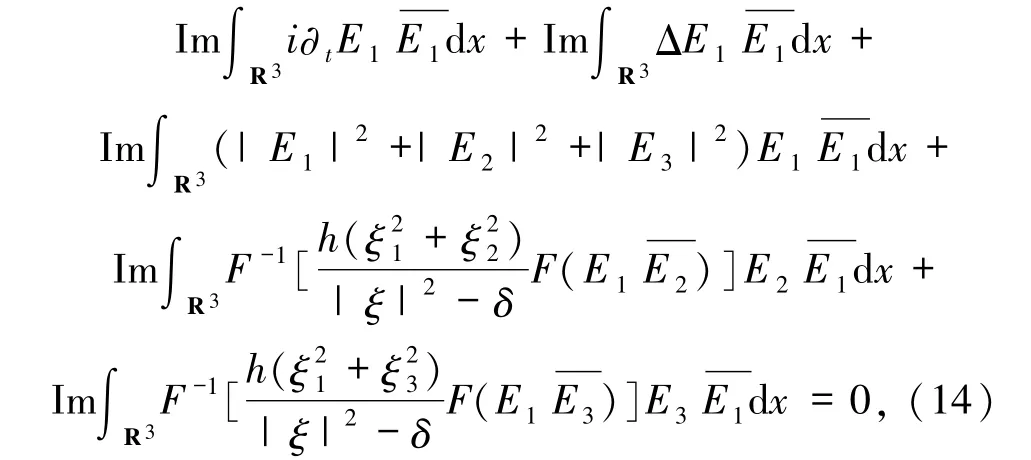
通過積分運算,則有
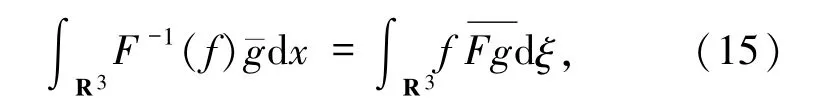
得到
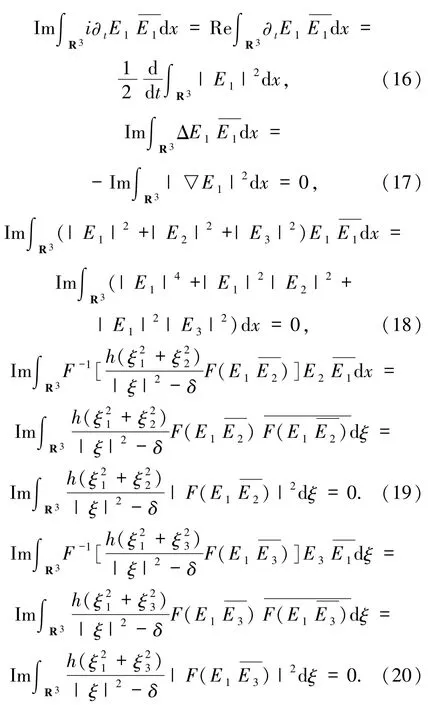
把(15)~(18)式代入(14)式,得到
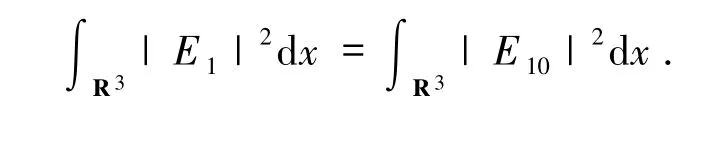
同理可得
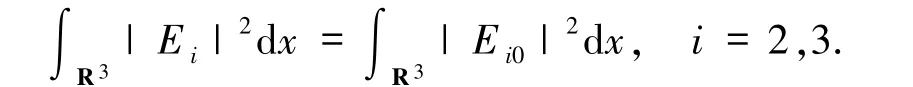
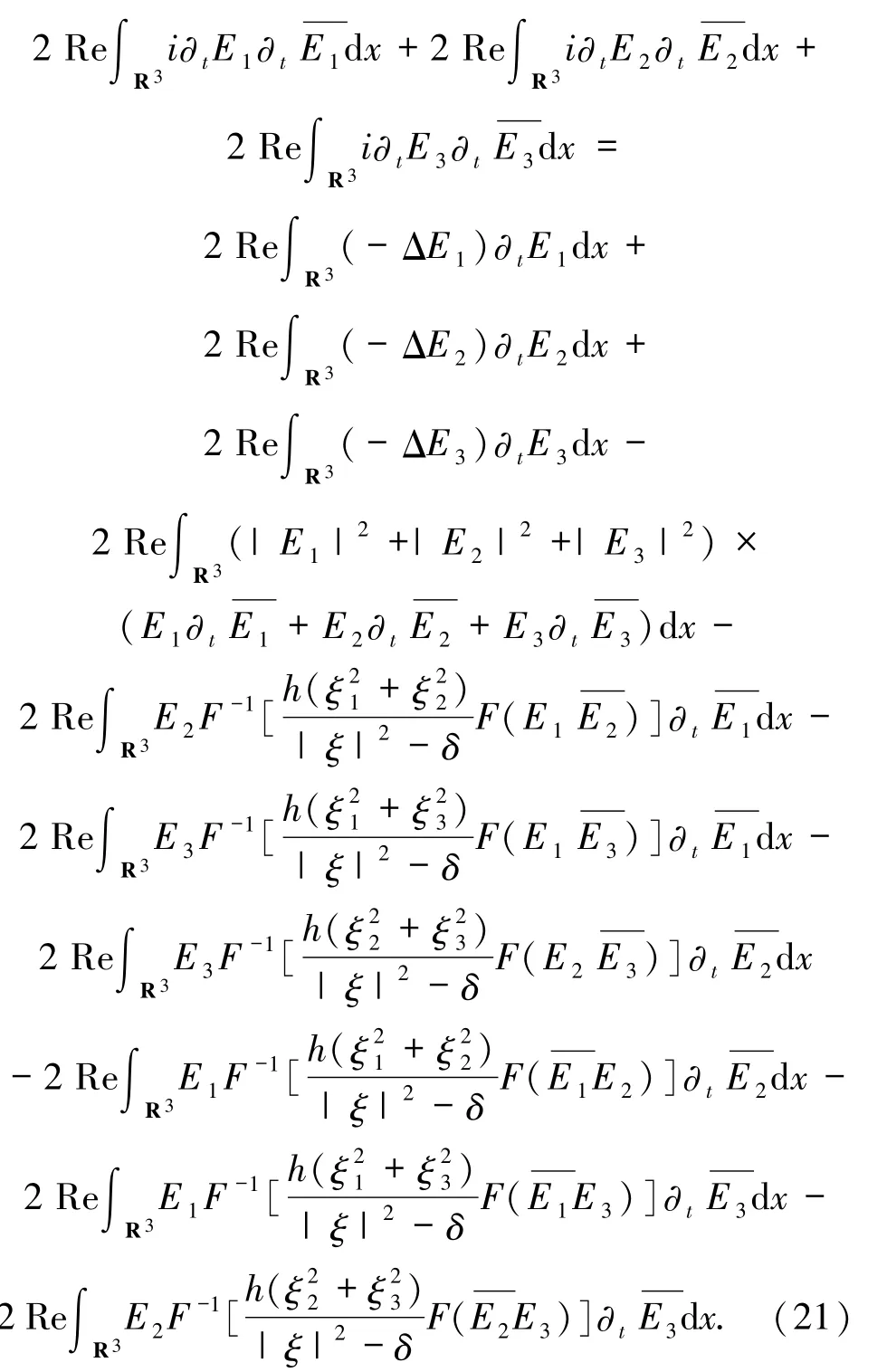
積分運算可得:
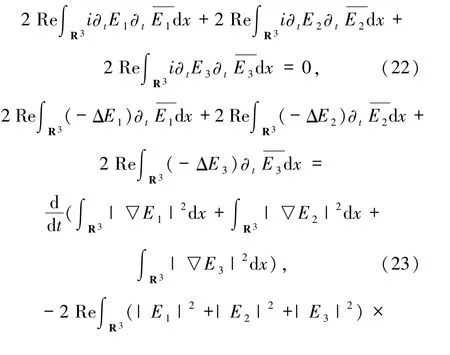

通過對(25)式積分運算,得到
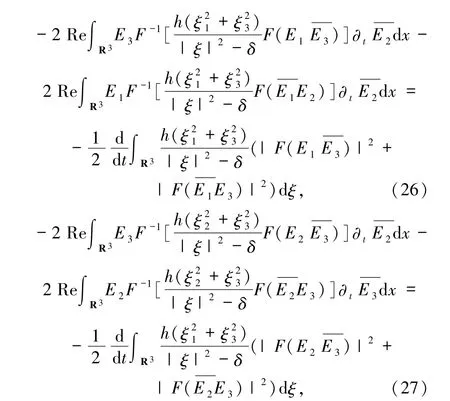
把(22)~(27)式代入(21)式,得到
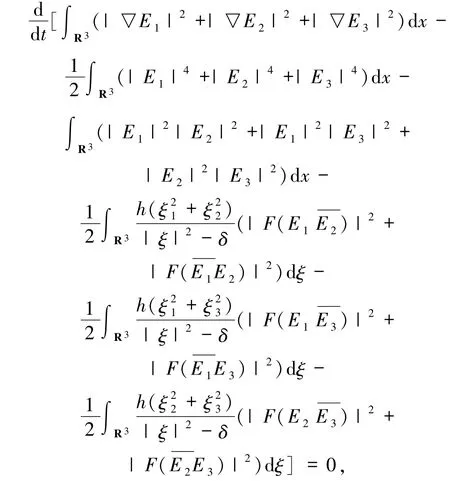
因此(13)式成立.
2 主要結(jié)果
令
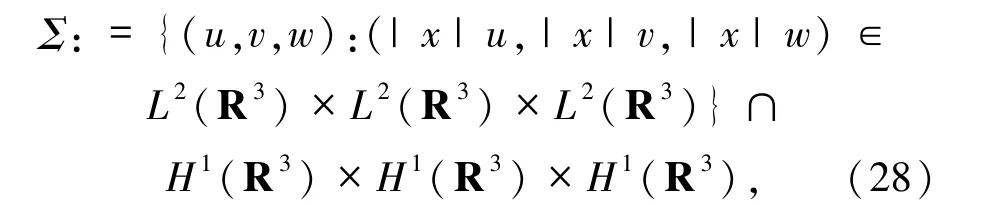
命題2.1 令(E10,E20,E30)∈Σ 且(E1,E2,E3)∈C([0,T];Σ)為柯西問題(1)~(4)在[0,T)上的解.記
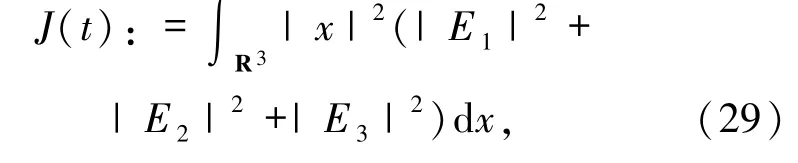
則
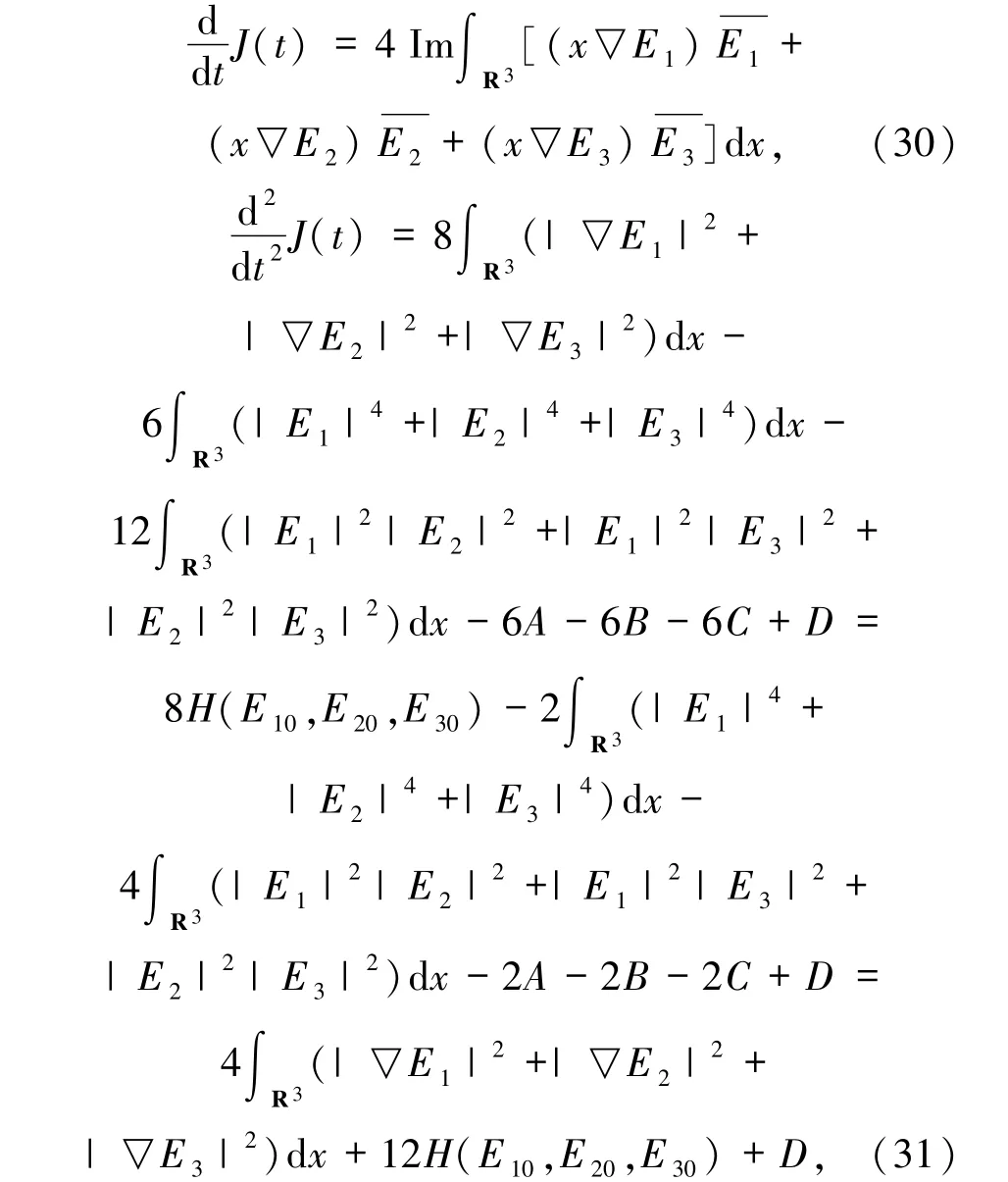
其中
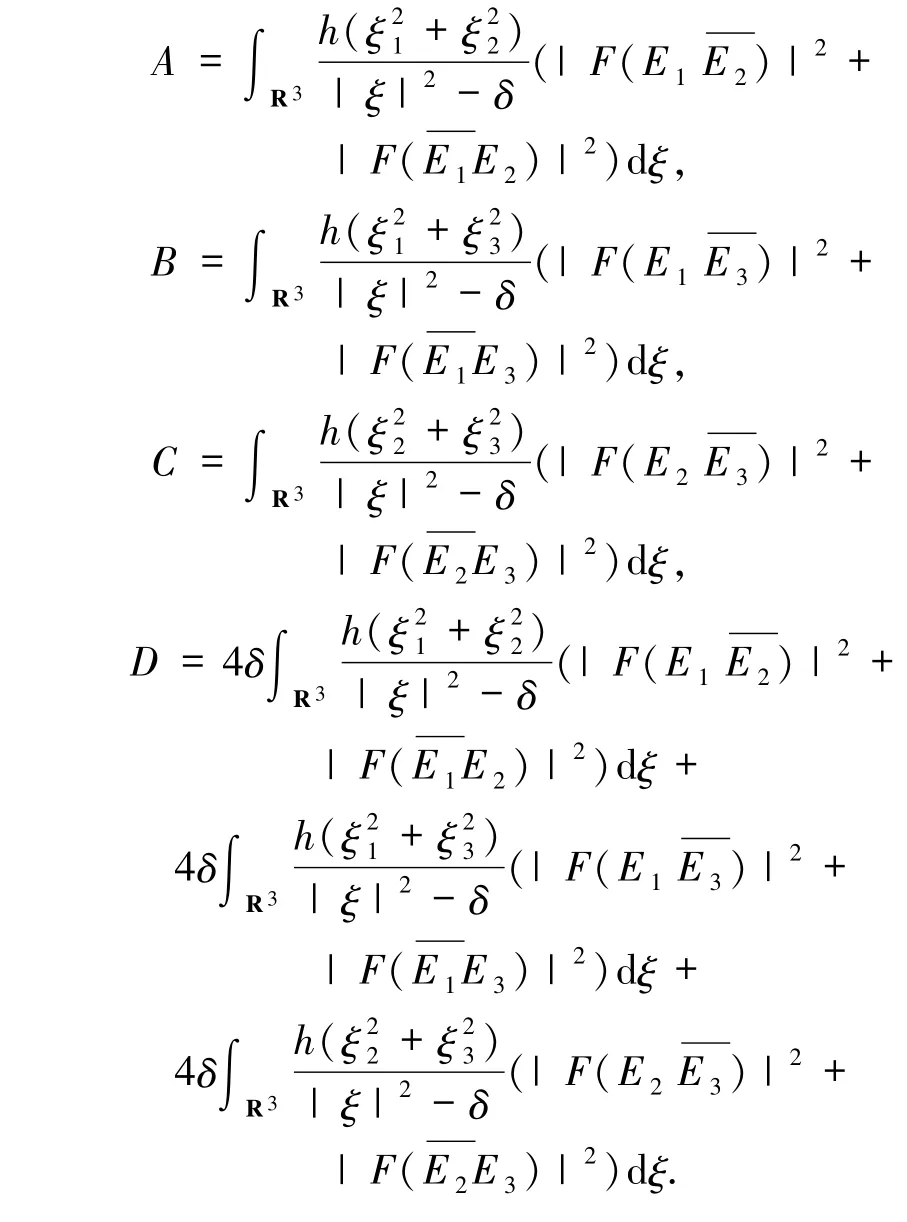
證明 因為(E1,E2,E3)∈C([0,T];Σ)是柯西問題(1)~(4)式在[0,T)上的解.由(E10,E20,E30)∈Σ 和文獻(xiàn)[14],有(E1,E2,E3)∈Σ.由(1)~(3)和(29)式可得
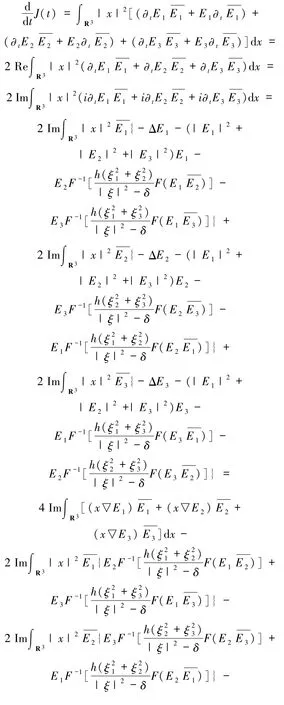
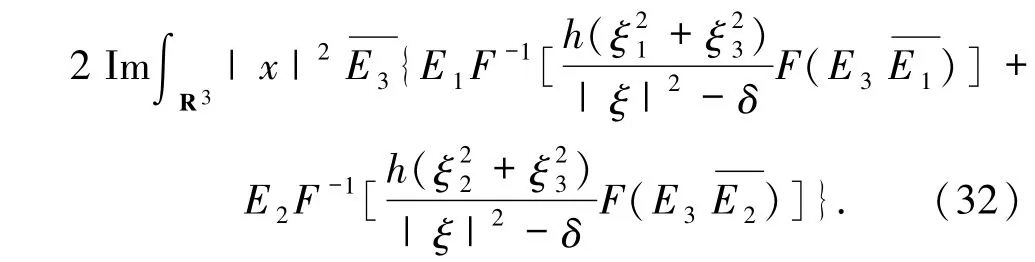
又因為
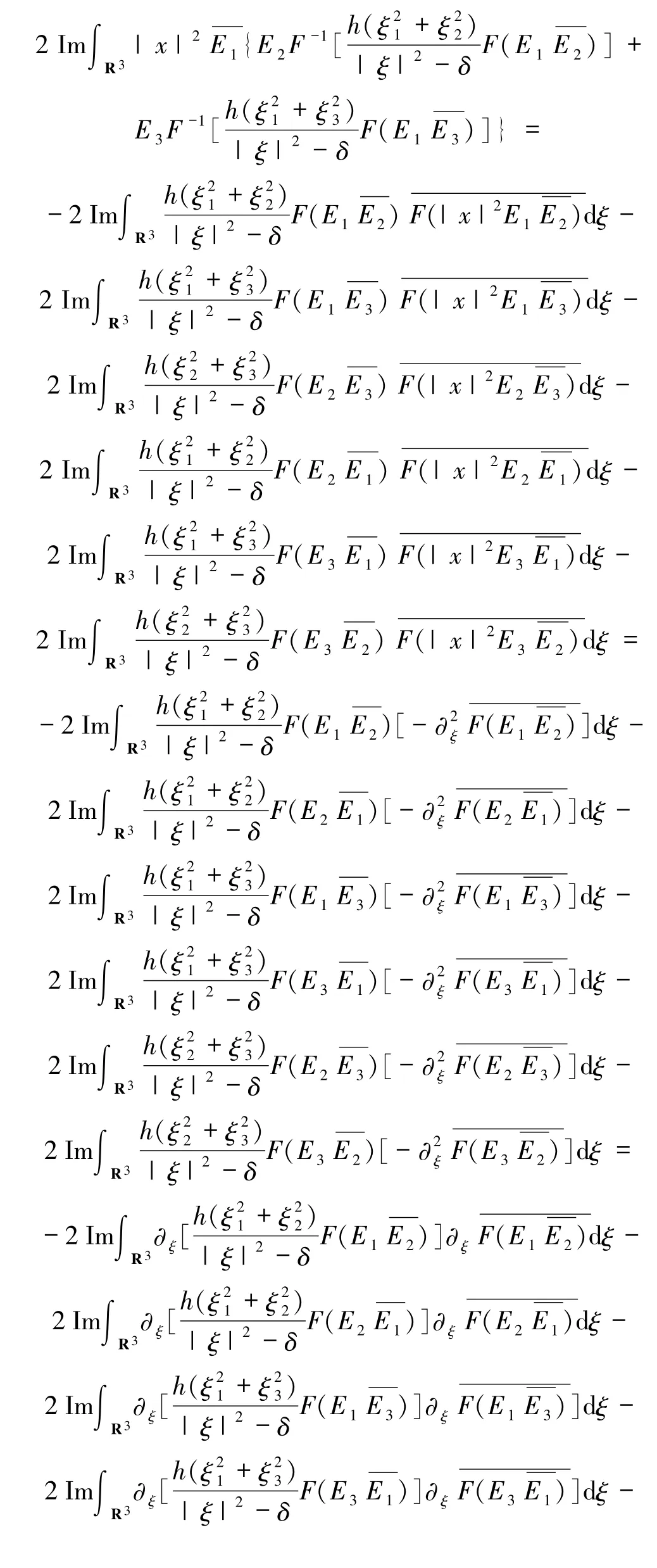

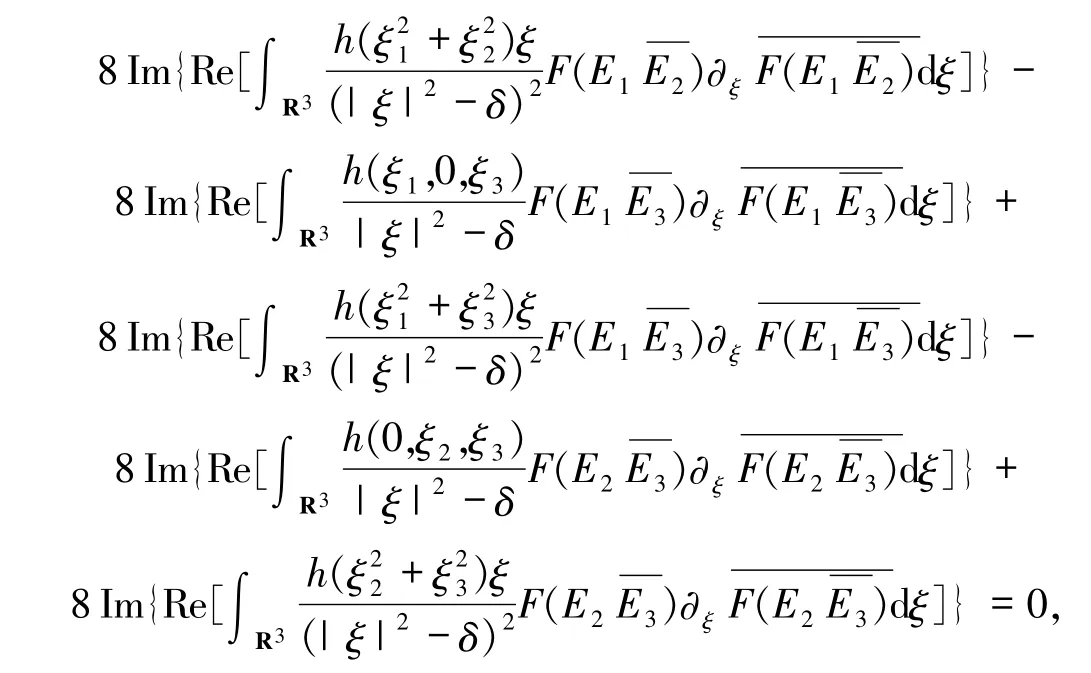
根據(jù)(32)式可得
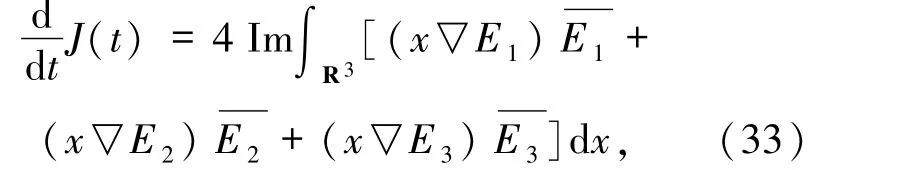
在(33)式中關(guān)于t求導(dǎo),運用(1)~(3)式得到+
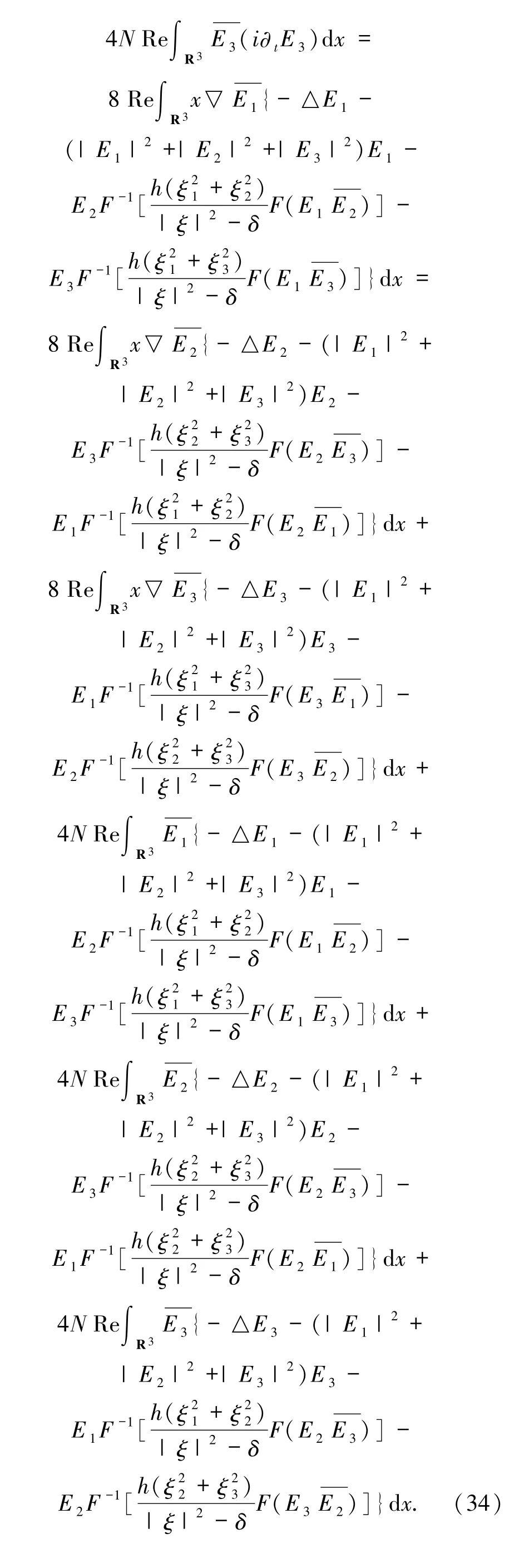
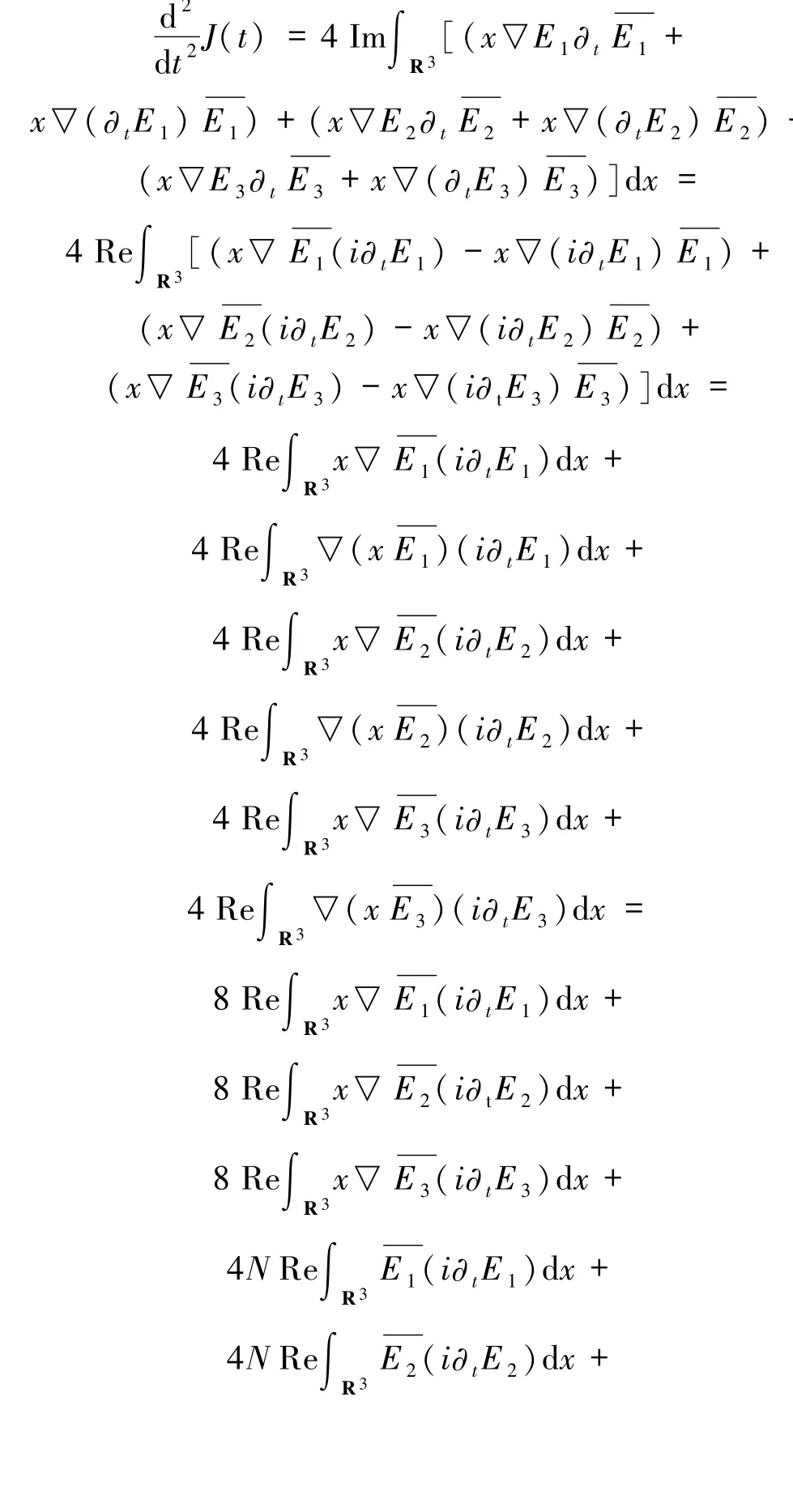
由(34)式積分可得:
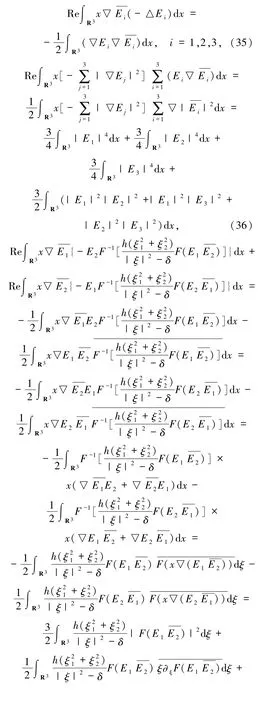
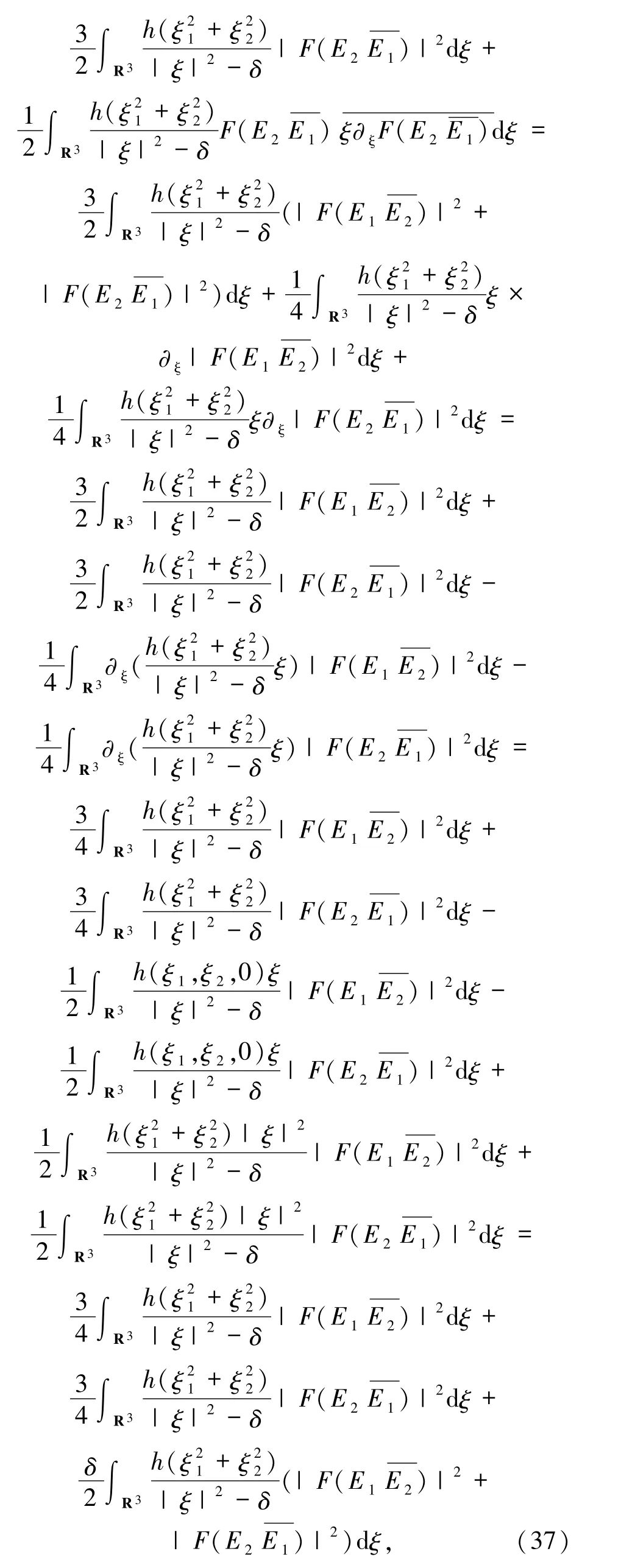
同理,(37)式通過積分運算得到
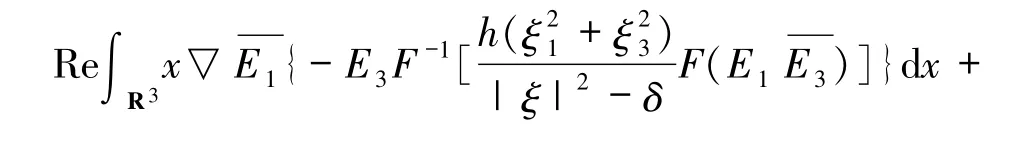
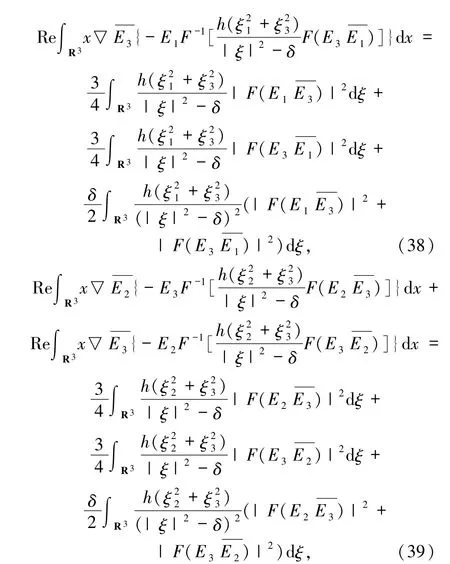
此外有
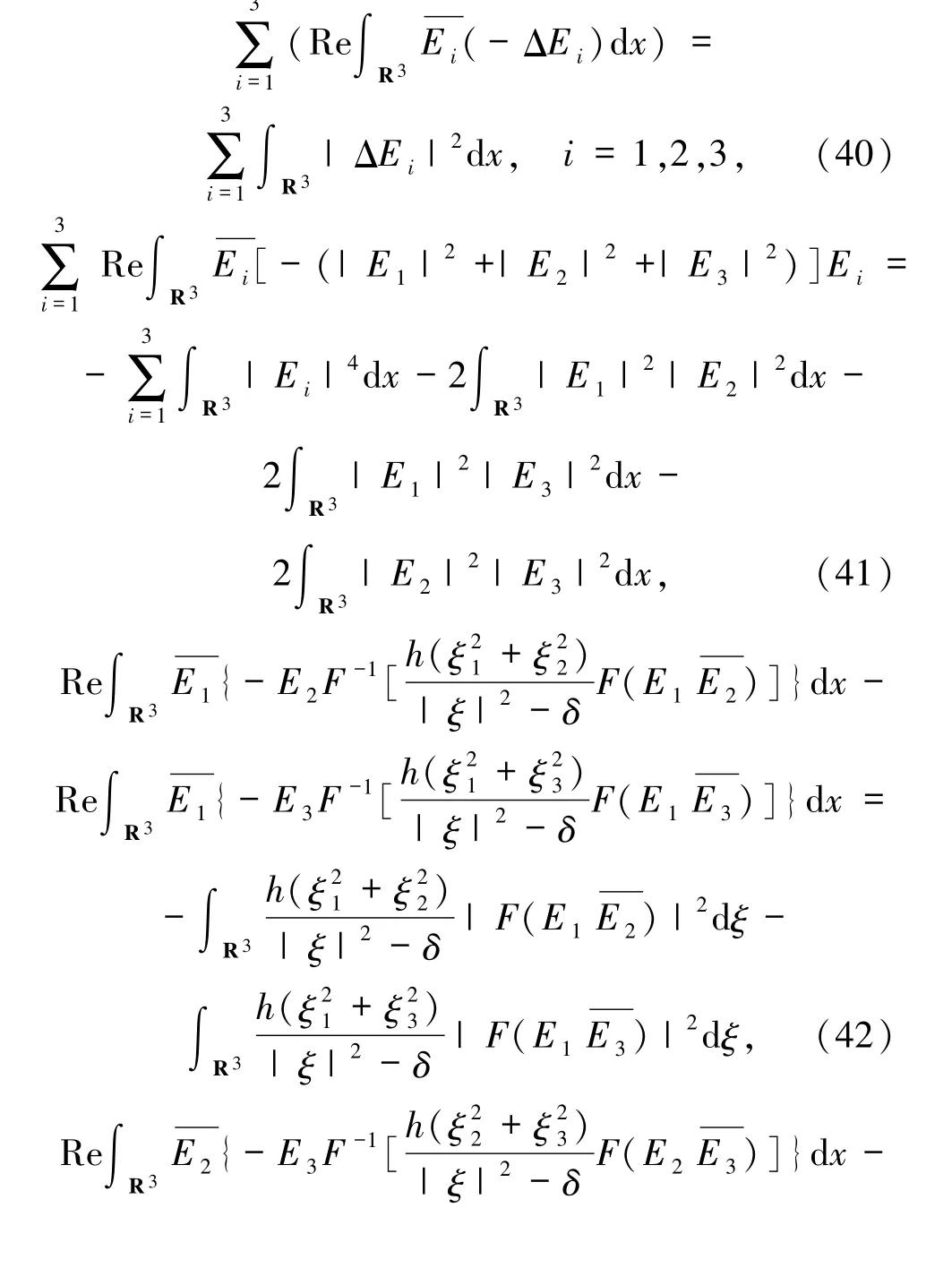
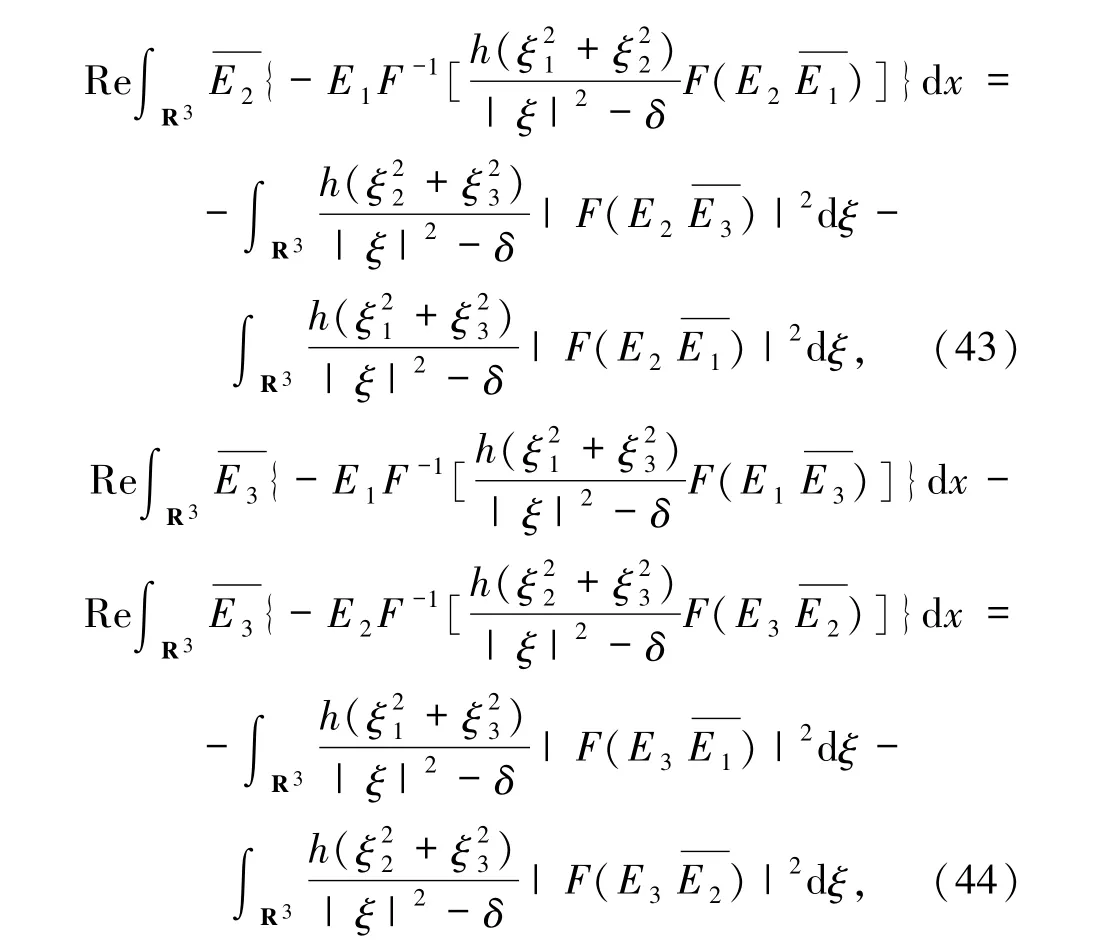
把(35)~(44)式代入(34)式可得
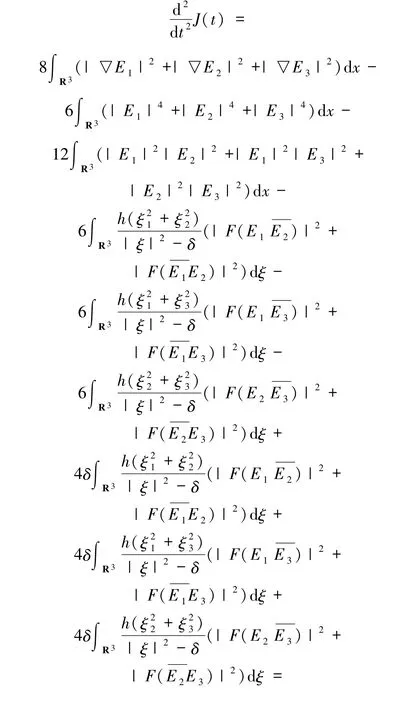
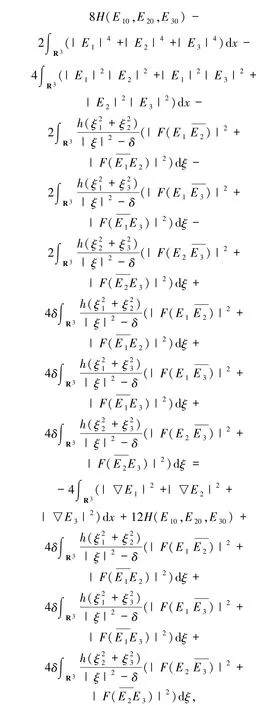
至此,命題2.1 的證明完畢.
參見文獻(xiàn)[15]有如下引理.
引理2.1 令f是標(biāo)量函數(shù),如果|x |f和▽f在L2(RN)中,則f在L2(RN)中并且滿足
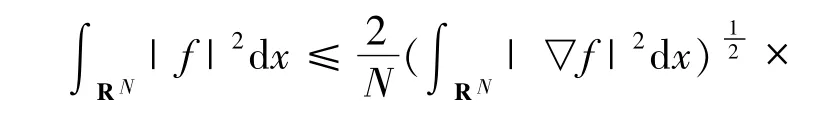
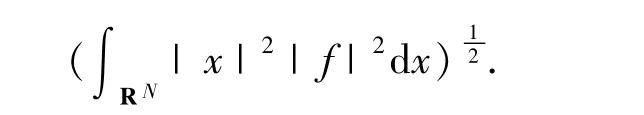
定理2.1 設(shè)(E1,E2,E3)為方程(1)~(4)的一類徑向?qū)ΨQ解且(E10,E20,E30)∈S,若
(i)H(E10,E20,E30)≤0;
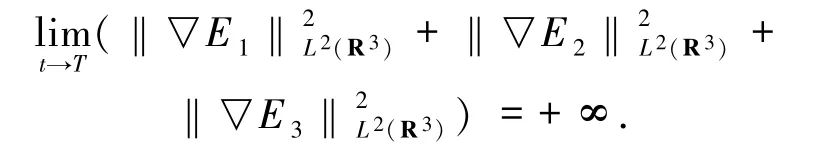
證明 令
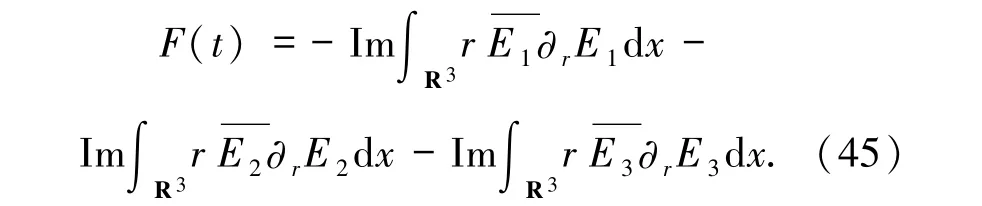
由(ii)可得F(0)>0.此外,由命題2.1 有
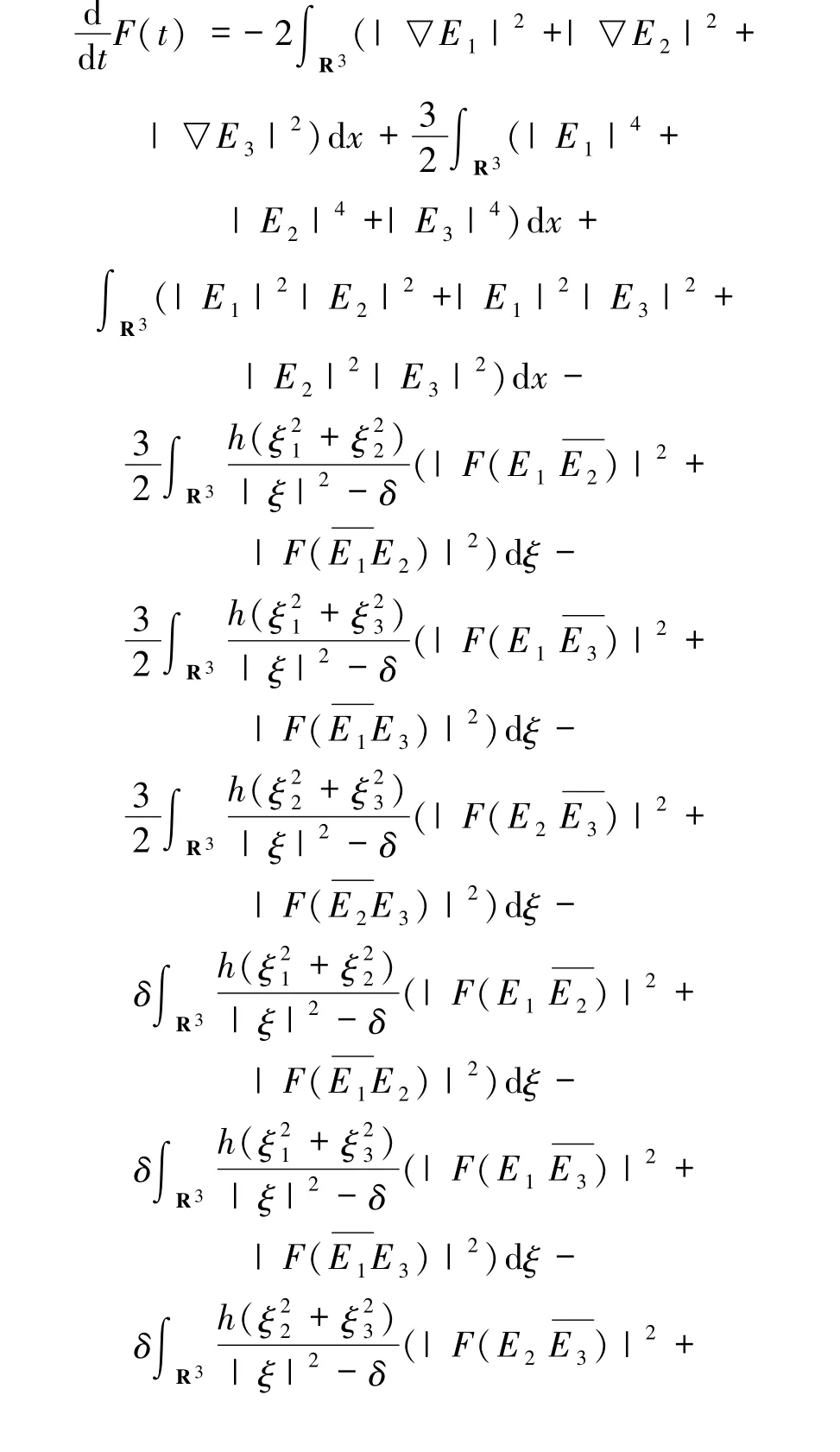
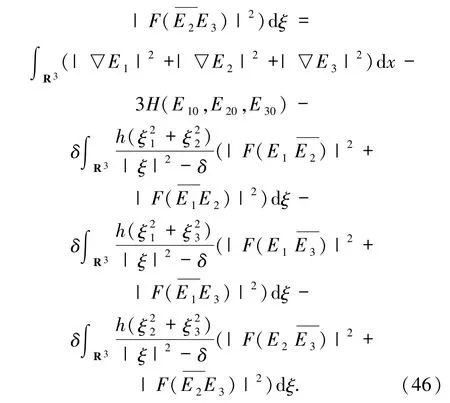
由于h >0 且δ≤0,(i)蘊含了
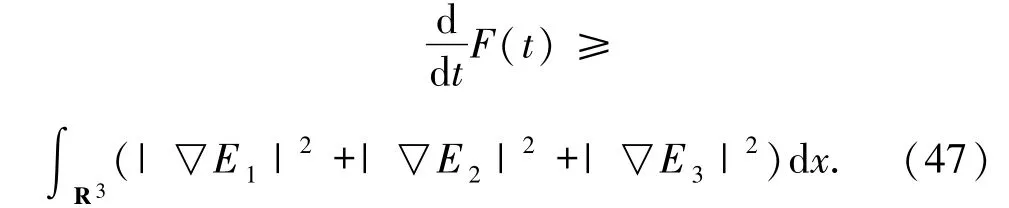
由F(0)>0 和(47)式,可得F(t)>0,由(E1,E2,E3)存在性和(30)式有
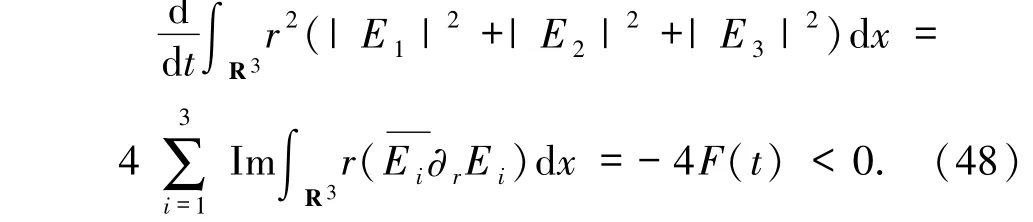
因此,
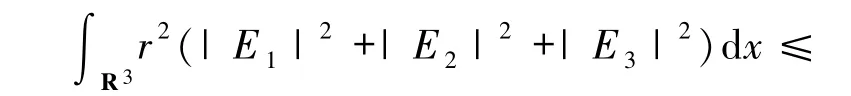
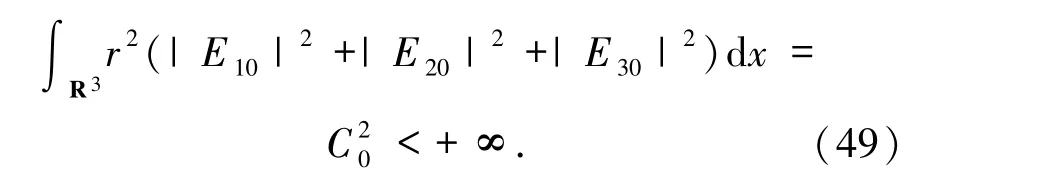
運用Schwarz不等式可得
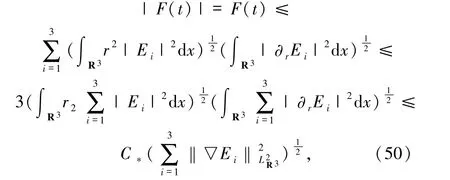
其中C*≥3C0.因此,由(47)和(50)式蘊含了
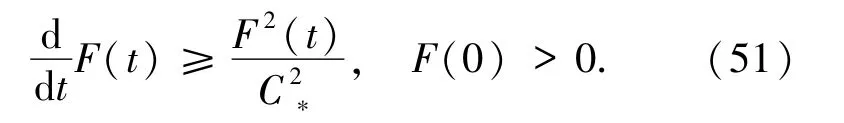
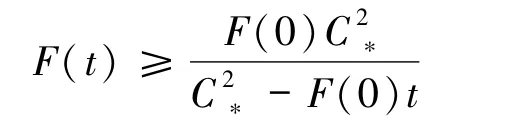
成立,從而
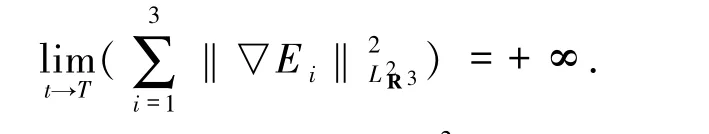
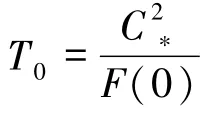
致謝 天津大學(xué)數(shù)學(xué)系的甘在會教授在論文寫作過程中給予的指導(dǎo)與寶貴建議,謹(jǐn)致謝意.

