不確定性環(huán)境下可再生能源系統(tǒng)新優(yōu)化模型*

陽彩霞，萬 中

(1.華南理工大學(xué)廣州學(xué)院，計(jì)算機(jī)工程學(xué)院，廣東廣州 510800；2.中南大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，湖南長(zhǎng)沙 410083)

0 引言

近年來，隨著能源的減少和人類環(huán)保意識(shí)的增強(qiáng)，可再生能源得到了愈來愈多的關(guān)注。合理開發(fā)利用可再生能源對(duì)解決全世界的能源與環(huán)境危機(jī)有著舉足輕重的作用。國(guó)內(nèi)外很多學(xué)者為緩解能源消費(fèi)與環(huán)境保護(hù)之間的矛盾，研究了可再生能源管理系統(tǒng)的各種規(guī)劃模型[1-9]。Cai 等[7]結(jié)合兩階段區(qū)間規(guī)劃和機(jī)會(huì)約束規(guī)劃研究了不確定環(huán)境下多地區(qū)、多時(shí)期、多品種、多部門之間的可再生能源綜合規(guī)劃問題，建立了以系統(tǒng)成本最小為目標(biāo)的優(yōu)化模型。萬中等[8]研究了不確定環(huán)境下長(zhǎng)株潭城市群的可再生能源管理系統(tǒng)并建立規(guī)劃模型，但沒有進(jìn)行算例驗(yàn)證。在Cai等[7]和萬中等[8]的基礎(chǔ)上，陽彩霞[9]結(jié)合區(qū)間線性規(guī)劃、混合整數(shù)規(guī)劃和新提出的滿意度方法，建立了不確定環(huán)境下可再生能源管理系統(tǒng)的兩階段規(guī)劃子模型，并以最好最優(yōu)解和最差最優(yōu)解組成最優(yōu)解區(qū)間，但不能保證最好最優(yōu)解一定比最差最優(yōu)解好(即區(qū)間的左端點(diǎn)比右端點(diǎn)小)。為解決這個(gè)難題，本文針對(duì)陽彩霞[9]所研究的模型背景，結(jié)合滿意度方法、0-1整數(shù)規(guī)劃和徐澤水等[10]提出的可能度方法，建立多態(tài)不確定環(huán)境下可再生能源系統(tǒng)的新優(yōu)化模型,通過模型給出能源配置方案的確定性最優(yōu)解，從而避免了可再生能源系統(tǒng)模型可能無解的狀況。

1 處理隨機(jī)不等式的滿意度方法

x≤y的滿意度，記為λ(x≤y)。

這里，x和y不能同時(shí)取常數(shù)。易得滿意度λ(x≤y)∈(-,+)。

設(shè)有隨機(jī)向量A=(α1,α2,…,αn)，隨機(jī)變量b和決策向量X=(x1,x2,…,xn)T，決策者對(duì)隨機(jī)不等式

AX≤b，

(1)

的滿意度水平為λ0，根據(jù)定義有

(2)

即在滿意度λ0下，隨機(jī)不等式(1)可轉(zhuǎn)化為其確定性等價(jià)類(2)式，該轉(zhuǎn)化方法稱為滿意度方法。它只涉及隨機(jī)參數(shù)的期望和方差，不需要考慮其具體分布類型。

2 可再生能源系統(tǒng)的新優(yōu)化模型

假設(shè)需要制定3個(gè)地區(qū)的長(zhǎng)期(分為3個(gè)規(guī)劃期)能源規(guī)劃方案。為方便研究，將終端消費(fèi)分為4個(gè)部門：①農(nóng)業(yè)(包括農(nóng)、林、牧、漁業(yè))；②商業(yè)(包括批發(fā)、零售業(yè)，住宿、餐飲業(yè)，生活消費(fèi)和其他)；③工業(yè)(包括工業(yè)和建筑業(yè))；④交通系統(tǒng)(包括交通運(yùn)輸、倉(cāng)儲(chǔ)和郵政業(yè))。3個(gè)地區(qū)都有柴油、汽油、天然氣、煤炭4種常規(guī)能源和水能、太陽能、風(fēng)能3種可再生能源。柴油、汽油用于交通系統(tǒng)和儲(chǔ)備發(fā)電。天然氣用于工業(yè)、商業(yè)供熱。煤炭用于火力發(fā)電和工業(yè)、商業(yè)需求。3種可再生能源用于發(fā)電，且每個(gè)地區(qū)都有相應(yīng)的發(fā)電設(shè)備(有容量限制)和技術(shù)。若電力需求量在容量限制范圍內(nèi)，則可再生能源發(fā)電只存在發(fā)電成本；若電力需求量超出容量限制，則可再生能源發(fā)電設(shè)備在3個(gè)規(guī)劃期內(nèi)可以增容一次，但會(huì)產(chǎn)生額外的增容成本。

由于可再生資源的可利用量不穩(wěn)定，因此不適合用確定數(shù)表示，但它具有明顯的概率分布特征。例如，太陽能可利用量一般近似服從正態(tài)分布，風(fēng)能可利用量一般服從威爾布分布[7]。而能源價(jià)格、需求量、發(fā)電轉(zhuǎn)化率等參數(shù)往往也是不確定的，雖然較難獲取其概率分布信息，但容易得到其可能取值范圍，因此適合用區(qū)間數(shù)[a-,a+]來表示。

分別用滿意度方法和可能度方法處理約束條件中的隨機(jī)不等式[9]和區(qū)間不等式[10]，可得到多態(tài)不確定環(huán)境下可再生能源系統(tǒng)的新優(yōu)化模型，其目標(biāo)函數(shù)為最小化能源系統(tǒng)總成本，分為下述3個(gè)部分。

①柴油、汽油、天然氣和煤炭的供應(yīng)成本

②水力、太陽能、風(fēng)力、柴油、汽油和煤炭的發(fā)電成本

③水力、太陽能、風(fēng)力發(fā)電的增容成本

記不同區(qū)間不等式的可能度水平為βi(i=1,…,13)，不同區(qū)間不等式的滿意度水平為λi(i=1,2)，約束條件可分為

①柴油、汽油、天然氣和煤炭的供需平衡

(3)

(4)

(5)

(6)

②水能、太陽能、風(fēng)能的可利用量限制

(7)

(8)

(9)

③電力供需平衡

(10)

④水力、太陽能、風(fēng)力發(fā)電設(shè)備的裝機(jī)容量限制

(11)

(12)

(13)

⑤柴油和汽油儲(chǔ)備發(fā)電設(shè)備裝機(jī)容量限制

(14)

(15)

⑥3類決策變量限制

上述各式中，決策變量X1,t,X2,t,X3,t,X4,t分別表示t時(shí)期的柴油、汽油、天然氣和煤炭供應(yīng)量(單位：TJ)；Y1,m,t,Y2,m,t,Y3,m,t,Y4,m,t,Y5,m,t,Y6,m,t分別表示t時(shí)期m地區(qū)水力、太陽能、風(fēng)力、柴油、汽油和煤炭的發(fā)電量(單位：MW)；Z1,n,Z2,n,Z3,n分別表示第n選項(xiàng)下水力、太陽能、風(fēng)力發(fā)電的增容選擇，取0表示不增容，取1表示增容；參數(shù)VHm,t,VSm,t,VWm,t,VDm,t,VGm,t,VCm,t分別表示t時(shí)期m地區(qū)水力、太陽能、風(fēng)力、儲(chǔ)備柴油、汽油和煤炭的平均發(fā)電成本(單位：$103/MW)；IHn,ISn,IWn分別表示水力、太陽能、風(fēng)力發(fā)電的平均增容成本(單位：$103/MW)；EHn,ESn,EWn分別表示第n選項(xiàng)下水力、太陽能、風(fēng)力發(fā)電的增容量(單位：MW)；DTDm,t,DTGm,t,DINm,t,DMNm,t,DICm,t,DMCm,t,DIEm,t,DMEm,t,DAEm,t分別表示t時(shí)期m地區(qū)交通柴油、交通汽油、工業(yè)天然氣、商業(yè)天然氣、工業(yè)煤炭、商業(yè)煤炭、工業(yè)電力、商業(yè)電力和農(nóng)業(yè)電力的需求量(單位：TJ)；FEDm,t,FEGm,t,FECm,t,FEHm,t,FESm,t,FEWm,t分別表示t時(shí)期m地區(qū)的柴油、汽油、煤炭、水力、太陽能和風(fēng)力的發(fā)電轉(zhuǎn)換率；RCH,RCS,RCW分別表示水力、太陽能和風(fēng)力發(fā)電廠的現(xiàn)有裝機(jī)容量(單位：MW)；AVHt,AVSt,AVWt分別表示t時(shí)期水力、太陽能和風(fēng)力的可利用量(單位：MW)；UP4,m,t,UP5,m,t分別表示t時(shí)期m地區(qū)用于儲(chǔ)備發(fā)電的柴油量和汽油量上限 (單位：MW)；UCAP表示發(fā)電廠的能量轉(zhuǎn)換系數(shù)。

3 算例分析

3.1 最優(yōu)值和最優(yōu)解

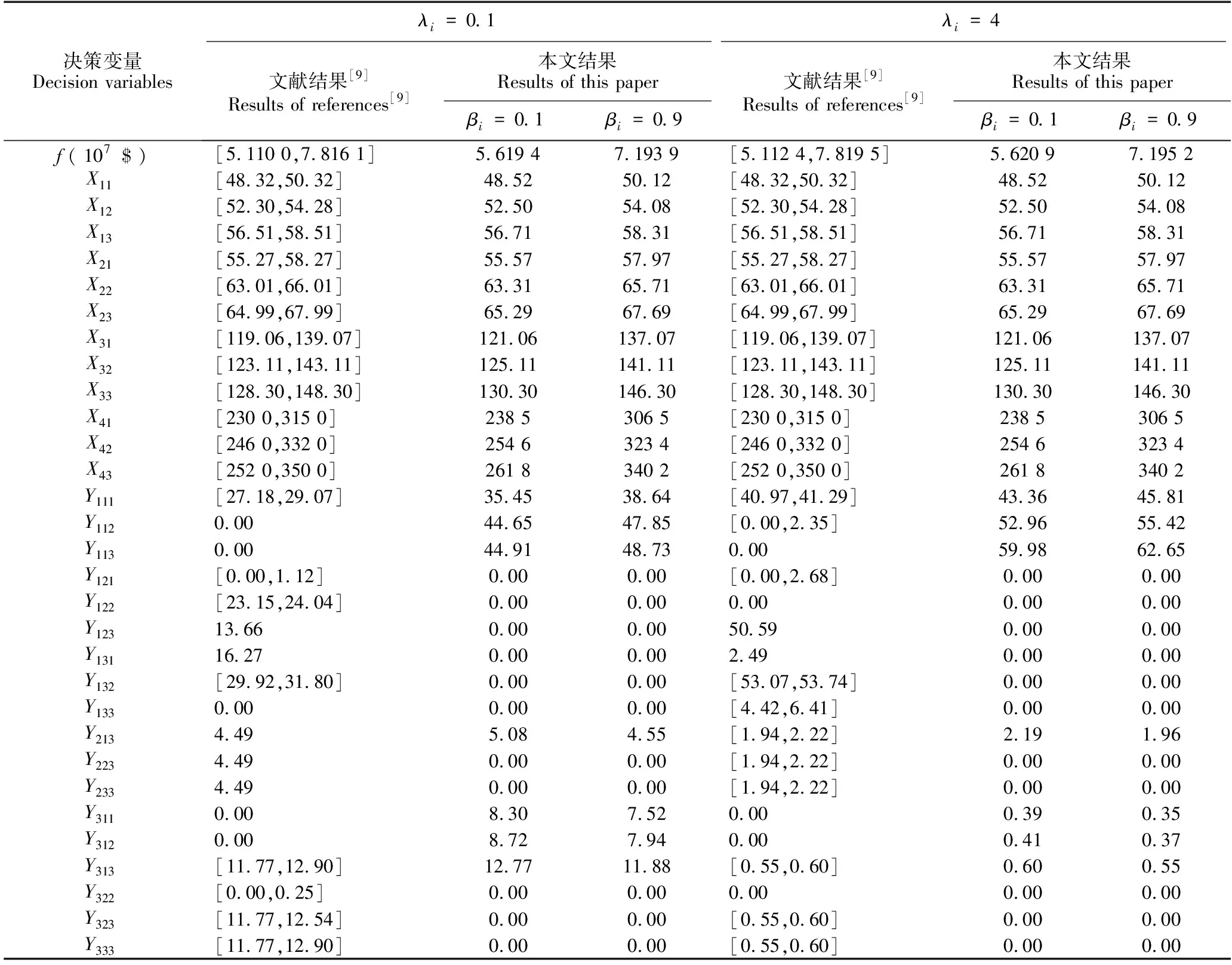
為了更好地進(jìn)行比較分析，本文模型中的所有參數(shù)全部沿用文獻(xiàn)[9]的數(shù)據(jù)。若目標(biāo)函數(shù)中取折中系數(shù)0.5，使用Lingo軟件編程可求得新模型在不同可能度和滿意度水平下的最優(yōu)值和最優(yōu)解。具體結(jié)果見表1，未列出決策變量的取值全為0。

3.2 結(jié)果與分析

(1)與文獻(xiàn)[9]的數(shù)值結(jié)果相比，本文模型的最優(yōu)值(系統(tǒng)總成本)和4種常規(guī)能源的供應(yīng)量Xi,t(i=1,2,3,4)完全在文獻(xiàn)[9]所得結(jié)果對(duì)應(yīng)區(qū)間內(nèi)，但Yj,m,t(j=1,2,3)的取值反映了3種可再生能源的配置方案有很大不同，可見帶有不確定性的可再生能源在系統(tǒng)中的敏感度很高。

表1 數(shù)值結(jié)果

Table 1 Numerical results

決策變量Decision variablesλi=0.1λi=4文獻(xiàn)結(jié)果[9]Results of references[9] 本文結(jié)果Results of this paperβi=0.1βi=0.9文獻(xiàn)結(jié)果[9]Results of references[9]本文結(jié)果Results of this paperβi=0.1βi=0.9f(107$)[5.110 0,7.816 1]5.619 47.193 9[5.112 4,7.819 5]5.620 97.195 2X11[48.32,50.32]48.5250.12[48.32,50.32]48.5250.12X12[52.30,54.28]52.5054.08[52.30,54.28]52.5054.08X13[56.51,58.51]56.7158.31[56.51,58.51]56.7158.31X21[55.27,58.27]55.5757.97[55.27,58.27]55.5757.97X22[63.01,66.01]63.3165.71[63.01,66.01]63.3165.71X23[64.99,67.99]65.2967.69[64.99,67.99]65.2967.69X31[119.06,139.07]121.06137.07[119.06,139.07]121.06137.07X32[123.11,143.11]125.11141.11[123.11,143.11]125.11141.11X33[128.30,148.30]130.30146.30[128.30,148.30]130.30146.30X41[230 0,315 0]238 5306 5[230 0,315 0]238 5306 5X42[246 0,332 0]254 6323 4[246 0,332 0]254 6323 4X43[252 0,350 0]261 8340 2[252 0,350 0]261 8340 2Y111[27.18,29.07]35.4538.64[40.97,41.29]43.3645.81Y1120.0044.6547.85[0.00,2.35]52.9655.42Y1130.0044.9148.730.0059.9862.65Y121[0.00,1.12]0.000.00[0.00,2.68]0.000.00Y122[23.15,24.04]0.000.000.000.000.00Y12313.660.000.0050.590.000.00Y13116.270.000.002.490.000.00Y132[29.92,31.80]0.000.00[53.07,53.74]0.000.00Y1330.000.000.00[4.42,6.41]0.000.00Y2134.495.084.55[1.94,2.22]2.191.96Y2234.490.000.00[1.94,2.22]0.000.00Y2334.490.000.00[1.94,2.22]0.000.00Y3110.008.307.520.000.390.35Y3120.008.727.940.000.410.37Y313[11.77,12.90]12.7711.88[0.55,0.60]0.600.55Y322[0.00,0.25]0.000.000.000.000.00Y323[11.77,12.54]0.000.00[0.55,0.60]0.000.00Y333[11.77,12.90]0.000.00[0.55,0.60]0.000.00

(2)單從本文的數(shù)值結(jié)果來看：當(dāng)滿意度水平λi不變、可能度水平βi增大時(shí)，3個(gè)規(guī)劃期內(nèi)的4種常規(guī)能源供應(yīng)量Xi,t(i=1,2,3,4)均有增加，而3種可再生能源發(fā)電量Yj,m,t(j=1,2,3)有增有減，但系統(tǒng)總成本f會(huì)增加，且增幅明顯；當(dāng)可能度水平βi不變、滿意度水平λi增大時(shí)，4種常規(guī)能源供應(yīng)量Xi,t(i=1,2,3,4)不變，而3種可再生能源發(fā)電量Yj,m,t(j=1,2,3)依然有增有減，系統(tǒng)總成本f也會(huì)增加，但增幅較小。可見可能度水平βi比滿意度水平λi對(duì)系統(tǒng)成本影響更大，畢竟λi只存在于含隨機(jī)變量的約束條件(8)和(9)中，而βi存在于含區(qū)間數(shù)的約束條件(3)-(15)中。另外，不管是可能度水平βi還是滿意度水平λi增加(即約束條件的違反度越低)，都會(huì)導(dǎo)致系統(tǒng)總成本增加。這表明能源的安全性和系統(tǒng)的可靠性需付出更高的成本代價(jià)。

(3)由于柴油、汽油的發(fā)電成本較高，在電力需求得到滿足的情況下，不同地區(qū)不同時(shí)期的柴油、汽油的發(fā)電量Yj,m,t(j=4,5)均為0。而3種可再生能源的發(fā)電設(shè)備也無需增容，畢竟增容會(huì)產(chǎn)生額外的巨大增容成本。

4 討論

從計(jì)算和分析結(jié)果來看，本文結(jié)合滿意度方法和可能度方法建立的能源規(guī)劃新模型是合理有效的，其優(yōu)勢(shì)有：①能反映系統(tǒng)中不同能源品種、不同發(fā)電技術(shù)、不同消費(fèi)部門間關(guān)系的復(fù)雜性；②能處理系統(tǒng)中以區(qū)間數(shù)和隨機(jī)變量反映出的不確定性；③考慮了3個(gè)規(guī)劃期內(nèi)發(fā)電廠的增容問題，能反映系統(tǒng)的動(dòng)態(tài)性；④能反映系統(tǒng)成本、能源安全與系統(tǒng)可靠性之間的相互制約關(guān)系；⑤能提供不同約束違反水平下的能源配置方式。

可能度方法的使用解決了文獻(xiàn)[9]中的兩階段子模型可能無解的問題。而作者提出的處理隨機(jī)不等式的滿意度方法，與常用的機(jī)會(huì)約束法[3,6-7]相比，不受隨機(jī)變量具體分布類型的限制，只需知道其兩個(gè)關(guān)鍵數(shù)字特征即可，使用起來更有優(yōu)勢(shì)。

本文模型雖然考慮了3個(gè)地區(qū)在3個(gè)規(guī)劃期的動(dòng)態(tài)規(guī)劃，但由于模型中變量、參數(shù)甚多，以及考慮到便于與文獻(xiàn)[9]比較分析，在算例中沒有細(xì)分3個(gè)地區(qū)能源結(jié)構(gòu)和需求差異。這是本研究的不足之處。在下一步的研究中，可加以改進(jìn)這個(gè)問題，也可以考慮能源消耗的環(huán)境成本、系統(tǒng)的可靠性等建立多目標(biāo)優(yōu)化模型，還可以繼續(xù)探索其他能解決不確定問題的啟發(fā)式算法。本研究結(jié)果可為相關(guān)決策部門在制訂能源系統(tǒng)規(guī)劃方案時(shí)提供理論和方法支持，也可供其他學(xué)者作研究參考。