大跨連續(xù)梁拱組合橋梁拱分擔比例實驗探究
夏文傳 任利鋒2 周智宏2
(1.蘭州交通大學,甘肅 蘭州 730070;2.華邦建投集團股份有限公司,甘肅 蘭州 730070)
一、實驗概況
(一)實驗模型
某黃河大橋跨徑為80m+150m+80m,矢跨比1/5,主梁采用單箱三室。有機玻璃模型以該橋為背景,模型全長440.8cm,主梁跨徑為214.3cm,邊跨跨徑采用113.6cm,截面形式采用單箱三室直腹板截面,如圖1所示;模型中采用21組吊桿,吊桿采用鋼絲,順橋向間距85.7mm,橋面橫橋向間距287mm,如圖2所示。為研究矢跨比、梁拱剛度比,共制作7個有機玻璃模型,如表1所示。分別對每一模型采用1kg、3kg和5kg的力進行索力張拉,共組合成21個模型。
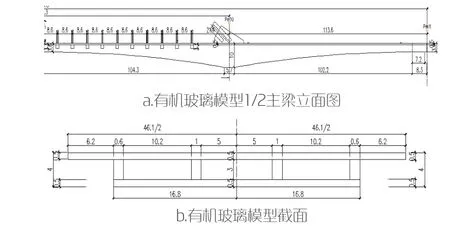
圖1 有機玻璃模型(單位:cm)

圖2 矢跨比1/4.5,剛度比41.2的有機玻璃拱肋截面(單位:cm)
(二)測點布置
實驗過程中位移測量截面有邊跨支座、兩個中跨支座、邊跨跨中、中跨1/4、中跨跨中、1/4拱肋和1/2拱肋共8個截面,每個截面2個測點共16個點的位移;應力測量截面有邊跨跨中、中跨跨中、中跨1/4截面3種,每個截面30個共90個應力測點。
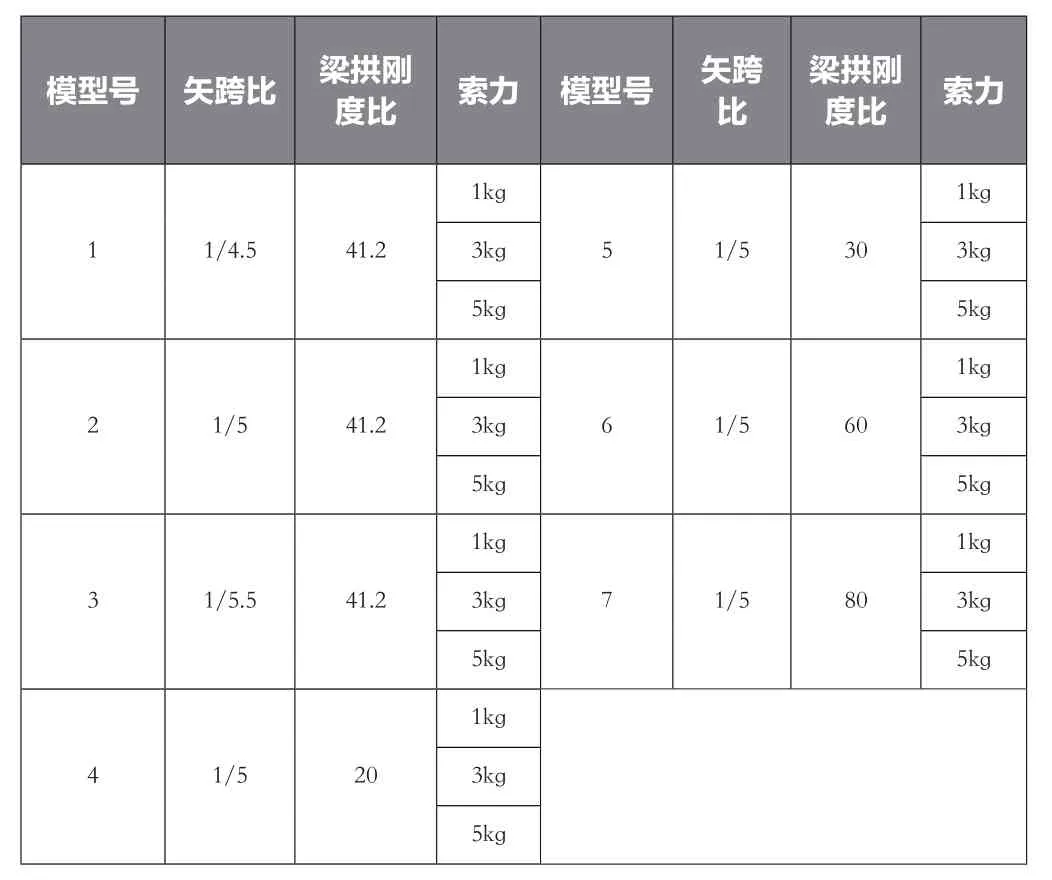
表1 模型參數
(三)實驗工況
實驗工況包括:邊跨跨中截面對稱加載、邊跨跨中截面偏心加載、中跨1/4截面對稱加載、中跨1/4截面偏心加載、中跨跨中截面對稱加載、中跨跨中截面偏心加載。加載荷載大小為40.7kg,實驗圖片如圖3所示。

圖3 實驗加載
模型2(張拉索力5kg時)跨中對稱加載時,實測、有限元及簡化公式計算結果,如表2所示。
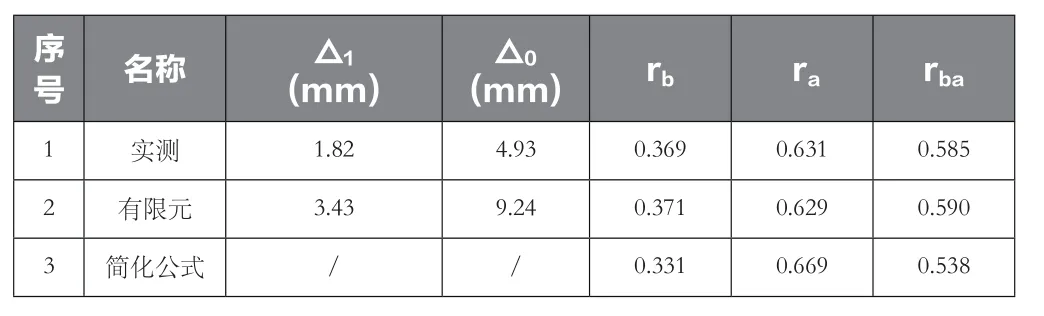
表2 實測、有限元及簡化公式計算結果對比表
由表2可知,實測和有限元結果比較接近,簡化公式與實測和有限元結果誤差較大,誤差為4.2%。簡化公式計算采用變截面連續(xù)梁跨中截面的剛度,剛度比實際模型和有限元模型小,因此梁分擔比例小而拱分擔比例增大。
二、梁、拱分擔荷載比影響因素分析
(一)張拉索力T影響分析
簡化公式中rb與T無關,實測和有限元索力對rb也很小,如圖4所示。
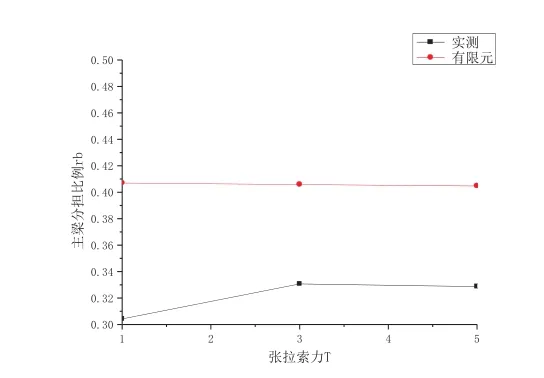
圖4 T與 Kha關系
(二)梁、拱抗彎剛度比Kba影響分析
以rb為因變量,Kba為變量,其余為參數,則公式可簡化為:

簡化公式計算的rb與Kba關系曲線如圖5所示,實驗和有限元得到的rb與Kba關系如圖6所示。從圖5、圖6可以看出,當Kba≤1時,此時拱肋承擔絕大部分荷載,拱肋荷載分擔比較大,而主梁分擔荷載較少,主梁分擔比較小。當48>Kba>1時,rb隨Kba增大而急劇增大。當56>Kba>48之間時,梁拱基本平均分擔荷載。當Kba>56時,此時主梁剛度較大、拱較柔,主梁承擔荷載較多,主梁荷載分擔比超過拱肋荷載分擔比。
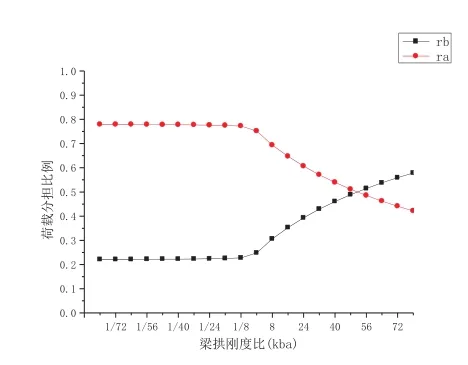
圖5 ra、rb與 kba關系
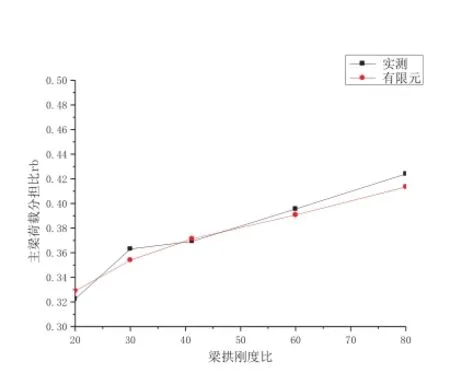
圖6 rb與 kba關系
(三)吊桿、拱肋等代剛度比Ksa影響分析
以rb為因變量,Ksa為變量,其余為參數,則公式可簡寫為:

則rb與Ksa關系曲線,如圖7所示。從圖7可以看出,rb隨Ksa增大而減小;當Ksa<1600時,rb隨Ksa變化急劇;當Ksa>1600時,rb隨Ksa變化較緩。
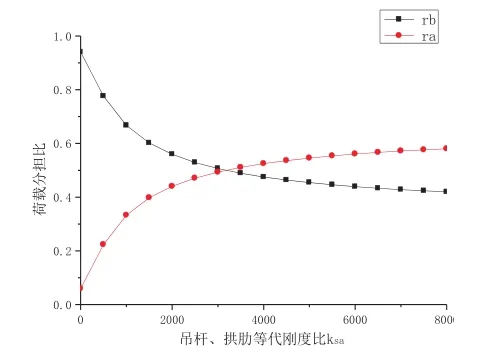
圖7 rb與 ksa關系
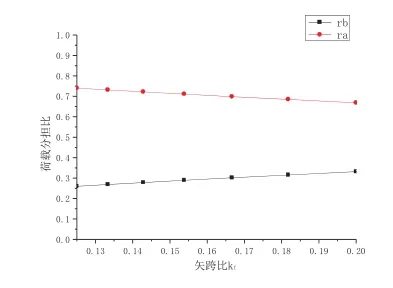
圖8 ra、rb與 kf關系
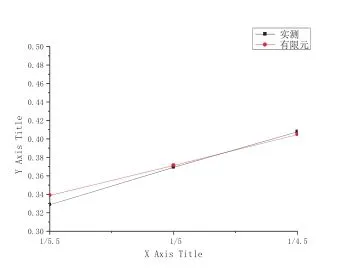
圖9 rb與 kf關系
(四)矢跨比Kf影響
以rb為因變量,Kf為變量,其余為參數,則公式可簡寫為:

簡化公式ra、rb與Kf關系曲線,如圖8所示,實測和有限元得到的rb與Kf關系曲線如圖9所示。從圖11、圖12可以看出,rb隨Kf增大而增大;Kf對rb影響不大。
(五)軸向變形系數Ka影響
以rb為因變量,Ka為變量,其余為參數,則公式可簡寫為:

則rb與Ka關系曲線如圖10所示。從圖13可以看出,rb隨Ka增大而增大。
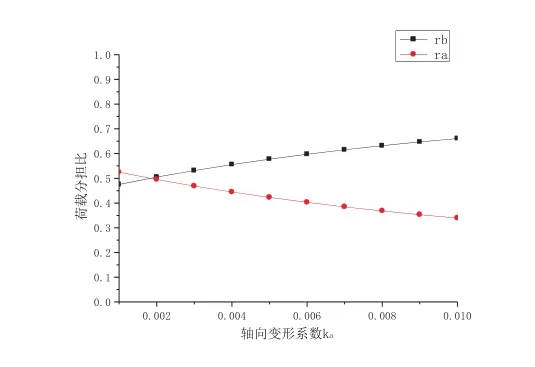
圖10 rb與 ka關系
(六)邊、中跨跨徑比 影響
以rb為因變量,η為變量,其余為參數,則公式可簡寫為:

則rb與η關系曲線如圖11所示。從圖11可以看出,rb隨η增大而增大,但變化不大。
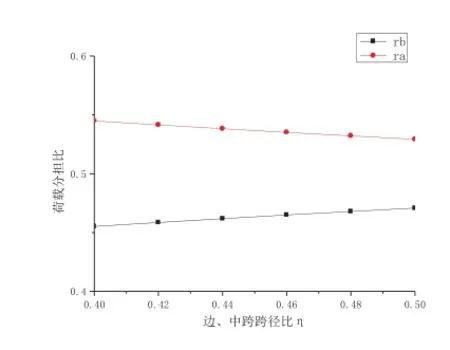
圖11 rb與η關系
三、結語
通過對梁、拱肋荷載分擔比各影響因素的探究可知:
1.采用基于撓度的梁、拱荷載分擔比,能夠較好地反映梁拱組合橋梁拱協作機理;同時基于撓度的梁、拱分擔比能夠利用實橋易于測得的撓度,便于應用于實際工程。
2.當Kba≤1時,此時拱肋承擔絕大部分荷載,拱肋荷載分擔比較大,而主梁分擔荷載較少,主梁分擔比較小。當48>Kba>1 時,rb隨Kba增大而急劇增大。當56>Kba>48之間時,梁拱基本平均分擔荷載。當Kba>56時,此時主梁剛度較大拱較柔,主梁承擔荷載較多,主梁荷載分擔比超過拱肋荷載分擔比。由于條件限制,有機玻璃實驗只做了梁拱剛度比20、30、41.2、60、80,對于其他比例的缺乏實驗數據。
3. rb隨Kf增大而增大,ra隨Kf增大而減小;Kf對rb影響不大。
4. rb隨Ksa增大而減小;當Ksa<1600時,rb隨Ksa變化急劇;當Kba>1600時,rb隨Ksa變化較緩。
5. rb隨Ka增大而增大,ra隨Ka增大而減小。
6. rb隨 增大而減小,但變化不大。
7.張拉索力對rb影響無關。

