基于激光跟蹤儀的火箭橇基準線測量技術研究

張巖龍 狄長春 李建中 吳大林

摘 要 火箭橇軌道基準線是軌道精測和調整的依據，對保證軌道高平直度至關重要。針對現有的基準線測量標校方法存在需要設備多、測量周期長、數據處理復雜等問題，研究基于激光跟蹤儀轉站原理的測量標校技術，能夠解決現有方法的不足。試驗結果表明，該方法的測量精度滿足火箭橇基準線的標校要求，操作簡單，提高了基準線測量標校的效率。

關鍵詞 火箭橇;激光跟蹤儀;基準線;測量

引言

火箭橇是20世紀中后期發展起來的一種大型、高精度地面動態模擬試驗設備，主要用于解決航空、航天、武器裝備及民用高新技術產品在高速度、大過載運行過程中所遇到的一系列性能參數測試難題[1-2]。火箭橇軌道的基準線是軌道測量和調整的依據，是保證火箭橇軌道高直線度的最重要基礎，要求其相對直線度高于1×10-6的空間直線[3]。國內的火箭橇軌道基準線是由間隔60米的一系列基準樁構建空間直線。由于基準樁測量和建設誤差，實際的基準線為一條空間折線（如圖1所示）。其實際直線度遠低于指標，為了保證其直線度，中科院武漢某研究所采用高精度GPS、高精度水準儀和高精度全站儀聯測的方法對基準樁測量，并進行擬合評差對每個基準樁進行修正，提高基準線的直線度以滿足軌道測量要求。中鐵大橋勘測設計院的李書銀[4]等采用GPS和電子水準儀對湖北襄陽某火箭橇軌道基準線進行標校。該標校方法測量過程復雜，使用儀器多，測量周期長，國內能承擔標校任務的單位少，且單次測量費用高。激光跟蹤儀作為大空間高精度測量儀器，通過轉站可實現更大空間的測量。屈亞偉將該技術應用于飛機位姿測量中[5]，林嘉睿將該技術應用于超大型工件研究[6]，這些研究成果表明激光跟蹤儀可用于精確測量大尺寸工作，也為火箭橇基準線標校提供了技術支撐。

1基于激光跟蹤儀的基準線測量原理

激光跟蹤儀作為大空間三維坐標測量儀器，其一次布站測量半徑可達到160m，基準樁測量是要將相距1500m的28個點納入同一個坐標系中，儀器一次架設無法實現所有點測量。為了實現對復雜大型物體的測量，采用轉站方式，利用3～6個空間固定點，實現儀器的多站位測量[6-8]，轉站原理如圖2所示。

儀器在初始位置建立坐標系{A}，對轉站點進行逐一測量，獲取一組點組合P。然后將儀器移動到新的位置，重新初始化，建立新的坐標系{B}，再依次測量轉站點，獲取另一組點組合Q。雖然P和Q兩組是對同一組點的測量，但其坐標值沒有任何關系，因為他們是在不同坐標系中獲取的，坐標系{A}的原點與坐標系{B}的原點不重合，坐標系{A}的方位與坐標系{B}的方位也不重合。

激光跟蹤儀轉站過程就是根據組合P和組合Q兩組點坐標的數值關系，采用公式（1）[9]求解將坐標系B轉換到初始坐標系A的旋轉向量R和平移向量T，實現將坐標系B平移旋轉與坐標系A重合，實現坐標系的統一。這時組合Q與組合P的坐標值就會非常接近，誤差非常小，其誤差與布設距離相關，與儀器的測量精度接近。實現了儀器的移動，儀器在新的位置測量的結果就與初始位置是一樣的。只要在儀器周圍有滿足轉站要求的固定點，這樣的轉站過程可連續進行，實現了將初始坐標系{A}一直擴大到需要的空間。

式中：θ、γ、φ分別為坐標系B相對于坐標系A的俯仰角、滾轉角和偏航角。

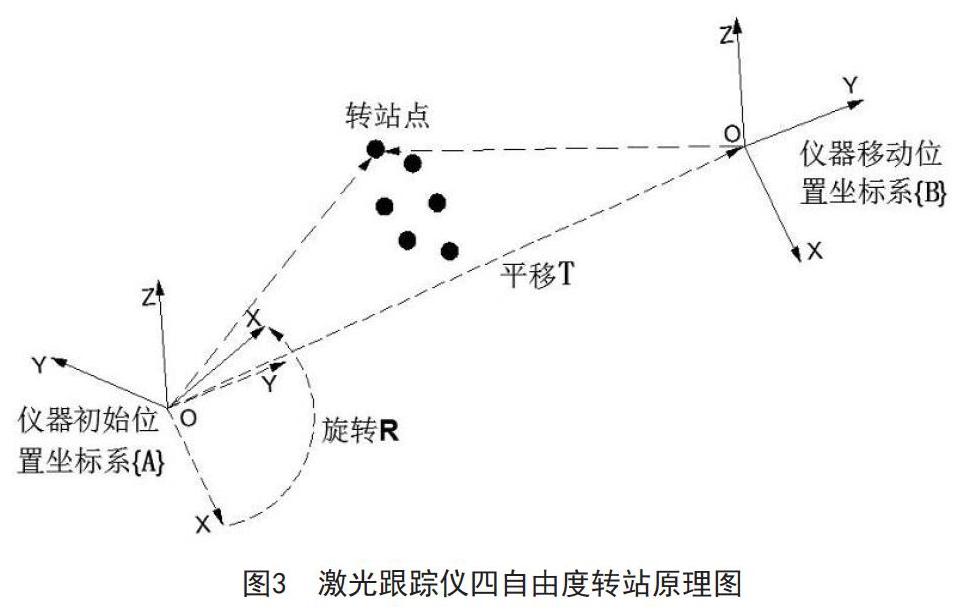
以上轉站過程中，坐標系的平移矩陣T包括X、Y、Z三個自由度，旋轉矩陣R包括RX、RY、RZ三個自由度，而在基準樁測量中，為了保證高程不受影響，還可應用四自由度轉站[10]，其原理如圖3所示。

跟蹤儀不論在任何位置，經過初始化后，儀器是水平的，儀器坐標系的Z軸都是水平面的方向向量，在轉站過程中，平移矩陣T的三個自由度都參與，而旋轉矩陣R只有RZ參與，而RX、RY不參與旋轉，保證基樁高程測量精度。

2基于激光跟蹤儀的基準線測量方法

激光跟蹤儀的測量精度與被測量物距儀器的距離成正比，采用所有測量目標的距離基本相等的，保持同精度測量，通過對現場地形和儀器測量要求分析，建立如圖4的測量方案。

儀器架設于基準線西側的道路，保證與相鄰基準樁和轉站基座的距離相等。步驟如下：

（1）先將跟蹤儀架設于基樁1、2的中間，將轉站基座按要求陣列置于基樁2的側面，測量基樁1、2，再測量轉站基座，保持基座不動;

（2）將儀器移動位置2，先按上次的順序再次測量位置1的轉站基座，對儀器進行最佳擬合轉站操作，完成初始儀器坐標系的平移旋轉，測量基樁3;

（3）將轉站基座按相似的陣形移動位置2，測量所有基座;

（4）將儀器移動位置3，先測量位置2的轉站基座，對儀器進行轉站操作，測量基準樁4，再移動轉站基座，這樣滾動向前，完成所有基樁的測量。

在儀器直線轉站測量方案中，激光跟蹤儀在基樁的單側沿直線移動，還有一種是激光跟蹤儀在基樁的兩側沿折線移動，如圖5所示。儀器可架設于基準線西側的道路和東側的軌道梁水槽內，仍需保證與相鄰基準樁和轉站基座的距離相等。

3試驗驗證與分析

為驗證測量方法的正確性和精度，分別采用激光跟蹤儀直線移動和折線移動兩種方案對基準樁的直線度進行了測量。

3.1 六自由度直線轉站

六自由度直線轉站是指轉站采用六自由度坐標系轉換，激光跟蹤儀直線移動的測量方案。此方案也是第一次測量的方案。結果如表1所示。坐標系建立方法：以J08為坐標原點，J08處的水平面為XOY平面，J08與J23連線為X軸。

從表中可得出，激光跟蹤儀與計量單位測量的X向間距，最大差值為12mm，其次為5.4mm，其余的都較小。高程差的最大差值為46.7mm，并且從J01至J28，變化的趨勢也不同，其變化如圖6所示。電子水準儀測量的高程是J01最低，其余基樁都是不斷升高，與基準線為空間直線的設計是一致的，而激光跟蹤儀測量的高程是從J01開始，先升高，后降低，與基準線的設計不一致。

為此對相鄰基樁高程差進行復測，其結果與計量單位最近測量結果大部分值相近，變化趨勢也一致，變化較大的是兩端基樁高程，這說明絕大部分基準樁的高程并沒有發生較大變化。而六自由度直線轉站測量的高程值相差較大，變化趨勢也不一致，說明此方法精度有待提高。

基樁測量重點需要得到其高程差值和橫向差值，而六自由度轉站中如果繞三個軸旋轉，其初始站的水平面會發生變化，得到的Z向坐標就不是嚴格意義的高程值了，因此考慮只允許繞Z軸旋轉，而禁止其他兩個軸旋轉，即四自由度直線轉站方案。

3.2 四自由度直線轉站方案

采用該方案測量得到基準樁坐標如表2所示。坐標系建立方法：以J07為坐標原點，J07處的水平面為XOY平面，J07與J22連線為X軸。

從表中可得出，對于高程，四自由度直線轉站測量結果與激光跟蹤儀測量結果一致性較好，與電子水準儀測量值大部分比較接近，變化趨勢也一致，只有兩端的相差較大。X向間距，最大差值約為12.6mm，其次為5.2mm，其余的都較小，大部分小于2mm。從以上對比可得出，四自由度直線轉站法對X向和Z向坐標測量是準確的。對于Y向坐標，由于兩種測量方法及坐標系建立方式的不同，Y向間距沒有可比性，為此我們通過多次測量的數據重復性去驗證。表3是應用四自由度直線轉站法進行兩次測量的結果。

從表中可得出，X向和Z向數據重復性較好，X向最大差值僅為1.34mm，78%的差值都小于1mm。Z向最大差值為1.05mm，其余都小于1mm。而Y向差值最大為12.65mm，大于10mm的占36%。

根據李書銀等人撰寫的論文[4]用GPS和全站儀復測的基準樁平面坐標，X向最大為1.7mm，Y向最大為4.7mm，而跟蹤儀復測的Y向差值比較大，需要對測量方案進行改進，減小Y向的差值。

由于軌道基準線的測量是比較困難的，特別是由于場地的限制，儀器的布站條件很有限，X向變化很大，Y向變化很小，轉站過程中測量誤差、計算模型誤差等分配給兩個方向造成的效果差別很大，建立在有限的空間內，加大Y向的變化量，儀器在轉站過程中沿折線移動，即四自由度折線轉站方案。

3.3 四自由度折線轉站方案

在現場對J01～J09號樁進行了測量，其結果如表4所示。

從上表可得出，四自由度折線轉站兩次測量值，X向最大差值為5.52mm，Y向最大差值為3.93mm，Z向最大差值為0.79mm。

為了與四自由度直線轉站方案對比，將兩次全程測量結果的前9個基準樁數據形成表5。

從上表可得出，四自由度直線轉站的兩次測量值，X向最大差值為0.84mm，Y向最大差值為6.31mm，Z向最大差值為0.81mm。比較可得出，折線轉站方案降低了Y向的差值，Z向差值基本不變，但X向差值增大較多。由于X向坐標不參與基準線修正，這也是我們需要的。增加儀器相對基準線的橫向設站距離可減小Y向差值，而X向差值有增大的趨勢，其原因是儀器測量差值是定值，當Z向方向確定后，X向和Y向按一定的比例分配測量誤差，誤差與儀器相鄰測點的距離成反比。從四自由度折線轉站的測量結果來看，增大儀器Y向測量距離對減小Y向誤差有益的，這也為下一步工作提供了思路。

4結束語

針對火箭橇基準線測量難度大、操作煩瑣等問題，研究設計了基于激光跟蹤儀的測量原理與方法，試驗結果表明該方法用于測量基準線具有操作簡便、測量精度高、作業量小、數據處理快等特點。但由于場地條件限制，橫向誤差相對較大，建議下一步繼續研究減少橫向測量誤差的方案。

參考文獻

[1] 楊興邦.XB高精度火箭滑橇實驗滑軌[J].中國工程科學，2002， （10）：98-104.

[2] 楊興邦.火箭橇試驗滑軌[J].航空精密制造技術，1992，（1）：1-3.

[3] 楊興邦.XB火箭橇試驗滑軌的直線度評估[J]. 航空精密制造技術，1999，（5）：25-26.

[4] 李書銀，吳迪軍，李世良. 火箭橇滑軌基準線精密工程測量[J]. 武漢工程職業技術學院學報，2007，（2）：16-18.

[5] 屈亞偉. 基于激光跟蹤儀的飛機位姿測量方法研究[D]. 哈爾濱：哈爾濱工業大學，2015.

[6] 林嘉睿. 大型復雜物體組合測量方法研究[D].天津：天津大學精密儀器與光電子工程學院，2012.

[7] 佚名.徠卡測量系統[ED/OL].https：//baike.baidu.com/item/%E5%BE%95%E5%8D%A1%E6%B5%8B%E9%87%8F%E7%B3%BB%E7%BB%9F/307384？fr=aladdin ，2010.

[8] 佚名.Leaica AT401使用手冊[M].海克斯康測量技術有限公司，2014：15-16.

[9] 金正琪. 提高激光跟蹤儀轉站測量精度的技術研究[D]. 杭州：浙江大學，2013.

[10] 李廣云.LTD500激光跟蹤測量系統原理及應用[J]. 測繪工程，2001，10（4）：3-8.

作者簡介

張巖龍（1982-），陜西子長人;學歷：碩士研究生，工程師，現就職單位：32183部隊，研究方向：武器試驗鑒定工程研究。