常規島建(構)筑物60年設計基準期荷載分項系數研究

章駿華，林少波，陳 飛，干夢軍，張建成，徐 勍，李 萍，呂 平

(華東電力設計院有限公司，上海 200063)

三門核電一期工程采用目前國際上技術最為先進的兩臺AP1000核電機組，規定核電廠的使用壽命為60年，這就要求核電廠的設計使用年限不小于60年，進而確定建(構)筑物設計基準期為60年、而目前我國規范體系的設計基準期為50年，設計使用年限僅考慮了幾種特殊情況，比如5年、50年、100年等。以上分析表明，規范中的分項系數已不能滿足三門核電一期工程的設計要求，本項研究的目的即是針對三門核電一期工程的實際情況，計算與之對應的分項系數，最終使本項工程的建(構)筑物在規定的設計使用年限內滿足《建筑結構可靠度設計統一標準》GB 50068—2001中規定的可靠指標要求。

目前，我國規范的編制采用以概率理論為基礎的極限狀態設計法，以可靠指標度量結構構件的可靠度，采用分項系數的設計表達式進行設計。本文采用了與規范相同的技術路線，但是考慮了三門核電一期工程建(構)筑物的結構特殊性，對目標可靠指標、可變荷載統計參數、可變荷載分項系數等進行了重新計算，從而符合三門核電一期工程的實際設計情況。

當然，基于可靠度的概率極限狀態設計方法十分繁瑣、復雜，現將主要的研究內容簡介如下：

(1)目標可靠指標的選取，采用了目前較為認可的“校準法”，即通過可靠度理論對現行規范的反演計算，得到目前規范隱含的可靠度水平，最終確定目標可靠指標。

(2)根據已有的荷載統計參數，計算60年設計基準期、60年設計使用年限下的荷載統計參數。

(3)假定抗力、恒載等因素不隨時間變化(這是符合規范與實際情況的)，通過調整可變荷載分項系數，使三門核電一期工程建(構)筑物達到預定的可靠度水平。

總之，本項研究既保證了與現有規范的銜接，又滿足了三門核電一期工程實際的特殊要求，有利于工程應用。

1 極限狀態設計表達式

我國規范將極限狀態可分為兩類：(1)承載能力極限狀態：這種極限狀態對應于結構或結構構件達到最大承載能力或不適于繼續承載的變形；(2)正常使用極限狀態。這種極限狀態對應于結構或結構構件達到正常使用或耐久性能的某項規定限值。

對于承載能力極限狀態，規范要求采用荷載效應的基本組合和偶然組合進行設計。對于基本組合的極限狀態設計表達式為：

(1)

(1)由可變荷載效應控制的組合：

(2)

(2)由永久荷載效應控制的組合：

(3)

式中：γG= 1.2；

γQ= 1.4；

SGk,SQk,Rk分別為50年基準期下的恒載、可變荷載效應標準值和抗力標準值。

對于偶然組合，荷載效應組合的設計值宜按下列規定確定:偶然荷載的代表值不乘分項系數；與偶然荷載同時出現的其他荷載可根據觀測資料和工程經驗采用適當的代表值。

對于正常使用極限狀態，應根據不同的設計要求，采用荷載的標準組合、頻遇組合或準永久組合，并應按下列設計表達式進行設計：

S≤C

(4)

式中：C——結構或結構構件達到正常使用要求的規定限值。

對于標準組合，荷載效應組合的設計值S應按下式采用：

(5)

對于頻遇組合，荷載效應組合的設計值S應按下式采用：

(6)

對于準永久組合，荷載效應組合的設計值S可按下式采用：

(7)

采用60年基準期時，承載能力極限狀態下，荷載效應基本組合中的分項系數需根據60年基準期進行調整，此時極限狀態設計值表達式為：

(8)

(1)由可變荷載效應控制的組合：

(9)

(2)由永久荷載效應控制的組合：

(10)

式中：γo= 1.0；

γG= 1.2；

根據可靠度理論計算可變荷載分項系數γQ、SGk,60、SQk,60、Rk,60分別為60年基準期下的恒載、可變荷載和抗力標準值。

2 校核規范中的可靠指標

2.1 校核方法簡介

結構的可靠度是指結構在規定的時間內，在規定的條件下，完成預定功能的概率，可以用失效概率Pf來描述。如果各設計基本變量的理論(真實)概率分布為已知，則可以根據概率的知識求解出失效概率(見圖1)。但在實際工程很難精確掌握各設計基本變量的理論分布，且變量有多個時要進行多重積分存在一定的問題。目前在實用上使用簡化的方法來衡量可靠度。通常利用分布數字的特征——一階原點矩(均值)和二階中心矩(方差)近似描述隨機變量的分布特性，以可靠指標β來表達結構的失效概率。

可靠指標的物理意義：若隨機變量服從正態分布，β的物理意義是從μz到原點以標準差σz為量測單位的距離(見圖1)。可靠指標只與功能函數的均值和標準差有關。

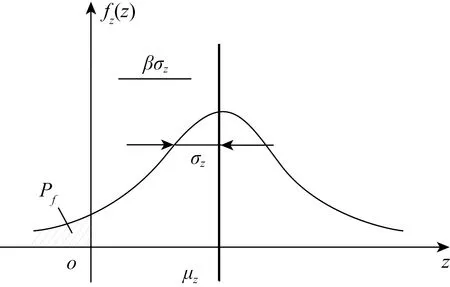
圖1 結構構件可靠指標與失效概率的關系Fig.1 Relationship between reliability index & failure probability of structural components

可靠指標的計算方法選擇：

計算可靠指標的最典型的兩種方法：

(1)中心點法——不考慮基本變量的實際分布，直接假定其服從正態或對數正態分布，導出結構可靠度分析的表達式。由于在分析時采用了泰勒級數在均值(中心點)展開，故簡稱為中心點法。

(2)驗算點法——考慮基本變量的實際分布類型，把非正態分布隨機變量等效化成正態變量，計算可靠指標。由于計算的是設計驗算點的β值，故稱為驗算點法。《建筑結構概率極限狀態設計》(中國建筑工業出版社，1990)第160頁中有這樣一段話：“由西德的拉克維茨(Rackwitz，R.)和菲斯勒(Fiessler，B.)提出的方法，它經系統改進后作為結構安全度聯合委員會(J.C.S.S.)的文件(結構統一標準規范的國際體系第一卷)附錄推薦給土木工程界。這個方法也被很多國家所采納，我國的《建筑結構可靠度設計統一標準》GB 50068—2001也是以該方法作為可靠性校準的基礎。”引文中的“方法”就是驗算點法。

本項研究采用驗算點法，對我國現有規范進行可靠度校核。

目標可靠指標的確定方法通常有三種：①事故類比法；②經濟優化法；③經驗校準法。確定目標可靠指標不僅要考慮理論結果，還要考慮工程設計的現實情況，保證與規范的銜接，以免因為材料用量的過大波動而引起設計人員的不安。在實際應用中，前兩種方法比較困難，規范中對于其目標可靠指標的確定主要采用經驗校準法。本項研究也采取此方法，通過對現行設計規范安全度的校核，利用反演計算，核實出按現有規范設計在結構中隱含的相應可靠指標值，然后分析、調整，最終得到合理的目標可靠指標。

具體校核過程如下：

恒載加一種可變荷載的設計表達式為：

(11)

將公式(11)轉化為用均值表示：

(12)

則：

(13)

而荷載效應比ρ=SQk/SGk、結構重要性系數、各分項系數γ0、γG、γQ、γR各變量的均值系數和變異系數δR、χR、δSG、χSG、δSQ、χSQ都可以查中華人民共和國國家標準《建筑結構設計統一標準》(GBJ 68—84)。

荷載效應的均值、標準差可以由荷載統計參數推算出，抗力的均值、標準差由公式(13)可進一步得到。通過一次二階矩理論，對三種隨機變量進行當量正態化處理，最后根據MATLAB程序得出現行規范分項系數表達式所對應的鋼結構、混凝土構件的可靠指標。

2.2 校核結果

驗算點法校核可靠指標。

根據公式(11)中給出的極限狀態方程，各分項系數取值如表1所示。

本文分別對鋼結構偏心受壓構件、鋼結構軸心受壓構件、混凝土結構構件進行了可靠指標的校核，校核結果如表2和表3所示。

50年設計基準期下混凝土延性結構可靠指標如表4所示， 50年設計基準期下混凝土脆性結構可靠指標如表5所示。

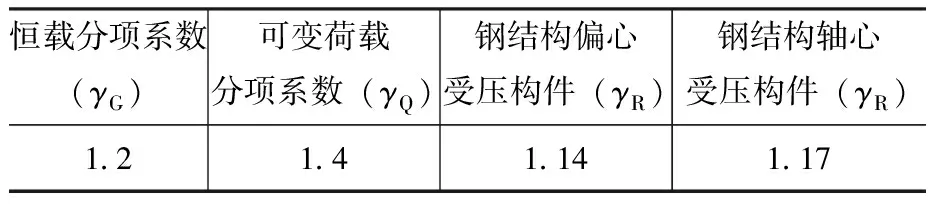
表1 校核規范可靠指標所用分項系數取值

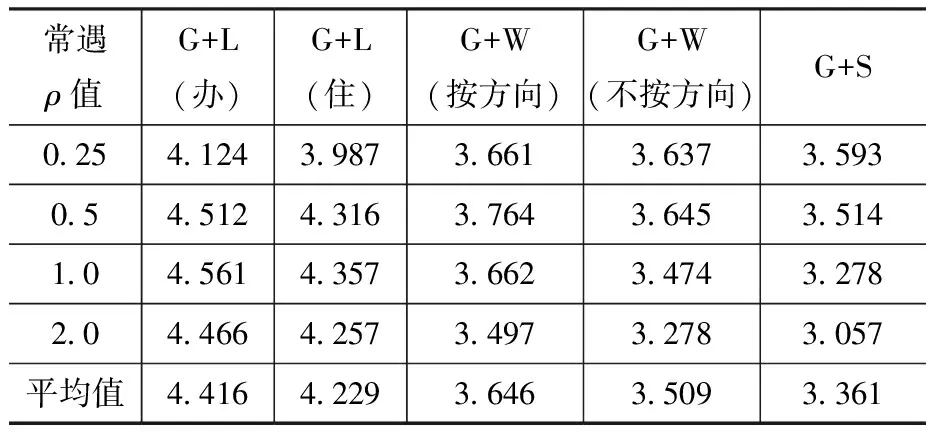
表2 現行規范鋼結構偏心受壓構件可靠指標

表3 現行規范鋼結構軸心受壓構件可靠指標

注：以上兩表中的常用荷載效應比均與中華人民共和國國家標準相同；荷載簡單組合比中華人民共和國國家標準增加了G(恒載)+W(風載)(不按方向)和G(恒載)+S(雪載)兩種情況。

表4 50年設計基準期下混凝土延性結構可靠指標

表5 50年設計基準期下混凝土脆性結構可靠指標

2.3 目標可靠指標取值

根據表2和表3中的計算結果，通過最小二乘法求出最佳的可靠指標為3.93，故建議取目標可靠指標為4.0。

根據表4和表5，對于混凝土結構延性結構，目標可靠指標取為4.0；對于混凝土結構脆性結構目標可靠指標取為4.3。

3 計算60年設計基準期的荷載統計參數

3.1 荷載統計參數修正總原則

在保證60年設計基準期下的荷載保證率與中華人民共和國國家標準GB 50009—2001 《建筑結構荷載規范》50年設計基準期相同的情況下，隨著設計基準期的變化，則荷載標準值、荷載分布的參數(均值、方差)等會發生變化，那么，荷載的均值系數、變異系數必然也跟著發生變化。當使用可靠度理論計算分項系數時，需要在已有荷載統計參數的基礎上調整得到60年荷載統計參數，本文中引用的荷載統計參數源于中華人民共和國國家標準 《建筑結構設計統一標準》(GBJ 68—84)。

既然是基于中華人民共和國國家標準《建筑結構設計統一標準》(GBJ 68—84)的荷載統計參數，保證與中華人民共和國國家標準《建筑結構荷載規范》(GB 50009—2001)相同的荷載保證率計算60年設計基準期的荷載統計參數，那么就有必要對比分析兩本規范與60年設計基準期荷載設置水平的區別：

(1)中華人民共和國國家標準《建筑結構設計統一標準》(GBJ 68—84)、中華人民共和國國家標準《建筑結構荷載規范》(GB 50009—2001)采用的設計基準期為50年，而本項研究的設計基準期為60年；

(2)中華人民共和國國家標準《建筑結構設計統一標準》(GBJ 68—84)采用的樓面荷載的標準值為 ，風、雪荷載的重現期為30年一遇；中華人民共和國國家標準《建筑結構荷載規范》(GB 50009—2001)采用的樓面荷載的標準值為 ，風、雪荷載的重現期為50年一遇；為了保證60年設計基準期下的荷載保證率與中華人民共和國國家標準《建筑結構荷載規范》(GB 50009—2001)50年設計基準期相同，則各類荷載標準值必有所提高。

3.2 計算60年基準期下荷載統計參數

可變荷載是指在設計基準期內其量值隨時間變化，且其變化與平均值相比不可忽略不計的荷載。顯然，可變作用的統計規律是與時間有關的。規范中是將可變荷載化為平穩二項隨機過程{Q(t) ,t∈[0,T]}，假定將荷載隨機過程的樣本函數化為等時段(每一時段長為τ)的矩形波函數，任一時段上荷載的分布函數就是任意時點荷載分布函數，且在不同時段上其概率分布相同，令為FQτ(x)。不同時段上荷載的作用是相互獨立的。則設計基準期T可化為r(r=T/τ)個等時段，每一時段上荷載出現的概率為p，不出現的概率為1-p。

本文主要研究了建筑工程中常用的一些可變荷載，比如樓面活荷載、風荷載(按風向、不按風向)、雪荷載，計算它們在60年設計基準期下荷載標準取值。

根據大量的統計分析，一般假定以上幾種可變荷載均服從極值Ⅰ型分布：

F(x)=exp{-exp[-α(x-u)]}

(14)

u=μ-0.577 2/α

(15)

(16)

(1)樓面活荷載

樓面活荷載可分為樓面持久性荷載(Li)和樓面臨時性荷載(Lr)兩類,調查表明兩者的任意時點的時段均取τ=10年。 《建筑結構設計統一標準》GBJ 68—84的設計基準期為50年，樓面活荷載的標準值為1.5 kN/m2，則住宅樓面活荷載、辦公樓樓面活荷載的保證率分別為79.8%和92.1%；而《建筑結構荷載規范》GB 50009—2001中規定將樓面荷載的標準值提高為2 kN/m2，實際上是將荷載保證率提高了，提高后的住宅樓面活荷載、辦公樓樓面活荷載的保證率分別為97.4%和99.0%。本文即是在住宅樓面活荷載、辦公樓樓面活荷載的保證率分別為97.4%和99.0%荷載設置水平(與現行規范相同)下計算60年基準期下的樓面荷載取值標準。

荷載標準值與設計基準期T內的保證率有這樣的關系：

pk=FL(LkT)=exp{-exp[-α(LkT-β)]}

(17)

所以:

(18)

進一步簡化為:

(19)

故樓面活荷載標準值與其均值、方差有如下關系。

辦公樓荷載：

LkT=μLT+3.14σLT

(20)

住宅樓荷載：

LkT=μLT+2.39σLT

(21)

(22)

σLT=σL

(23)

式中:LkT——設計基準期T對應的樓面荷載標準值；

μLT,σLT——分別為設計基準期T內的均值和標準差；

μL,σL——分別為任意時點的均值和標準差；

m——設計基準期T內荷載平均變動次數。

從表6、表7中可以看出， 60年基準期下的樓面荷載標準值比50年基準期下的荷載標準值大約提高了2%左右。

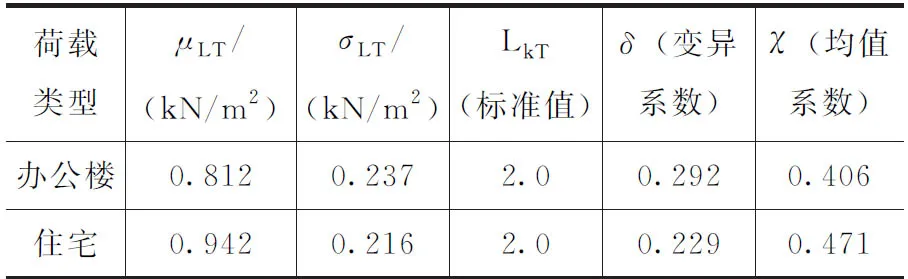
表6 50年設計基準期下樓面荷載統計參數

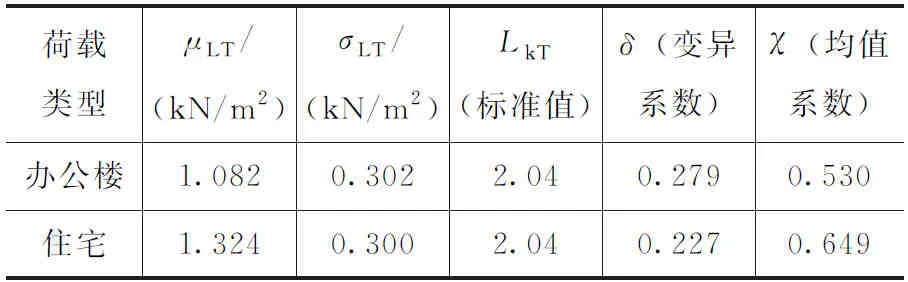
表7 60年設計基準期下樓面荷載統計參數

注：辦公樓樓面荷載標準值實際為2.03 kN/m2，為統一起見，取2.04 kN/m2，偏安全。

(2) 風、雪荷載

根據設計基準期50年內發生超越荷載設計值的概率與60年設計基準期內發生荷載超越設計值的概率一致，即：

FQ,50(Q50,k)=FQ,60(Q60,k)

(24)

式中:FQ,50(),FQ,60(·)——分別為50年、60年設計基準期下風荷載最大值概率分布函數；

Q50,k,Q60,k——分別為50年、60年設計基準期下風荷載的標準值。

計算表明，60年基準期下的風、雪荷載重現期為60年。

與重現期對應的風、雪荷載標準值為：

pk=FQ(Qk)=exp{-exp[-α(Qk-β)]}

(25)

(26)

(27)

式中:μQ,σQ——分別為風荷載年最大值概率分布的均值與標準差；

FQ(·)——風荷載年最大值分布函數；

Qk——風荷載標準值；

Tr——重現期，即Tr年一遇。

根據公式(26)和公式(27)的計算，結論是風荷載的標準值增加了約3%，雪荷載的標準值增加了約4%，具體的修正后的荷載統計參數如表8所示。

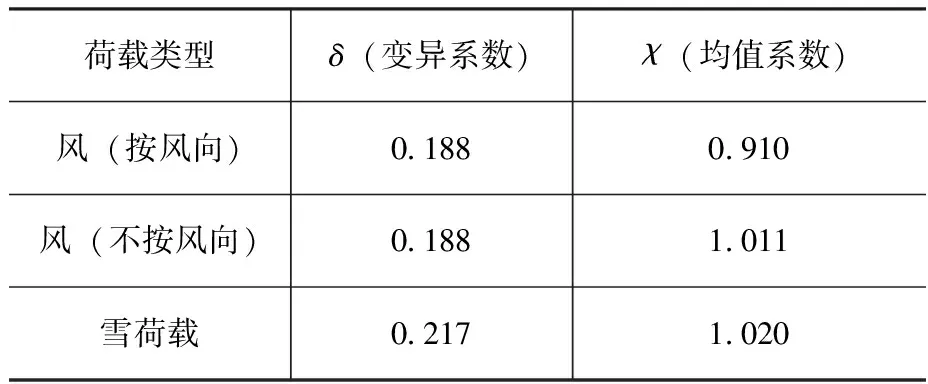
表8 60年基準期下風荷載統計參數

4 根據可靠度理論確定分項系數

4.1 技術路線

本項研究，擬通過調整可變荷載的分項系數使60年設計基準期的三門核電一期工程滿足一定目標可靠指標的要求。也就是說，考慮結構重要性系數不變；抗力、恒載分項系數不變，抗力、恒載不隨時間變化，其統計參數不隨設計基準期的變化而變化。

表9給出了該問題的直觀描述，表10為本文采用的抗力統計參數。

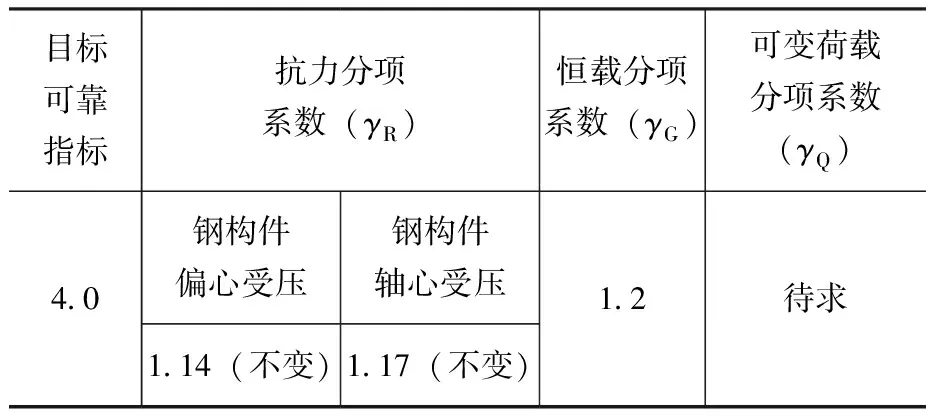
表9 60年設計基準期計算分項系數的直觀描述

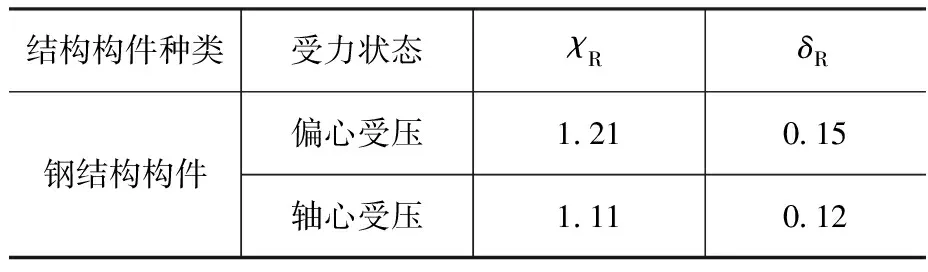
表10 抗力統計參數

4.2 理論說明

結構在設計使用年限T內的功能函數表示如下：

ZT=R-SG-SQT

(28)

設基本變量R、SG、SQT是相互獨立的隨機變量，其中隨機變量R(抗力)服從對數正態分布，隨機變量SG(恒載效應)服從正態分布，隨機變量SQT(可變荷載效應)服從極值I型分布。

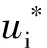
(29)

(30)

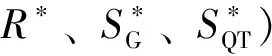
抗力在設計驗算點處當量正態變換后的參數為：

(31)

(32)

恒載效應在設計驗算點處當量正態變換后的參數不變：

σ′SG=σSG

(33)

μ′SG=μSG

(34)

可變荷載效應在設計驗算點處當量正態變換后的參數為：

(35)

(36)

對于功能函數公式(28)、公式(30)可簡化為：

(37)

然后依次代入公式(31)、公式(33)、公式(36)中的參數σ′R、σ′SG、σ′SQT，可以分別求出αR、αSG、αSQT。

可以看出由初始的設計驗算點可以推出與此相對應的各變量的方向余弦，再根據公式(29)和已知的可靠指標，顯然可以推出新的設計驗算點。我們知道在設計驗算點處滿足這樣的條件：

(38)

觀察公式(38)，建立這樣的迭代格式：

(39)

(40)

將公式(38)轉化為實用設計表達式：

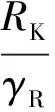
(41)

(42)

最終推出γQ為：

(43)

4.3 60年基準期可變荷載分項系數取值

根據以上理論推導，通過自編的MATLAB程序計算分析得出可變荷載分項系數,如表11和表12所示。

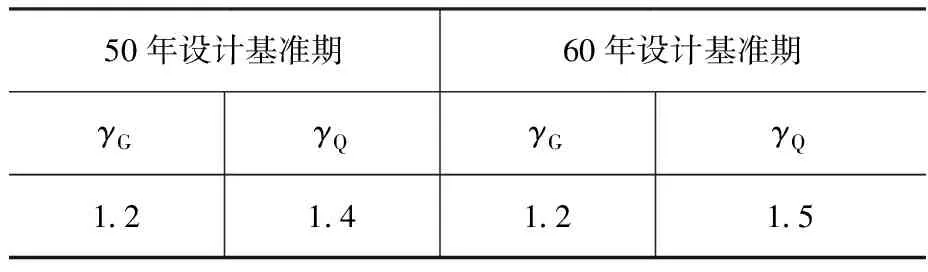
表11 由可變荷載效應控制的組合

表12 由恒載效應控制的組合

5 結論

綜上所述，三門核電一期工程常規島建(構)筑物60年基準期下的荷載分項系數取值是能滿足工程設計需要，使本工程建(構)筑物達到預定的可靠度水平。