雙向應力場下對接接頭裂尖應力強度因子研究*

嚴仁軍 王順清 諶 偉 郝傳奇

(武漢理工大學交通學院 武漢 430063)

0 引 言

工程結構中疲勞裂紋萌生和擴展會導致結構失效.焊趾處表面裂紋的萌生和擴展就是潛艇錐柱結合殼破壞乃至斷裂的主要原因之一[1].因此，選擇合理的應力強度因子計算式來預測裂紋擴展速率，進而估算疲勞裂紋擴展壽命就顯得尤為重要.

本文分析了對接接頭焊趾附近裂紋尖端的應力狀態，考慮對接接頭焊趾幾何形狀、裂紋附近焊接殘余應力以及壓彎雙向應力等因素對現有的應力強度因子經驗公式進行修正.并根據現有的疲勞裂紋擴展模型對該類型結構的疲勞裂紋擴展速率進行預測，驗證修正的等效應力強度因子計算方法的適用性.

1 雙向應力場下表面裂紋應力狀態分析

對于在雙軸拉伸和壓縮載荷下的裂紋擴展行為，國內外也有一些學者做了相應的研究.Smith等[2]對十字形試件(HY100鋼)進行了雙軸拉伸和壓縮疲勞試驗.文中指出與裂紋平行的拉應力可以降低裂紋擴展的速度，而壓應力將加速裂紋擴展.同樣的，Hong等[3]通過十字試件對雙軸疲勞進行了一系列研究，并提出了一種新的應力強度因子計算公式.為了更清楚的了解錐柱結合處的雙向應力狀態，在以上研究的基礎上，通過文獻[4]中的三組含初始缺陷的對接接頭壓彎試驗,見圖1.三組試驗中的對接接頭分別受彎曲載荷Py，彎曲載荷Py和縱向壓縮載荷Px，彎曲載荷Py和垂向壓縮載荷Pz作用，其載荷形式和大小見表1.對壓彎雙向載荷作用下的裂紋尖端應力場進行分析.

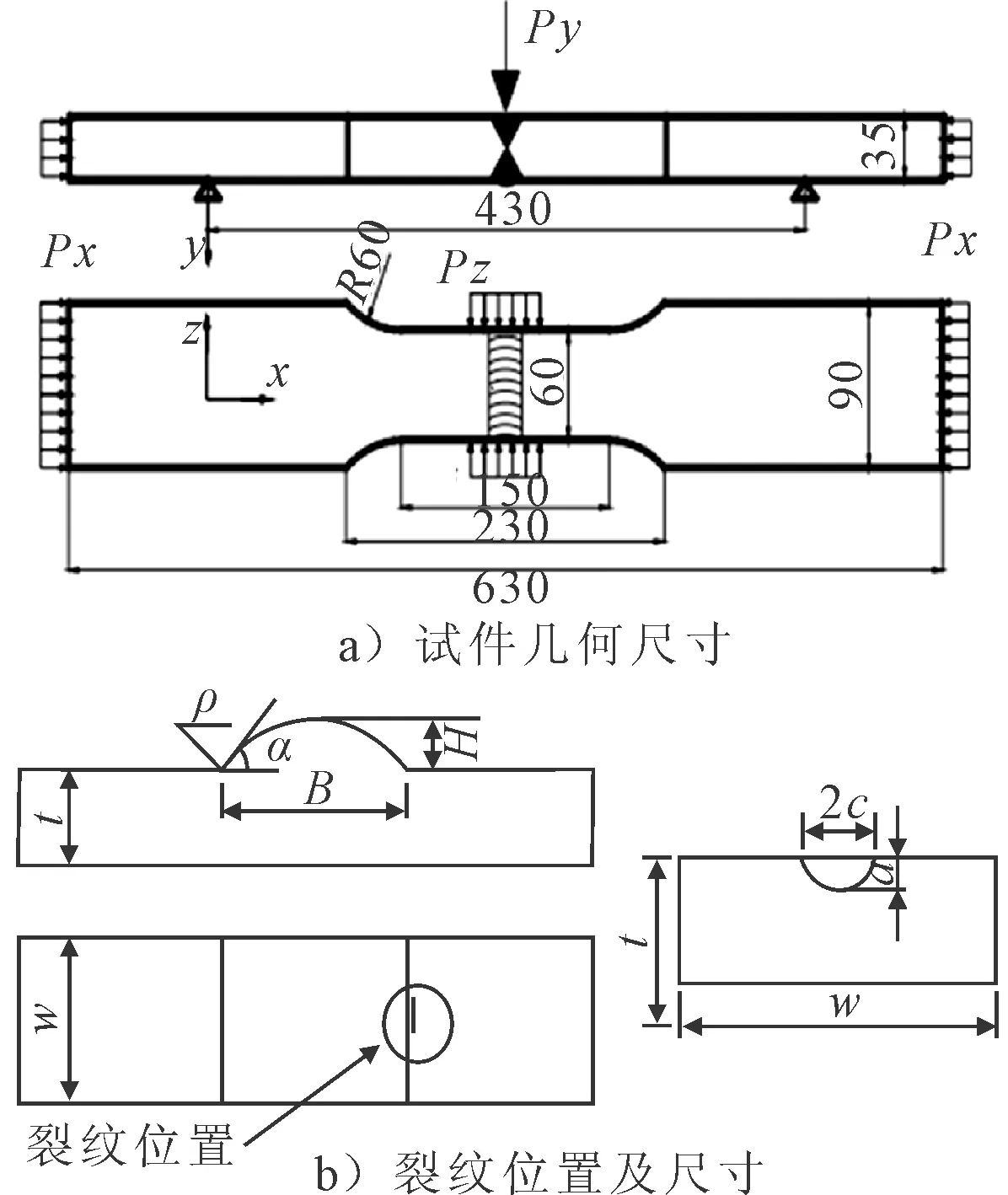
圖1 試件和裂紋幾何尺寸

表1 試件載荷形式 kN

對彎曲載荷、縱向壓縮載荷和垂向壓縮載荷單獨作用下裂紋尖端的應力狀態進行分析.裂紋前緣受力狀態見圖2，定義垂直于裂紋面為X軸，沿裂紋擴展方向為Y軸，裂紋寬度方向為Z軸.當結構分別受彎曲載荷和縱向壓縮載荷單獨作用時，裂紋附近主要受圖2中正應力σx作用，主要是使裂紋面由于受拉而向外擴展；當試件受垂向壓縮載荷時，裂紋附近主要受與Z方向平行的正應力σz作用，其余各方向的正應力和剪應力與σz相比幾乎可以忽略不計.因此，在彎曲載荷和縱向壓載荷作用下，導致裂紋開裂的主要驅動力為垂于裂紋面的正應力σx，在彎載荷和垂向壓載荷作用下，導致裂紋開裂的主要驅動力為垂直于裂紋面的正應力σx和與Z方向平行的正應力σz.

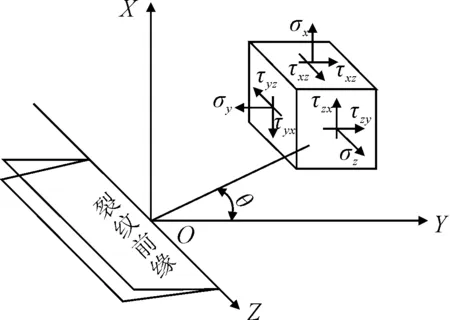
圖2 空間坐標系下裂紋尖端處應力狀態示意圖

2 雙向壓彎載荷下等效SIF計算方法

2.1 縱向壓載荷對應力強度因子的影響

裂紋尖端應力強度因子(SIF)的理論求解十分復雜，在現有的求解SIF的公式中，大部分經驗公式都是在單軸載荷作用下提出的，適用于雙向壓彎載荷情況下SIF的經驗公式還比較少，且大都有一定的局限性.Newman[5]提出了計算拉彎組合應力狀態下平板結構裂紋尖端SIF的經驗公式.為了考慮了縱向壓應力對SIF的影響，黃小平等[6]在應力強度因子計算方法上進行了壓載荷的修正：

(1)

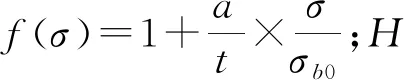
這兩個適用于雙軸載荷作用下的應力強度因子都有一定的局限性：①沒有考慮垂直方向的壓應力(圖1中的Pz作用時結構內部產生的應力)對應力強度因子的影響.②沒有考慮焊趾應力集中和焊接殘余應力對應力強度因子的影響.

2.2 垂向壓載荷對應力強度因子的影響

大量的實驗表明，與裂紋面平行的拉應力會降低裂紋擴展速率，與裂紋面平行的壓應力會增加裂紋擴展速率.然而，經典的線彈性斷裂力學理論中，與裂紋面平行的正應力σz對應力強度因子并沒有影響.針對此問題，一些學者們認為與裂紋面平行的正應力會使裂尖附近的材料屈服，從而導致裂紋尖端發生塑性變形，造成裂紋擴展，適用于線彈性斷裂力學的經驗公式對應力強度因子的計算方法將不再適用.Dugdale[7]引入了塑性修正的SIF計算方法來解釋裂紋尖端小范圍的塑性行為.因此，對于受垂向壓載荷對接接頭，可使用與裂紋尖端塑性相關的應力強度因子計算方法來描述裂紋擴展驅動力：

(2)

式中：Kz為受垂向壓載荷作用下裂紋前緣的應力強度因子，其影響因素包括裂紋形狀以及裂紋尖端所受的正應力；re為固有缺陷的大小，該參數的長度僅為幾微米.對于長裂紋，裂紋長度a與固有缺陷re不是一個數量級.在計算中對re的影響忽略不計.

2.3 焊縫對裂紋尖端應力強度因子的影響

2.3.1焊趾應力集中對SIF的影響

由于焊縫附近的應力集中現象可以通過改變有限元模型的幾何尺寸表現出來.因此，可以建立一系列不同載荷下的對接接頭模型，在有限元模型中細化焊趾處的網格，計算焊趾附近裂紋尖端應力強度因子.并用式(3)來計算焊趾應力集中修正系數.其計算結果見圖3.

Mk=K有焊縫的平板/K無焊縫的平板

(3)

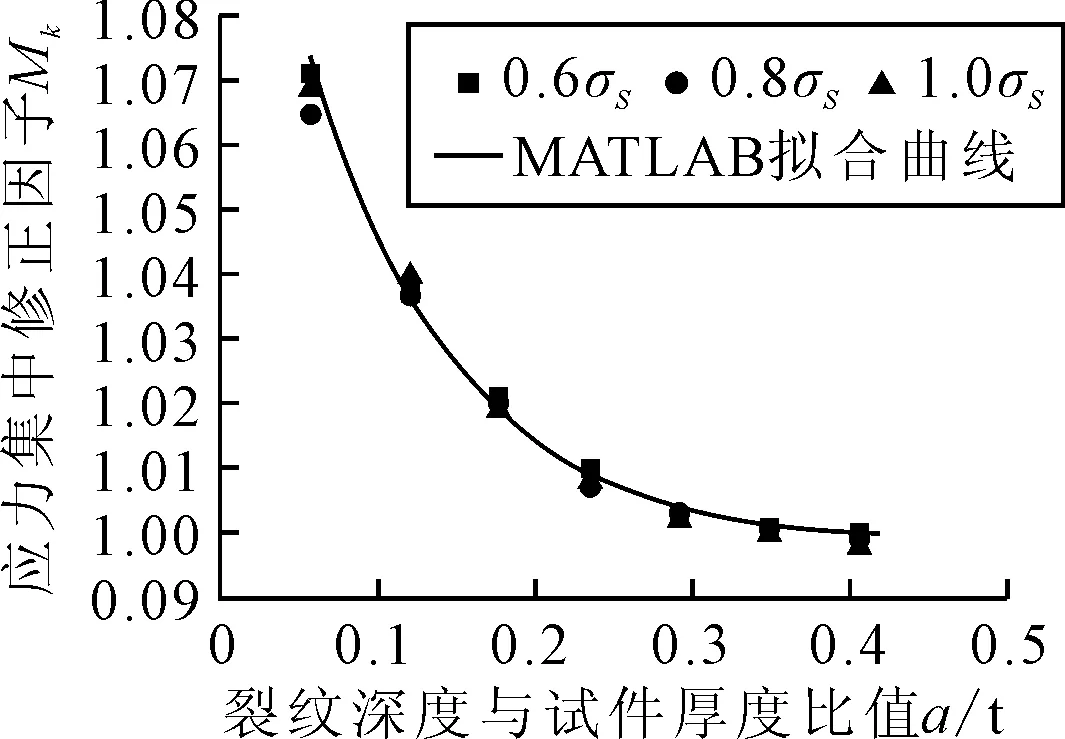
圖3 焊趾應力集中修正因子Mk-a/t曲線

由圖3可知，對于對接結構，當裂紋擴展到一定深度(a/t≥0.24)后焊趾處應力集中修正因子Mk對裂紋幾乎沒有影響.這一結論與文獻[8]的結論相同.因此,對有限元分析結果進行擬合可得出焊趾應力集中修正因子的表達式：

(4)

式中：m=0.999，n=0.141，A=1.82×10-5.

2.3.2焊接殘余應力對SIF的影響

研究發現，在裂紋擴展區域，焊接殘余應力在平行于焊縫方向和垂直于焊縫方向的變化都不是很大.但是對于厚板來說，殘余應力在厚度方向上的影響卻不可忽略.焊接殘余應力沿厚度方向的分布規律，為

(5)

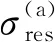
由殘余應力引起的應力強度因子為

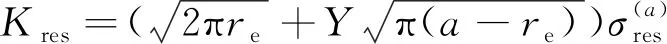
(6)

2.4 雙向壓彎載荷下等效SIF表達式

計算由縱向壓縮載荷和彎曲載荷引起的裂紋尖端應力強度因子時，在縱向壓載荷和彎曲載荷作用下，裂紋前緣受垂直于裂紋面的正應力σx作用，此時可認為裂紋是純I型裂紋，其裂紋尖端應力強度因子為I型.計算由垂向壓縮正應力引起的裂紋尖端應力強度因子時，考慮垂向壓縮正應力對雙軸疲勞裂紋擴展的影響是由塑性誘發的，因此，對垂向壓縮正應力引起的裂紋尖端應力強度因子可單獨計算.殘余應力是由于焊接造成的，且在焊接結束后，結構內部的焊接殘余應力就不會再改變了.因此，在考慮焊接殘余應力造成的應力強度因子時，也可以單獨進行計算.再結合焊趾附近應力集中對裂紋尖端應力強度因子的影響.可將垂向壓彎載荷作用下，焊接結構裂紋表面的應力強度因子公式做如下修正：

Keq=MKKI+Kz+Kres

(7)

式中：KI為縱向壓縮和彎曲載荷作用下表面裂紋前緣的應力強度因子；Kz為垂向壓載荷作用時表面裂紋前緣的應力強度因子；Kres為由殘余應力引起的表面裂紋前緣的應力強度因子.

3 改進的等效應力強度因子模型適用性分析

3.1 疲勞裂紋擴展速率模型

在斷裂力學中，可以用應力強度因子幅值ΔK來描述疲勞裂紋的擴展速率da/dN.經典的Paris模型基于大量的試驗結果進行總結并提出，對裂紋擴展速率擬合精度最高.因此，本文選用Paris模型對裂紋擴展速率進行預測.

為了在計算中考慮垂向壓縮正應力、焊接殘余應力等對裂紋擴展速率的影響，使用改進的等效應力強度因子幅值ΔKeq代替Paris公式里的應力強度因子幅值.其裂紋擴展速率和應力強度因子幅值曲線可以表示為

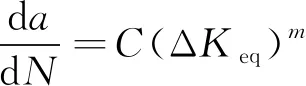
(8)

式中：ΔKeq=Keqmax-Keqmin；a為裂紋長度；N為裂紋處應力循環次數；da/dN為疲勞裂紋的擴展速率；C，m為材料參數.

3.2 實驗驗證

為了直觀的看出裂紋擴展速率與裂紋深度的關系，根據修正的等效SIF計算方法(見式7)和Newman經驗公式分別對三種載荷形式的對接接頭裂紋尖端應力強度因子幅值進行計算，并繪制da/dN隨裂紋深度a變化的曲線，見圖4.

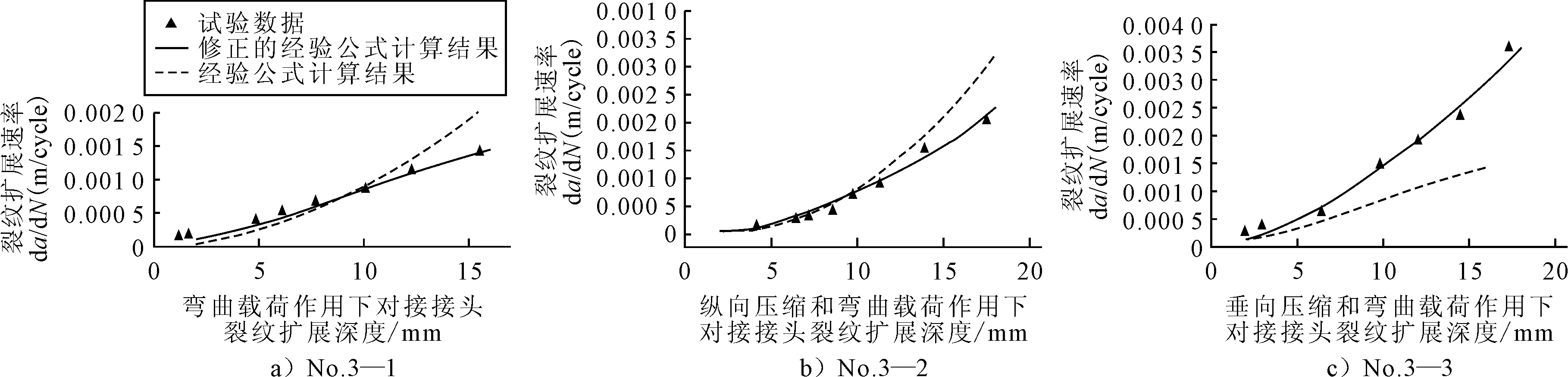
圖4 裂紋擴展速率隨裂紋擴展深度變化曲線

由圖4a)～b)可知，在單軸純彎和縱向壓彎載荷用下，修正的等效SIF計算方法與Newman提出的經驗公式相比，在裂紋擴展后期與實驗數據吻合度更高.這是因為在板中間部分，焊接殘余應力變為壓縮應力，大大降低了裂紋尖端的應力強度因子，從而降低了裂紋擴展速率.

由圖4c)可知，修正的等效SIF計算方法考慮不僅考慮了焊接殘余應力和焊趾的應力集中，更是考慮了垂向壓縮正應力對裂紋擴展驅動力的影響，更好地反映了垂向壓彎載荷作用下結構焊趾附近裂紋的擴展速率.

4 結 論

1) 對于焊接結構，在計算其裂紋尖端應力強度因子時，不能忽略焊接過程中焊接殘余應力對焊縫附近應力場的影響.

2) 一般而言，壓縮應力會導致裂紋閉合，但如果只考慮彎曲應力的影響，在計算上必然會有一些誤差.對于受雙向壓彎載荷作用的對接接頭(包括縱向壓縮和垂向壓縮)，壓縮載荷會加速裂紋沿深度方向的擴展，在計算疲勞裂紋擴展速率時不可忽略.

3) 基于改進的等效應力強度因子計算公式，結合Paris模型對雙向應力場下對接接頭疲勞裂紋擴展速率進行分析，驗證了雙向壓彎載荷作用下等效應力強度因子計算公式的適用性.

4) 改進的等效應力強度因子計算方法對此類結構裂紋擴展速率的計算有較高精度，有望能進一步應用于實際工程當中.