Prophet框架下生產物流運輸節點的阻塞預警方法*

曹小華 劉道凡 涂圣才

(武漢理工大學物流工程學院 武漢 430063)

0 引 言

生產物流自動化系統可以實現不同場地、工序或設備之間物料等的傳送.既定生產物流系統中各環節本身及彼此間的依賴關系在短期內難以調整.通常各環節都遵循生產計劃，工作進程合理有序，但仍會出現異常情況，如數據錯誤、設備故障、人為失誤或業務變動.張俊[1]提出了裝配生產過程的實時狀態模型，應用RFID(射頻識別)技術進行實時數據采集，實現了電子看板的實時生產數據可視化.趙浩然等[2]分析了數字孿生車間與三維可視化監控之間的關系，提出一種三維可視化監控模式和實時數據驅動的虛擬車間運行模式.Cao等[3]建立了RFID數據的計算模型以獲取多屬性生產物流的狀態數據，提出了一種相似度模型表征狀態特征，結合聚類方法挖掘出生產物流中的異常.

關于生產物流的異常問題目前多采用實時監控的方案，即基于既定事實進行狀態判別.對于生產物流運輸路徑的阻塞異常，尚未形成提前預警的成熟方案，實現阻塞提前預警可避免因既定異常而導致經濟損失.在復雜設備的故障診斷領域，利用有效的時間序列預測模型進行故障預警是一種可行的方案[4].

關于時序預測的研究主要有：①時域分析法，如ARIMA(求和自回歸滑動平均)和ARCH(自回歸條件異方差)[5-6]；②頻域分析法，常見如傅里葉變換；③基于機器學習的方法，如BP神經網絡[7]和LSTM(長短時記憶神經網絡)[8]等.不同算法性能各異，同時大多數算法的預測精度隨步長增加而顯著下降.

為了實現對物流運輸節點阻塞異常的預警，建立了描述運輸節點阻塞的預警模型，并提出一種基于Prophet框架的流速度預測方法，基于實際生產物流系統中采集的不同情況下的數據，實現了對運輸路徑的流入/流出速度的有效預測，驗證了該預測方法用于阻塞異常預警的有效性.

1 物流運輸節點的阻塞預警模型

一個典型的物流運輸節點見圖1，其具有n個輸入流和m個輸出流，緩沖容量為b.在運輸節點處，定義輸入流的流入速度vin；在單位時間內流入該節點的產品數量，定義輸出流的流出速度vout；在單位時間內流出該節點的產品數量.

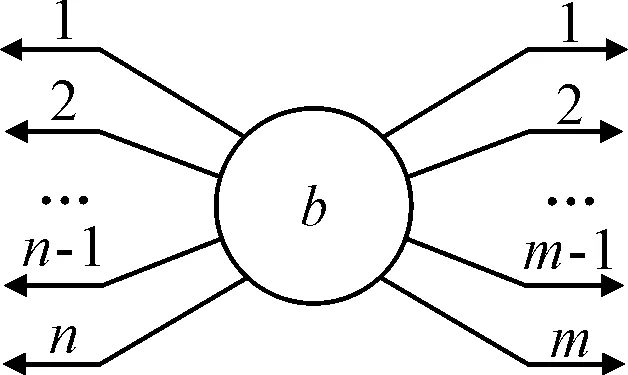
圖1 典型的物流運輸節點

多流入多流出節點和輸入/輸出流的典型實例是生產物流系統中的緩存區和自動化輸送線.假設當前時刻為tcurr，緩沖容量為bcurr，則在任意時刻t(t≥tcurr)，運輸節點的凈流入量為

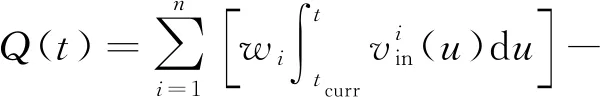
(1)

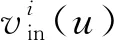
將式按等時間間隔Δt離散化，得到離散化式.

(2)

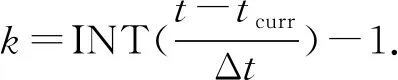
阻塞預警模型為

Δ(t)=bcurr-Q(t)-bthre

(3)

式中：bthre為設定的緩沖容量閾值.當Δ(t)<0時發生阻塞.

在當前時刻tcurr若能預測tcurr～t時間段內的流入與流出速度，即可預算出累積運輸量，再根據式對未來t時刻的節點阻塞狀態進行提前預警.定義阻塞預警提前期為

L=t-tcurr

(4)

2 流速度預測方法

在阻塞預警模型的基礎上，將提出基于Prophet框架的流入/流出速度的預測方法，該預測方法的輸入是tcurr時刻前流入/流出速度的歷史序列，輸出是阻塞預警提前期L時段內流入/流出速度的預測序列.此后用流速度v來統一表示vin和vout.

2.1 數據預處理

在實際生產過程中，RFID等設備會記錄下每個產品流入/流出節點的時間點，見表1.表1前兩列是2018年11月14日某物流公司的某運輸節點處每一批(20個)產品流入該節點的時間點.但是從表1前兩列無法直接得到適用于Prophet的流速度序列.

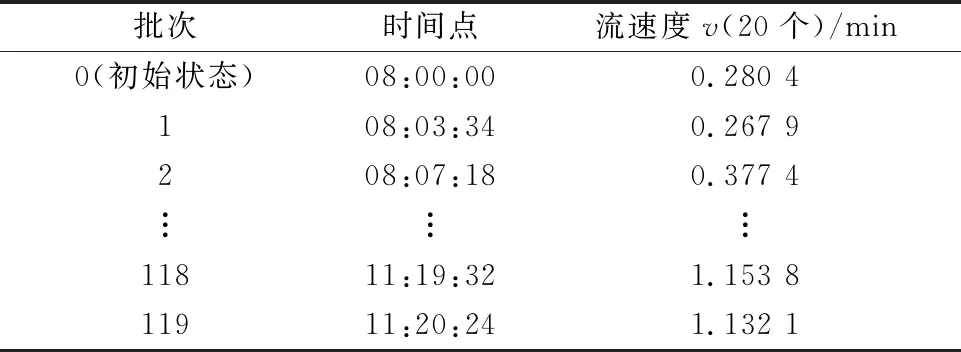
表1 每批產品流入節點的時間點及流速度序列

2.1.1數據轉換

為了得到流速度序列，把相鄰兩批產品流入節點的時間差定義為時間間隔Δti，即

Δti=ti+1-ti

(5)

式中：ti為第i批產品流入節點的時間點，s/(20個).

定義t=ti時刻該輸入流的流速度為

(6)

式中：v(ti)的單位為(20個)/min.得到流速度v的非等間隔的時間序列{v(ti),i=0,1,…,n}，見表1第三列.

2.1.2等間隔化

適用于非等間隔序列的直接建模方法較少且不易實現[9]，采用分段三次Hermite插值法得到等間隔數據.將上節得到的非等間隔的流速度序列{v(ti)}去除掉絕對時間信息，得到序列{u(t)}，即u(t)=v(t+t1)，見圖2中樣本節點.對于數據點集{(xk,yk),k=1,2,…,n}，在相鄰兩個節點所構成的每個子段[xk,xk+1]上定義插值函數H3(x)，即插值點x所對應的值為

(7)

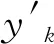
(8)

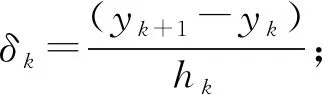
端點x1和xn處的一階導數值則取為相鄰區段一階差商的3倍.對于數據點集{(t,u(t)),t=0,t2-t1,…,tn-t1}，從t=0開始以步長h=60 s作插值點進行插值，得到結果見圖2.將等間隔數據點集恢復絕對時間信息得到等間隔化流速度序列{v(t),t=t1,60+t1,…,60l+t1}，即v(t)=H3(t-t1)，見圖3.

2.2 基于Prophet框架的流速度預測模型

由圖3可知，流速度序列呈上升趨勢并伴有波動，這可能是多種因素導致的，提出一種基于Prophet框架的流速度預測模型，該方法只考慮流速度自身隨時間的變化.Prophet算法的基本思想是擬合歷史數據的相關特性以學習出數據的走向.根據Cramer分解定理，時間序列可表示為[10]

y(t)=g(t)+s(t)+h(t)+εt

(9)

式中：y(t)為時間序列在時刻t的觀測值；趨勢項g(t)為序列的總體變化趨勢；周期項s(t)為季節項，體現出序列的周期循環性質；節假日項h(t)為有規律的突發事件效應；高斯白噪聲εt具有隨機平穩特征，已無可提取的信息.

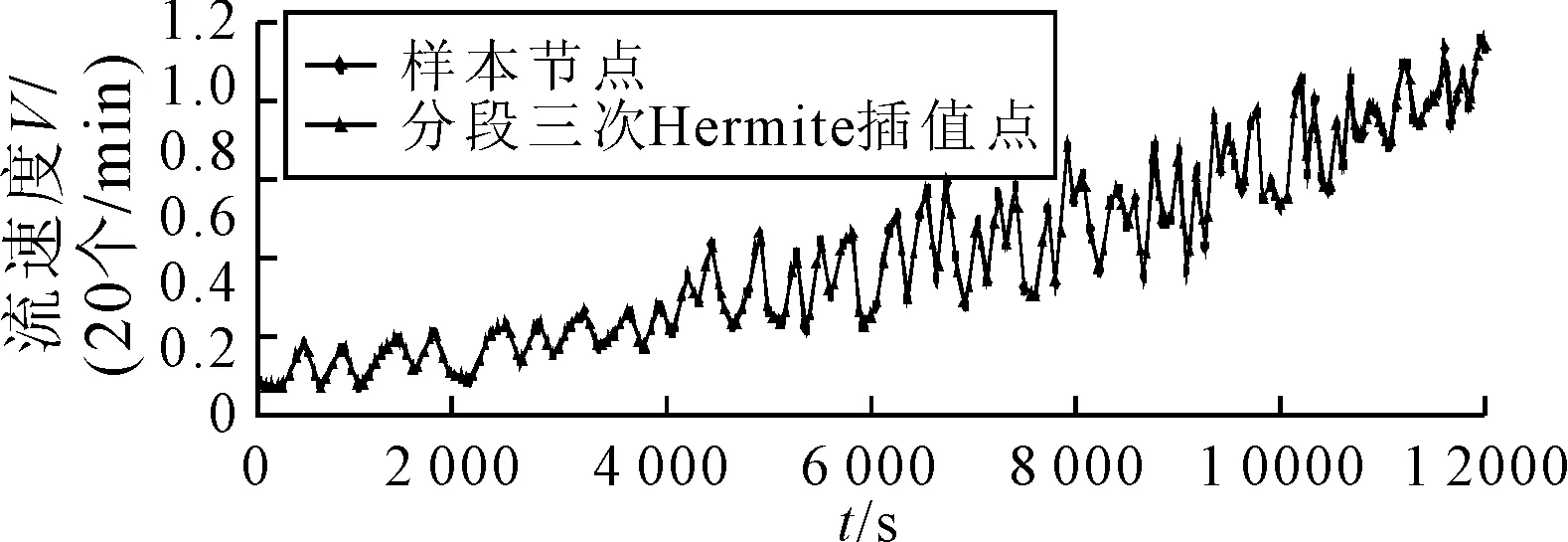
圖2 分段三次Hermite等間隔化插值結果

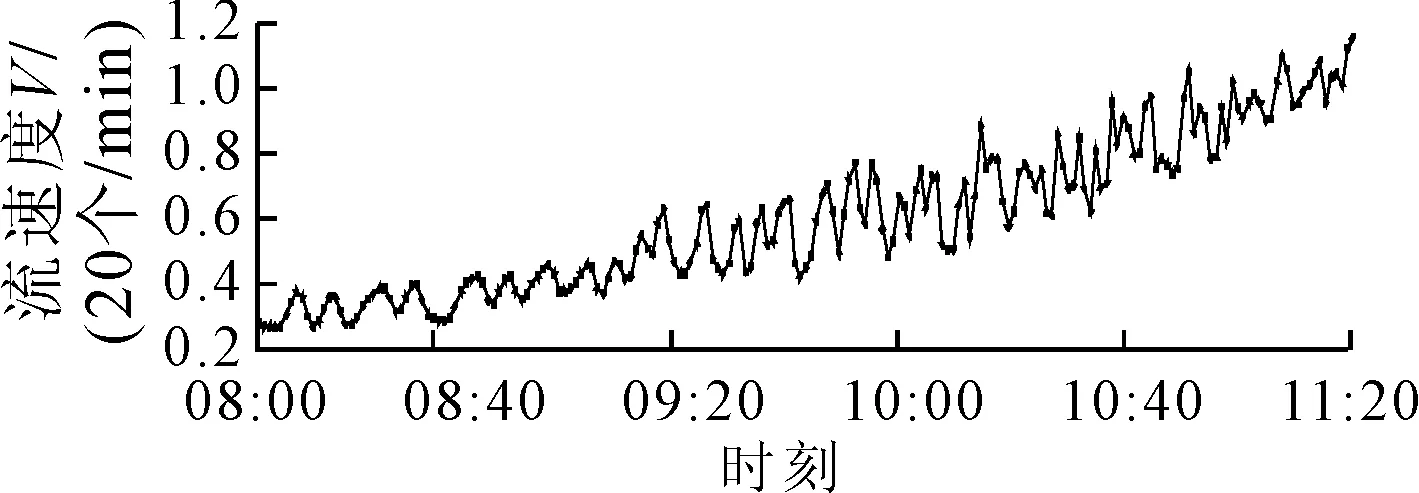
圖3 等間隔化的流速度序列

結合實際情況，剔除節假日項h(t)，將y(t)表示為

y(t)=g(t)+s(t)+εt

(10)

2.2.1趨勢項模型

Prophet算法中趨勢項的核心函數是邏輯回歸函數和分段線性函數.這里采用基于分段線性函數的趨勢項模型.對于線性函數式，將斜率(增長率)項k0與偏置項b0稍加改造得到分段線性函數式.

g(t)=k0t+b0

(11)

g(t)=k(t)·t+b(t)

(12)

斜率項k(t)處于變化狀態且未知待求，因此需從歷史數據中檢測出斜率突變的點.考慮在序列樣本的時間跨度T內設置m個變點sj(j=1,2,…,m)，構成變點向量S.默認在80%樣本數據量內均勻設置25個變點.在變點sj處斜率的增量定義為δj，構成斜率增量列向量δ∈Rm.于是，斜率函數

(13)

將其寫成更簡潔的向量形式

k(t)=k0+a(t)Tδ

(14)

式中：列向量a(t)∈{0,1}m的元素aj(t)滿足

(15)

考慮到變點造成的函數值的非連續性，需對偏置項b(t)做出調整，調整后的偏置項為

b(t)=b0+a(t)Tγ

(16)

式中：列向量γ={γj(j=1,2,…,m)}m，并且γj=-sjδj.

于是基于分段線性函數的趨勢項模型改造為

g(t)=[k0+a(t)Tδ]t+[b0+a(t)Tγ]

(17)

參數δj是未知的，為防止g(t)發生過擬合現象，需加入稀疏先驗對模型進行L1正則化，因此δ～Laplace(0,τ).τ的默認值為0.05，其值較大時模型可適應較大的增長趨勢，但同時也將增加預測值的不確定性.

2.2.2季節周期性

考慮周期項s(t)，將周期項s(t)用有限階的離散傅里葉級數近似表示，即

(18)

式中：P為序列的周期；N為展開的階數；β=[a1,b1,…,aN,bN]T為待估計的參數向量.如果令

(19)

則s(t)為

s(t)=x(t)β

(20)

同參數向量δ類似，需對模型進行L2正則化，因此β～Normal(0,σ2).σ值的大小體現出其對周期性的調節強度.序列展開階數N相當于對周期項進行低通濾波，會產生截斷誤差，N越大，越能適應更復雜的周期性，但有可能使模型過擬合，可根據AIC等準則對模型進行參數的自動選擇.

3 實驗與結果

預處理后的數據劃分成訓練數據集(時間跨度為T)以及測試數據集(時間跨度為L).將訓練數據輸入預測模型得到時間跨度為L的預測值，并將Prophet模型的預測結果與LSTM和SARIMA(季節求和自回歸滑動平均)的預測結果進行統計對比.

3.1 模型設置與預測結果

預處理后的序列的時間粒度為1 min，共201個數據，前181個為訓練數據，后20個為測試數據.預測模型的參數設置見表2，采用最大后驗估計(MAP)實現參數估計與區間估計.

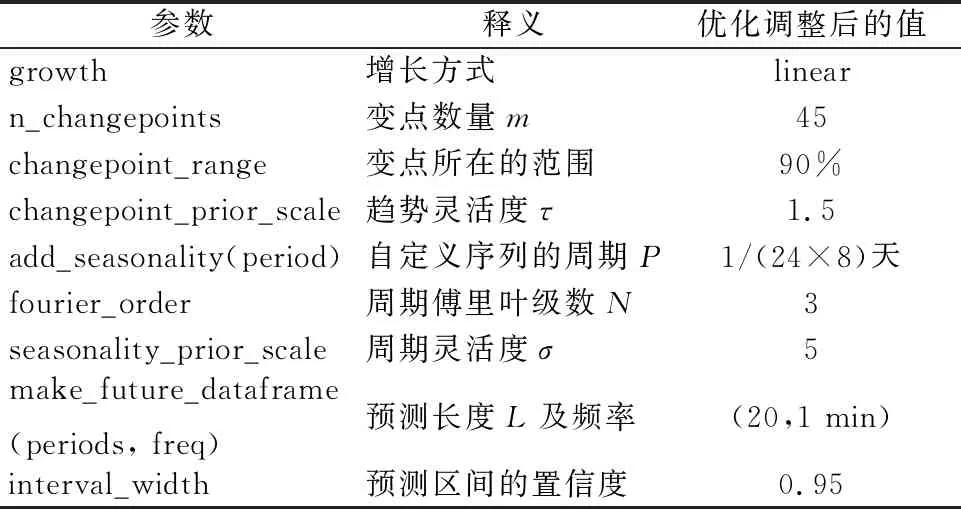
表2 預測模型的參數設置

將訓練數據輸入Prophet模型，提取出流速度序列的組成成分見圖4.圖4a)為序列的總體趨勢走向，圖4b)為序列的周期特征，將兩個成分應用加法得到圖4c)的組合模型，如中間曲線所示，并給出了置信度為0.95下的序列估計區間.圖4c)中折線顯示了變點位置及增長率變化情況.

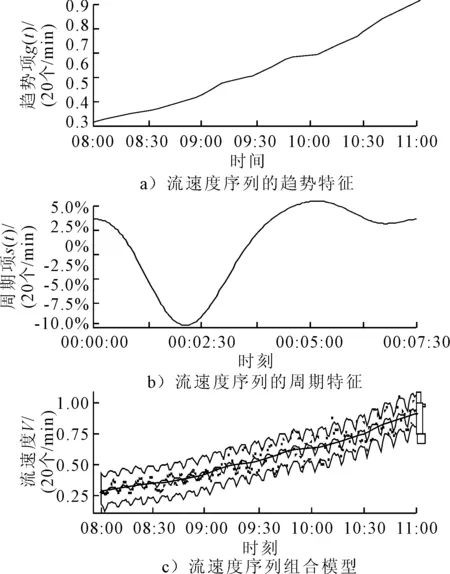
圖4 流速度序列訓練數據集的分解效果

根據從訓練數據中學習到的模型待估參數和序列特征，得到圖5的預測結果.圖5為預測序列的值及置信度為0.95下的序列區間估計值，以及測試序列的實際值.

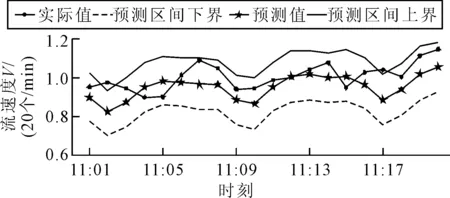
圖5 模型的預測結果

3.2 性能度量指標

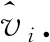
均方根誤差(eRMSE).預測值與實際值差值的向量2范數.

(21)

平均絕對誤差(eMAE).預測值與實際值差值的向量1范數.

(22)

平均絕對百分比誤差(eMAPE)，為絕對誤差與實際值之比的平均值，即

(23)

3.3 實驗結果對比分析

SARIMA的基本思想是對含有趨勢性和周期性的序列進行d階差分與S步差分，若能得到平穩序列則建立自回歸滑動平均模型，并經白噪聲檢驗、模型定階與參數估計、模型檢驗后進行預測，再還原到原始序列的預測值.LSTM實現多步預測的基本思想是先從序列首值開始提取一定長度的序列，并按一定比例切分成輸入數據(即訓練步長)與輸出數據(即標簽)，隨后逐步滾動，提取出多組輸入數據與標簽訓練LSTM網絡，通過LSTM網絡中的遺忘門、輸入門、輸出門及記憶單元來調節網絡記憶狀態，最后經迭代預測得到與測試序列長度相當的預測序列[11].

對于訓練數據，經由一系列建模過程最終確定SARIMA模型為SARIMA(1,0,1)×(1,0,1)10后進行動態預測.LSTM模型的訓練步長與預測步長分別設為40和20，每個LSTM單元的隱含層神經元數設為100，激活函數采用線性整流函數(ReLU)，優化器采用Adam算法，損失函數采用均方誤差(MSE)，訓練次數epochs=100.三種算法的預測結果對比見圖6.

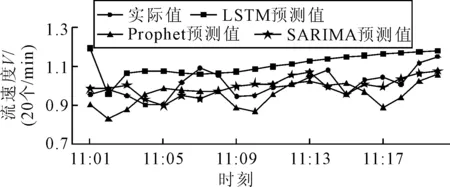
圖6 三種算法的預測結果對比

3種算法的性能指標見表3.由圖6和表3可知，LSTM模型相較于其余兩者并未獲得較好的預測效果；SARIMA與Prophet模型均表現出不錯的效果，各統計指標均不超過1%.從模型結構及建模過程的復雜度來看，Prophet模型最簡潔，LSTM模型最為復雜，SARIMA的建模及模型解釋需相當深厚的專業知識，后兩者都不太適用于物流流速度的預測.

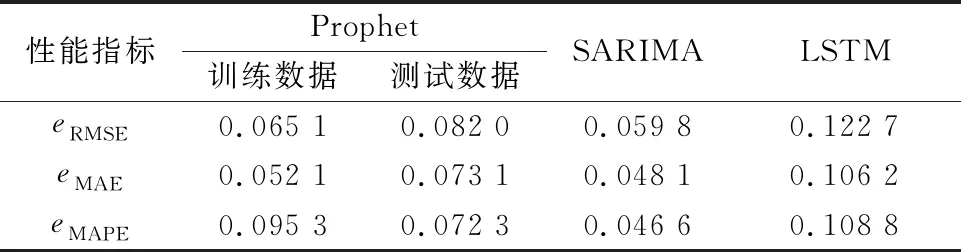
表3 3種算法的性能指標

SARIMA等傳統模型對平穩序列及較弱的非線性序列的分析效果顯著，但是對于存在階躍突變的序列，建模過程變得復雜甚至不可控，預測效果往往不理想.圖7為存在階躍突變的某等間隔流速度序列，Prophet的預測效果優于SARIMA，SARIMA中較優的SARIMA(1,0,0)×(0,0,0)20的預測結果近似于直線，意義不大，說明SARIMA模型不太適用于分段差分平穩序列的預測.

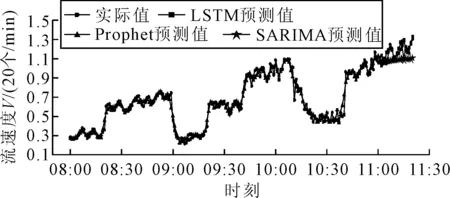
圖7 序列存在突變的預測結果

在測試集上，Prophet方法的eRMSE、eMAE和eMAPE分別為0.063 8，0.048 1和0.042 5，而SARIMA方法的各項指標分別為0.097 4，0.079 9和0.666，均高于Prophet方法.物流生產過程中由于任務訂單變化、生產線突發匯聚或分流，均會出現流速度序列階躍等現象，Prophet模型具有突變點檢測的功能，因此對此類干擾有較強的適應能力，可以獲得較為滿意的預測效果.

4 結 束 語

針對生產物流阻塞異常的問題，建立了表征阻塞狀態的阻塞預警模型，通過預測出各運輸路徑的運輸速度及累積運輸量以實現對該物流運輸節點的阻塞預警.在對原始物流數據進行數據轉換及等間隔化的基礎上，提出了基于Prophet框架的物流運輸節點的流速度預測方法，實驗結果表明該預測方法性能優良，實現了對運輸路徑的流速度的有效預測，并可以適應流速度突變所帶來的影響，性能優于經典的SARIMA和LSTM預測方法.由于所提出的預測模型僅考慮流速度變量隨時間的變化，但是實際生產過程中情況復雜多變，計劃將其他因素引入預測模型，實現更準確地預警.