永磁同步電機積分滑模觀測器控制
柯希彪,郭 琳,4,魯懷偉,袁訓鋒,陳 垚,徐曉龍
(1.商洛學院電子信息與電氣工程學院,陜西 商洛 726000;2.蘭州交通大學自動化與電氣工程學院,甘肅 蘭州 730070;3.商洛市分布式新能源應用技術研究中心,陜西 商洛 726000;4.西安交通大學電力設備電氣絕緣國家重點實驗室,陜西 西安 710049)
0 引言
永磁同步電機(PMSM)具有結構簡單、體積小和效率高等優點,在現代工業制造業等領域應用十分廣泛[1-2]。矢量控制是一種無差控制策略,是永磁同步電機控制應用最為廣泛的控制策略之一,其通過檢測電機相位將定子電流進行交直軸解耦,然后分別對勵磁電流分量和轉矩電流分量進行控制。在矢量控制中,檢測電機相位的精度將直接影響到電機控制性能,通過傳感器可以檢測到電機準確的相位角,但是使控制系統過于復雜,降低了控制系統的抗干擾能力和可靠性,無傳感器控制檢測電機轉子相位和轉速信息成了眾多學者研究的重要課題。
滑模觀測器(SMO)抗干擾性能優良,具有較強的魯棒性,被廣泛應用于永磁同步電機控制系統中。文獻[3-5]通過建立滑模觀測器模型檢測永磁同步電機轉子信息,較好地實現了永磁同步電機無傳感器控制。文獻[6-7]將模糊控制理論引入到滑模控制中,建立了模糊滑模觀測器控制模型,通過模糊控制實時調節滑模控制參數,實現了永磁同步直線電機無傳感器控制。文獻[8-9]分析了典型滑模觀測器產生抖振的原因,通過設計飽和函數對傳統滑模觀測器進行改進,通過仿真分析和實驗驗證表明改進后的滑模觀測器能夠準確估計電機轉速,并且削弱滑模控制的抖振。文獻[10]為了提高六相永磁同步電機的魯棒性,提出一種積分滑模控制算法設計電機調速系統,通過仿真驗證所提出的控制策略的良好性能。文獻[11]為了提高永磁同步電機的控制性能,增強電機控制的抗干擾性,提出了一種永磁同步電機模糊自適應反步積分滑模控制策略,實驗結果驗證了該控制方法的有效性和可行性。文獻[12]將模糊控制引入到模型參考自適應控制中,有效提高了模型參考自適應控制的魯棒性。文獻[13]結合自適應控制理論,通過PI參數實時自適應計算優化模型參考自適應控制,通過仿真驗證了該方法實現了永磁同步電機無傳感器控制。文獻[14]研究了模型參考自適應控制理論通過單一模型無法實現全速度的電機控制,提出了一種分段PI模型參考自適應控制,通過仿真和實驗驗證了該控制策略可以實現電機在全轉速范圍的控制。文獻[15]將滑模控制與模型參考自適應控制相結合,采用雙正切函數代替符號函數設計滑模控制,有效的降低了滑模控制抖振,準確地估算出了電機的轉子位置信息。
本文研究了永磁同步電機傳統滑模觀測器的控制特性,結合積分滑模控制的優點,設計了一種積分滑模觀測器。通過設計飽和函數對滑模控制進行優化,通過建立傳統滑模觀測器控制模型和積分滑模觀測器控制模型,進行仿真驗證。
1 永磁同步電機控制模型
PMSM是一種非線性、強耦合的系統,在搭建數學模型時,為了突出研究問題的主要因素,對電機模型作如下假定:忽略磁路飽和,不計電機鐵損;永磁材料電導率為零;轉子上無阻尼繞組;氣隙磁場呈正弦分布。
隱級式PMSM在兩相旋轉坐標系(d-q軸)的數學模型[2-4,16-17]
(1)
iq和id分別為電機交、直軸電流;uq和ud分別為電機交、直軸電壓;Rs為定子繞組電阻;Ls為電樞等效電感;pm為磁極對數;ωe為電角速度;Ψf為轉子磁鏈;J為轉動慣量;B為粘滯系數;TL為負載轉矩。
PMSM磁鏈方程[2-4]為
(2)
Ψq和Ψd分別為交、直軸磁鏈。
電磁轉矩方程為
(3)
本文所提出的控制是以永磁同步電機雙閉環矢量控制模型為對象展開的,矢量控制是一種無差控制策略,其控制精度較高,結構簡單,是最為常見的PMSM控制模型。
2 永磁同步電機滑模觀測器設計
2.1 永磁同步電機SMO模型
PMSM在兩相坐標系(α-β軸)數學模型[2-4]
(4)
(5)
iα和iβ分別為電機α、β軸電流;uα和uβ分別為電機α軸和β軸電壓;eα和eβ分別為α軸和β軸反電動勢;θe為電機轉子相位角。
滑模觀測器設計
(6)
(7)
“^”代表各狀態量的估算值;K為滑模觀測器開關增益;sgn()為符號函數。
將式(6)與式(4)相減可得滑模觀測器狀態方程為
(8)
當系統達到穩定狀態時,狀態誤差及其變化率均為零:
(9)
電機反電動勢表達式為
(10)
設計滑模面為
(11)
根據Lyapunov穩定性定律可得,為滿足滑模控制可達性要求,滑模增益必須滿足
K>max(|eα|,|eβ|)
(12)
滑模增益K取值須足夠大。K取值過大,滑模觀測器具有較強的抗干擾能力,但運動狀態在滑模面附近會反復大幅變換,使控制系統產生高頻的抖振,降低了控制系統動態品質,不利于系統穩定性要求。SMO模型如圖1所示。

圖1 SMO模型
LPF表示低通濾波器。
由滑模觀測器(SMO)模型可得反電動勢等效模型為
(13)
ωc為低通濾波器(LPF)截止頻率。截止頻率越高,得到的反電動勢含有諧波越多,檢測誤差越大。截止頻率越低,檢測到的反電動勢諧波越少,波形曲線越光滑,反電動勢失真越嚴重,當截止頻率接近或低于電機運行頻率時,將無法檢測到正確的電機反電動勢,從而無法計算出電機的轉子信息。同時低通濾波器會使檢測的相位產生滯后,需要進行一定的相位補償。
通過飽和函數和低通濾波器近似可得永磁同步電機反電動勢,采用反正切法求PMSM相位角和轉速
(14)
Δθ為低通濾波器相位滯后角,當電機轉速越大時,補償角Δθ越大。
采用傳統滑模觀測器檢測反電動勢,系統會引入高頻抖振,低通濾波器濾除高頻抖振,引起檢測相位滯后,需要進行相位補償,通常相位補償是通過反正切函數給出的,增加了控制器的計算量,且又引入了新的不穩定因素。本文通過設計二階的積分滑模觀測器來改善上述問題。
2.2 積分滑模觀測器設計
滑模觀測器模型設計為
(15)
Hα和Hβ為設計的滑模控制律。
式(15)與式(4)相減可得滑模觀測器狀態方程
(16)
設計積分滑模面
(17)
c1和c2均為正常數。
采用指數趨近律
(18)
ε>0,η>0,0<α<1。
滑模觀測器控制律為
(19)
(20)
建立Lyapunov方程
(21)
對式(21)求導可得
(22)
證明所設計積分滑模觀測器滿足Lyapunov穩定條件,所設計觀測器趨于穩定,可用于永磁同步電機控制。
為了減小由符號函數引起的系統抖振,本文設計連續線性飽和函數代替符號函數,飽和函數設計為
(23)
a為正常數,其值決定了飽和函數線性區域內滑模增益的斜率和滑模邊界層厚度。當γ取值滿足式(20)時,滑模觀測器依然滿足Lyapunov穩定條件。
滑模觀測器控制律改寫為
(24)
電機控制模型如圖2所示。
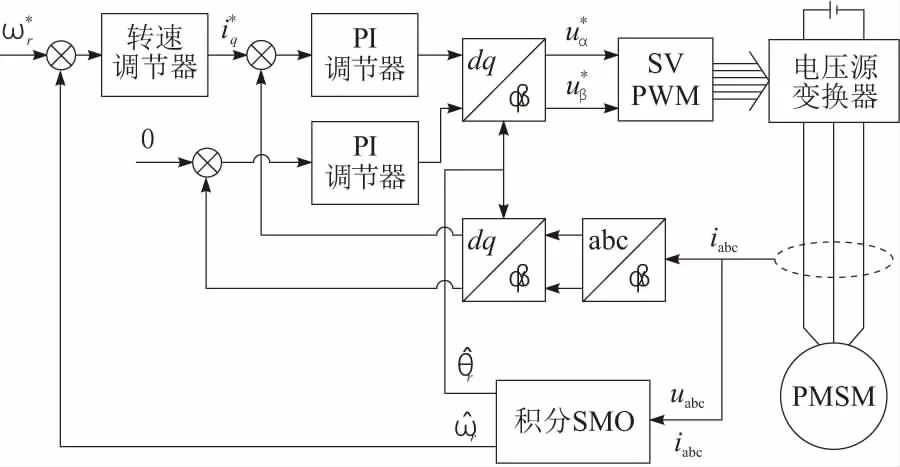
圖2 永磁同步電機控制模型
3 仿真驗證
搭建永磁同步電機仿真模型,將本文所設計的積分滑模觀測器同傳統滑模觀測器控制進行仿真對比,驗證本設計的有效性。
永磁同步電機參數如表1所示,控制器參數設置,由于電機調試最轉速為2 000 r/min,所以取滑模參數γ=110,K=110,c1=1.2,c2=0.3。

表1 PMSM參數
分別搭建傳統滑模觀測器和積分滑模觀測器進行永磁同步電機控制。電機運行時間設定為0.2 s,電機的起始轉速設定為n=1 000 r/min(在t=0 s時刻)。在電機運行到t=0.06 s時刻,轉速增加到n=2 000 r/min。在t=0.14 s時刻,電機突加TL=1 N·m負載轉矩。
圖3、圖5為永磁同步電機傳統滑模觀測器的仿真波形,圖4、圖6為永磁同步電機積分滑模觀測器的仿真波形。通過對比圖3和圖4可知,在電機由靜止到轉速為1 000 r/min階段(t=0 s時刻)和電機加速調節階段(t=0.06 s時刻),傳統滑模觀測器控制下,電機轉速具有較為明顯的超調量,且電機轉速持續大幅度波動,不能達到設定的轉速數值。在t=0.14 s時刻,電機出現較大負載擾動,使得電機轉速出現較大的跌落后,經過一段時間恢復到給定轉速附近,但電機轉速波動幅度仍然較大,不能準確控制在預期轉速上,波形如圖3所示。
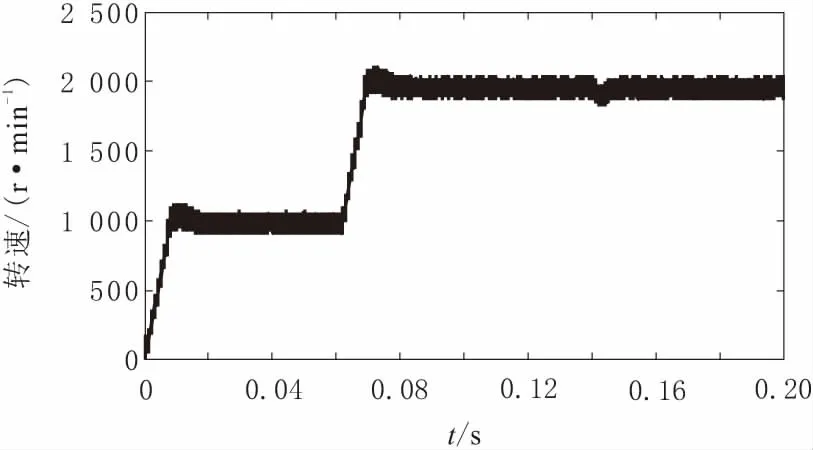
圖3 PMSM SMO轉速波形
在積分滑模觀測器控制中,積分滑模控制可以有效提高控制的精度和抑制滑模抖振現象,在電機起動(t=0 s)階段和加速(t=0.06 s)階段,轉速可以快速升高并達到預先設定轉速值,且轉速的超調量和穩態控制誤差均較小,當電機負載出現大幅擾動時,電機轉速有略微降落,在出現幾個震蕩周期的波動后迅速達到穩定值,表現出了優良的轉速控制性能和抗干擾能力,轉速波形如圖4所示。
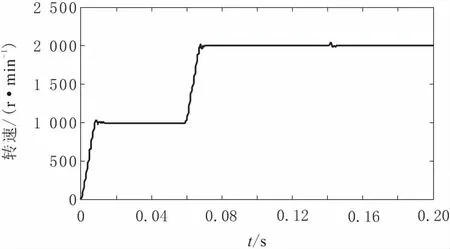
圖4 PMSM積分SMO轉速波形
通過對比傳統滑模觀測器控制和積分滑模觀測器控制相位檢測波形,積分滑模觀測器控制表現出了較優良的相位檢測特性,電機的相位檢測誤差更小更精確,對負載變化具有良好的適應性,為電機交直軸電流解耦提供良好保障。電機相位波形分別如圖5和圖6所示。
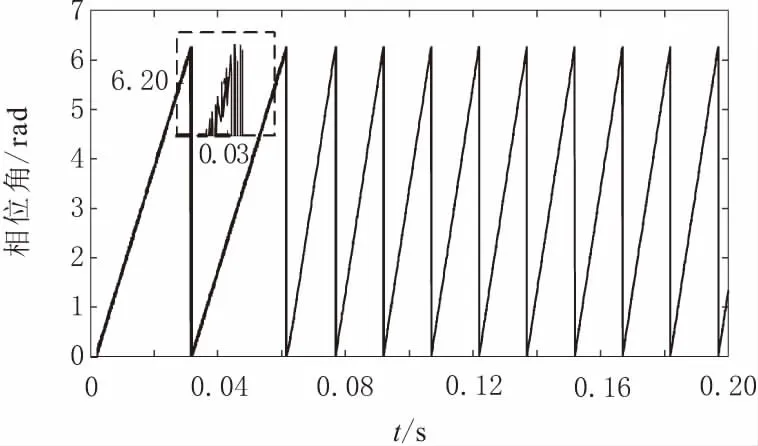
圖5 PMSM SMO相位波形
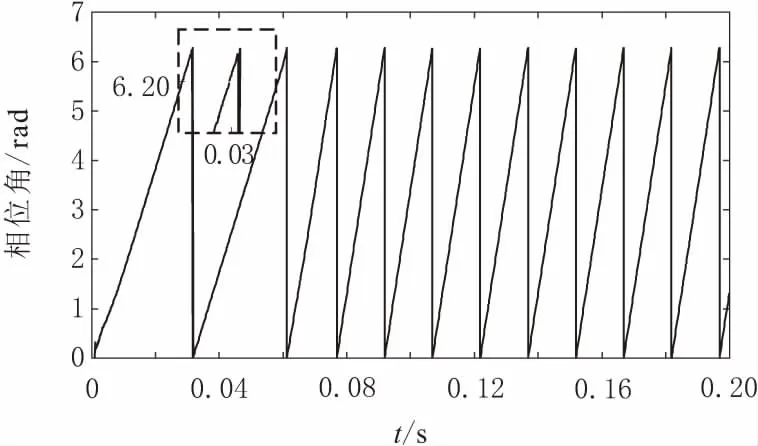
圖6 PMSM積分SMO相位波形
由仿真結果可知,基于積分滑模觀測器控制的永磁同步電機控制在抗干擾性能和轉速控制精度方面性能更優良。
4 結束語
實現永磁同步電機觀測器控制,提高觀測器控制精度和抗干擾能力,文章基于傳統滑模觀測器設計了一種積分滑模觀測器控制策略。設計積分滑模面,滑模觀測器趨近律采用指數趨近律。積分滑模控制有效抑制滑模抖振,提高滑模控制的精度,降低控制穩態誤差。為進一步抑制滑模控制抖振,通過設計飽和函數對滑模控制進行優化。通過搭建仿真模型進行控制有效性檢驗,證明了本文設計控制模型可以有效實現永磁同步電機觀測器控制。

