概率配點法在彈箭氣動不確定性分析中的應用
郭永翔
(中國兵器工業第203 研究所,陜西 西安710065)
1 概述
在CFD 模擬中,加工公差引起的幾何模型不確定、邊界條件及物性參數的不確定等不確定性因素也會對模擬結果有影響。為此,學者們開發了不確定性分析的非嵌入式方法。此方法可以利用經過確認的成熟的CFD 軟件,省去了對求解器的修改。概率配置點法(Probabilistic Collocation Method,PCM)就是非嵌入式方法中一種極具優勢的方法。
Loeven 等[1]發展了用拉格朗日插值多項式構造隨機變量的非嵌入式概率配點法,通過與嵌入式多項式混沌法及蒙特卡洛(Monte Carlo,MC)方法的對比,驗證了該方法的準確性和高效性,他們還對翼型NACA0012 進行了不確定性分析[2],包括來流速度的不確定和翼型幾何的不確定。Cinnella 等[3]將PCM應用于二維翼型NACA0012 跨音速流動的不確定性分析,并采用不確定性分析結果與基于多目標的遺傳算法相結合,對翼型進行了魯棒優化(robust optimization)。王曉東[4]采用概率配點法對NASA rotor37 進行了在出口壓力為不確定性條件下的魯棒優化。劉智益等[5]采用該方法模擬了風力機翼型的來流攻角作為正態分布的隨機變量的算例,研究了攻角不確定性對于翼型氣動性能的影響。
由加工裝配誤差等引起的彈箭幾何不確定性以及飛行過程中氣流速度的不確定性,彈箭的繞流場和氣動力載荷也具有一定的隨機不確定性。這些不確定性可能會使旋轉彈箭發生彈道失速、轉速閉鎖及災難性偏航等嚴重的后果。因此研究不確定性對彈箭氣動性能的影響是很有必要的。本文主要對標準模型BasicFinner 的來流不確定性對氣動參數及流場的影響進行了分析。
本文結構如下:第二節介紹了概率配點法,第三節對Basic Finner 模型的來流不確定性進行了模擬,第四節給出了結論。
2 概率配點法介紹
首先給出廣義隨機微分方程的形式,


3 不確定性分析結果
Basic Finner 外形由錐形頭部、圓柱形彈身和4 片十字布局的尾翼組成,外形尺寸見圖1,尺寸單位為彈徑。在風洞實驗和本文的數值計算中,彈徑的名義尺寸均為30 mm。
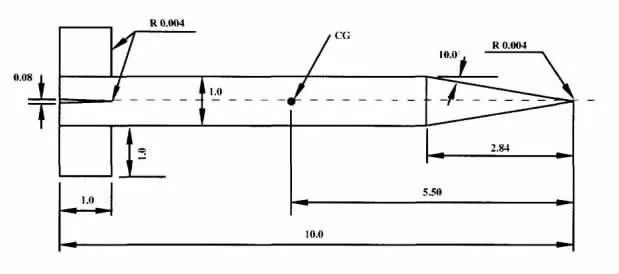
圖1 Basic Finner 外形
不確定性分析選取了馬赫數1.5,假定來流馬赫數為隨機變量。根據工程經驗,認為來流馬赫數為服從正態分布的隨機變量,馬赫數標準差為均值的0.5%。不確定性分析中,采用了二階配置點,配置點1 馬赫數為1.474,權重為0.1667;配置點1 馬赫數為1.5,權重為0.6667;配置點1 馬赫數為1.526,權重為0.1667。
圖2 是馬赫數不確定性下法向力系數統計均值及不確定帶與試驗值對比。如圖所示,馬赫數不確定性下的統計均值與試驗值吻合。法向力系數不確定帶隨攻角增大而變寬。

圖2 法向力系數均值與試驗值對比
圖3 為馬赫數不確定性引起的彈身截面及右翼截面壓力系數標準差云圖。如圖所示,彈身標準差的極大值區域出現在前緣脫體激波附近及尾翼脫體激波附近,此外頭部與彈身連接處的膨脹波區域也有較小的標準差;彈翼標準差極大值區域出現在在激波位置附近及膨脹波區域,激波附近的標準差更大。
4 結論
本文在不確定性CFD 模擬方法介紹的基礎上,研究分析了流動參數馬赫數為不確定變量時,Basic Finner 彈箭模型總體氣動參數和流場壓力系數的不確定性規律。結果表明,馬赫數不確定性引起的法向力系數變化量隨攻角增大而增大。流場內氣流參數梯度較大的地方(超聲速時尾翼前的脫體激波、尾翼背風面的膨脹波等處),馬赫數不確定性下的壓力系數變化,通常較其它區域大。概率配點法在彈箭氣動不確定性分析上具有精度高、計算速度快等優勢,可以用于之后的分析研究。
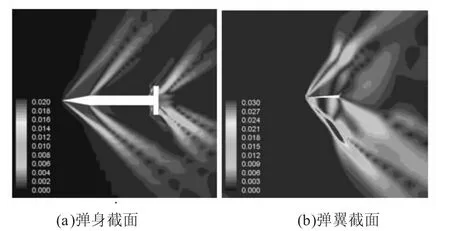
圖3 馬赫數不確定性流場標準差云圖

