一種提高連續波雷達目標檢測精度的方法

袁 濤， 葛俊祥， 鄭啟生

(1.南京信息工程大學江蘇省氣象探測與信息處理重點實驗室， 江蘇南京 210044；2.南京信息工程大學電子與信息工程學院， 江蘇南京 210044)

0 引言

線性調頻連續波(Linear Frequency Modulated Continuous Wave，LFMCW)雷達的發射信號在時間上是連續的，在頻率上是隨時間呈線性變化的。線性調頻連續波雷達具有距離分辨率高，測量范圍的盲區小，雷達發射的峰值功率低，具有低截獲特性等優點[1]。線性調頻連續波雷達通過對發射信號和回波信號混頻以后的差拍信號進行測量，從而提取目標的數據信息。線性調頻連續波雷達本身存在距離-速度耦合問題，對于單一的目標，對稱三角波雷達可以很好地解決這一問題，但是對于多運動目標就會遇到很多困難[2]，尤其當目標參數接近時。

對于進行頻譜細化處理的多目標檢測研究的資料較少。通常用FFT技術測量差拍頻率，由于FFT會帶來能量泄露和柵欄效應，從而使中心頻率的測量產生誤差[3]。所以進行多目標識別之前，要先對FFT之后的頻譜進行細化處理，能夠顯示出每個目標的頻譜，而且頻譜細化也減小對中心頻率測量的誤差[4]。本文應用CZT變換的方法進行頻譜細化，而且該方法也不會顯著地增加計算量。

針對頻譜配對問題，現在已有多種方法，如MTD-速度配對法[5-6]、面積法[7]、設計波形法[8-10]等。但是MTD-速度配對法計算量大，而且對具有相似反射強度和頻譜形狀的不同目標難以配對；面積近似的進行配對，該方法思想簡單，但是這種方法計算量也大；設計波形法，對對稱三角波進行設計，但是這種方法增加了信號處理的復雜度，在工程上應用較困難。當目標信息接近時應用上述方法無法區分出目標頻譜，不能完成頻譜配對。本文提出利用相關系數算法進行頻譜配對，該方法可以極大地減少雷達的誤檢率，計算較簡單，而且也方便在工程中應用。

1 線性調頻連續波雷達原理

LFMCW雷達發射的波形主要有鋸齒波和三角波。利用發射信號和接收信號混頻產生的差頻信號計算目標的速度和距離，其中三角波可以解決運動目標造成的多普勒頻移。

當目標是靜止時，目標與雷達有一定的距離R，回波信號與發射信號有一定的延時τ，兩者的關系為

τ=2R/c

(1)

式中，c為光速。

當目標是運動時，回波信號與發射信號之間會產生多普勒頻移fd：

fd=2v/λ

(2)

式中，v為目標運動速度，λ為波長。

由上下掃頻差拍信號計算出目標距離與速度的關系：

(3)

(4)

式中，μ為調頻斜率，f0為發射信號每個周期的初始頻率，fb,up和fb,down為上掃頻和下掃頻差拍信號頻率。

2 提高測量精度

設x(n)，0≤n≤N，它的z變換為

(5)

沿Z平面上的一段螺旋線作等分采樣，采樣點為Zk，

Zk=AW-k,k=0,1,2,…,M-1

(6)

式中,A=A0ejθ0,W=W0ejφ0，其中A0為起始采樣點的半徑長度，θ0為起始采樣點的相位角，φ0為每個采樣點之間的夾角，W0為螺旋線的伸展率。當W0>1時，螺旋線向內伸展，當W0<1時，螺旋線向外伸展，當W0=1時，表示半徑為A0的一段圓弧。

增加頻率的分辨率最直接的辦法可以增加采樣點數，但是增加采樣點數會使計算量增加，使用CZT變換可有效減少計算量，對測距測速最有關的是差拍信號的中心頻率，先用FFT粗略計算出中心頻率的位置k，在k的小范圍內進行CZT變換，計算出中心頻率的大小，再使用式(3)、式(4)計算出目標的距離和速度。

3 頻譜匹配

當同一方向上，一個天線波束能掃描到有m個目標時，上掃頻差拍信號和下掃頻差拍信號各計算出中心頻率m個，經過頻譜配對共有m2個結果，會產生m2-m個虛假結果，目標越多，虛假的結果也會越多，所以要運用簡單的方法，完成頻譜配對，計算出目標的距離和速度信息。

為了研究上掃頻差拍信號和下掃頻差拍信號頻譜的關系，假設x(f)為上掃頻中某個目標的差拍信號的頻譜函數，y(f)為下掃頻中某個目標的差拍信號的頻譜函數。

將上下掃頻差拍信號的頻譜離散化，對每一個峰值函數各提取n個數據，每n個數據為一個數組，共有2m個數組，對某個目標的上掃頻和下掃頻差拍信號頻譜函數計算相關系數。

函數的相關系數：

(7)

式中，cov(x,y)為上下掃頻兩個數組的協方差，σx為上掃頻數組的標準差，σy為下掃頻數組的標準差。

相關系數|ρx,y|≤1，若兩個信號的相關系數ρx,y=1，則表示兩個頻譜極度相似，認為是同一個目標產生的譜線。若相關系數ρx,y=0，則表示兩個頻譜不是同一個目標產生的，若相關系數 0<ρx,y<1，則表示兩個頻譜有一定的相似度，當相關系數ρx,y越接近1時，則兩個頻譜越相似，可以認為是同一個目標產生的。

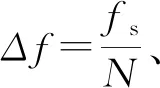
當同一方向上，一個天線波束掃描到多個目標時，通過雷達系統產生上掃頻和下掃頻差拍信號的頻譜。若第i個目標上掃頻差拍信號頻譜與每一下掃頻差拍信號頻譜的相關系數為ρi1ρi2…ρim，找出相關系數最大的認為是同一個目標產生的，完成頻譜配對。

4 算法實驗與數據分析

4.1 仿真實驗

仿真的雷達信號具體參數為：發射波形的中心頻率f0=85 GHz，調頻帶寬B=700 MHz,為了方便FFT和CZT計算，上下掃頻的周期都是T=1.024 ms，由調頻帶寬B和周期T計算出調頻斜率μ=B/T。

首先判斷目標的個數，如果只有一個目標時，上下掃頻差拍信號的頻譜可以直接配對，使用式(3)、式(4)計算出目標的距離和速度。

現在假設目標數m=4，目標的具體參數為：目標m1的距離R1=30 m，速度V1=20 m/s；目標m2的距離R2=30 m,速度V2=25 m/s；目標m3的距離R3=35 m,速度V3=20 m/s；目標m4的距離R4=35 m，速度V4=25 m/s。

圖1是上下掃頻時發射信號與回波信號混頻形成的差拍信號，并對差拍信號進行FFT的結果。運用現在的方法進行檢測目標，無法正確檢測出4個目標。由于兩個目標的速度接近，兩個目標的頻譜相互干擾，現在的配對方法會存在誤檢率。

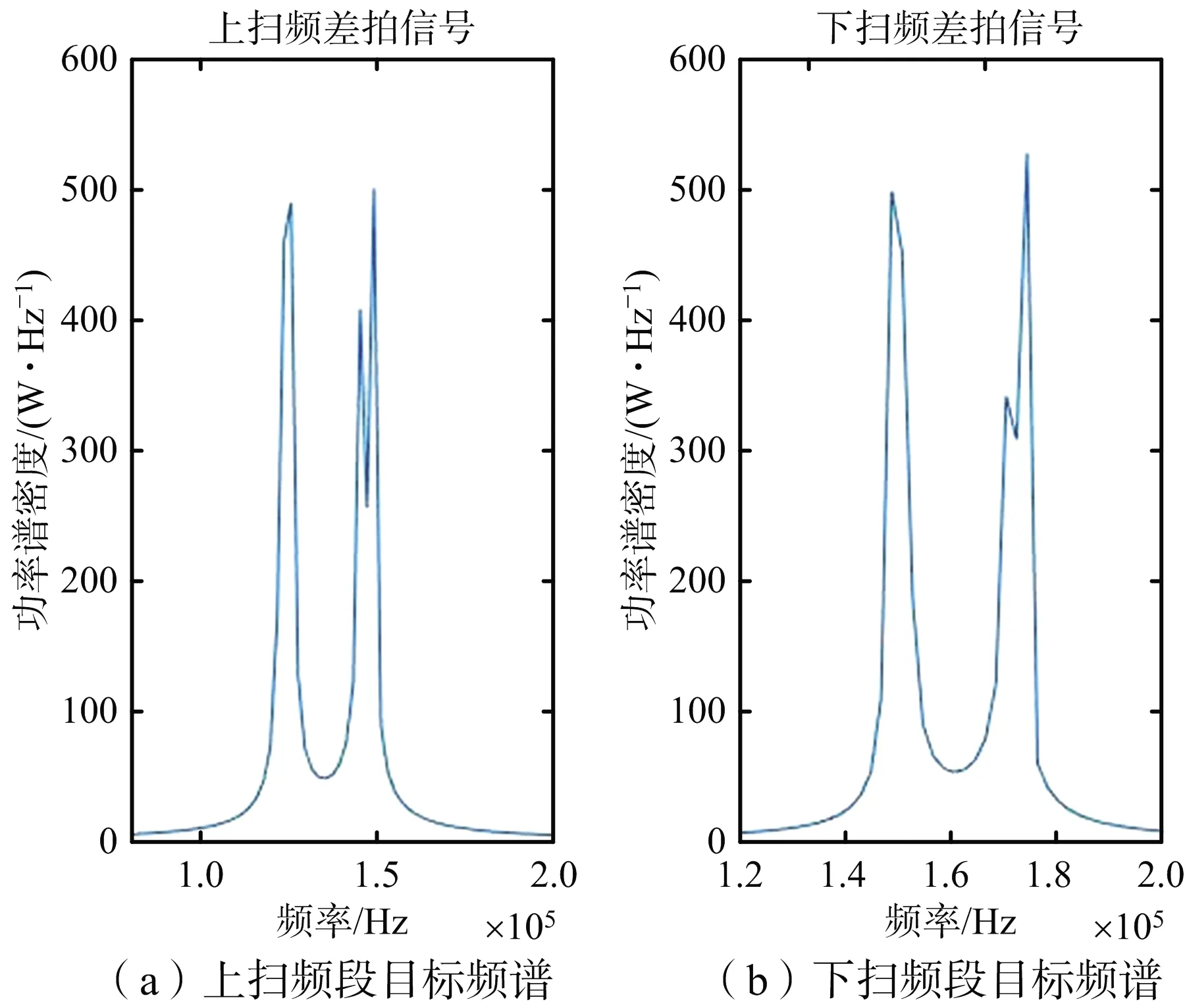
圖1 對差拍信號做FFT的仿真結果

圖2是使用FFT+CZT的方法對上下掃頻差拍信號進行分析。由圖可見，上下掃頻差拍信號的頻譜圖都有4個峰值，該方法成功地檢測出了4個目標。為了方便相關系數法進行頻譜配對，要對每個峰值函數進行標記。圖2(a)上掃頻差拍信號頻譜中頻率由小到大，峰值函數依次標記為A，B，C，D。圖2(b)下掃頻差拍信號的頻譜中頻率由小到大，峰值函數依次標記為a，b，c，d。

圖2 對差拍信號做FFT+CZT的仿真結果

對峰值函數進行頻譜配對，運用相關系數法，在上下掃頻差拍信號的頻譜中各取n個數進行計算。以峰值點為中心，而且只能在一個峰值函數內取值，根據以上原則這里取n=10，一共16個結果組成一個表格。根據相關系數最大數的原則進行配對。

相關系數配對的數據如表1所示，根據最大數原則，數據越接近1，兩個頻譜越相似，認為兩個頻譜是由同一個目標產生的。配對的結果為：A和b配對，B和a配對，C和d配對，D和c配對。

表1 上下掃頻差拍信號頻譜相關系數

由FFT+CZT+相關系數法解決了現在對兩個目標距離和速度信息接近時無法解決的問題。配對成功后計算出上下掃頻差拍信號的中心頻率fb,up和fb,down，根據式(3)、式(4)計算出目標的距離和速度信息。

表2是目標的測量距離和測量速度還有數據誤差分析，通過表2可以看出每一個測量的數據和實際數據的誤差都小于1%，因此CZT變換明顯地提高了測量的精度。

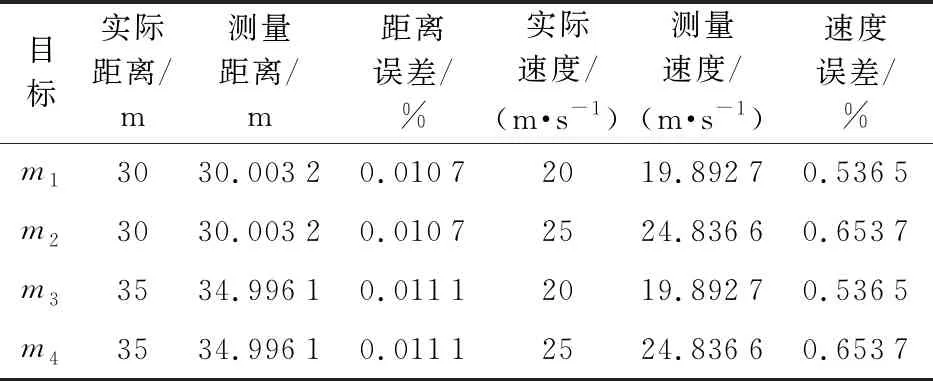
表2 目標的距離和速度誤差分析

4.2 數據分析

利用FFT對差拍信號進行分析時，采樣頻率為1 MHz，采樣點數為512，無法區分4個目標的頻譜。利用CZT對差拍信號分析時，采樣點數為1 024，頻率分辨率為49 Hz，明顯地區分了4個目標的頻譜。

FFT增加采樣點數也可以達到CZT的效果，但是計算量是CZT的幾倍。FFT和CZT頻率分辨率都是49 Hz時，計算量分別為20 480log220 480= 292 864，512log2512+2*(1 024+512)+(1 024+512)log2(1 024+512)=23 962，FFT的計算量約是CZT的12倍。可見CZT明顯地減少了計算量。

由于速度的分辨率受頻率分辨率的影響，如圖3所示給出了4個目標的CZT采樣點數與速度誤差的關系圖。增加采樣點數會減少速度的誤差，但是隨著采樣點數的增加計算量必然增加。由圖所示，隨著采樣點的增加，速度誤差基本趨于穩定，增加更多的采樣點，誤差變化不明顯。本文CZT采樣點為1 024。

(a) 目標1速度誤差變化

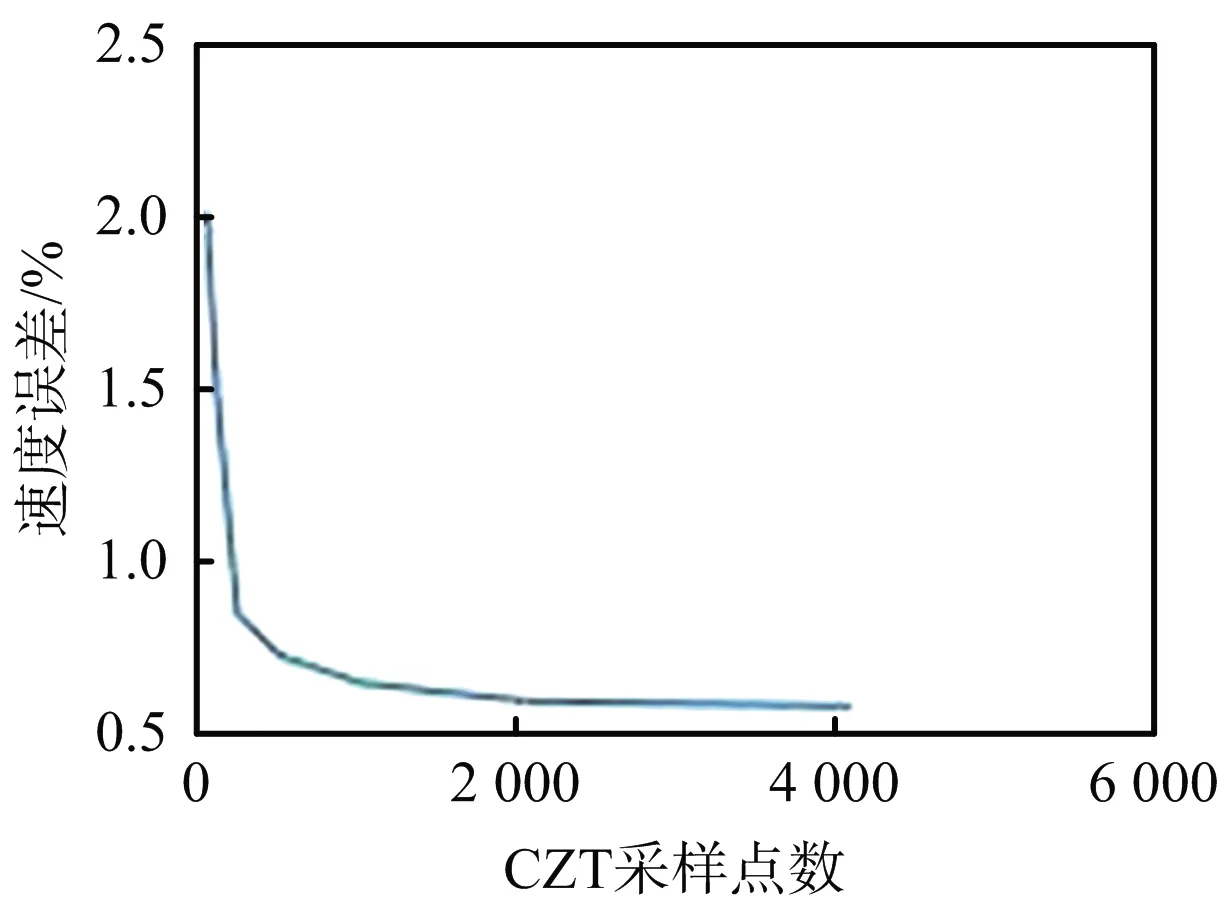
(b) 目標2速度誤差變化

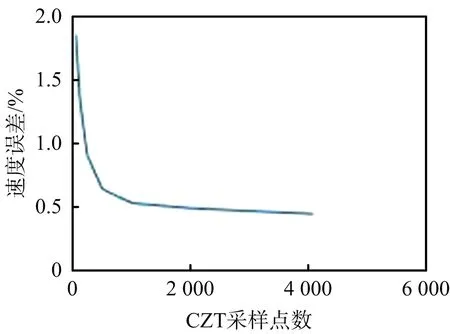
(c) 目標3速度誤差變化

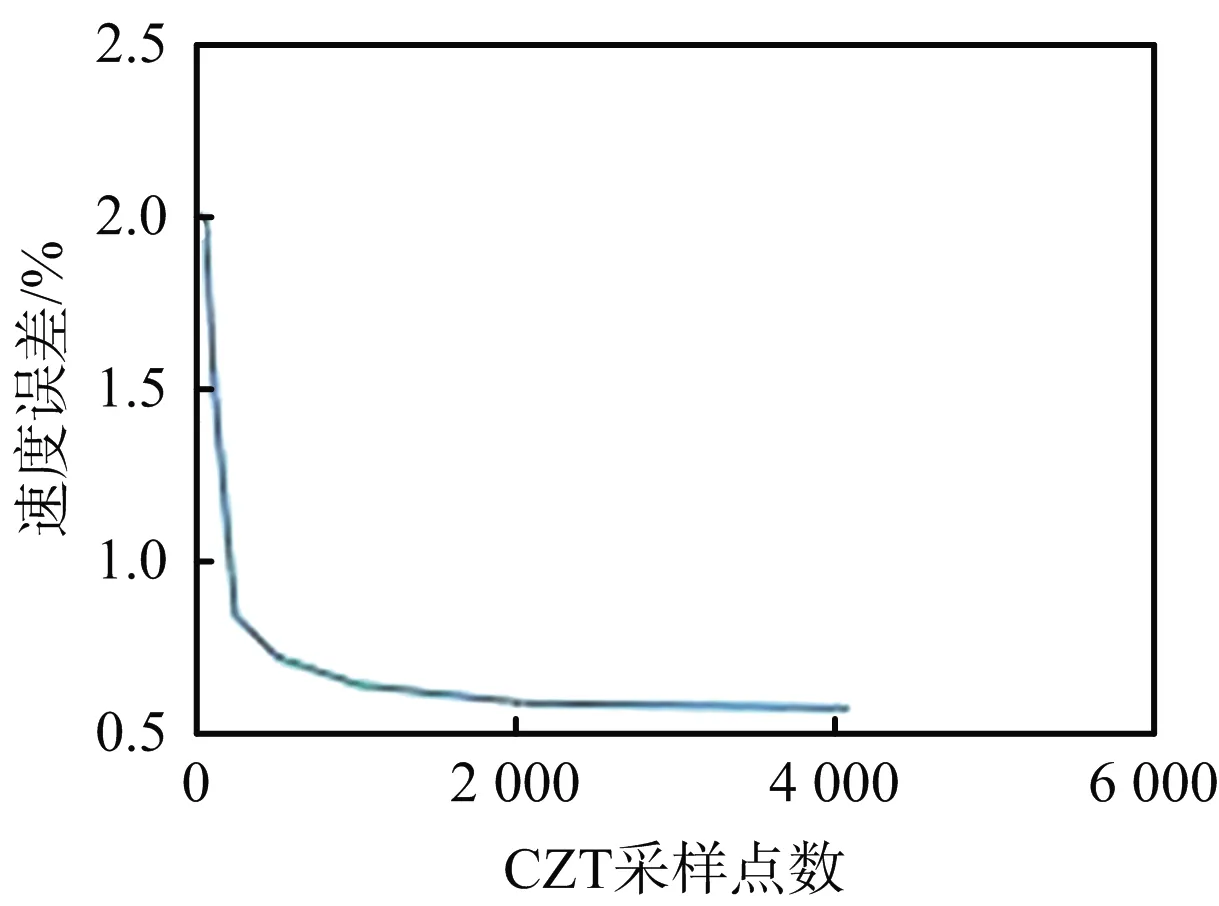
(d) 目標4速度誤差變化

對于配對方法，當目標參數相近時，以前的方法會有很高的誤檢率。如圖4所示，不能區分出每個目標差拍信號的頻譜，因此無法顯示出所有的配對結果。

圖4 FFT處理之后進行頻譜配對的結果

如圖5所示，對上下差拍信號頻譜細化后，再用相關系數法計算出了所有的配對結果，然后找出了4個真正的目標。誤檢率達到了0。

圖5 FFT+CZT處理之后進行頻譜配對的結果

5 結束語

針對多個動目標速度距離參數接近時，頻譜配對難的問題，本文提出了一種新型的FFT+CZT+相關系數的方法，有效地解決了這一問題，同時也提高了測量數據的精度。結合線性調頻三角波的特點，通過FFT鎖定上下掃頻差拍信號的中心頻率的位置，再通過CZT對頻譜進行細化處理，得到上下掃頻差拍信號的頻譜，應用相關系數法完成頻譜配對。相關系數配對法比現在的方法計算量小，更準確，該方法進行頻譜配對明顯地降低了誤檢率。然而該方法僅適用于同一方向、同一天線波束中的多目標檢測。下一步工作是拓展該方法應用在不同方向的多目標檢測。