基于非平穩信號組合分析的故障診斷方法

陳哲，胡玉其，田世慶，陸慧敏，徐立中

（1.河海大學計算機與信息學院，江蘇 南京 211100；2.日本九州工業大學機械智能工學研究系，北九州 804-8550）

1 引言

振動、溫度、壓力等非平穩信號產生于能量轉化過程中，普遍存在于工業生產各環節，對其分析和處理是工業過程控制、狀態估計、故障診斷等研究的課題之一[1]。對于此類信號，傳統分析方法多提取具有明確物理含義（如頻譜、時頻信息）的信號特征來表征設備狀態信息，常用方法包括時?頻域統計特征分析[2]、快速傅里葉變換[3]、小波變換[4]、時頻圖分析[5]、經驗模式分解[6]以及信號統計學特征[7]等。該類方法有利于構建運行狀態與原始信號間的因果耦合關系模型，受到了廣大研究者的推崇。然而，基于此類模型驅動的技術策略的不足之處在于特征表征的冗余度大、噪聲強、不同狀態特征間的類間差異性不足。為了解決這一問題，多種降維技術被應用于后續處理環節，常采用的方法包括主成分分析法[8]、獨立分量分析法[9]、流形學習[10]等，在一定程度上實現了冗余壓縮，但是仍難以提高特征的表征能力，影響故障診斷、狀態估計等應用的分類準確率。近年來，深度學習相關方法被應用于非平穩信號分析。不同于傳統基于模型的信號分析方法，深度學習通過大數據驅動的學習及多層樣本映射，能夠提取高度抽象化且具有極強表征能力的深度表達特征，具有優越的狀態辨識能力，深度置信網絡[11]、稀疏自編碼器[12]、去噪自編碼器[13]、卷積神經網絡[14-16]等模型被廣泛應用于非平穩信號分析。然而，大量的研究證明，該類學習方法的不足之處在于，所提取的深度表達特征缺乏明確的物理含義，難以有效解析信號屬性，特征性能常出現較大波動，穩定性和推廣性均難以適應。

現有頻譜、時頻分析或深度學習等多類非平穩信號分析方法各具特色，在信號特征的解析性、穩定性和準確性上難以權衡。考慮到非平穩信號頻譜、時頻和深度表達特征各自的優缺點和互補性，本文提出了一種非平穩信號組合分析方法，能夠并行提取信號的多類特征并加權融合。在以振動信號為例應用于故障診斷的實驗研究表明，所提信號組合分析方法具有較好的特征表征能力，在不顯著增加計算復雜度的前提下有效提高了故障診斷的準確性。同時，本文研究工作是對基于特征融合的故障診斷方法的一項探索。本文的主要創新和貢獻如下。

1) 特征提取。提出了一種雙流網絡架構，組合分析非平穩信號的頻譜、時頻及深度表達特征，以實現對信號的完整描述。

2) 特征融合。提出了基于壓縮?拼接?激勵（SCE，squeeze-connect-excitation）的雙流特征加權融合方法，以實現非平穩信號特征的統一表征。

3) 特征辨識。在故障診斷實驗中，所提組合分析方法能夠有效提高診斷準確性，有望滿足工業條件下的應用需求。

2 相關研究

故障診斷領域的非平穩信號分析及特征提取方法主要分為基于信號處理模型和基于深度學習的技術策略。

信號處理模型能夠清晰表征信號的物理屬性，如時變、頻譜和頻譜時變屬性等。例如，文獻[3]利用全局譜分析方法對非平穩振動信號進行分析，綜合采用包絡檢測方法與快速傅里葉變換方法進行信號預處理。文獻[4]使用小波變換和包絡譜分析，從非平穩信號中提取特征參量，并輸入故障診斷系統中進行故障分類。文獻[6]利用能量算子解調理論和經驗模態分解方法，對軸承非平穩振動信號的特征進行提取。文獻[7]提出了基于小波變換高階統計量的非平穩信號分析及滾動軸承故障診斷方法，該方法采用小波變換的四階統計量有效捕捉振動信號中的非平穩或奇異分量，以表征信號的奇異性。

深度學習方法能夠提取高度抽象化且具有極強表征能力的深度表達特征，在信號特征辨識和分類中展現了良好的性能。例如，文獻[11]借鑒深度置信網絡在處理高維、非線性數據方面的性能優勢，提出一種基于深度置信網絡的信號分析及故障診斷方法，利用原始時域信號訓練深度置信網絡并完成智能診斷。文獻[12]提出了一種基于深度遷移學習的故障診斷方法，采用三層稀疏自編碼器對原始信號直接提取特征，應用最大差分項最小化訓練數據和測試數據特征之間的差異懲罰。文獻[14]提出了基于一維卷積神經網絡的信號分析方法，將電機故障檢測的特征提取和分類合并到單一的學習體中，有效提高了診斷效率。文獻[16]直接將原始振動信號輸入一維卷積神經網絡進行訓練，并通過自適應批量正則化計算提高變負載能力。

此外，部分研究還探索了基于級聯模型的信號分析方法。例如，文獻[17]將傅里葉變換與卷積神經網絡模型結合，用于提取非平穩信號特征。文獻[18]將多信號特征輸入卷積神經網絡模型，提取深度表達特征，由于多級映射過程，此類級聯信號分析方法所獲信號特征難以準確解析原始信號屬性，且常出現“過擬合”的問題。

3 非平穩信號組合分析

如圖 1 所示，本文所提出的非平穩信號組合分析方法采用雙流網絡框架，主要包括2 個分支流：上分支信號處理流主要完成傅里葉變換和小波包分解，用于頻域和時頻域的信號分析；下分支深度學習流由級聯卷積神經網絡（CB-CNN，cascade block convolutional neural network）組成，通過大數據驅動的多級映射過程提取深度表達特征。在多流特征融合中，本文提出基于SCE 模塊的特征加權融合方法。此外，為了適應故障診斷應用的需要，后端分類器采用2 個全連接層和一個Softmax 計算層相組合的精簡設計方案。

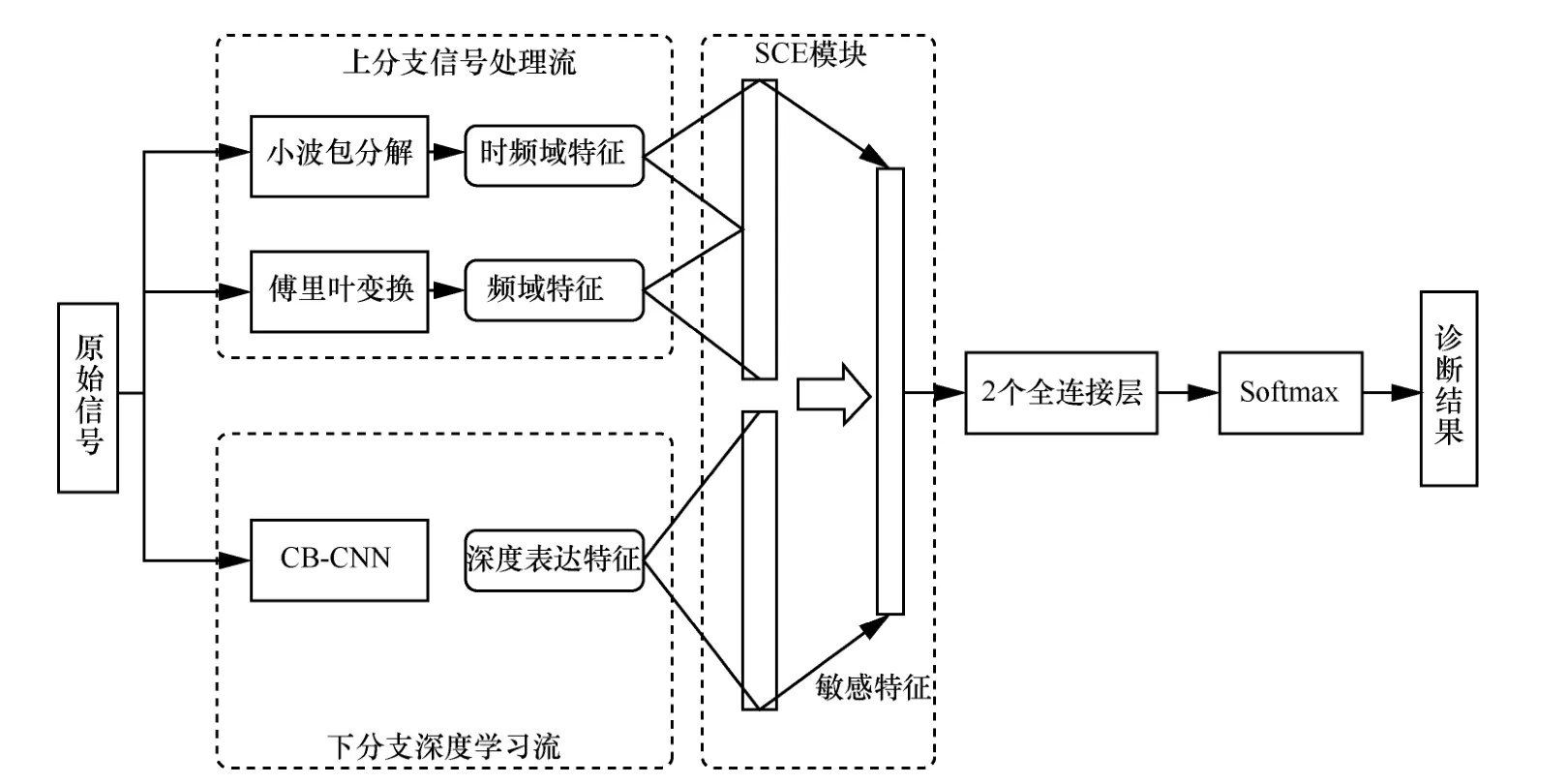
圖1 非平穩信號組合分析方法框架

信息間互補性是信號組合分析可行性和合理性的基礎，本文所提出的雙流信號組合分析方法所提取的特征間具有明確的互補關系。在上分支，基于傅里葉變換的頻譜特征能夠體現信號頻譜包絡的全局變化特性，而小波包分解后所提取的時頻特征能夠體現頻譜隨時間變化的局部特征，二者間的融合能夠從全局和局部細節上綜合反映信號的頻域特性。在下分支，CB-CNN 能夠通過多層映射挖掘原始信號抽象化的深度表達特征，同頻域和時頻域特征具有明確的互補性。此外，本文的雙流結構也可解釋為一種聯合模型驅動和數據驅動策略的并行組合分析方法，不同于以往級聯式多級處理策略，本文方法能夠更好地保存2 類特征本質特性并實現2 種模型的優勢互補。

4 基于雙流框架的特征提取

4.1 上分支信號處理流

4.1.1 小波包分解

本文采用小波包分解提取非平穩信號中的時頻域特征[19]，同時對低、高頻成分進行分解，以反映原始振動信號隨時間變化的局部頻譜特性，小波包分解過程如圖2 所示。圖2 中的A 和D 分別表示低頻系數和高頻系數，字母后的數字表示分解的層數。在此，本文選擇三層小波包分解架構，共得到8 個子頻帶，用表示為每個子頻帶的重構信號，每個子頻帶的能量可表示為

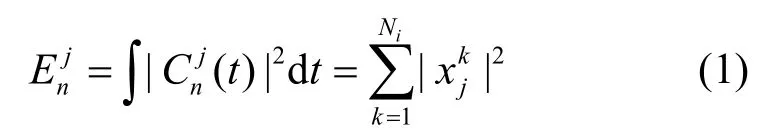
其中，n=3，j=0,1,…,7，Ni為重構信號的長度，為第j個重構信號的幅值。信號的能量均方根值可表示為

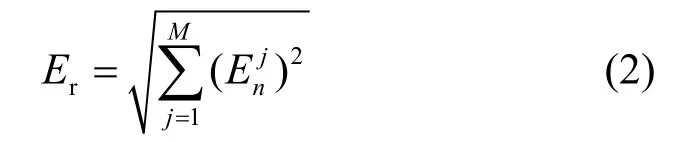
信號的能量譜特征可表示為

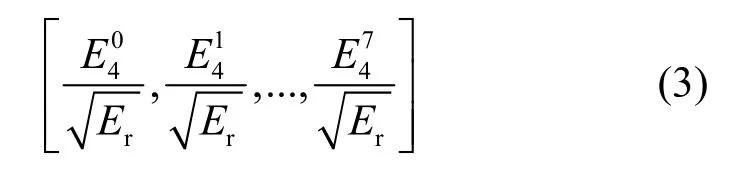
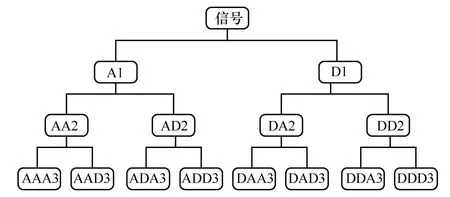
圖2 小波包分解過程

4.1.2 傅里葉變換

本文采用傅里葉變換提取信號中的頻譜特征。不同于時頻域特征，頻譜特征能夠表征非平穩信號的全局頻譜變化特性。對于離散的振動信號x(n)，其離散傅里葉變換可表示為

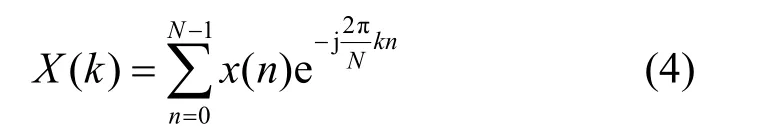
其中，k=0,1,…,N?1，N為離散序列的長度。

4.2 下分支深度學習流

本文所提雙流組合分析框架的下分支由CB-CNN 構成，用于提取高度抽象化的深度表達特征。區別于上分支所提取的頻譜和時頻域特征，該類特征無明確的物理含義且難以解析。但得益于大數據驅動的學習過程，深度表達特征表征同設備狀態間常具有強耦合相關性，有助于提高分析準確性。

下分支CB-CNN 整體架構如圖3 所示。在第一層卷積計算中采用了64×1 的大尺度卷積核，通過增大感受野以更好地保存原始非平穩信號的空間及時間相關性。通過第一層卷積后經過正則化、激活層及最大池化層處理，輸入后續兩級級聯塊。

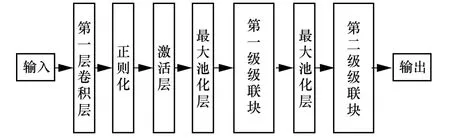
圖3 CB-CNN 整體架構

級聯塊的詳細結構如圖4 所示。

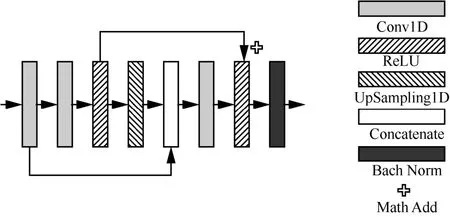
圖4 級聯塊的詳細結構

考慮到非平穩信號具有強時間相關性，會隨著級聯深度的增加而逐漸降低，不利于信號屬性的準確表征。針對這一問題，本文設計了2 條橋接支路以保存淺層特征中的時間相關性。該級聯模塊由八層操作組成，包括三層卷積、兩層ReLU、一層批量歸一化、一層上采樣和一層Concatenate 計算。其中，第一條橋接支路通過Concatenate 計算將第一層卷積結果與上采樣層的輸出進行連接；第二條橋接支路將前2 個激活層的輸出進行融合，實現淺層特征信息傳遞。

4.3 基于SCE 模塊的特征融合加權

在特征融合中，考慮到不同特征在表征性能上的差異，本文提出了一種基于SCE 模塊的特征融合加權方法，如圖5 所示。

SCE 模塊包含 2 個輸入，分別為下分支CB-CNN 深度學習流提取的維度為L×C1的特征矩陣和上分支信號處理流提取的1×C2的一維特征向量。本文中SCE 模塊的主要流程包括 Squeeze、Connect、Extraction 和 Reweight。

1) Squeeze。采用全局平均池化操作對特征矩陣X進行壓縮，以通過一維特征向量m代表二維特征矩陣X，獲得全局感受野。

2) Connect。經過Squeeze 計算得到雙流一維特征，采用Concatenate 操作實現多特征拼接。

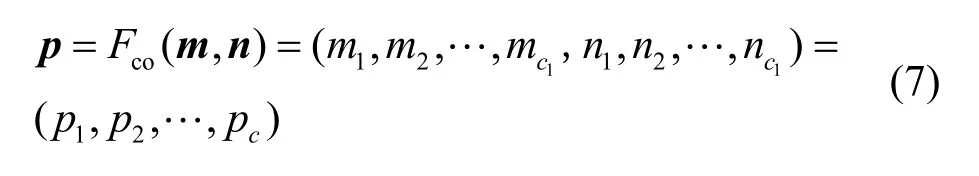
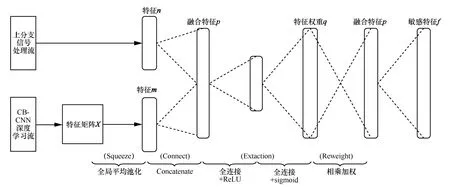
圖5 SCE 模塊

其中，C=C1+C2。

3) Excitation。主要通過多層次的特征降維估計特征權重q。

其中，W1和W2為學習得到的映射矩陣，δ和g為學習得到的映射函數。

4) Reweight。對特征進行加權運算，敏感特征f為

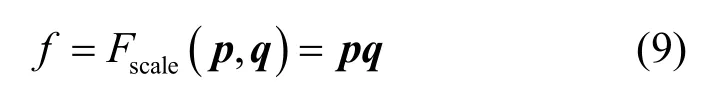
4.4 訓練策略

對于所提的雙流網絡架構，本文設計了一種分級訓練策略。考慮到上分支信號處理流采用基于模型的特征提取方法，訓練過程僅需要對下分支深度學習網絡參數進行優化。此時，若采用整體一次性訓練的技術方案會顯著增加無效的訓練計算。為了解決這一問題，在第一級訓練過程中對下分支的CB-CNN 進行單獨訓練，以生成預訓練模型。第二級訓練時，上下分支組合成完整網絡，繼續微調網絡模型參數，最終實現網絡整體優化。

5 故障診斷應用及實驗分析

5.1 實驗數據集

為了客觀評價本文所提出的信號組合分析方法的性能，在故障診斷實驗中進行驗證和分析，采用凱斯西儲大學軸承數據中心的數據集進行故障診斷實驗。凱斯西儲大學軸承數據中心的軸承系統平臺包括3 個負載電機（1hp、2hp 和 3hp）、一個扭矩傳感器和一個功率計。振動信號由加速度計以12 kHz 的采樣頻率采集。該數據集一共包括10 種軸承狀態，分別為正常狀態和9 種故障狀態。故障狀態包括內圈、外圈和滾動件上尺寸分別為0.007、0.014、0.021 的單點故障。對于每個負載電機，每個狀態隨機抽取1 000 個樣本，共10 000 個樣本，其中網絡訓練集樣本為7 000 個，驗證集樣本為2 000個，測試集樣本為1 000 個。

由于傅里葉變換和小波包分解特征具有不同的尺度，首先需要采用L2 范數歸一化方法對頻譜特征和時頻特征進行歸一化計算[20]，如式(10)所示。

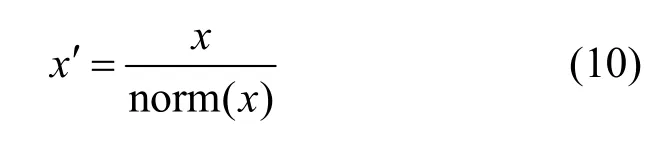
5.2 參數選擇和設計

本文雙流網絡架構主要層級的設計和參數選擇如表1 所示。

表1 雙流網絡架構主要層級設計和參數選擇

對于小波包分解，分解層數決定了時頻分析的分辨率和特征的維數。本文實驗首先對分解層數的選擇進行優化。不同層數下小波包分解特征的分類準確率如表2 所示。從表2 中可以看到，當進行三層小波包分解時，分類準確率最高。

表2 不同層數下小波包分解特征的分類準確率

5.3 訓練與微調

為了防止模型的“過擬合”和“欠學習”問題，首先對模型的收斂性進行實驗驗證。在本節實驗中，設置訓練階段的學習率為0.01，參數微調為0.005。圖6 和圖7 分別為訓練集和驗證集的準確率曲線及損失函數曲線。可以看出，當迭代次數為10時，模型達到收斂。

圖8 為測試集的混淆矩陣。其中，測試集共有1 000 個樣本，共10 種狀態，每個狀態分別對應100個樣本。從對測試集的分類結果來看，本文方法對于故障檢測的結果較好，僅一例RE0.014 樣本誤判為RE0.021 狀態。

5.4 與其他方法對比分析

5.4.1 準確率對比分析

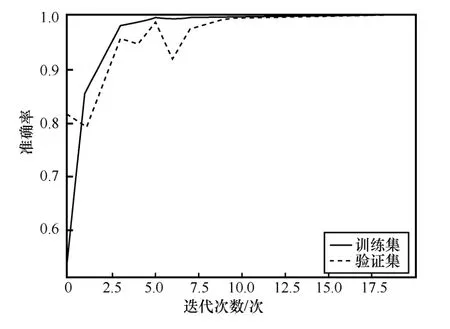
圖6 訓練集和驗證集準確率曲線

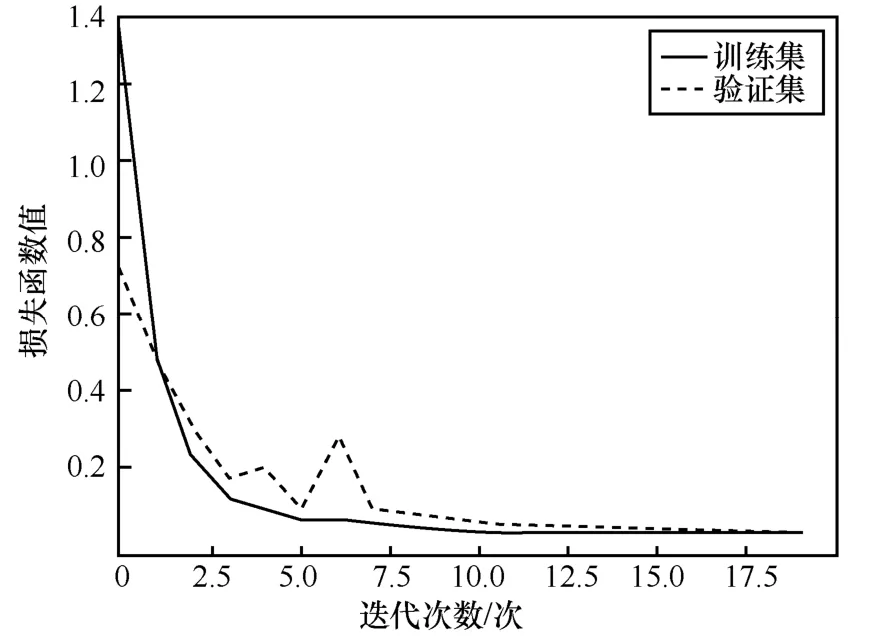
圖7 訓練集和驗證集損失函數曲線

圖8 測試集混淆矩陣

許多研究表明，基于深度學習的故障診斷方法在特征表征和分類正確性方面優于傳統方法[21-25]。但是，深度學習網絡極易陷入過擬合狀態，雖然對于個別案例獲得了極高的分類準確率，但仍難以取得較高的穩定性和推廣性。鑒于此，本節綜合選擇經典的深度學習模型和淺層模型作為實驗對比方法，包括SAE（stacked auto encoder）[21]、SDAE（stacked denoising auto encoder）[23]深度學習模型和Bayes[24]、支持向量機（SVM,support vector machine）[25]方法。圖9 展示了10 個非冗余測試數據集上本文方法和不同經典方法的分類率，表3 為本文方法和不同經典方法的平均分類準確率對比。

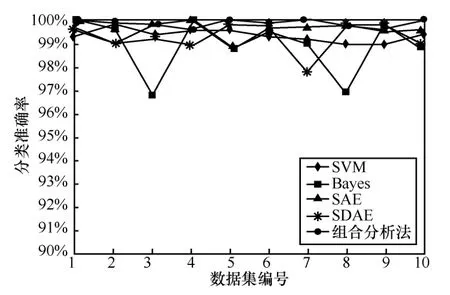
圖9 本文方法和不同經典方法的分類準確率

表3 本文方法和不同經典方法的平均分類準確率對比

綜合分析圖9 和表3 可知，本文方法明顯優于傳統方法，其分類準確率始終保持在99%以上。此外，SDAE 和Bayes 方法的分類準確率波動較為明顯，本文方法的分類準確率穩定維持在較高水平。

為了進一步評估本文方法，選擇近年來已證明較優越的深度學習方法作為對比，主要包括單分支的網絡模型WDCNN[16]（deep convolutional neural network with wide first-layer kernel）和PCNN[26]（physics-based convolutional neural network），以及多分支模型MSCNN[27]（multiscale convolutional neural network ）、MC-CNN[28]（multi-scale cascade convolutional neural network）和MDI-CNN[18]（multi-dimension input convolutional neural network）。圖10 展示了在10 個非冗余測試數據集上的本文方法和不同先進診斷方法的分類準確率，表4 為本文方法和不同先進診斷方法的平均測試分類率對比。

綜合圖9、圖10、表3、表4 的結果可以看出，與其他信號分析方法相比，本文方法獲得了最高的故障診斷分類率，對不同測試數據集的平均準確率達到99.85%。此外，提高網絡深度是一種較為常用的提高特征表征能力的技術策略，然而，增加網絡的深度常會導致過擬合問題。不同于這類技術策略，本文所提信號組合分析方法通過特征融合實現多流特征信息的互補及加權融合。與盲目地增加網絡深度相比，該策略在準確性和穩定性上具有更好的表現。此外，本文方法在故障診斷中的平均測試時間為4.102 ms，實現了較高的計算效率。

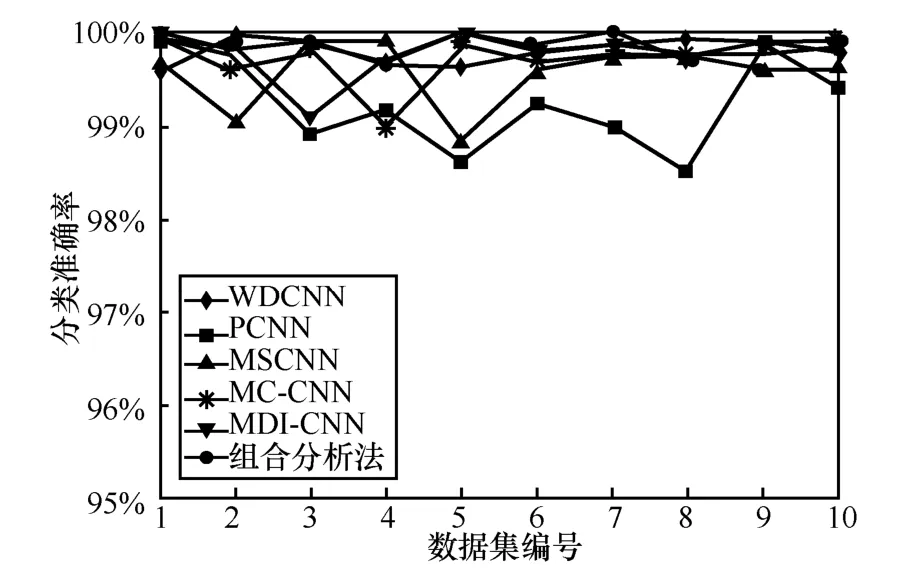
圖10 本文方法和不同先進診斷方法的平均分類準確率對比

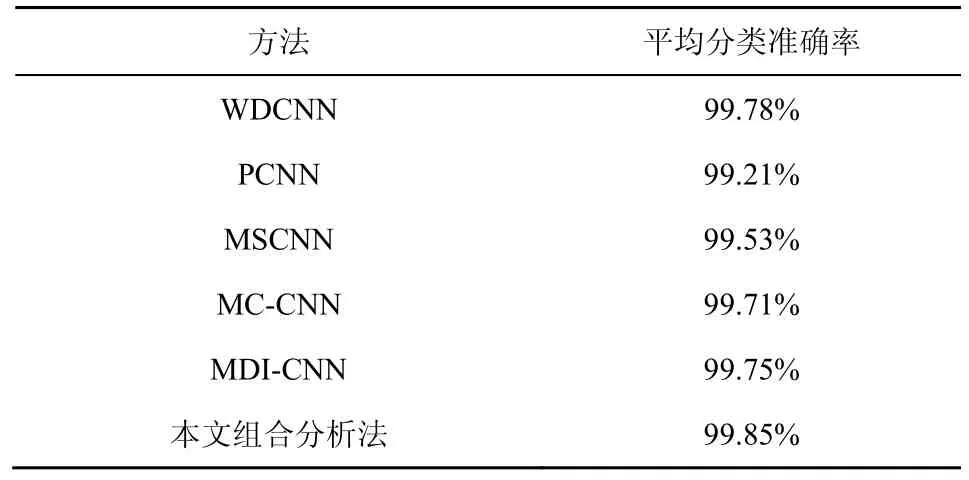
表4 本文方法和不同先進診斷方法的平均分類準確率對比

5.4.2 變噪聲條件下的對比分析

為了驗證本文信號組合分析方法的在不同噪聲條件下適應性，本節驗證其在信噪比（SNR,signal noise ratio）為?4～10 dB 條件下的分類準確率。表5 為本文方法與不同先進診斷方法抗噪性對比。可以看出，本文方法在不同信噪比條件下都獲得了較高的分類準確率，僅在SNR=4 dB 時，分類準確率略低于MDI-CNN 模型。

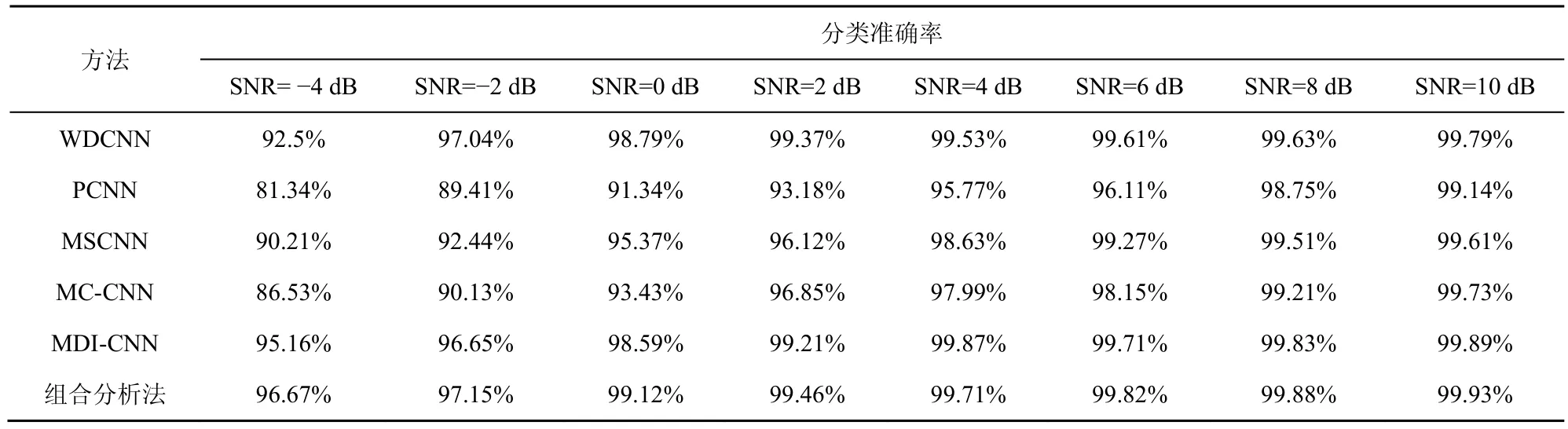
表5 本文方法與不同先進診斷方法抗噪性對比

5.4.3 變負載條件下的對比分析

在工業生產過程，儀器設備常出現負載變化，傳感器信號隨之變化，波動周期與相位差別顯著，會嚴重降低特征的穩定性。

跨負載條件下的故障診斷實驗（使用某一負載條件下的模型診斷另一負載條件下的故障）能夠有效展示不同信號分析及故障診斷方法的穩健性和推廣性。鑒于此，本文分別使用負載為 1 hp、2 hp與 3 hp 下的振動信號對雙流網絡模型進行訓練，使用其他2 種負載條件下的信號作為測試集進行測試。表6 為變負載測試模式，圖11 為本文方法與不同先進診斷方法的變負載能力對比，表7 為不同方法在不同模式下的分類準確率。

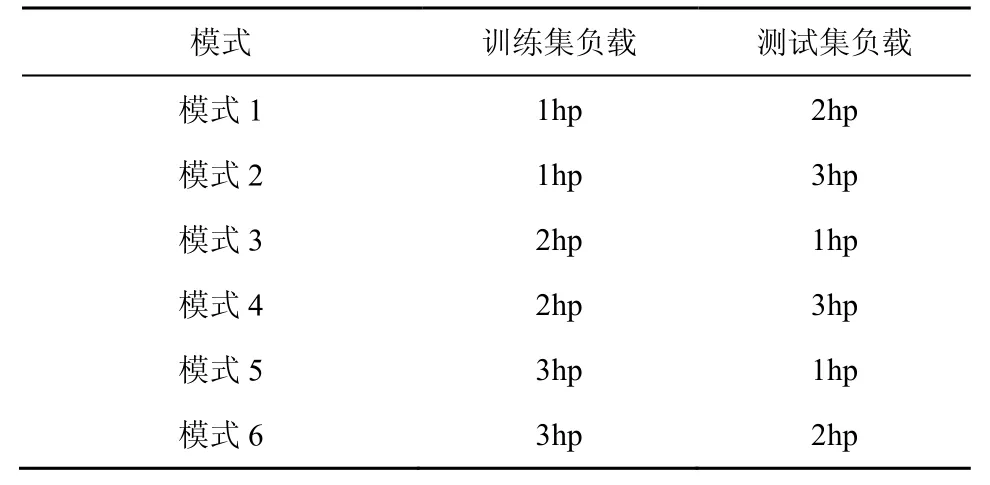
表6 變負載測試模式

從圖11 和表7 中可以看到，本文方法在6 種變負載模式下均獲得了較高的分類準確率，僅在模式5 下，準確率低于MDI-CNN 模型，證明了本文方法具有較好的穩健性和推廣性。

6 結束語

本文提出了一種非平穩信號組合分析方法，能夠綜合提取頻譜、時頻及深度表達特征并融合，以提高對非平穩信號的表征能力。應用于故障診斷實驗比較可以看到，本文所提方法能夠實現較為準確和穩健的故障診斷。

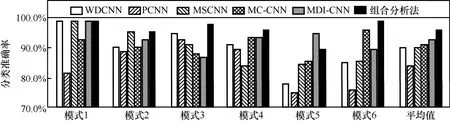
圖11 本文方法與不同先進診斷方法的變負載能力對比

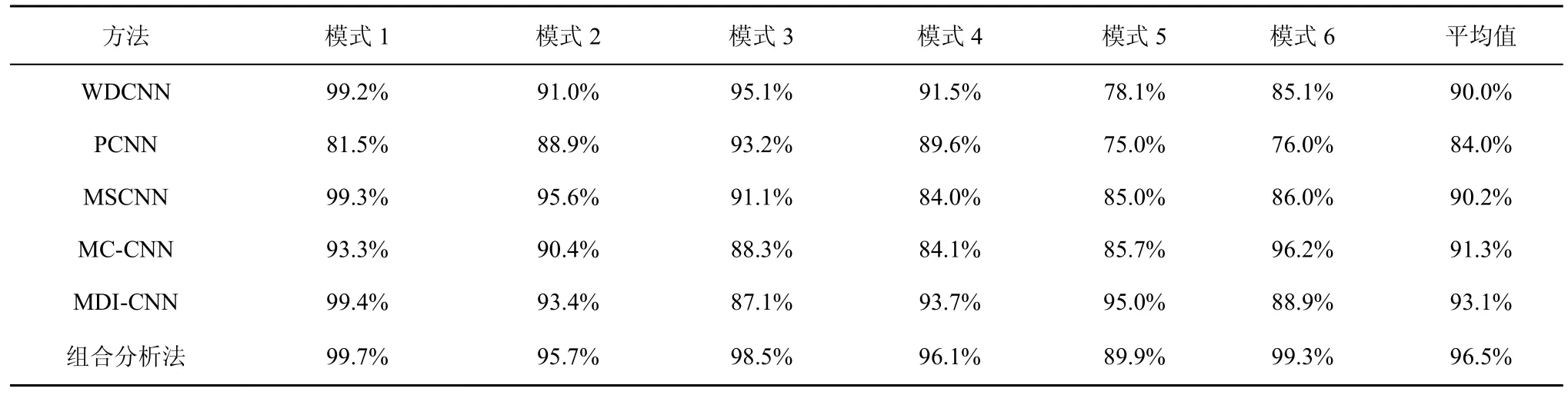
表7 不同方法在不同模式下的分類準確率

目前，多類深度學習方法在信號分析上表現出較為出色的性能，但其本質上采用完全基于數據驅動的技術策略，在實際應用中極易陷入過擬合狀態，即使對于個案取得了極為優良的結果，但在方法的穩定性和推廣性上仍值得商榷。此外，深度學習模型所提取的抽象化特征難以得到很好的解析，從而對未來的改進發展造成困難。與之相比，傳統的信號處理方法可以提取具有物理意義的特征，這對于信號分析結果的進一步解析和研究發展尤為重要。對于故障診斷應用，多類特征間的有機融合能夠有效提高診斷的準確性及穩定性，這將是未來本領域的主要發展方向之一。