基于支持向量機的油滴識別及粒徑分布特征提取算法

曹金鳳，郭繼鴻，李建偉，蘇天赟

(1.青島理工大學 a.機械與汽車工程學院；b.土木工程學院，山東 青島 266520；2.中海油能源發展股份有限公司安全環保分公司，天津 300450；3.自然資源部第一海洋研究所，山東 青島 266061)

海洋溢油事故是導致海洋環境污染的重要因素之一，也會對海洋生態系統造成嚴重且不可逆的影響。溢油從井口噴射進入海水后將以射流的形式運動，油滴粒徑的分布特征決定了油滴的總體運動狀態，從而影響溢油是否會上浮到海水表面或是在水體中分散[1]。海底條件復雜多樣，亟須考察多種工況下(諸如不同溫度、噴射口直徑等)油滴粒徑分布。

許多學者通過室內水槽實驗，實現對油滴流速、溫度、噴射口直徑等多種狀態的準確控制，從而模擬多工況下的油滴運動[2-6]。在水槽實驗中，需要人工標定和篩選實驗圖片中的油滴區域，較為繁瑣和不便，適用于試驗規模較小且試驗條件有限的情況，對大量試驗圖片進行快速準確的識別和篩選，難度較大且效率較低。

機器學習由于能夠從大量數據中學習，從而獲得數據的關鍵特征，因此，被廣泛應用于圖像識別領域。有學者開展了相關研究[7-11]。

為了實現對大量油滴圖片快速準確識別，本文提出了一種基于支持向量機(SVM)的油滴識別和粒徑分布特征提取算法。為了驗證該算法處理實際圖片的可行性，選用圖片均來自通過工業相機拍攝的室內水槽溢油噴射實驗圖片，并將識別結果與經典粒徑分布模型Rosin-Rammler模型對比。實驗結果表明，該算法能夠快速識別油滴圖片，并統計油滴的粒徑分布，為海底溢油應急搶險提供了理論基礎。

1 實驗過程

1.1 實驗裝置

研究選取的水下溢油模擬實驗水槽裝置見圖1、2，由水槽槽體、注油系統和控制柜構成；注油系統管路見圖3。水槽高2 m、底面尺度1 m×1 m，工作水深1.8 m。整個實驗過程采用工業計算機控制，輸油齒輪泵由變頻器控制，可人工調節管路中油樣的流量。

圖1 實驗室水下溢油模擬實驗水槽

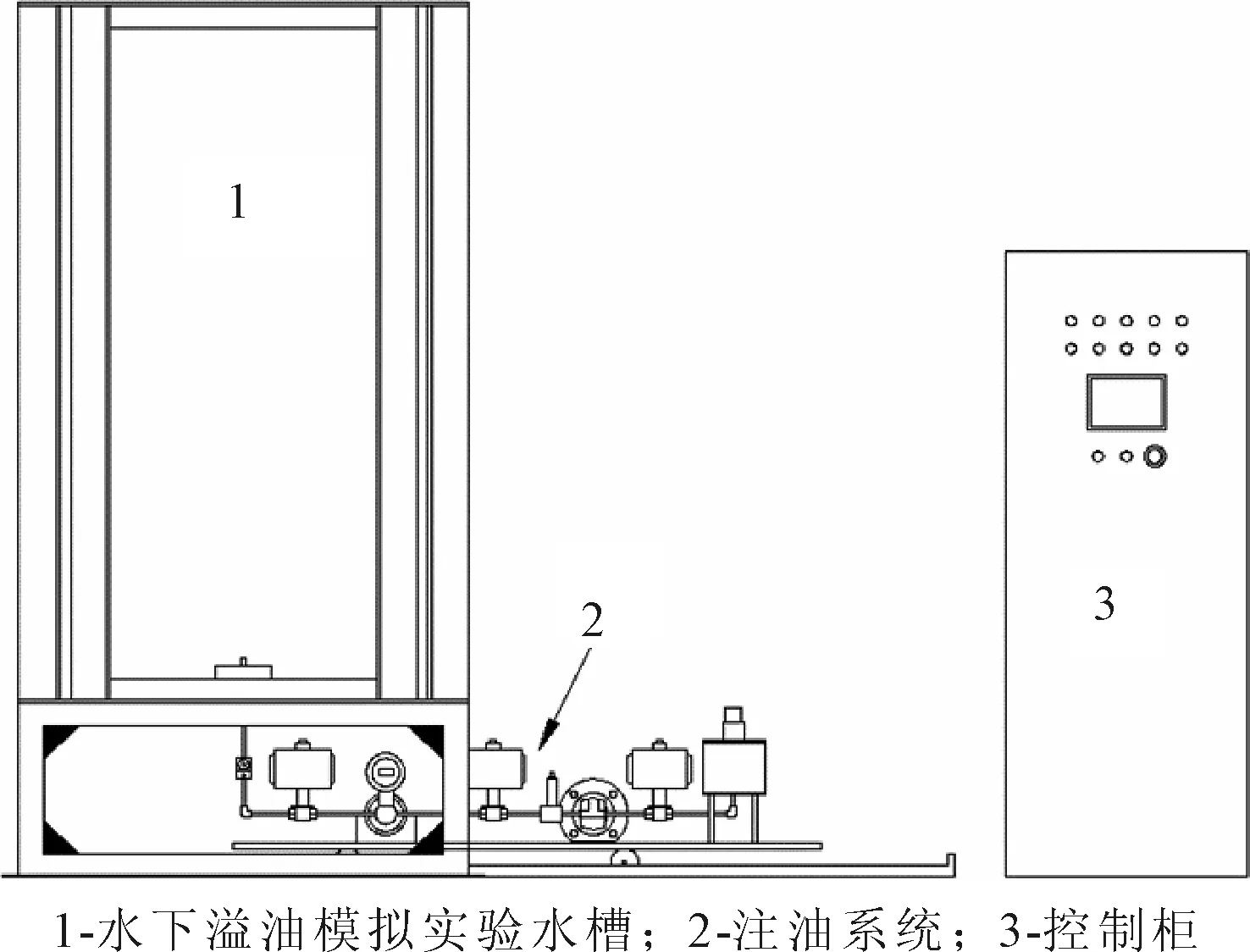
圖2 實驗水槽

1.2 實驗材料

研究過程中使用的原油油樣和天然海水的物理性質分別見表1、2。

表1 原油油樣物理性質

注：ρ-密度，kg/m3；μ-運動黏度，mm2/s；t-溫度，℃。

表2 天然海水的性質

1.3 實驗圖片采集

用2臺工業相機分別拍攝含較大油滴和較小油滴的溢油圖片。測定較大油滴粒徑的相機幀速率50幀/s，分辨率為200萬像素(2 048像素×1 088像素)，感光芯片名稱CMV2000，鏡頭分辨率200 μm。該相機掛于水槽外，相機鏡頭中心離噴嘴豎直距離為1.5 m。實驗前，應用有機玻璃直尺(最小刻度1 mm)對測試區進行了尺度標定。測定較小油滴粒徑的相機幀速率17幀/s，分辨率500萬像素(2 456像素×2 058像素)，感光芯片名稱ICX625，鏡頭分辨率5.8 μm。該相機掛于水槽內，相機鏡頭中心離噴嘴豎直距離為1.5 m。實驗前，應用顯微鏡C4測微尺(最小刻度50 μm)對測試區進行了尺度標定。

2 油滴圖片獲取及分割

對實驗圖片處理包括濾波和分割2個部分，處理流程見圖4。

圖4 對油滴圖片進行處理和分割的工作流程

2.1 圖像濾波

獲取的原始圖片背景中含有大量噪聲，背景噪聲的存在將直接影響最終的分割效果,因此,需要對圖片進行濾波處理，減少噪聲對于分割圖片的干擾。

濾波圖像的灰度均值和標準差越接近原始圖像，圖像平滑指數越大，則濾波圖片對于原始圖片保留的信息越多，去噪聲效果越好[12]。表3給出了對于同一幅灰度圖片，選取35×35窗口，分別采用均值濾波、高斯濾波和中值濾波時，濾波圖片各指標對比原始圖片的結果。

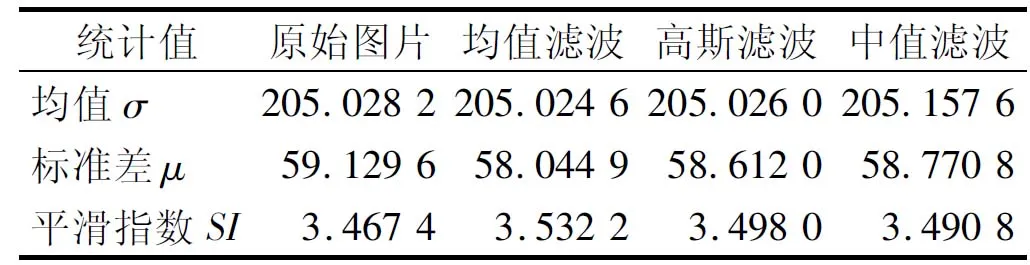
表3 濾波圖片各指標對比原始圖片結果

除此之外，濾波器窗口的大小也會影響到濾波圖片效果。濾波窗口越大，圖片原始信息丟失越多，噪聲抑制效果越好。圖5分別給出了同一幅圖片分別選取5×5，7×7，35×35濾波窗口時的高斯濾波效果。

圖5 不同濾波窗口效果比較

比較表3和圖5可見，高斯濾波在充分抑制背景噪聲的同時，對于原始圖片的信息保留最多。因此，選用窗口尺寸為35×35的高斯濾波器對原始圖片進行濾波處理。

2.2 圖像閾值分割

圖像閾值分割方法主要包括：固定閾值分割、自適應均值閾值分割和最大類間方差法(Otsu)。圖6b)，c)，d)分別給出了固定閾值、Otsu算法以及自適應均值閾值分割的分割效果。

圖6 不同閾值算法的分割效果比較

比較圖6b)、c)、d)3種閾值算法，可以看出，自適應均值閾值算法和Ostu算法都可以很好地將油滴區域和背景區分開來，但前者還可以將油滴區域的邊界顯示出來，并排除掉重疊的油滴區域，因此，本文選取均值自適應均值閾值分割法對油滴區域進行圖像分割。

3 支持向量機算法

在諸多機器學習算法中，SVM算法由于對數據樣本的需求量少，且可以處理復雜的非線性方程，被廣泛應用于圖像識別和故障診斷。

支持向量機理論來自于數據分類問題的處理，試圖尋找一個滿足分類要求的最優分類超平面，使得該超平面在保證分類精度的同時，能夠使超平面兩側的空白區域最大化。理論上，支持向量機能夠實現對線性可分數據的最優分類。隨后，文獻[13]通過引入核映射方法將非線性問題轉化為高維空間的線性可分問題來解決。

圖7給出了支持向量機的分類原理：空心點和實心點分別表示特征空間中2種不同類別的數據；H為能夠將兩類數據正確區分的線；H1和H2為能夠將2種數據分開且平行于分類線的最外側直線，二者之間的距離即為2類數據的分類間隔(margin)。支持向量機的訓練目標就是使分類間隔達到最大，此時H1和H2上的點即為支持向量，H1和H2之間的距離即為兩類數據的最大分類間隔，H則為最優分類線。將其推廣到高維特征空間中，最優分類線則成為最優分類超平面。

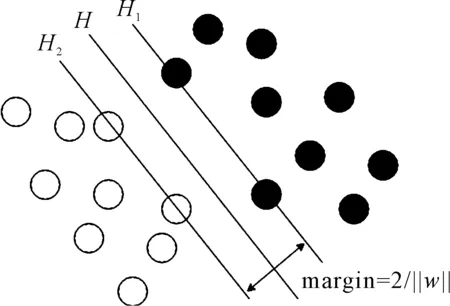
圖7 最優分類面

上述討論僅適用于數據線性可分的情況，在許多問題中，樣本集通常是線性不可分的，此時可以通過適當引入核函數K(x(i),x(j))來實現非線性變換后的線性分類，并不再增加計算的復雜度，核函數的可選種類較多，本文在研究過程中選用學習能力較強，適用范圍廣的Gauss函數。

為了避免數據中某一特征值的權重過大，在進行訓練之前還應該對數據的特征值進行歸一化處理：對于數據點的每一個特征值，依次經過式(1)所示的變換，使其特征值落在[0,1]之間。

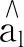
在油滴識別問題中，每張樣本圖片都可以被標記為背景或油滴，因此，該問題是一個二元分類問題，僅需訓練一個分類模型就可滿足要求。使用支持向量機進行油滴識別，學習算法的實施過程如下。

1)對于每一張樣本圖片，提取圖片中每個像元的灰度值作為其特征值，建立樣本的特征向量xi。

2)對每個樣本的特征值進行歸一化處理。

3)標記每個樣本圖片的所屬類別，建立標簽向量yi。

4)輸人特征向量和對應的標簽向量對SVM進行訓練建模。

4 結果分析

4.1 油滴識別

從拍攝得到的原始圖片中選取70張畫面純凈的圖片，經圖像分割后得到343張油滴圖片和514張背景圖片，從857張圖片中隨機抽取770張建立樣本數據集，實驗樣本的組成見表4。

表4 實驗樣本組成

本文SVM算法各項訓練參數設置如下：選取核函數為徑向基函數；設置訓練最優參數值為0.041 4；正則化參數值為8。訓練過程中，共獲取支持向量24個。訓練模型識別測試樣本情況見表5，測試樣本識別正確率為100%，因為：①選用圖像灰度值作為特征值時，油滴與背景的明暗對比度大，油滴與背景灰度值的差值較大，且油滴形狀簡單，易于區分；②SVM算法引入了正則化參數，保證預測誤差盡可能小、回歸函數盡可能平滑，從而提高識別模型的泛化能力。

表5 識別結果

使用該模型對其余204張完整實驗圖片進行識別檢測，累計識別192處油滴，識別正確率超過95%，預測結果可靠。

使用Ostu算法對相同的204張圖片進行識別，表6給出了Ostu算法與SVM算法的用時比較。圖8給出了2種算法在識別過程中的累計用時。

表6 傳統分割算法與SVM時間復雜度比較

圖8 累計用時對比

由表6和圖8可見，SVM算法識別204張圖片的平均用時為0.03 s，比Ostu算法的0.13 s快了76.9%；SVM算法識別204張圖片的總共用時為6.67 s，比Ostu算法的26.14 s快了74.5%；SVM算法的識別效率明顯優于Ostu算法，在識別海量圖片時，本文提出的基于SVM算法建立的識別模型，效率更高。

4.2 油滴粒徑分布

實驗的圓形噴嘴孔徑為2 mm，實驗過程中通過調節齒輪油泵變頻器的頻率以控制油樣流量。油樣流量由注油系統中的精密流量計實時記錄，根據噴嘴口徑換算出油樣初始流速為4.2 m/s。

對識別的油滴粒徑進行統計，得到其粒徑分布在[113.62 μm,7 692.08 μm]范圍內，繪制油滴粒徑出現概率的分布圖(見圖9)。粒徑概率分布屬于左偏態分布，粒徑低于300 μm的油滴占總油滴的73.08%；粒徑低于500 μm的油滴占總油滴的86.81%；粒徑大于2 000 μm的油滴占總油滴的2.20%，該范圍的油滴占比較少，可以忽略。

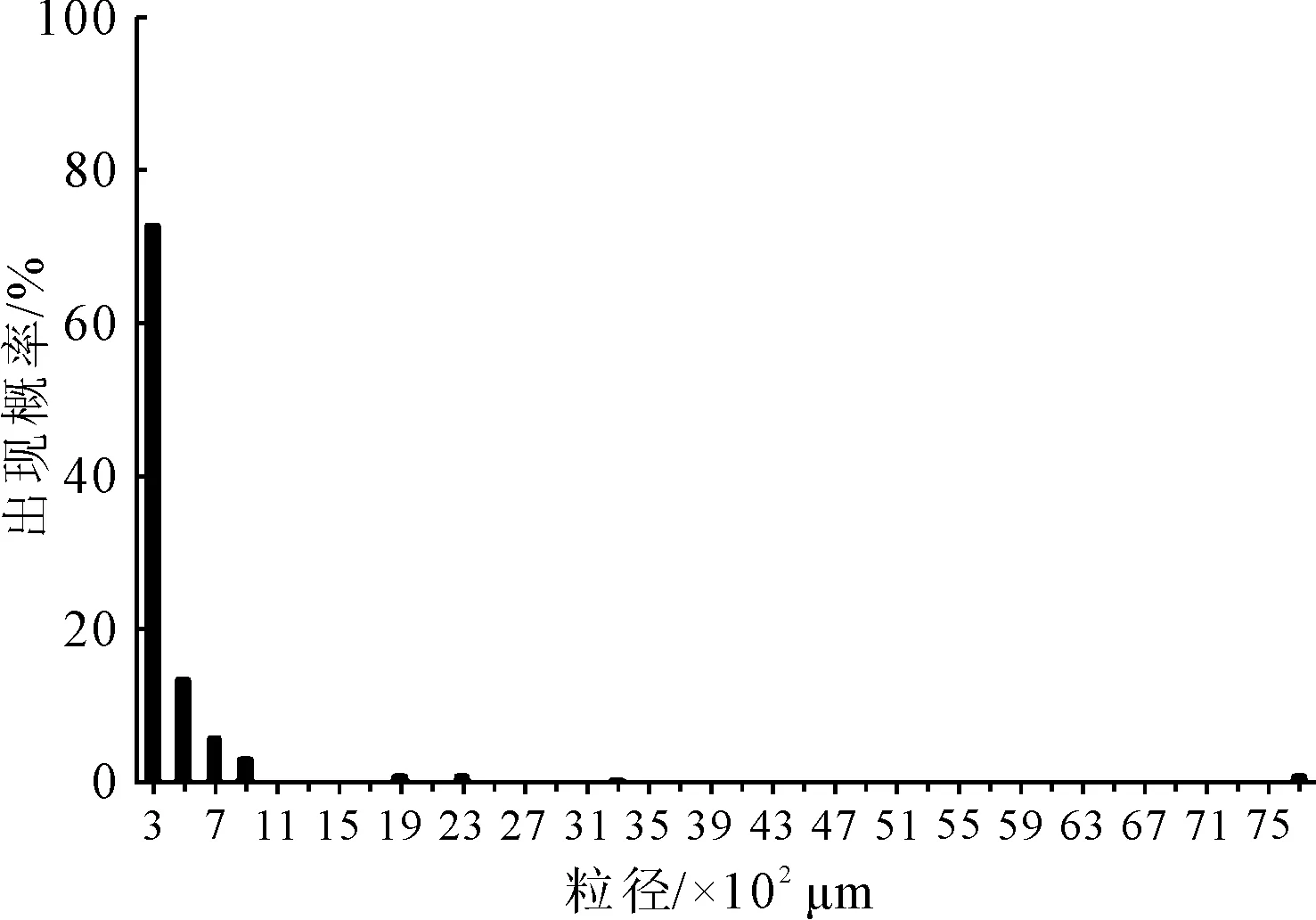
圖9 油滴粒徑出現概率的分布

為了進一步描述識別油滴的粒徑分布情況，引入Rosin-Rammler粒徑分布式(2)。

式中：R(d)為篩下累積率，%；d為識別油滴粒徑，μm；de為臨界粒徑，μm，當R(d)=63.2%時所對應的粒徑；m為均勻性指數，表示油滴粒徑分布范圍的寬窄程度，m值越大，油滴粒徑的分布范圍越窄。

對式(2)取對數得到式(3)。

ln{-ln[1-R(d)]}=mlnd-mlnde

(3)

由式(3)可以看出：當lnd與ln{-ln[1-R(d)]}的回歸線為直線時，油滴的粒徑分布符合Rosin-Rammler，回歸線的斜率為該分布的均勻性指數m，回歸線在橫軸上的截距為臨界粒徑的自然對數lnde。

由式(2)和式(3)，可以計算油滴的中值粒徑d50。

式中：d50為中值粒徑，μm；de為臨界粒徑，μm；m為均勻性指數。

將油滴粒徑d與篩下累積率R(d)代入式(2)和(3)，得到均勻性指數m與臨界粒徑de值分別為1.252 0、251.36μm。

由式(4)得到中值粒徑d50=158.85μm。油滴粒徑d在自然對數坐標系下的分布見圖10，其中的圓點表示識別油滴粒徑的自然對數分布，當lnd>7.7時，在此粒徑范圍中的油滴在整體中占2%，可以忽略。由圖10可見：lnd與ln{-ln[1-R(d)]}大致呈線性回歸關系，協方差R2=0.842 7，表明識別油滴粒徑分布模型符合Rosin-Rammler分布。

圖10 識別的油滴粒徑分布與Rosin-Rammler模型的比較

5 結論

1)將SVM算法應用于油滴識別，用圖片灰度值作為特征值來識別油滴和背景，所訓練模型在測試集樣本識別中正確率達到100%，在油滴圖片識別中正確率在95%以上，識別快速、結果可靠，可應用于海底溢油快速識別、及時采取應急措施。

2)處理204張油滴圖片，SVM算法的平均識別用時比Ostu算法快76.9%，累計識別用時比Ostu算法快74.5%。

3)識別出來的油滴粒徑在自然對數坐標系下呈線性分布，線性回歸的協方差R2=0.842 7，與經典的Rosin-Rammler粒徑分布吻合。

4)SVM算法對油滴進行識別及粒徑分布預測可行，為海底溢油快速識別及應急搶險提供了一種新的思路，具有較好的工程應用價值。