《幾何概型》教學設計

劉英杰

摘 要幾何概型這節(jié)內容，前面有古典概型做基礎，后面延續(xù)了概率的應用，在概率知識部分，起到了承上啟下的作用。在舊知識基礎上，通過類比、歸納與合情推理過渡到幾何概型應該是水到渠成的，但也應該注意幾何概型和古典概型的區(qū)別，如何正確建立幾何概型、正確定位幾何測度是本節(jié)教學的關鍵。

關鍵詞幾何概型;古典概型

中圖分類號：G632 文獻標識碼：A 文章編號：1002-7661（2020）08-0198-01

在一次隨機實驗中，所有可能出現的結果共有限個，也就是說基本事件的個數是有限個，并且每個基本事件的出現的可能性相同，解決這樣的概率問題，可以借助古典概型的計算公式來完美解決。但是對于某些隨機事件，所有可能出現的結果有無限多個。比如，將一根3米長的繩子隨機剪斷為兩截，其中一截大于2米的概率是多少？對于這樣的問題，顯然不再是古典概型的問題，可以借助新的概率模型——幾何概型來解決。

一、創(chuàng)設情境—引入新課

通過一個抽獎游戲回顧古典概型的相關內容。

在長為5米的繩子上等距的掛有6個氣球，其中兩個氣球中設有獎品，現讓某位同學隨機去扎破一個氣球，問該同學獲獎的概率是多大？

然后改變條件得到新的問題。

若繩子的長度不變仍為5米，某同學隨機將一個氣球掛到繩子上的某點，事件A：該點到繩子左端點的距離小于2米，則事件A的概率是多大？

設計目的目的：通過類比引出幾何概型。

本環(huán)節(jié)關鍵：

1、通過與學生的互動，自然引出幾何概型的特點和計算公式。2、分層出現定義的和計算公式，先介紹用長度比表示幾何概型的概率。3、強調幾何概型只和測度比有關，而和區(qū)域位置無關。

二、應用舉例，完善知識體系

應用1：某人午覺醒來，發(fā)現表停了，他打開收音機，想聽電臺整點報時，求他等待的時間不多于10分鐘的概率。

目的：學生參與，通過討論交流得到不同的解決方案，老師點撥進一步挖掘幾何概型的特征。完善定義和計算公式（用面積和體積比表示事件發(fā)生的概率）

應用2：在某檔電視綜藝節(jié)目中，有一個現場互動的環(huán)節(jié)，由主持人邀請一名觀眾從兩個小游戲中任選一個去玩兒，若觀眾在游戲中獲勝，便可領取一份精美的紀念品。

游戲需要借助一個矩形來完成，具體游戲規(guī)則如下：

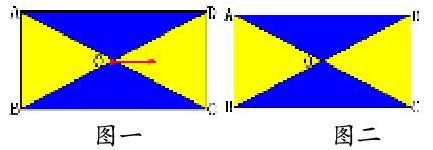
游戲一：觀眾隨機向長方形區(qū)域內扔一粒豆子（圖1），若豆子擊中藍（深）色區(qū)域，則觀眾獲勝。

游戲二：觀眾隨機撥動長方形中心的紅色指針，若指針停止轉動時停在在藍（深）色區(qū)域（圖2），則觀眾獲勝。

如果你是參與互動環(huán)節(jié)的一名觀眾，你會選擇哪個游戲去玩兒？說明你的理由。

目的：1、通過對比讓學生體會解決幾何概型問題，明確基本事件和正確選擇測度的重要性。2、利用數學知識做出理智的選擇，由于兩個游戲的背景很相似，但研究方法又不相同，細致的同學更容易在審題的第一時間發(fā)現兩者的區(qū)別，另一些同學更容易總結出解決問題的規(guī)律。肯定不同學生自身長處的同時，引導學生彌補自己的不足也是本環(huán)節(jié)的重要任務。

三、關注民生，能力提升

某公交站點，只有1路和2路公交車停靠，1路車每天早晨6：10第一趟車到達本站，以后每隔15分鐘，有一趟車停靠;2路車每天早晨6：15第一趟車到達本站，以后每隔15分鐘，有一趟車停靠。市民張先生每天上班乘坐1路或2路車都可以到達工作單位，張先生每天6：00～7：00之間隨機到該站候車，來車就上。張先生經過20天的連續(xù)記錄發(fā)現，他有13次乘上1路車，只有7次乘上2路車，張先生認為1路和2路公交車每兩趟車之間的時間間隔相同，且在6：00～7：00間都有4趟車經過，所以他乘上1路和2路車的機會應該大致相等，于是張先生懷疑2路車有經常晚點和少發(fā)車次的情況發(fā)生，準備向公交公司投訴此事，你是否支持張先生的觀點？

目的：1、通過實例引起學生的興趣，并在解決問題的過程中引導學生把抽象的時間轉化為具有具體幾何特征的線段然后采用幾何概型的知識來解決問題。讓學生體會數學來源于生活并服務于生活。2、培養(yǎng)學生的抽象概括能力，數學建模能力。（注意：既可以轉化成線段模式也可以轉化成圓周模式。）3、在思辨中，讓學生學會用數學的眼光去觀察世界，用數學的思維去認知世界，從而提升認知能力。

四、小結

1、幾何概型的概念、特點、計算公式;幾何概型與古典概型的對比，用幾何概型求概率的步驟等。2、概率知識在生活中應用及意義。3、通過生活中的實例讓學生感受到數學在實際應用中的重要性和廣泛性，從而無痕地喚醒學生學習興趣，并根據自身特點，合理規(guī)劃自己的學習。

基金項目：本文系2018度河北省“三三三人才”人才資助項目課題《生涯規(guī)劃在數學課堂中的滲透》成果，項目編號：A201803084。