“反例法”在中學數學解題中的應用
張慶大

[摘要]在數學解題中應用“反例法”可以有效提高解題效率,拓寬解題思路.教師在課堂教學和問題訓練中應讓學生充分體會反例,進一步訓練學生的辯證思維.
[關鍵詞]中學數學;反例法;解題
[中圖分類號]
G633.6
[文獻標識碼] A
[文章編號] 1674-6058(2020)17-0014-02
在數學教學中,師生往往是指出正確的命題,并專注于獲得正確的解決方案,而忽略了如何找出錯誤.舉反例是發現并糾正錯誤的普遍方式.反例可以豐富和深化學生的抽象理解,特別是對一些數學理論的掌握大有裨益;反例也可以形成清晰認知,特別是對數學性質、概念、定理等的理解.教師列舉的反例必須遵循從一般到特殊的原則,并具備形象化、直觀性、代表性等諸多特性,使學生容易學習、掌握、理解,學生的感知印象能夠在理解反例中得以增加,使學生透徹理解所學的知識.
一、反例的概念
在數學中,反例一般指的是對某理論和概念的結論相反的例子,但其條件完全相同.從某種程度上說,所有例子都可以作為反例來使用,因為它總是可以指出一定的命題是錯誤的.然而,我們所研究的反例,它是一種基于已在數學領域被證明并且具有一定作用的理論和邏輯推理的反面教材.一個反例可以看作是證明的特殊方法.一般來說,反例有許多個,我們列舉反例時,只需要選出其中的一個就可以了.數學的反例可以分成下面的幾種.
1.基本形式的反例
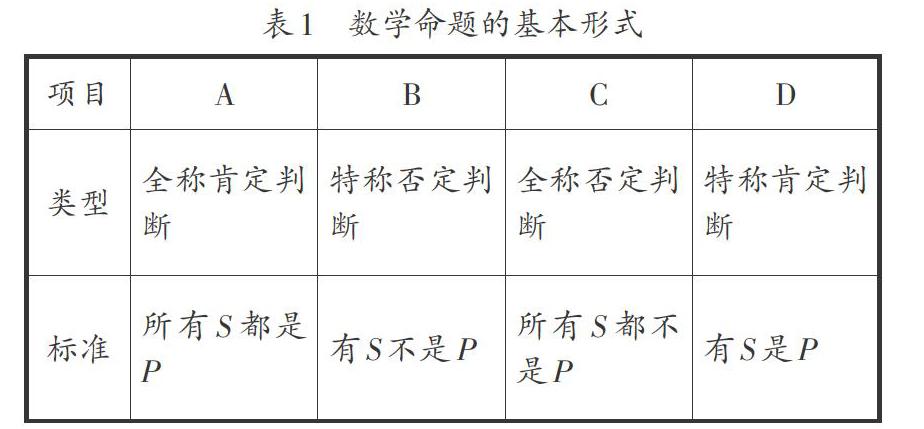
數學命題可以分成四種基本的形式:全稱否定判斷,全稱肯定判斷,特稱否定判斷,特稱肯定判斷.(如表1).
2.關于必要條件假言判斷和充分條件假言判斷的反例
充分條件就是某種事物是另一種事物的充分條件,前者可以推出后者.能夠表述為“P→Q”,即“有P必然有Q”.反過來“沒有P,不一定說明沒有Q”.能夠舉出反例“沒有P,卻可以有Q”.這種反例則稱為關于充分條件假言判斷的反例.
必要條件就是某一種事物是另一種事物的必要條件,后者能推出前者.能夠表述為“P Q”,也就是說“沒有P,一定沒有Q”,但是“有了P,卻不一定有Q”.能夠舉出反例“有了P,沒有Q”.
3.條件變化型反例
條件變化型反例是在數學命題中的條件改變后發生的,且結論與原先條件下會有不同,條件的變化可以分為較多的形式.如命題條件的增減以及相應參數的改變.這樣的反例形式對于教學和理論的研究有著較大的作用.
二、反例的作用
通過舉出反例的方法,可以進一步促進新的方法和概念的產生.在數學的歷史發展過程中,很多理論的更新以及創造都是由反例得出的.這也讓反例在數學領域不斷被應用,并起到重要的作用.在數學定理和概念中有許多結構復雜的情況,貫穿其中的結論,有時很難理解.反例可以使概念更加清晰、明確,并能使定理、結論之間的充分性和必要性非常明顯.數學中有特別多這樣的反例.數學是一門嚴謹的學科,有很強的學科性,有自己獨特的思維特色和獨立的邏輯推理體系,不能僅僅憑借著直觀和客觀去了解和理解它,這樣會對其形成模糊的認知.然而數學教學的過程中,讓學生了解嚴謹的邏輯推理和思維特點的同時,還應該掌握各類的反例,這樣才能夠使學生牢牢鞏固數學基礎知識和基本技能,提高數學修養與培養科學思維及創新能力.
三、構造反例的方法
1.分類法
分類是數學思維的一種非常重要的方式.通過將一堆事物進行歸類,將其中具有一定特征的事物放到一起的方法就叫作分類法.它可以減少尋找反例的范圍,避免盲目使用反例進行論證.如何利用分類法列舉出反例就成了關鍵問題.一般地,可以先把題設條件分成甲、乙兩大類,命題成立屬于甲類,命題不成立屬于乙類;然后再在乙類中舉出一個相反的例子.
[例1]命題“平面外的兩條平行線在該平面內的射線是平行線”對嗎?為什么?
分析:這個命題在已經給出的條件下看似正確,但是卻沒有考慮兩條平行線是否與平面平行.這樣很容易舉出反例進行說明.
如圖1所示,當兩條平行線a、b都與平面a垂直時,它們在a內的射影為兩個不同點A、B,而不是兩條相互平行的線.因此該命題是錯誤的.
分類法可以有效識別命題中的條件,并且可以避免遺漏相關條件以至于推出的結論出現錯誤.
2.特殊化法
特殊化法就是在命題的條件下,舉出一些較為特殊和極端的例子,以證明該命題是否正確.
分析:把x=-2代入不等式中可知x=-2是它的一個解,所以B、C、D都不對,故選A.
由本題x=-2就是B、C、D的一個反例.可以看出舉反例是解選擇題的一種巧妙方法.
3.窮舉法
[例3]命題“在△ABC中,BC邊上的高AD等于BC,H是垂心,M是BC的中點,則MH+DM=1/2Bc”是否正確?為什么?
分析:這道題的易錯點在于,常規的方法只考慮角B和角C小于90°的情況,而忽略了其他的情況.
當∠C=90°時,如圖2所示.
關于三角形的命題,在解答時不能只考慮一種角度,而是要考慮多種角度在命題條件下是否成立.
4.推理分析法
推理反例主要是通過命題給出的條件,根據相關的理論和原理推出相應的結論.
這些都是常見的解決實際應用題的方法,對學生的思維訓練非常好.國外研究者對于反例的作用早有闡釋,并且證明其在應用中可以激發學生去探索數學奧秘.因此,在課堂教學和習題訓練中讓學生充分體會反例,有利于學生有效學習,能進一步訓練學生的辯證思維.
[參考文獻]
[1]黃建橋巧用反例學習數學:論初中數學教學反例的運用[J]教育界:綜合教育研究,2018(1):77-78.
[2]盧成,俞春三視圖表示的幾何體不唯一的另一反例[J]中學數學教學,2017(6):29
(責任編輯 黃桂堅)

