運營期高速鐵路軌道長波不平順靜態測量方法及控制標準

楊 飛，趙文博，高芒芒，孫加林

（中國鐵道科學研究院集團有限公司 基礎設施檢測研究所,北京 100081）

軌道不平順包含不同的波長成分,不同波長成分對列車運行安全性、舒適性的影響也不相同［1-2］。列車速度越高,影響列車動力響應的軌道不平順波長也越長。由于軌道長波不平順整治比較困難,并且動態檢測較為復雜,因此對于疑似是由長波不平順引起的“晃車”區段,應首先對其進行靜態測量復核。

我國對軌道長波不平順的靜態測量主要借鑒德國的矢距差法［3］。由于矢距差法計算模型較為復雜,日常檢測時常常對其簡化,利用簡化的矢距差公式對軌道長波不平順進行評價。隨著我國高速鐵路運營年限的增加,以及受外界環境因素的影響,部分高速鐵路基礎已出現較大的變形問題［4］,采用現有的矢距差法或者簡化矢距差法測量,結果都明顯超出驗收標準,而我國又無運營期高速鐵路軌道長波不平順靜態控制標準,且超過驗收標準的區段大部分列車實際運營狀況良好,如綜合檢測車檢測的動態軌道長波不平順和車輛振動加速度均無明顯響應,使高速鐵路運營時現場維修部門無法準確查找確實有影響的軌道長波不平順,導致復核及養修的不便利。

對于軌道長波不平順,國外其他國家如日本選用40 m 弦對新干線軌道進行測量［5］。法國采用與日本一樣的測量方法,認為2 個轉向架之間的總長約為33 m,只要控制好33 m 弦測量得到的幅值就能保證行車的舒適性,因此法國采用了高低31 m弦、軌向33 m 弦測量結果評價軌道長波不平順。韓國建議高速鐵路25 m以上波長不平順應采用30 m或40 m長弦進行測量［6］。

本文在分析現有高速鐵路軌道不平順靜態測量方法的基礎上,采用實測數據及理論分析相結合的手段,研究國內現行高速車輛動力響應與軌道不平順的匹配關系,提出更為準確的軌道長波不平順靜態測量方法及相應幅值控制標準。

1 現有測量方法

1.1 矢距差法

矢距差法通過計算一定弦長范圍內各測點間的相對點位關系評價軌道平順性,目前我國主要通過300 m（480a,其中a為扣件間距）弦長范圍內、相距150 m（240a）任意2 個測點間的矢距差評價靜態軌道長波不平順［4］,測量示意圖如圖1所示。圖中：Pi為軌枕測點編號,i=0,1,2…；ri為第i測點處的矢距。

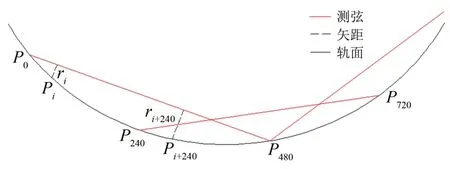
圖1 矢距差法測量示意圖

矢距差法計算軌道不平順的公式為

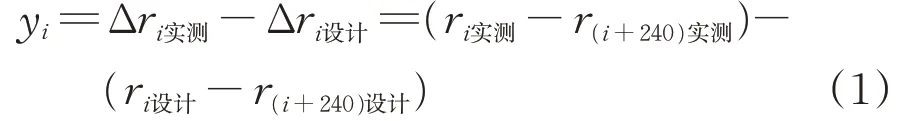
式中：yi為矢距差法檢測的第i測點處軌道不平順；Δri實測為第i測點處軌道不平順實測矢距差；Δri設計為第i測點處軌道不平順設計矢距差；ri實測和ri設計分別為第i測點處的實測和設計矢距。

1.2 簡化矢距差法

矢距差法計算的矢距垂直于測弦,屬于軌道內部幾何參數［7］,與軌道精調時沿線路橫向和垂向調整不一致,容易引起混淆。而現場多通過測量軌道高程偏差、中線偏差等外部幾何參數對軌道不平順進行評價,因此需要將內部幾何參數轉換成需要的外部幾何參數,轉換模型如圖2所示。圖中：Pi’為各測點設計編號；α為測弦兩端點與水平基準面的夾角（近似等于0）。

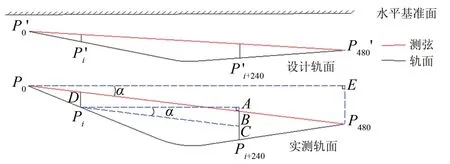
圖2 矢距差法計算模型

根據式（1）,利用圖2中幾何關系得

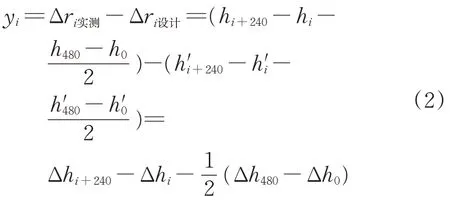
式中：hi為實測軌面測點至水平基準面的高程；hi’為設計軌面測點到水平基準面的高程。

式（2）將測量結果中的矢距轉換成了軌道高程,既簡化了計算,又使得物理模型更加清晰。其中,等式右邊第1 項為第i+240 測點高程變化量,第2 項為第i測點高程變化量,第3 項為測弦兩端點高程變化量之差。當測弦上2 個端點軌道高程變化量之差相等時,即軌道結構在測弦范圍內均勻變形時,第3項等于零,矢距差法可以簡化為

式（3）為軌道不平順的簡化矢距差法計算公式,為現場測量中常用的計算方法,用間隔150 m（240a）的2個測點的高程變化量之差表示矢距差。

1.3 測量方法適用性

1）傳遞函數檢驗

實測軌道不平順數據經過采用矢距差法處理后得到新的軌道不平順數據,輸入的實測軌道不平順幅值與輸出的新的軌道不平順幅值之間的關系可以用傳遞函數表示。由于軌道不平順為隨機不平順,包含不同的波長成分,為研究不同波長軌道不平順經過矢距差法處理后的幅值及相位變化,需要對式（2）和式（3）作傅里葉變換,可分別得到矢距差法和簡化矢距差法的傳遞函數H（ω）。

采用矢距差法時,

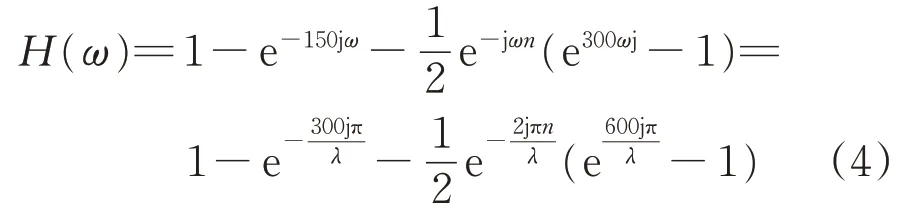
式中：ω為空間角頻率,rad·m-1,ω=2π/λ；λ為軌道不平順波長；j為虛數。

采用簡化矢距差法時,

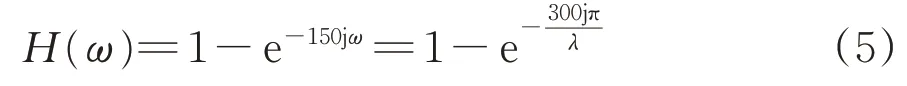
從式（4）和式（5）看出,2 種計算方法得到的傳遞函數都包含虛部,即測量結果與實際軌道不平順存在相位差,表現為軌道不平順的測量位置并非其實際位置,有一定的偏移。

對2 種方法的傳遞函數幅頻響應進行計算,結果分別如圖3和圖4所示。由圖3和圖4可以看出：矢距差法傳遞函數的幅頻響應受軌道不平順波長和測點位置的共同影響,幅頻響應在-0.42～2.4 之間振蕩；簡化矢距差法傳遞函數的幅頻響應只受軌道不平順波長的影響,與測點位置無關,幅頻響應在0～2之間振蕩。

2）實測數據檢驗

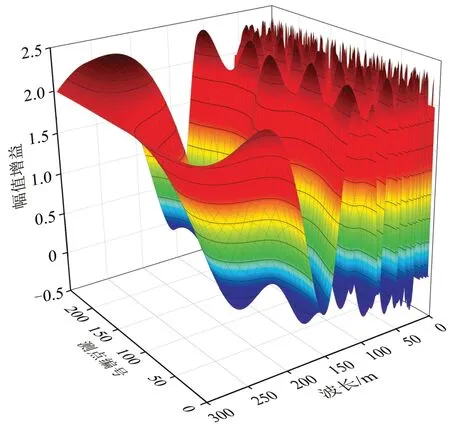
圖3 矢距差法傳遞函數

由于以上分析主要考慮了運營期高速鐵路路基變形問題,因此主要針對路基變形引起的軌道垂向變形及相應車輛的垂向振動進行研究,后續若未特別說明,“軌道不平順”和“車體加速度”均指的是“軌道高低不平順”和“車體垂向振動加速度”。選取某段運營期高速鐵路,分別利用矢距差法和簡化矢距差法計算軌道不平順,同時截取相應區段綜合檢測車檢測的車體加速度進行對比,結果如圖5所示。圖中：g為重力加速度。

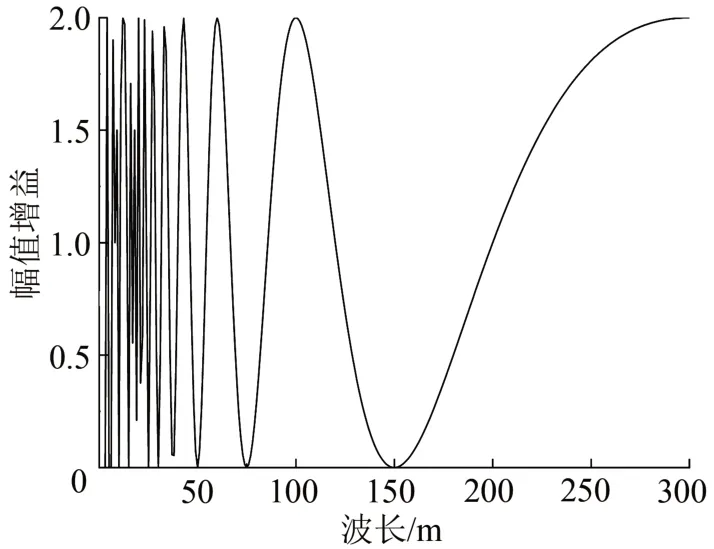
圖4 簡化矢距差法傳遞函數

由圖5可以看出：整個區段根據軌道不平順大致可以分為區段1 和區段2,區段1 軌道不平順幅值明顯大于區段2,但是2 個區段的車體加速度差別不大；點A3的車體加速度大于點B3,然而矢距差結果卻是點A1小于點B1,盡管簡化矢距差法測量結果中點A2大于點B2,但是車體通過點A和點B這2 個位置時車體加速度與軌道不平順并無明顯相關性；另外,從區段1 軌道不平順數據可以看出,簡化矢距差法測量結果明顯大于矢距差法,且2 種方法的測量結果都遠遠超過高速鐵路無砟軌道維修規則規定的10 mm/150 m/300 m 限值（即300 m弦長,間隔150 m,2個測點矢距差不超過10 mm）。以上結果都說明矢距差法和簡化矢距差法測量結果與車體動力響應匹配性較差,不適用于運營期高速鐵路軌道長波不平順的靜態測量。

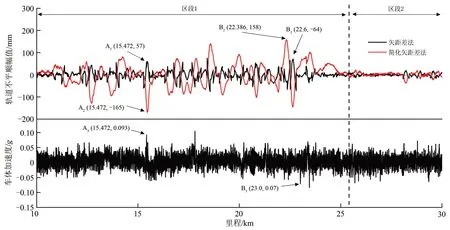
圖5 不同方法得到的軌道不平順與車體加速度相關性

2 60 m 弦中點弦測法

2.1 中點弦測法

我國目前采用測弦長度為10 m 的中點弦測法（簡稱10 m 弦中點弦測法）進行軌道中波不平順的靜態測量,其測量示意圖如圖6所示。圖中：L為半弦長,則測弦長度為2L。在計算時,由于測弦長度遠大于測弦兩端點高程偏差,因此檢測時測弦與水平基準面夾角很小［8］,此時yi可近似為中點弦測法矢距,為

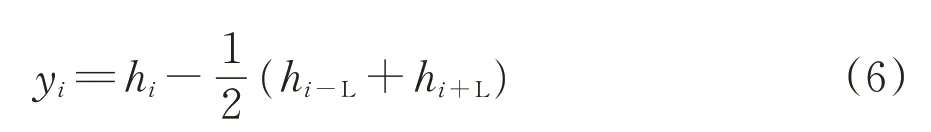
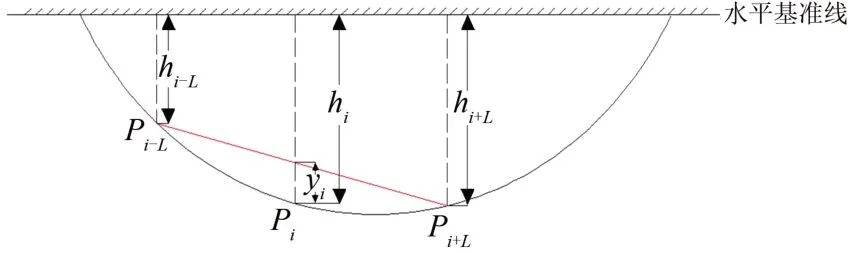
圖6 10 m中點弦測法測量示意圖

2.2 60 m弦中點弦測法

由式（6）可以看出,采用中點弦測法時測量結果受測弦長度2L的影響,不同測弦長度測量軌道不平順結果不同,因此需要選取合理的測弦長度。車體動力響應受軌道不平順的影響,尤其是當軌道不平順波長在列車敏感波長附近時,車體振動劇烈,因此弦測法測量軌道不平順波長范圍應涵蓋列車敏感波長,而不同測弦長度能夠測量的有效波長范圍不同,因此需要結合中點弦測法不同測弦長度有效測量波長范圍以及列車敏感波長確定中點弦測法合理的測弦長度,具體流程如圖7所示。

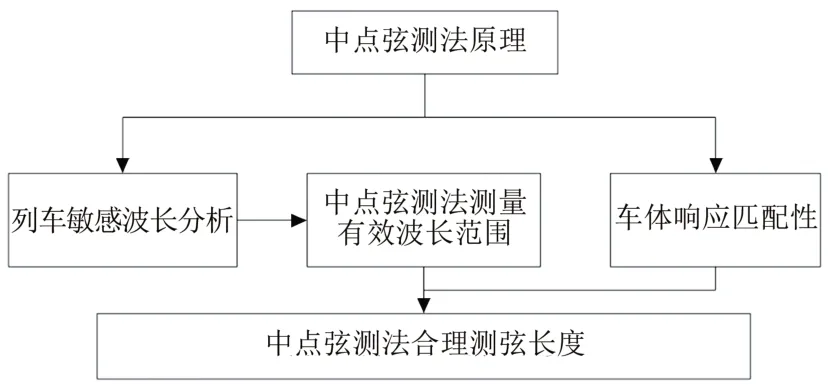
圖7 中點弦測法合理的測弦長度確定流程

1）不同測弦長度測量有效波長范圍

中點弦測法采用固定測弦長度進行測量,因此對于過長或過短波長的軌道不平順不能有效測量［9-10］,其有效測量范圍可根據傳遞函數進行計算。根據式（6）可得傳遞函數表達式為

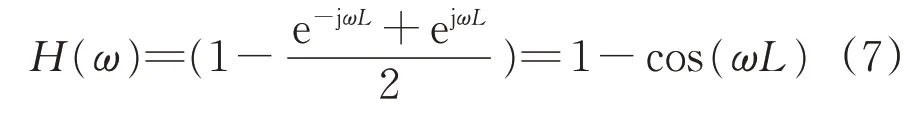
由式（7）可以看出,中點弦測法傳遞函數受軌道不平順波長λ（λ=2π/ω）和測弦長度L的影響,且傳遞函數中不存在虛部,說明測量結果與實際結果不存在相位差,可以準確測得實際位置的軌道不平順。

分別采用10,40 和60 m 測弦長度時得到的軌道不平順波長和幅值增益的關系如圖8所示。從圖8可以看出：中點弦測法傳遞函數在0～2.0 之間,若以傳遞函數不小于1.0 為有效測量,可分別得出10,20,30,40,50 和60 m 弦對應的有效測量波長范圍分別為7～20,13～40,20～60,27～80,33～100和40～120 m。

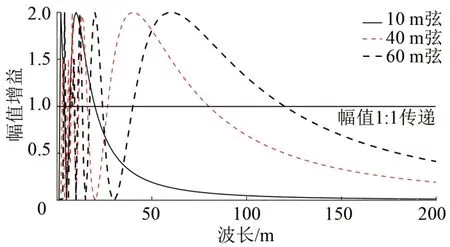
圖8 中點弦測法有效波長范圍

2）列車敏感波長

收集綜合檢測車2 次檢測數據,選取某運行速度為300 km·h-1區段,得到車體加速度功率譜密度如圖9所示。由圖9可以看出：低頻區段車體垂向振動加速度空間頻率集中分布在0.013 67～0.015 63 Hz 范圍內,對應波長為64～73 m,該波長即為車速300 km·h-1時的車體垂向敏感波長；低頻區段車體橫向振動加速度空間頻率集中分布在0.009 8 Hz 附近,對應波長為102 m,該波長即為速度300 km·h-1時的車體橫向敏感波長。

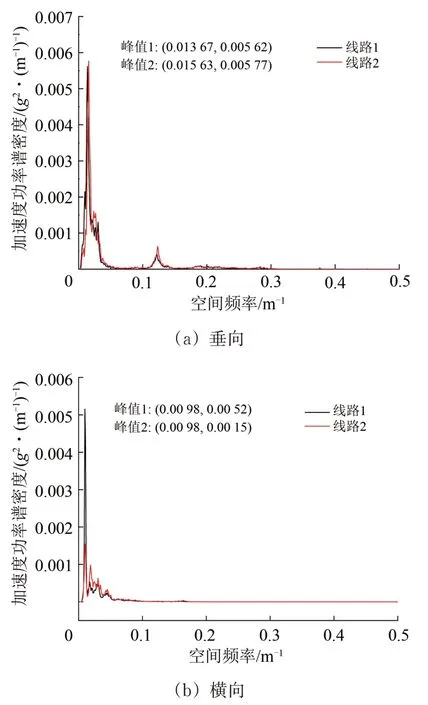
圖9 綜合檢測車車體振動加速度功率譜密度

對于同一型號列車,車體自振頻率一定,根據列車敏感波長與運行速度的關系即式（8）可看出,影響列車振動的軌道不平順波長隨著速度的提高而增大。

式中：λs為敏感波長,m；v為列車速度,km·h-1；f為車體自振頻率,Hz。

已知速度300 km·h-1列車敏感波長,可以得出速度350 km·h-1列車敏感波長,結果見表1。從表1可以看出：對于現行速度最高為350 km·h-1線路,軌道不平順管理波長應不小于120 m,而測弦長度為60 m 時中點弦測法（簡稱60 m 弦中點弦測法）的有效測量波長范圍為40～120 m,因此確定測弦長度為60 m,即可滿足軌道不平順管理波長的要求。

表1 不同速度時的列車敏感波長

3）車體響應匹配性

中點弦測法計算公式具備2階差分的形式,與軌道不平順的2階導數相關,從動力學角度來看,中點弦測法結果形式與車體加速度一致,因此需要研究中點弦測法軌道不平順與車體加速度的匹配性。采用包括適用于軌道中波不平順靜態測量的10 m弦等不同弦長測量軌道不平順,并與車體加速度進行對比,結果如圖10所示。從圖10可以看出：10 m 弦測量的軌道不平順與車體加速度相關性較差,40 m弦和60 m 弦測量的軌道不平順與車體加速度相關性較好。

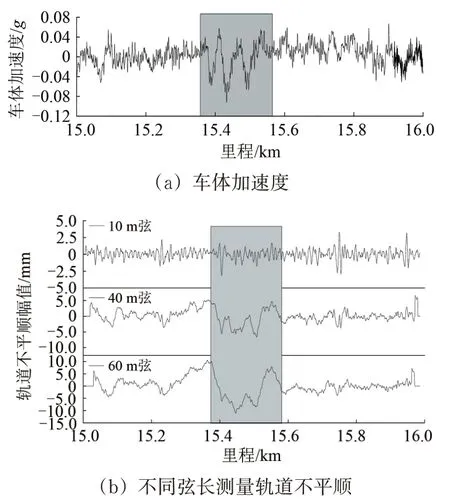
圖10 不同弦長中點弦測法測量軌道不平順與車體動力響應對比

同理,對多個檢測區段采用不同測弦長度得到的軌道不平順測量結果與車體加速度相關性進行分析,得到相關系數均值見表2。從表2可以看出：40,50 和60 m 弦軌道不平順測量結果與車體加速度的相關性明顯優于10,20和30 m弦。

表2 相關系數均值

以上對矢距差法、簡化矢距差法及不同測弦長度中點弦測法的計算原理及特性進行了分析,為得出評價軌道長波不平順的合理方法,需對以上方法的優劣性及適用性進行對比,結果匯總見表3。

表3 不同測量方法的優劣性

從以上分析得出：矢距差法和簡化矢距差法都存在相位差,導致測量結果偏離實際位置,且測量結果明顯大于實際軌道不平順；此外,由于運營期高速鐵路路基存在不均勻變形,從原理上來說矢距差法不能進行簡化；10 m 弦中點弦測法由于測弦長度太短,不能有效測量長波不平順,導致測量結果與車體動力響應匹配性較差,因此都不適用于運營期高速鐵路軌道長波不平順靜態檢測；60 m 弦中點弦測法檢測特性明顯優于以上幾種方法,且有效測量軌道不平順波長范圍為40～120 m,滿足列車敏感波長及軌道長波不平順管理波長的需要,因此建議采用60 m 弦中點弦測法對運營期軌道長波不平順進行靜態測量。

3 軌道長波不平順控制標準

收集綜合檢測車在速度為300 km·h-1時的檢測數據,采用60 m 弦中點弦測法可以得到一系列軌道不平順及對應的車體加速度數據,同1個軌道不平順會得到1組對應的車體加速度,為保證行車安全性和乘客舒適性,統計每個軌道不平順所對應的1組車體加速度的均值、標準差,在95%置信區間下求每個不平順幅值所對應的最大可能加速度,并研究車體加速度與軌道不平順幅值之間的關系,如圖11所示。從圖11可以看出：車體加速度與軌道不平順近似呈線性關系,采用最小二乘法進行擬合,得出時速為300 km 時車體加速度與軌道不平順幅值之間的關系為車體加速度=0.008×軌道不平順+0.028。

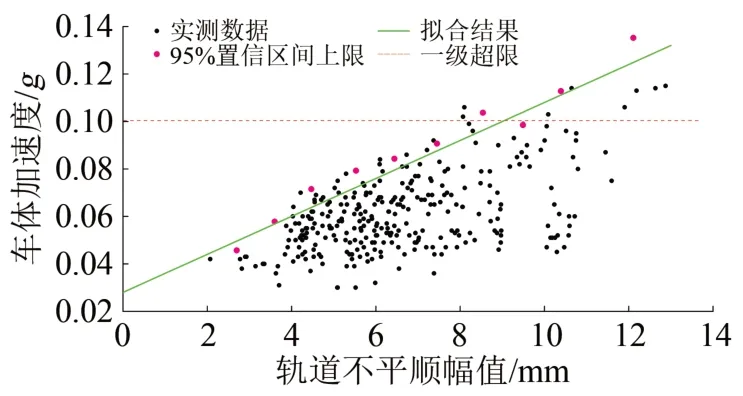
圖11 軌道不平順與車體加速度關系

以車體加速度為控制標準,得出60 m 弦中點弦測法測量運營期高速鐵路軌道長波不平順控制標準建議值見表4。

表4 時速300 km運營期高速鐵路60 m弦中點弦測法的軌道長波不平順控制標準建議值

由于實測350 km·h-1檢測數據較少,不能采用統計方法,基于以上300 km·h-1控制值,需要研究列車運行速度與加速度之間的關系,進而推斷速度為350 km·h-1時的控制標準建議值。日本根據運營經驗得出,車體振動加速度的增幅可按照正比于列車速度1.5次方來推斷［11］,即

式中：a1和a2為車體加速度；v1和v2為列車速度。

利用多體動力學仿真軟件UM建立車輛動力學仿真模型,如圖12所示。

圖12 車輛動力學仿真模型

設置余弦型不平順［12］,波長一定,幅值為10～30 mm,計算各種速度工況下,車體加速度與速度的關系,結果如圖13所示。從圖13可以看出：對于速度分別350 和300 km·h-1,車體加速度比約為速度比的1.25 倍,與式（9）計算結果1.26 基本一致。

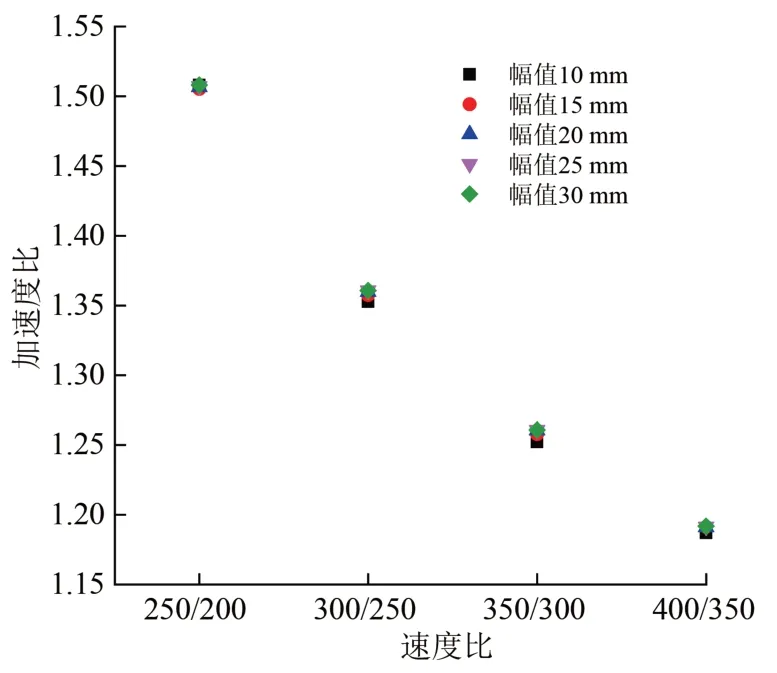
圖13 不同軌道不平順下加速度比與速度比關系

因此可以根據表4及車體加速度與列車速度之間的關系,以車體垂向加速度為控制指標［13］,得出速度為350 km·h-1,60 m弦中點弦測法測量運營期高速鐵路軌道長波不平順控制標準建議值見表5。

表5 時速350 km運營期高速鐵路60 m弦中點弦測法的軌道長波不平順控制標準建議值

4 實例驗證

60 m 弦中點弦測法可通過軌檢儀矢距測量系統利用“以小推大”進行測量得到,也可基于CPIII 控制網通過軌測儀先測得軌面絕對位置,然后利用式（6）計算獲得,后一種方法精度較高。某運營期高速鐵路區段軌測儀檢測得到的實測軌面高程偏差如圖14（a）所示,得到的60 m 弦中點弦測結果如圖14（b）所示。

為驗證60 m 弦測法的有效性,對上述區段按照350 km·h-1檢測標準進行評價,得出部分超限區段,其中K58+175 區段軌道高低不平順波形如圖15所示。由圖15可以看出,軌道長波高低不平順最大幅值達到10.65 mm。

圖14 實測軌面高程與中點弦測法結果對比

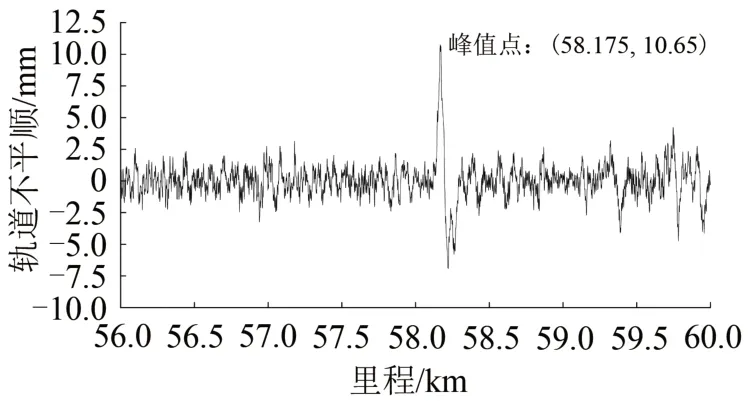
圖15 60 m弦中點弦測法測量結果

綜合檢測車以速度292 km·h-1對本區段進行檢測,動態檢測結果如圖16所示。由圖16可以看出,軌道長波高低不平順峰值為8.5 mm,同樣超過動態檢測Ⅰ級維修標準,車體加速度達到0.098g,基本接近Ⅰ級標準［14］,表明60 m 弦中點弦測法測得的軌道長波不平順與車體振動加速度匹配性較好,可以準確發現影響運營舒適性的區段。

圖16 動態檢測結果

針對以上區段,現場根據60 m 弦中點弦法的測量結果進行了及時維修,得到維修后60 m 弦中點弦測結果如圖17所示。由圖17可以看出：軌道長波高低不平順幅值明顯降低,在K58.175區段附近最大值為4.9 mm,出現在K58+337 處,低于軌道長波高低不平順Ⅰ級維修標準。

綜合檢測車以352 km·h-1速度對本區段進行檢測,結果如圖18所示。由圖18可以看出,維修后軌道長波高低不平順峰值為1.27 mm,車體垂向振動加速度峰值0.04g,均遠低于動態檢測Ⅰ級維修標準,表明60 m 弦中點弦測法測得的軌道長波不平順可以較好地指導現場養護維修。

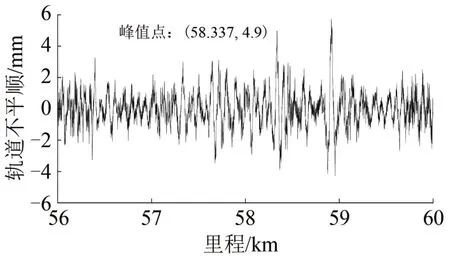
圖17 維修后60 m中點弦測結果

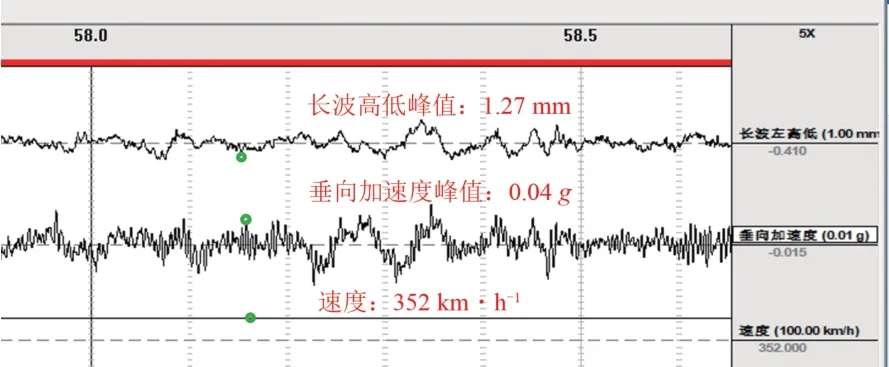
圖18 維修后動態檢測結果

5 結 論

（1）根據矢距差法、簡化矢距差法的檢測特性以及實測數據分析,可知現有軌道長波不平順測量方法與實際結果存在與檢測起點相關、含有里程相位差、基礎變形時檢測幅值偏大、與車體振動加速度匹配性較差等問題,不適用于運營期高速鐵路軌道長波不平順的靜態檢測。

（2）中點弦測法測量結果與車體加速度匹配性較好。根據加速度譜分析,影響車體響應的最大不平順敏感波長接近120 m；從中點弦測法測量有效波長范圍以及不同弦長與車體加速度相關性可以知道,選用60 m弦中點弦測法既可以滿足軌道不平順管理的需要,又可以很好地與車體動力響應匹配。因此,建議選用60 m 弦中點弦測法作為我國時速300～350 km高速鐵路軌道長波不平順靜態測量方法。

（3）利用60 m 弦中點弦測法得到的軌道不平順與車體振動加速度的關系,以及車體振動加速度與速度的關系,給出速度300 km·h-1運營期高速鐵路60 m 弦中點弦測法的軌道長波高低不平順3級控制標準建議值分別為9,15,21 mm；借助動力學仿真分析,推演出速度350 km·h-1運營期高速鐵路60 m 弦中點弦測法的軌道高低不平順3 級控制標準建議值分別為7,11,15 mm。

（4）利用提出的60 m 弦中點弦測法對實際運營期線路進行評價,結果表明采用該法得到的軌道長波不平順與車體振動加速度匹配性較好,可以準確地發現影響運營舒適性的區段；利用60 m 弦中點弦測法測量結果開展維修工作,可以使軌道不平順幅值明顯降低,起到了更好地指導現場養護維修工作的效果。