基于延遲脫體渦算法高速列車通過隧道時的繞流特性

楊廣雪，劉志明，劉秋澤，董 磊，周君峰

（1.北京交通大學 機械與電子控制工程學院,北京 100044；2.中車長春軌道客車股份有限公司 轉向架開發部,吉林 長春130062；3.中車青島四方機車車輛股份有限公司 技術中心,山東 青島266111）

高速列車通過隧道時：由于氣動效應和地面效應的共同影響,繞流更加復雜,對列車及周圍環境產生更嚴重的影響；列車運行阻力會明顯增大,甚至可能高出明線運行的4倍以上,對列車的安全運行提出了更高的要求［1］；在隧道和列車之間會產生強烈的壓力波動,誘發列車內壓力波動加劇,降低車輛的乘坐舒適性［2-3］；由于列車運行軌跡偏離隧道中心,車體兩側的壓力波動差增大,使得列車橫向振動加劇,從而降低列車的運行穩定性［3］；列車在通過隧道出口、入口時車身結構受到的壓力幅值可分別高達4 和7 kPa 左右,遠遠超出明線運行時的壓力幅值,這會對列車相關結構的承載強度造成更大的影響［4］；列車在進入隧道時的擠壓效應會在隧道的出口部位產生壓力波動,對周圍的環境產生噪聲污染和振動影響［5］。基于這些原因,進行高速列車過隧道繞流特性研究具有重要的理論意義和工程應用價值,但國內外針對高速列車通過隧道時的繞流特性研究仍缺乏較為全面的分析。

目前,高速列車繞流的模擬方法主要包括：直接數值模擬（DNS）、大渦模擬（LES）、雷諾平均方法（RANS）和脫體渦模擬（DES）［7-10］。DNS 方法通過直接求解流體運動的N-S 方程,計算精度最高且結果最詳細,但對網格分辨率和計算資源要求很高,就目前的計算機水平而言,直接將DNS 方法應用于高速列車的繞流模擬仍不現實,除非是在極其簡化條件下才是可行的；周瑜［11］通過求解減少一個維度的二維非定常黏性可壓N-S方程,對極其簡化的高速列車模型通過隧道時的流場進行了數值模擬,得到了不同時刻系統二維流場云圖。LES 方法通過先對大尺度渦和小尺度渦過濾,然后分別對小尺度渦用模型求解和對大尺度渦直接數值求解,該方法求解精度較高,消耗資源比DNS 方法少；鮑龍［12］采用LES 方法對不含轉向架的ICE2和CRH380A 型高速列車在復線隧道內行駛時的外部繞流進行了數值模擬,得到了列車繞流的瞬時速度及壓力云圖。RANS方法通過將N-S方程進行時間平均,將非定常的湍流問題轉化為一個定常的問題進行研究,該方法可以降低時間和空間的分辨率,減少對計算系統的需求并能獲得符合工程要求的計算結果；趙晶［13］基于雷諾平均N-S 方程及兩方程紊流模型,對CRH2型動車組過隧道時的空氣動力學問題進行了研究。DES 方法在湍流附面層內采用RANS 方法而在其它區域采用LES方法,既節省計算成本而且計算結果也比較令人滿意,但在建立模型時處理不當會引起模型的應力損耗。為此,Spalart 等人［14］提出了延遲脫體渦算法（Delayed Detached Eddy Simulation,DDES）,即在DES 計算中加入參數延遲控制,從而有效解決DES 方法容易引起應力損耗的問題,逐漸在列車外部繞流的數值模擬中得到廣泛應用。

因此,本文結合目前國內外研究現狀及存在的問題,基于延遲脫體渦算法和滑移網格技術,建立CRH380A 型高速列車含有轉向架的三維可壓縮瞬態仿真模型,模擬研究高速列車通過隧道時的氣動力、速度場和表面壓力3 大繞流特性的變化規律,以期為高速列車相關結構的強度評估和設計提供較為可靠的數據參考。

1 仿真模型的建立

1.1 延遲脫體渦算法

本文采用的DDES算法是對Spalart 等［14］于1997年提出的脫體渦算法的改進,即通過在邊界層內進行參數延遲控制,從而最大程度地降低DES算法引起的應力損耗。

DDES 算法的基礎是Menter 于1994年提出的剪切應力輸運（SST）k-ω湍流模型方程［15］,即

式中：ρ為流體密度；k為湍流運動的湍動能；t為時間；Ui為沿i方向的平均流速分量；xi為i方向的位移；Pk為湍流應力；μ為流體動力黏度系數；μt為渦黏系數；ω為湍流比耗散率；F1為混合函數；β*,σk,γ,β,σw和σw2均為模型常數,不同計算條件對應不同的取值。

混合函數F1的定義式為

其中,

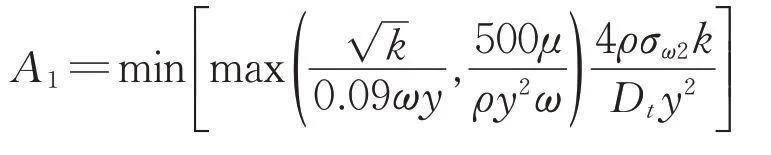
式中：y為近壁面最短的距離；Dt為交叉擴散項。

延遲脫體渦模擬算法的核心是將k方程式（1）中的耗散項（βρkω）修改為

其中,

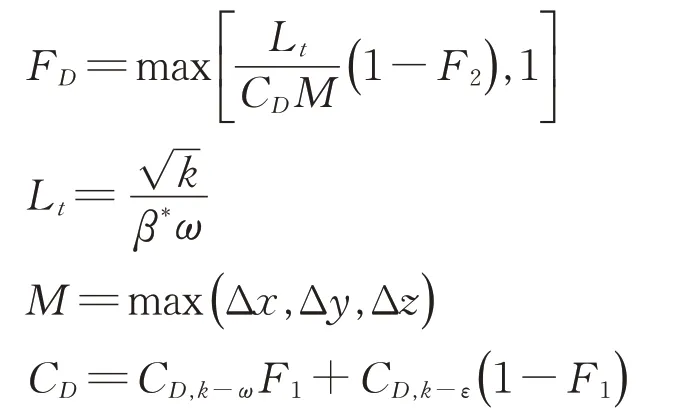
式中：M為網格中心到相鄰單元中心距離中最大的一個；CD,CD,k-ω,CD,k-ε均為模型常數；F2為另一混合函數；z為z方向的位移。

混合函數F2的定義式為

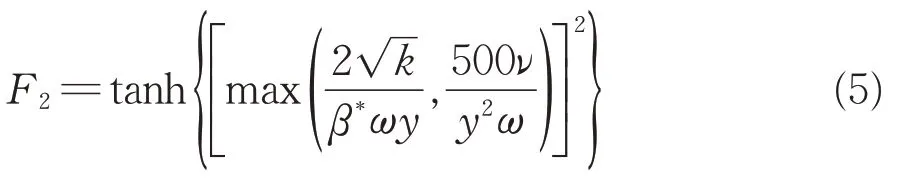
式中：ν為流體運動黏度系數。

在延遲脫體渦算法中：若FD= 1,則采用RANS模型計算；若FDES＞1,則采用LES模型求解。如果令F2= 0,則為原始的脫體渦算法。已有文獻表明［16］,在原始的脫體渦算法中,模型系數CD采用0.65 是最優值；而在延遲脫體渦模擬算法中,模型系數CD,k-ω=0.78,CD,k-ε=0.61。

1.2 滑移網格

基于滑移網格技術實現數值模擬中列車與隧道之間的相對運動。如圖1所示,將計算域分為區域1 和區域2 兩部分,區域1 為列車所在空間網格,區域2 為隧道內列車以外的空間網格。2 個區域獨立劃分網格,相鄰的網格則形成1個交界面；計算過程中,區域1 和區域2 的流場信息通過這一交界面進行交換。以區域1中的單元Ⅰ為例,單元Ⅰ的信息通過交界面a-f和f-b傳遞到區域2 中的單元Ⅴ和Ⅵ；其他單元信息交換與此類似,從而實現流場的瞬態數值模擬。

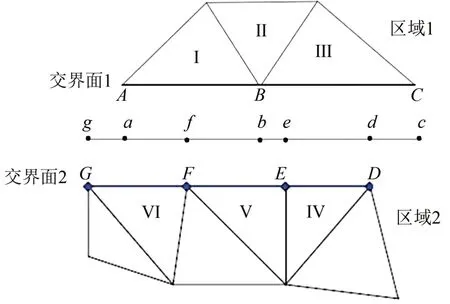
圖1 滑移網格示意圖

1.3 仿真模型及定解條件

列車模型基于高速動車組CRH380A的1/25縮比簡化模型,包括1 節頭車和1 節尾車（含司機室）,頭車的2 個轉向架采用簡化轉向架模型,尾車轉向架采用相對真實的轉向架模型,采用如圖2所示。列車模型長度ltr=1.58 m。

隧道模型參考京滬高速鐵路大斷面隧道［17］,半徑為6.87 m,橫斷面面積為100 m2,雙軌線間距為5 m ,列車斷面積的阻塞比為0.12。隧道長度ltu是列車長度的5 倍,即ltu=5ltr,從而盡可能準確地捕捉列車實際受到的氣動特性。

整個計算域的幾何模型及邊界條件如圖3所示,圖中H代表列車高度,作為特征長度。計算域包括隧道域、隧道出入口的空氣域和列車周圍的移動域；隧道壁面、列車表面邊界均設定為無滑移壁面,其余邊界條件均設定為壓力遠場。流場信息則通過將隧道空氣域與列車移動域的邊界設定為交界邊界來傳遞。整個計算域的離散方式采用六面體網格,并在車體流場處進行網格加密,同時在轉向架和車身表面處的位置采用邊界層網格,如圖4所示；隧道域的網格尺寸（方形網格邊長）為6.8 mm,列車移動域的網格尺寸為3.4 mm,設置邊界層內的網格增長率（網格尺寸的變化率）小于1.3,邊界層外的網格增長率小于等于2。

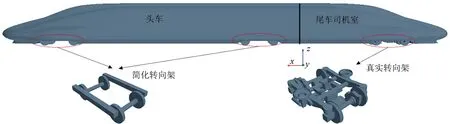
圖2 基于CRH380A的簡化列車模型及其轉向架模型

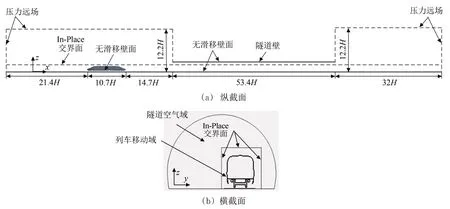
圖3 幾何模型及邊界條件

圖4 縱截面的計算網格

根據相關文獻［18-19］,當Ma2ltu/ltr?1（Ma為馬赫數,Ma=Ui/c,c為聲速）時,在模擬計算列車的繞流時必須考慮列車進出隧道時引起的空氣可壓縮性。基于此,建立基于延遲脫體渦算法的三維可壓縮非穩態仿真模型。根據Sutherland 公式,理想氣體的動力黏度系數μ計算公式為

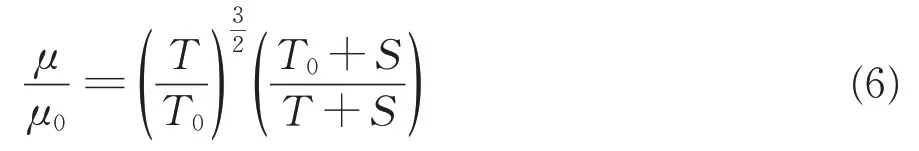
式中：S為Sutherland常數,本文取111 K；T0為參考溫度,其值為293 K；μ0為參考溫度下的動力黏度系數,其值為1.79×10-5Pa·s。

計算流場的初始化：設置壓力遠場U∞=0；列車以25 m·s-1的速度運動,以此模擬列車進出隧道的過程；計算初始,隧道入口與列車相距約是列車長度的1.5 倍,超過文獻［12］中給定的隧道入口與列車相距20～30 m,將有利于促進湍流的充分發展；時間步長設定為0.000 1 s。依據列車25 m·s-1的運行速度,列車與隧道剛接觸的時刻為t1*=t×Vtrltr= 1.38 s,列車剛全部進入隧道的時間為t2*= 2.38 s,列車尾部與隧道入口相距列車長度的2倍在t3*=4.38 s。

2 氣動力

根據列車阻力主要來源于列車的頭尾壓差阻力,為了便于分析,將列車劃分為3個部分：頭車Headbody、尾車Tailbody 和車底Others,其中車底包括列車底部所有結構,轉向架及設備艙、設備艙底板、排障器底板）。

2.1 氣動阻力

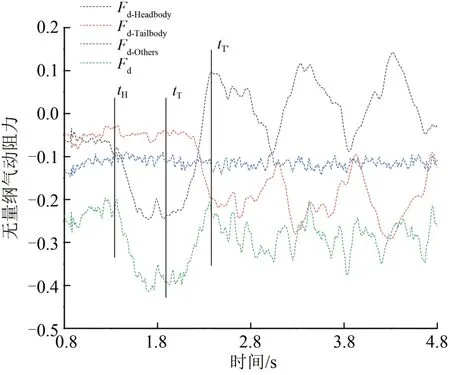
圖5 列車進入隧道過程中氣動阻力隨時間的變化曲線

列車進入隧道過程中氣動阻力隨時間的變化曲線如圖5所示。圖中：tH為頭車到達隧道口的時間點；tT’為車尾剛駛入隧道的時間點；tT為車尾完全進入隧道的時間點；Fd-Head,Fd-Tail,Fd-Others,Fd分別為頭車、尾車、車底和整車的氣動阻力。由圖5可看出：列車頭部剛駛入隧道時,頭車的氣動阻力突然增加,整車的氣動阻力也隨之驟升；當車頭完全進入隧道時,頭車的氣動阻力也達到最大；當尾車剛駛入隧道時,頭車的氣動阻力逐漸降低,整車的氣動阻力也隨之減少,尾車的氣動阻力逐漸增大；當尾車全部剛剛進入隧道時,尾車的氣動阻力驟然再次增加；當列車全部駛入隧道內時,尾車與頭車的氣動阻力呈現出相反相位的氣動波。

2.2 氣動升力

列車進入隧道過程中氣動升力隨時間的變化曲線如圖6所示,圖中,Fr-Head,Fr-Tail,Fr-Others,Fr分別為頭車、尾車、車底和整車的氣動升力。由圖6看出：在頭車剛進入隧道時,列車3個部分的氣動升力均無明顯變化；隨著列車的不斷進入,大約在尾車剛駛入隧道時,列車3個部分的氣動升力均明顯升高；而當尾車全部剛剛進入隧道時,列車3個部分的氣動升力無較大變化并且呈周期性變化；當列車全部駛入隧道內時,頭車和尾車分的氣動升力均為正,這有利于減小輪軌力,而車底的氣動升力為負,將列車壓向軌道。

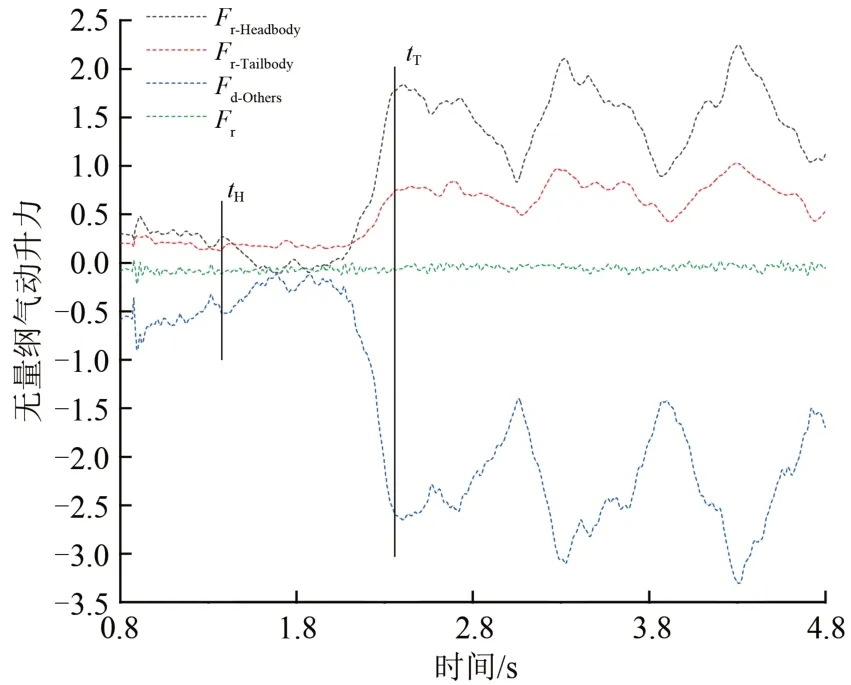
圖6 列車進入隧道過程中氣動升力隨時間變化曲線

2.3 氣動側向力

列車進入隧道的過程中氣動側向力隨時間的變化曲線如圖7所示,圖中Fs-Head,Fs-Tail,Fs-Others,Fs分別為頭車、尾車分、車底和整車的氣動升力。由圖7看出：車底的氣動側向力無明顯變化,保持在0 上下小幅波動；頭車和尾車的氣動側向力變化趨勢基本一致,頭車的波動幅度和數值均比尾車大；在尾車將要進入隧道時,頭車和尾車的氣動側向力突然增大,且均為正值,表明氣動側向力使得列車被壓向靠近隧道的一側。

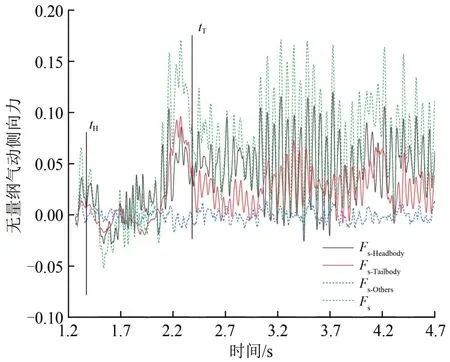
圖7 列車進入隧道過程中氣動側向力隨時間變化曲線

3 速度場

為了觀察列車通過隧道整個過程中車下流場的變化規律,在列車下方距離軌面z=-0.025 m 的高度上選取4 個橫斷面,其位置分別為距車頭x1=7.49 m,x2=16.49 m,x3=26.00 m 和x4=36.49 m,在每個橫斷面上沿車寬方向的位置設置3～7 個測點,測點分布在y=±2.25 m 之內,共21 個測點,編號為Lat 1—Lat 19,Lat 40,Lat 41,Lat 42,詳細如圖8所示,通過設定,使得這些測點相對于列車的位置始終不變。由于在列車高速運動前提下,測點的速度變化比較劇烈,所以采用移動平均方法對測點的速度數據進行處理,處理時將時期數（用于求平均數的數據量）設定為100。

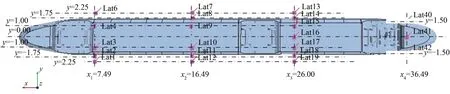
圖8 車下測點位置（單位：m）

3.1 縱向速度分量

在列車進入隧道過程中不同測點的無量綱速度縱向分量vx隨時間的變化曲線如圖9所示,由圖可得如下結論。

（1）在y=±2.25 m 線上,列車兩側對稱測點的速度縱向分量變化趨勢一致；頭車測點Lat 1 和Lat 6 的速度縱向分量,在頭車進入隧道時急劇增加,之后隨著頭車不斷進入隧道,其值基本無變化；另外3個斷面上測點的速度縱向分量,在頭車到達隧道時開始減小并且流動方向逐漸反向,當尾車進入隧道口時基本保持不變,在尾車進入隧道口時隧道與車身側墻之間形成回流區。

（2）在y=±1.75 m 線上,各個測點的速度縱向分量變化趨勢基本一致；當頭車進入隧道時各測點的速度縱向分量逐漸減小但波動幅度增大；當尾車進入隧道時速度縱向分量近似在同一水平波動；處于對稱位置的lat 8 測點,受隧道影響顯著,其速度縱向分量變化相比lat 11測點更明顯。

（3）在y=±1.00 m 線上,除了Lat 15 之外其它測點的速度縱向分量均有所降低,所有測點的速度流向未發生變化；位于靠近設備艙位置的測點Lat 9 和Lat 10,受隧道效應影響顯著,速度縱向分量降低更明顯,而其他測點速度縱向分量波動較為明顯。

3.2 橫向速度分量

在列車進入隧道過程中不同測點的無量綱速度橫向分量vy隨時間的變化曲線如圖10所示,由圖可得如下結論。

在y=2.25 m 線上,Lat 6 測點的橫向速度分量在列車駛入隧道后明顯減少,而Lat 13測點卻有一定程度升高；而在y=-2.25 m 線上,各個測點的速度基本無變化。

在y=1.75 m 線上,測點的橫向速度分量略微高于y=-1.75 m 線上的測點；在列車進入隧道過程中,隧道效應對各個測點沒有造成明顯的影響。

4 列車表面壓力分布

高速列車表面壓力分布情況是高速列車通過隧道時受到的氣動效應的直接體現。為此,在列車靠近隧道壁的一側,選取列車側面、車身裙板和列車底部分別布置測點,分析高速列車通過隧道時其表面的壓力分布。

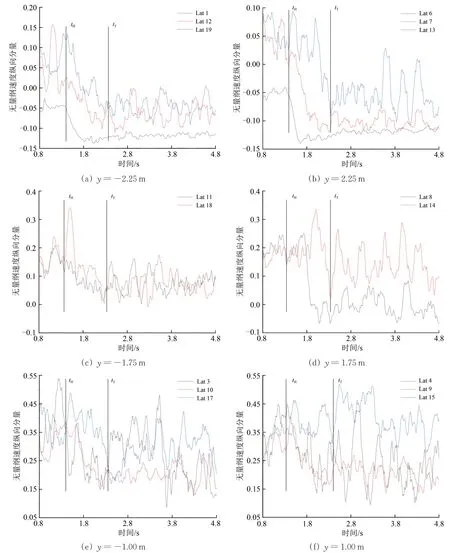
圖9 列車進入隧道過程中不同測點無量綱速度縱向分量vx隨時間變化曲線

4.1 列車側面壓力分布

列車側面上,在高度z=1.00 m、橫向位置分別為x=1.7,7.5,11.5,15.0,23.5,36.5 m 處布置6個測點,如圖11所示。

在列車進入隧道過程中列車側面各測點壓力隨時間的變化曲線如圖12所示,因S2與S3測點的變化規律十分接近,故未繪制S3 測點的壓力變化曲線。由圖可知：當頭車到達隧道口時,5 個測點的壓力都突然增大,由負壓上升為正壓,其中頭車的2個測點S0和S1的增幅最大,其它測點增幅較小；當頭車進入隧道之后,各個測點的壓力開始下降,直到尾車完全進入隧道時才停止下降；此后,壓力基本在負壓范圍內呈現周期性波動,處于尾流區的S5測點具有更強烈的波動特征。

4.2 列車裙板表面壓力分布

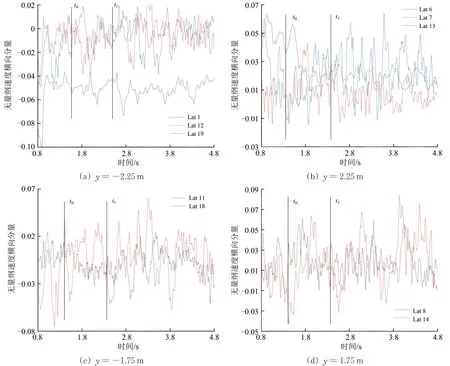
圖10 列車進入隧道過程中不同測點無量綱速度橫向分量vy隨時間變化曲線.

圖11 車身側面測點布置

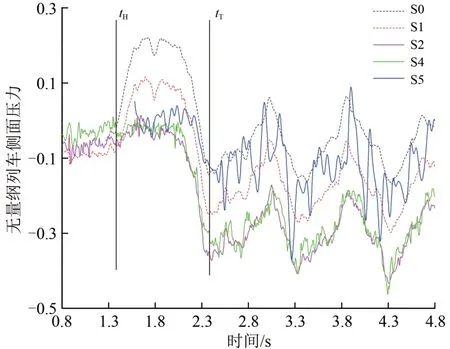
圖12 列車進入隧道過程中不同測點的壓力隨時間變化曲線

在靠近隧道壁一側的車身裙板上,在高度z=0.63 m、橫向位置分別為x=1.7,7.5,11.5,15.0,23.5,36.5 m 處布置8 個測點,如圖13所示。

在列車進入隧道過程中裙板各測點壓力（含頭車4 個測點的壓力標準差以及車身及尾車4 個測點的壓力標準差）隨時間的變化曲線如圖14所示,由圖可知：頭車測點的負壓呈現先減小后增加的趨勢,當尾車完全進入隧道時,壓力停止增加,此后各個測點的壓力維持在較高幅值波動變化；位于車身和尾車的4 個測點負壓在列車到達隧道口時開始大幅增加,在列車尾部到達隧道口時停止大幅增加,此后隨著列車的前進,各個測點的壓力維持在較高幅值波動變化；與列車未駛入隧道相比,列車駛入隧道之后頭車4 個測點的壓力標準差明顯減小。

4.3 列車底部表面壓力分布

在列車底部,即y=0 線上,選取7 個斷面x=1.7,7.5,11.5,15.0,23.5,36.5 m 處,每個斷面上布置1～3 個測點,共15 個測點,如圖15所示。

圖13 裙板測點位置

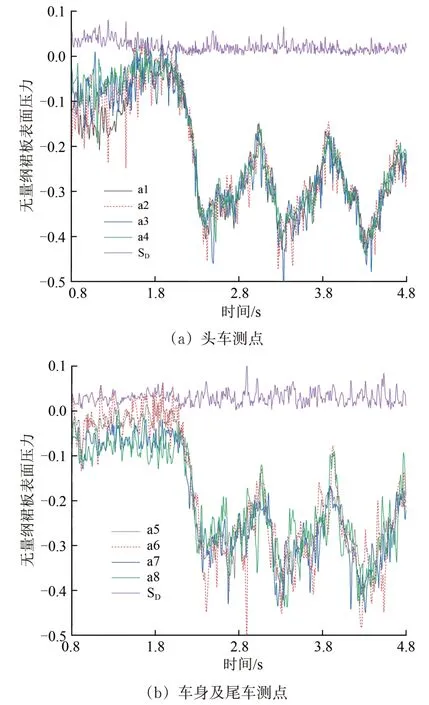
圖14 列車進入隧道過程中裙板各測點壓力隨時間變化曲線

在列車進入隧道過程中列車底部各測點壓力隨時間的變化曲線如圖16所示（為了便于分析,本文僅給出e1、e2、e4、e10、e13 和e15 這6 個測點的壓力變化）。由圖可知：這6 個測點的變化趨勢具有相似性,列車剛進入隧道時測點的負壓值出現略微的下降,之后隨著列車的不斷進入測點的負壓繼續下降,大約在尾車開始進入隧道時壓力值迅速增加并在尾車完全進入隧道時停止增加,當列車完全進入隧道之后測點保持較高的負壓水平上下波動；當列車完全進入隧道之后,6 個測點中,e15的壓力水平明顯低于其他測點,而e4的壓力最高且呈現出同時存在低頻振動和高頻振動的復雜波動。

圖15 車下測點位置

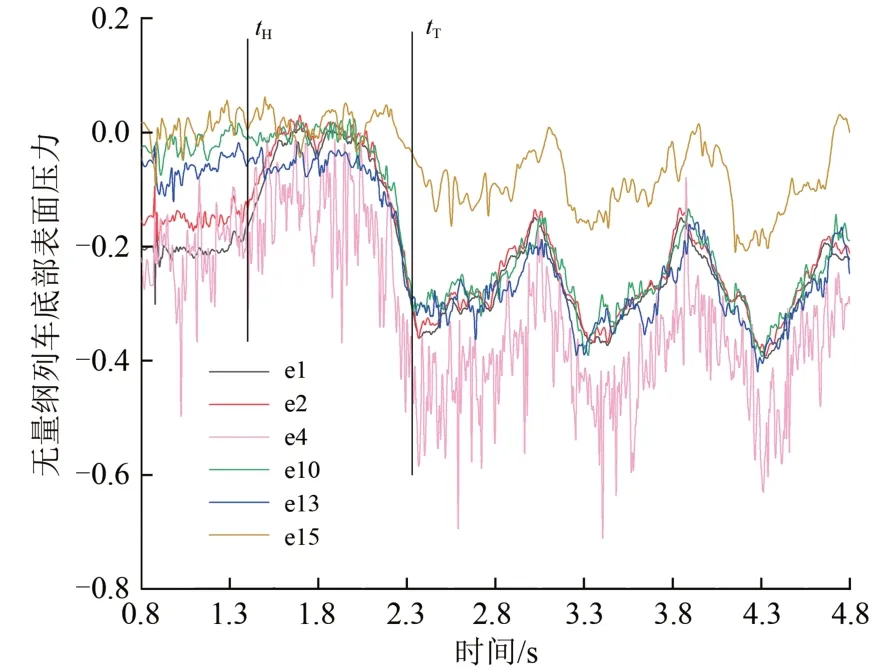
圖16 列車進入隧道過程中列車底部各測點壓力隨時間變化曲線

5 結 論

（1）延遲脫體渦算法能較好地捕捉列車通過隧道時的氣動特性；列車頭部剛與隧道接觸時,氣動阻力迅速升高并在車頭完全進入隧道時達到最大值；當尾車全部剛剛進入隧道時氣動升力和側向力驟然增加；當列車全部駛入隧道內后,氣動力的波動幅值均明顯升高；這均會對列車的平穩性和舒適性產生一定影響。

（2）在列車頭部剛與隧道接觸時,列車下方兩側的速度縱向分量會急劇增加,位于靠近設備艙位置的速度縱向分量會顯著降低；當尾車剛與隧道接觸時,隧道內壁與列車側面之間的流場會出現回流區；而這會對隧道中的人身安全及設施安全產生不良效果。

（3）列車通過隧道時,列車側面壓力整體上呈現先增大后減小、最后維持周期性波動的趨勢,處于尾流區的車尾部位具有更強烈的波動特征；列車裙板和車底的表面壓力整體上均呈現出先減小后增加、最后維持在較高幅值波動的趨勢。這會對列車相關結構的疲勞強度產生不利影響。