梯級(jí)潰壩洪水洪峰增強(qiáng)機(jī)制1)

黃 燦 劉青泉 王曉亮

(北京理工大學(xué)宇航學(xué)院力學(xué)系,北京 100081)

引言

我國(guó)水電資源豐富,當(dāng)前已經(jīng)建成各種類(lèi)型的水庫(kù)接近10 萬(wàn)座[1],西南地區(qū)的許多大型河流,如金沙江、大渡河等都已經(jīng)形成了梯級(jí)水庫(kù)布局[2],一旦發(fā)生梯級(jí)潰決,將誘發(fā)大型潰壩洪澇災(zāi)害,對(duì)下游沿岸的生產(chǎn)和生活帶來(lái)極大的影響.另一方面,地震災(zāi)害活動(dòng)經(jīng)常誘發(fā)滑坡形成堰塞壩和堰塞湖,其穩(wěn)定性和安全性存在極大的風(fēng)險(xiǎn),也將帶來(lái)梯級(jí)潰決風(fēng)險(xiǎn),如2018 年的白格堰塞體[3].因此研究梯級(jí)潰決洪水演進(jìn)過(guò)程及其機(jī)理對(duì)維護(hù)梯級(jí)水庫(kù)安全運(yùn)行具有重要意義.

近年來(lái)梯級(jí)潰決洪水過(guò)程受到了較大的關(guān)注,研究集中在室內(nèi)實(shí)驗(yàn)和數(shù)值模擬兩方面.Xue 等[4]開(kāi)展了比較系統(tǒng)的室內(nèi)梯級(jí)潰決室內(nèi)實(shí)驗(yàn),主要探討了壩間距、庫(kù)容比對(duì)下游水庫(kù)水流洪峰的影響.Niu等[5]在斜槽中堆積了梯形大壩,研究了梯級(jí)大壩潰決形式和潰壩水流的傳播過(guò)程.Chen 等[6]通過(guò)實(shí)驗(yàn)研究了潰壩水流對(duì)下游壩體的沖擊力作用,指出針對(duì)下游不同庫(kù)容存在3 種沖擊模式,并給出了作用力擬合公式.大量的工作集中在數(shù)值模擬方面,主要可以分為水文方法、淺水動(dòng)力學(xué)模擬,以及三維Navier-Stokes 方程模擬.趙雪瑩等[7]使用經(jīng)驗(yàn)公式研究了貴陽(yáng)柏山?花溪梯級(jí)水庫(kù)發(fā)生梯級(jí)潰決的洪水演進(jìn),分析了梯級(jí)水庫(kù)群不同水位組合總計(jì)4 種情況,誘發(fā)潰壩洪水對(duì)下游的影響,并指出降低庫(kù)水位將有效減輕潰壩洪水對(duì)下游影響.賀同坤等[8]使用Mike11 軟件模擬了瀾滄江中游五個(gè)水庫(kù)組成的梯級(jí)庫(kù)的特大洪水演進(jìn)過(guò)程,指出當(dāng)發(fā)生一萬(wàn)年一遇洪水時(shí),漫灣和景洪兩個(gè)水庫(kù)的最高水位接近壩頂.劉慶紅等[9]模擬了特定河流的梯級(jí)水庫(kù)群的連鎖響應(yīng)以及向下游演進(jìn)的過(guò)程.黃衛(wèi)等[10]建立了梯級(jí)大壩潰決洪水過(guò)程的淺水動(dòng)力學(xué)模型,研究了不同組合情況下梯級(jí)潰決洪水演進(jìn)過(guò)程,指出梯級(jí)潰決洪峰存在增強(qiáng)機(jī)制.隨后Cao 等[11]進(jìn)一步使用水沙耦合模型研究指出梯級(jí)潰決誘發(fā)洪水將更具威脅,當(dāng)前的單壩潰決預(yù)案需要改進(jìn).Wang 等[12]比較了淺水動(dòng)力學(xué)模型和Boussinesq 模型模擬梯級(jí)潰決洪水的傳播的爬升過(guò)程,并指出Boussinesq 在相對(duì)較大水深處能給出更加精確的解.Zhou 等[13]使用VOF 方法和湍流模型研究了梯級(jí)潰決洪水過(guò)程.Luo 等[14]用近年來(lái)快速發(fā)展的無(wú)網(wǎng)格粒子方法(SPH)模擬了梯級(jí)潰決過(guò)程,將潰壩洪水效應(yīng)分為高速?zèng)_擊區(qū)和傳壓區(qū)兩個(gè)過(guò)程.李仟[15]研究了梯級(jí)土石壩潰決洪水的演進(jìn)和調(diào)洪過(guò)程,對(duì)下游洪水過(guò)程進(jìn)行了風(fēng)險(xiǎn)分析.袁岳[16]用RANS 模型和標(biāo)準(zhǔn)k–ε 模型模擬了不同坡角,壩間距及庫(kù)容比對(duì)潰決過(guò)程的影響,比較了單級(jí)潰決和梯級(jí)潰決不同潰決模式下水流流動(dòng)特點(diǎn).趙丹[17]研究上寺水庫(kù)大壩潰決的流量過(guò)程,并對(duì)當(dāng)前使用的常見(jiàn)模型模擬精度進(jìn)行了比較.

綜上所述,當(dāng)前對(duì)梯級(jí)潰決開(kāi)展了一些機(jī)理性實(shí)驗(yàn)研究和各種不同類(lèi)型的數(shù)值模擬,主要研究潰壩洪水過(guò)程,大部分都指出了梯級(jí)潰決相對(duì)單壩潰決存在增強(qiáng)現(xiàn)象,但是對(duì)梯級(jí)潰決洪峰增強(qiáng)機(jī)制缺乏基本的物理和力學(xué)解釋,特別是缺少質(zhì)量和能量轉(zhuǎn)化如何增強(qiáng)梯級(jí)潰決洪水過(guò)程的認(rèn)識(shí).本文使用淺水動(dòng)力學(xué)方法研究梯級(jí)潰決洪水過(guò)程,從梯級(jí)潰決上游來(lái)水對(duì)下游水庫(kù)的質(zhì)量和能量補(bǔ)充及分布方面入手,對(duì)梯級(jí)潰決洪峰增強(qiáng)機(jī)制進(jìn)行一些探索,并給出了一個(gè)射流水塔單壩潰決模式等效梯級(jí)潰決洪水過(guò)程.

1 控制方程與數(shù)值方法

土石壩的潰決過(guò)程十分復(fù)雜,涉及水流過(guò)程、泥沙沖刷以及壩體坍塌及其復(fù)雜的流固耦合問(wèn)題[18-22],本文主要研究壩體潰決誘發(fā)的洪水過(guò)程,因此對(duì)壩體坍塌采取瞬間潰決的模式進(jìn)行處理.雖然潰壩過(guò)程在局部水流結(jié)構(gòu)復(fù)雜,但是潰壩洪水演化的過(guò)程基本發(fā)生在很長(zhǎng)的河道,其水平尺度相比于水流的垂向尺度大得多,因此滿(mǎn)足淺水動(dòng)力學(xué)的基本假設(shè)[23-24].本節(jié)主要給出潰壩洪水的基本控制方程和數(shù)值方法,并通過(guò)幾個(gè)經(jīng)典案例驗(yàn)證數(shù)值模型的有效性.

1.1 控制方程

由于潰壩洪水過(guò)程的水平尺度遠(yuǎn)大于垂向尺度,并且本文對(duì)潰壩過(guò)程采取瞬間潰決的方式處理,因此潰壩洪水演化過(guò)程可以用淺水動(dòng)力學(xué)方程描述

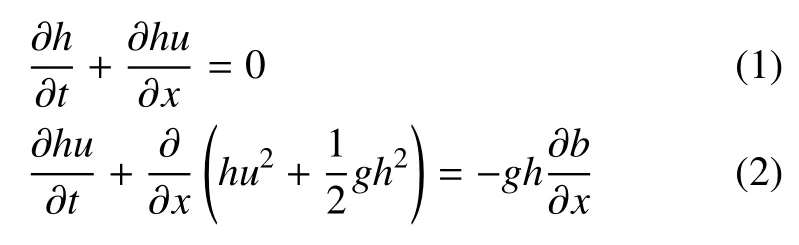
其中,h和u分別表示水深和水平方向的垂向平均速度,g和b則分別表示重力加速度和地形高程.本文考慮大尺度洪水演進(jìn)過(guò)程和機(jī)理研究,因此忽略摩擦作用.

1.2 數(shù)值方法

淺水動(dòng)力學(xué)模型(1)和(2)是一組非線(xiàn)性雙曲型偏微分方程,其典型的特征是會(huì)出現(xiàn)水躍(激波),同時(shí)由于源項(xiàng)的作用,存在一個(gè)平衡解,即所謂Well-Balance 條件,另一方面實(shí)際問(wèn)題經(jīng)常遇到一側(cè)水深為零的情況,即所謂的干濕條件,因此這套控制方程的求解算法需要具備至少3 個(gè)特征,捕捉激波、滿(mǎn)足Well-Balance 條件,以及捕捉干濕邊界.過(guò)去十年在非線(xiàn)性雙曲守恒律的高分辨率數(shù)值格式方面取得了重要的進(jìn)展[25-27],本文綜合考慮了這3 方面的需求,結(jié)合近期淺水動(dòng)力學(xué)計(jì)算方法的進(jìn)展,融合了Kurganov的Riemann 解[28-30]和Audusse[31-32]的單元插值模式,構(gòu)造了一套淺水動(dòng)力學(xué)模型的離散格式.

首先將控制方程寫(xiě)成守恒形式,如式(3)所示

其中,U=(h,hu)T,F=(hu,hu2+gh2/2)T,s(U)=[0,?gh(?b/?x)]T.

采用一套滿(mǎn)足 Well-Balance 行為的有限體積法[31]對(duì)守恒方程(3)進(jìn)行離散,得到以下的離散格式,如式(4)所示

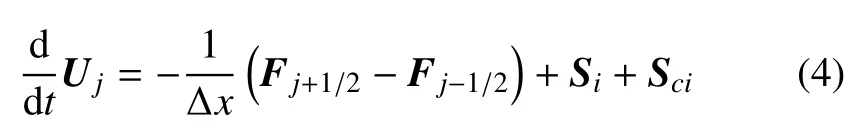
其中Uj=(hj,qj)T為第j個(gè)單元的單元平均值,數(shù)值通量Fj+1/2的構(gòu)造采用MUSCL 方法[33],如式(5)所示

這里Uj+(1/2)?=(hj+(1/2)?,hj+(1/2)?uj,r)T,Uj+(1/2)+=(hj+(1/2)+,hj+(1/2)+uj+1,l)T.

采用滿(mǎn)足 Well-Balance 特性的插值方式構(gòu)造hj+(1/2)?和hj+(1/2)+,其中hj+(1/2)?=max(0,hj,r+bj,r?bj+1/2),hj+(1/2)+=max(0,hj+1,l+bj+1,l?bj+1/2),這里bj+1/2=max(bj,r,bj+1,l).所有的單元左右重構(gòu)值均采用二階MUSCL 方法構(gòu)造,并采用Minmod 限制器抑制虛假振蕩[34].

這里的Riemann 近似求解器可以采用任意形式的Riemann 求解器,本文考慮計(jì)算穩(wěn)定性,采用了近年來(lái)新發(fā)展的Kurganov 近似解[30].源項(xiàng)部分包括兩項(xiàng),其表達(dá)式分別如式(6)和式(7)所示

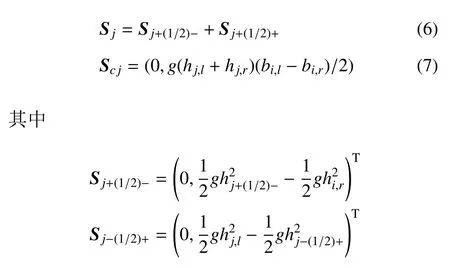
時(shí)間離散采取二階Runge-Kutta 方法.

1.3 模型驗(yàn)證

本節(jié)采取兩個(gè)典型的例子驗(yàn)證1.2 中算法的有效性,兩個(gè)例子分別是潰壩問(wèn)題和Well-Balance 問(wèn)題,將給出兩個(gè)問(wèn)題的數(shù)值解和解析解的比較.

1.3.1 潰壩問(wèn)題簡(jiǎn)單波解

經(jīng)典潰壩問(wèn)題以一側(cè)為水,另一側(cè)無(wú)水為初始情況,瞬間抽除擋板后的水流運(yùn)動(dòng)演化過(guò)程.該過(guò)程存在解析解,稱(chēng)為簡(jiǎn)單波解[35].設(shè)計(jì)初始水深h0=10 m,x=0 為初始擋板位置,本例的解析解為h=(h0/9)(2 ?x/ct)2,u=2(c+x/t)/3,其中波速,流量Q=hu.

圖1 給出了時(shí)刻0.072 1 s 的水深h和流量Q的計(jì)算結(jié)果,可以發(fā)現(xiàn)計(jì)算結(jié)果和解析解基本吻合.

圖1 潰壩問(wèn)題在時(shí)刻0.0721 s 的水深和流量分布,數(shù)值解和理論解的比較,H 為水位,Q 為流量Fig.1 Height and discharge distribution of dam break flow at 0.0721 s,the red dashed line and blue symbols are analytical and numerical solutions respectively,where H is water depth,and Q is discharge

1.3.2 Well-Balance 行為

地形變化情況的淺水動(dòng)力學(xué)方程存在一個(gè)穩(wěn)態(tài)解結(jié)構(gòu),即h+b=const,q=0,即在流量為0 的時(shí)候,自由表面為常數(shù).這個(gè)結(jié)構(gòu)在數(shù)值模型中需要保持,稱(chēng)為Well-Balance 問(wèn)題.本例給出了底部為一個(gè)高度為5 m 的近似拋物線(xiàn)凸起,自由水面高程為10 m 例子的數(shù)值模擬.圖2 給出了本例在時(shí)刻10.093 2 s 的數(shù)值解,可以發(fā)現(xiàn)自由水面高程保持常數(shù),同時(shí)流量在凸起位置處為很小的值,約10?5m2/s 量級(jí),這在后續(xù)的工程計(jì)算中是可以接受的.

圖2 Well-Balance 問(wèn)題的驗(yàn)證,H+b 為水位,Q 為流量,綠色虛線(xiàn)為底床高程Fig.2 Verification for Well-Balance behavior over a bump denoted by red dashed line,where H+b is free surface elevation,and Q is discharge

2 梯級(jí)壩潰決洪水演進(jìn)

梯級(jí)水庫(kù)是當(dāng)前水資源開(kāi)發(fā)利用中的常見(jiàn)模式,上游壩體的潰決往往又會(huì)導(dǎo)致下游壩體的潰決,其流動(dòng)過(guò)程更為復(fù)雜.針對(duì)這種梯級(jí)水庫(kù)開(kāi)發(fā)模式,本文模擬了典型的兩個(gè)梯級(jí)壩連續(xù)潰決的洪水演進(jìn)過(guò)程,重點(diǎn)分析梯級(jí)潰決引發(fā)的洪峰增強(qiáng)現(xiàn)象.

2.1 梯級(jí)壩潰決洪水演進(jìn)過(guò)程

如圖3 所示,在坡度為α 的河道上,上下游存在兩個(gè)壩體,其間距為L(zhǎng),兩個(gè)壩體圍成了兩個(gè)水庫(kù),其庫(kù)容高度分別為h1和h2,梯級(jí)潰決過(guò)程是,首先上游壩體突然潰決,水流往下游傳播,下游壩前水位超過(guò)壩體高度后下游壩體瞬間潰決,形成潰壩洪水往下游傳播.主要關(guān)注潰壩洪水的演進(jìn)過(guò)程及其對(duì)下游的影響,因此在下游處設(shè)置兩個(gè)測(cè)點(diǎn)P1和P2,測(cè)點(diǎn)P1距離下游水庫(kù)的距離為L(zhǎng)1,測(cè)點(diǎn)P2距離測(cè)點(diǎn)P1的距離為L(zhǎng)2.

圖3 梯級(jí)潰決問(wèn)題描述以及測(cè)點(diǎn)Fig.3 Cascade dam-break model and detection points P1 and P2

這里模擬一個(gè)梯級(jí)潰決的洪水演進(jìn)過(guò)程,其中h1=h2=100 m,L=1000 m,L1=L2=1000 m,α=12?,圖4 給出了4 個(gè)典型時(shí)刻的水位高程分布.0 s 時(shí)刻隨著上游壩體的潰決,上游水庫(kù)水體向下傾瀉而出,向下游水庫(kù)傳播,約10 s 左右上游潰壩洪水傳到下游水庫(kù),如圖4(a)所示;形成一個(gè)穩(wěn)定的向下游水庫(kù)傳播的水躍(激波),如圖4(b)所示;水躍傳播到下游壩體時(shí)候下游壩體潰決,從而形成洪水往下游傳播,如圖4(c)所示,部分上游水體和下游水庫(kù)合在一起宛如一個(gè)水塔為下游洪水提供充足的質(zhì)量和動(dòng)量來(lái)源;最終如圖4(d)所示,洪水繼續(xù)往下游傳播,直至消亡.

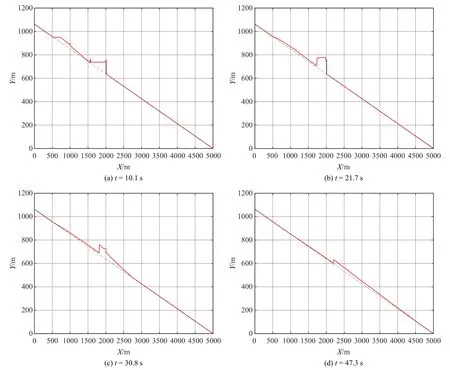
圖4 典型梯級(jí)潰決洪水演進(jìn)過(guò)程水位分布Fig.4 Water elevation distribution at four typical times of cascade dam break flow

2.2 梯級(jí)壩連續(xù)潰決洪峰增強(qiáng)現(xiàn)象

為研究梯級(jí)潰決下游河道的洪峰演化和增強(qiáng)現(xiàn)象,選取兩個(gè)參考測(cè)點(diǎn)P1和P2,其距離下游壩體分別為1000 m 和2000 m,考察其洪水演進(jìn)時(shí)間歷程,結(jié)果如圖5 所示.為比較,同時(shí)給出了另外3 種潰決模式,分別是上游和下游壩體單獨(dú)潰決模式,以及將上游水體體積加載在下游水庫(kù)的單壩潰決模式(等體積潰決模式).圖5(a) 表明梯級(jí)潰決模式在P1測(cè)點(diǎn)的最高水位能達(dá)到23.56 m,下游單壩潰決模式在P1測(cè)點(diǎn)的最高洪峰為10.33 m,上游單壩潰決模式在P1測(cè)點(diǎn)的最高水位為7.50 m,而等體積潰決模式在P1測(cè)點(diǎn)的最高水位為17.19 m.綜合來(lái)看,梯級(jí)潰決模式在P1誘發(fā)的洪峰大大超過(guò)單板潰決洪峰,還超過(guò)上游下游單個(gè)潰決模式的最高洪峰之和,也超過(guò)等體積潰決模式的最高洪峰,在P2測(cè)點(diǎn)也有類(lèi)似的規(guī)律.這論證了梯級(jí)潰決模式存在洪峰增強(qiáng)現(xiàn)象,上游水庫(kù)不僅對(duì)下游水庫(kù)進(jìn)行了質(zhì)量補(bǔ)充,還進(jìn)行了大量的能量補(bǔ)充,但是這種質(zhì)量和能量如何進(jìn)行補(bǔ)充的,又是如何分布的,是梯級(jí)潰決洪水演進(jìn)和洪峰增強(qiáng)的關(guān)鍵.

3 梯級(jí)壩潰決洪峰增強(qiáng)機(jī)制

第2 節(jié)的計(jì)算分析表明梯級(jí)潰決誘發(fā)洪水洪峰超過(guò)單個(gè)壩體單獨(dú)潰決洪峰的總和,也超過(guò)將上游體積放到下游后等效的所謂等體積潰決模式的洪峰,梯級(jí)潰決模式中,下游水庫(kù)實(shí)際上既從上游水庫(kù)的潰壩洪水繼承了部分質(zhì)量,而且繼承了部分能量,但是質(zhì)量和能量是如何補(bǔ)充和分布的應(yīng)當(dāng)是梯級(jí)潰決洪峰增強(qiáng)的關(guān)鍵因素.本節(jié)重點(diǎn)分析梯級(jí)潰決的質(zhì)量和能量轉(zhuǎn)化過(guò)程,并給出幾個(gè)關(guān)鍵機(jī)制的分析.

圖5 四種潰決模式下游測(cè)點(diǎn)P1(a)和P2(b)的洪水位時(shí)間演化,其中Cascade Mode 為梯級(jí)潰決模式,Downstream Mode 和Upstream Mode 分別為下游和上游單壩潰決模式,Single Equivalent Mode 表示等體積潰決模式Fig.5 Flood elevation evolution at detection points P1 (a)and P2 (b)for four dam break modes:cascade dam break mode,single downstream dam break mode,single upstream dam break mode,and single downstream dam break with full water mode

3.1 能量轉(zhuǎn)化機(jī)制

圖4 的梯級(jí)潰決洪水演化過(guò)程表明上游壩體潰決對(duì)下游水庫(kù)既增大了質(zhì)量又增大了能量,圖6 給出了下游壩體潰決瞬間的水深分布和速度分布,下游水庫(kù)形成了一個(gè)基本穩(wěn)定的梯形水塔,其自由面高程基本為常數(shù)(圖4(b)),由于底床為直線(xiàn)分布,因此水深為線(xiàn)性分布如圖6(a) 所示,其速度由后部至前部呈線(xiàn)性分布如圖6(b) 所示; 而后部實(shí)際拖了很長(zhǎng)的一段水流,其速度由尾部向前部逐漸增大,前后兩部分通過(guò)一個(gè)運(yùn)動(dòng)水躍(激波)連接.因此初步的分析表明上游潰壩洪水對(duì)下游潰壩的效應(yīng)體現(xiàn)在兩個(gè)方面,其一是增大了其質(zhì)量,其二是增大了其動(dòng)量,余下的水體質(zhì)量和動(dòng)量滯留在后部.以上機(jī)制表明可以考慮將梯級(jí)潰決誘發(fā)洪水過(guò)程簡(jiǎn)化成一個(gè)帶動(dòng)量的初始水體的單壩潰決情況處理.

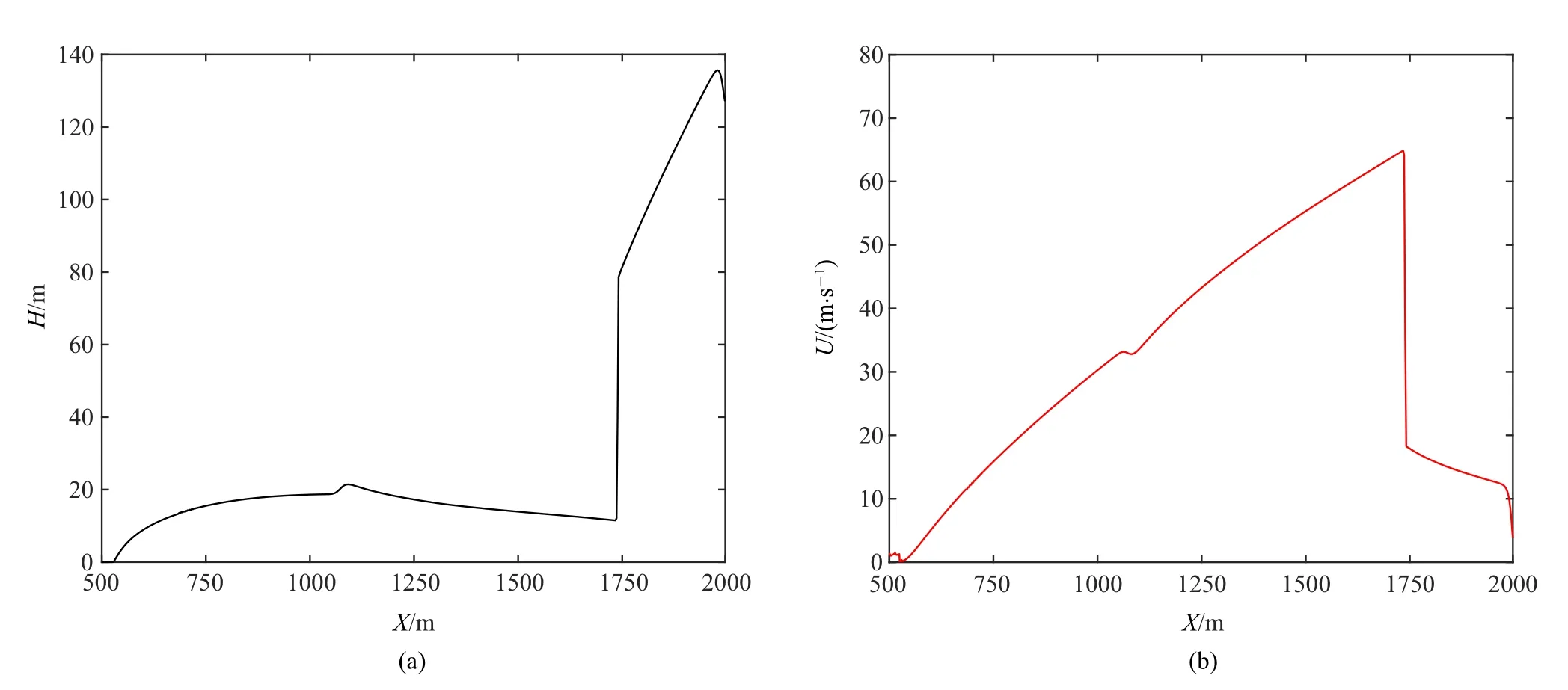
圖6 梯級(jí)潰決下游壩體潰決瞬間的高程(a)和速度分布(b)Fig.6 Depth(a)and velocity(b)distribution of flood when downstream dam breaks

3.2 “水塔”機(jī)制

由于下游壩體臨近潰決瞬間的結(jié)構(gòu)為前部集中分布的水體和后部拖了很長(zhǎng)距離的一段水體,前部宛如一個(gè)水塔,將梯級(jí)潰決過(guò)程等效成帶動(dòng)量水體的單壩潰決模式,稱(chēng)之為“水塔”機(jī)制,因此建立一個(gè)所謂“水塔”模型,即帶動(dòng)量水塔單壩潰決模型,如圖7 所示.水塔的質(zhì)量和速度和原始模型協(xié)調(diào)給定,如圖8 所示,其中自由表面高程為常數(shù),速度分布也考慮成常數(shù).“水塔”模型的潰決洪水過(guò)程如圖9 所示,將初始時(shí)刻協(xié)調(diào)后,可以發(fā)現(xiàn)測(cè)點(diǎn)P1和測(cè)點(diǎn)P2的洪峰高度均小于原始梯級(jí)潰決過(guò)程的在兩個(gè)測(cè)點(diǎn)的洪峰高程.因此“水塔”機(jī)制僅僅反映了一部分梯級(jí)潰決洪峰增強(qiáng)機(jī)理.

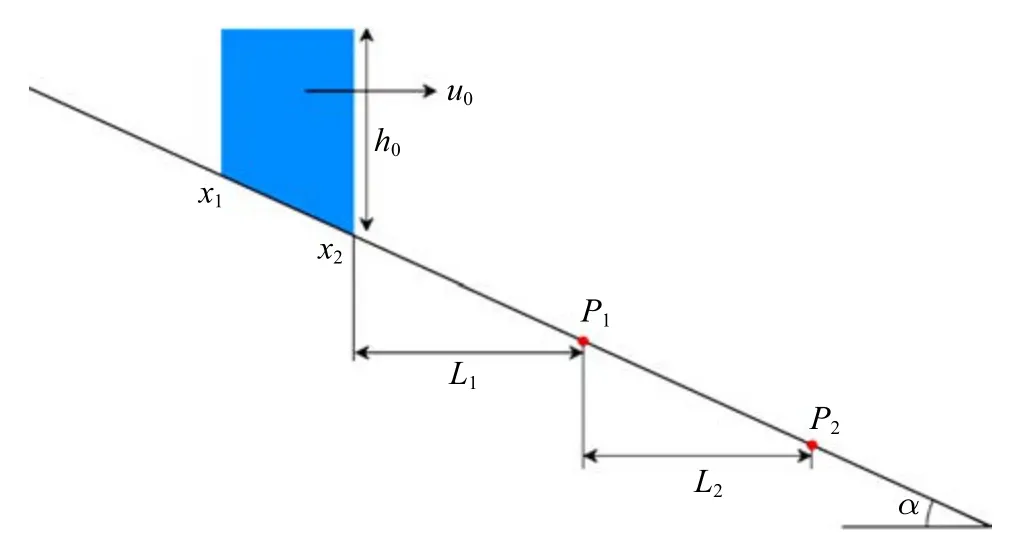
圖7 梯級(jí)潰決洪水演進(jìn)的水塔模型Fig.7 Water tower model of cascade dam break flow

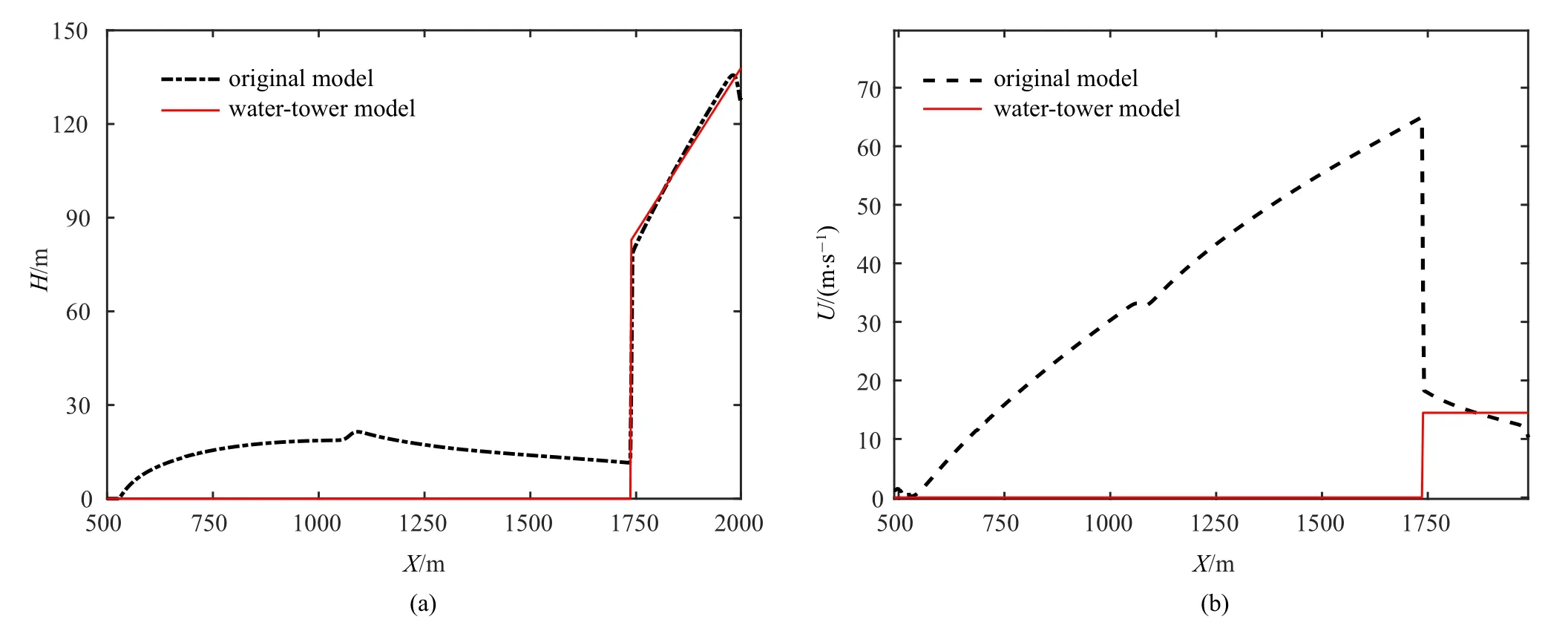
圖8 梯級(jí)潰決洪水演進(jìn)水塔模型的初始水深(a)和速度分布(b)Fig.8 Initial water depth(a)and velocity(b)of water tower model for cascade dam break flow

圖9 梯級(jí)潰決下游測(cè)點(diǎn)P1 (a)和P2 (b)洪水演進(jìn)過(guò)程的水塔模型預(yù)測(cè),虛線(xiàn)為原始模型計(jì)算結(jié)果,實(shí)線(xiàn)為水塔模型預(yù)測(cè)結(jié)果Fig.9 Prediction of flood level at detection positions P1 (a)and P2 (b)of cascade dam break flow by water tower model,dashed line is shallow water flow model prediction,and solid line represents water tower model prediction

3.3 “射流?水塔”機(jī)制

以上水塔模型低估了梯級(jí)潰決洪峰的能量,進(jìn)一步經(jīng)過(guò)計(jì)算分析,對(duì)于本例,前部水塔的質(zhì)量占總質(zhì)量的61.2%,動(dòng)量則占總動(dòng)量的37.7%,后部水體的動(dòng)量占據(jù)比例非常大,類(lèi)似一股射流作用,對(duì)前部水塔有很強(qiáng)的質(zhì)量、動(dòng)量補(bǔ)充作用,以維持洪峰的高度,稱(chēng)之為梯級(jí)潰決的“射流?水塔”機(jī)制.因此建立如圖10 所示的“射流?水塔”模型,射流為一股帶速度分布的等水深射流,而水塔則和水塔模型一致.射流的速度分布采取兩種模型,如圖11 所示,第一種為常數(shù)分布,第二種為線(xiàn)性分布,分別稱(chēng)為射流水塔模型和分布式射流水塔模型.兩種模型模擬的洪水演進(jìn)過(guò)程在測(cè)點(diǎn)P1和測(cè)點(diǎn)P2的洪峰演化如圖12 所示.結(jié)果表明射流水塔模型的預(yù)測(cè)結(jié)果明顯偏大,而分布式射流水塔模型的洪峰過(guò)程更加接近實(shí)際洪峰過(guò)程,但是依然存在一定的偏差.由此可知,分布式射流水塔模型相比于射流水塔模型、水塔模型以及單壩潰決洪峰疊加模式更能反映梯級(jí)潰決的洪水演進(jìn)過(guò)程.

圖10 梯級(jí)潰決洪水演進(jìn)過(guò)程的射流水塔模型Fig.10 Jet-water tower model for cascade dam break flow

圖11 梯級(jí)潰決射流水塔模型的水深(a)和速度分布(b),其中藍(lán)線(xiàn)虛線(xiàn)為射流水塔模型(JWT)的水深和速度分布,而紅線(xiàn)實(shí)線(xiàn)為分布式射流水塔模型(DJWT)的水深和速度分布,黑色點(diǎn)劃線(xiàn)是原始模型水深和速度分布Fig.11 Initial water depth(a)and velocity(b)of jet-water tower model for cascade dam break flow,blue dashed line,red solid line and black dash dot line represent water depth and velocity of jet-water tower model(JWT),distributed jet-water tower model(DJWT),and original shallow water model,respectively

4 分布式“射流?水塔”模型應(yīng)用

梯級(jí)潰決洪水演進(jìn)過(guò)程存在“射流?水塔”機(jī)制,一方面上游潰壩洪水增大下游庫(kù)容的質(zhì)量和動(dòng)量,另一方面殘余的水流構(gòu)成一個(gè)高速的射流在下游潰壩洪水演進(jìn)過(guò)程中不斷補(bǔ)充質(zhì)量和動(dòng)量,維持洪峰高度.第3 節(jié)總結(jié)了一個(gè)反映這種機(jī)制的分布式射流水塔模型,本節(jié)應(yīng)用該模型預(yù)測(cè)兩組接近實(shí)際尺度的梯級(jí)壩潰決洪峰,考察不同的庫(kù)容比和壩間距的影響,總共設(shè)計(jì)7 組算例,其中坡降tan α=0.1%,計(jì)算區(qū)域?yàn)?00 km,壩間距在100 km 量級(jí),在距離下游壩處100 km 和200 km 處分別選取測(cè)點(diǎn)P1和測(cè)點(diǎn)P2,分別考察洪峰水位和流量的演進(jìn)過(guò)程,同時(shí)選取原始淺水動(dòng)力學(xué)模型的計(jì)算結(jié)果作為比較對(duì)象,相關(guān)結(jié)果整理后如表1 和表2 所示.

圖12 梯級(jí)潰決下游測(cè)點(diǎn)P1 (a)和P2 (b)洪水演進(jìn)過(guò)程的兩類(lèi)射流水塔模型預(yù)測(cè),虛線(xiàn)為原始模型計(jì)算結(jié)果,藍(lán)線(xiàn)虛線(xiàn)為射流水塔模型(JWT)預(yù)測(cè)結(jié)果,紅線(xiàn)實(shí)線(xiàn)為分布式射流水塔模型(DJWT)預(yù)測(cè)結(jié)果,黑色點(diǎn)劃線(xiàn)為淺水動(dòng)力學(xué)模擬結(jié)果Fig.12 Prediction of flood level at detection positions P1 (a)and P2 (b)of cascade dam break flow by jet-water tower model(JWT)in blue dashed line and distributed jet-water tower model(DJWT)in red solid line,and black dash dot line is the shallow water model solution

表1 實(shí)際尺度梯級(jí)壩潰決洪峰水位預(yù)測(cè)Table 1 Peak flood elevation prediction of real-scale cascade dam break flow

表2 實(shí)際尺度梯級(jí)壩潰決洪峰流量預(yù)測(cè)Table 2 Peak flood discharge prediction of real-scale cascade dam break flow

總體而言,分布式射流水塔模型反映了梯級(jí)潰決的洪水峰值,其預(yù)測(cè)的洪峰值和原始模型預(yù)測(cè)的洪峰值基本吻合.對(duì)于間距為100 km 的兩個(gè)壩體,庫(kù)容比在0.6 ～1.2 的范圍內(nèi),下游100 km 處洪水峰值的預(yù)測(cè)值誤差在6%以?xún)?nèi),200 km 處洪峰的預(yù)測(cè)值誤差小于7%; 對(duì)于庫(kù)容比為1.0,間距在100 ～250 km范圍內(nèi)的梯級(jí)潰決過(guò)程,下游200 km 以?xún)?nèi),分布式射流水塔模型預(yù)測(cè)的洪峰誤差在15%以?xún)?nèi).對(duì)于下游100 km 處測(cè)點(diǎn),由表2 可知洪峰流量的預(yù)測(cè)值和淺水動(dòng)力學(xué)模型計(jì)算結(jié)果吻合較好,下游測(cè)點(diǎn)200 km的P2測(cè)點(diǎn),誤差隨著壩間距的增大而增大,這主要是由于潰決模式和洪水增強(qiáng)機(jī)理存在差異所致.

5 結(jié)論

針對(duì)梯級(jí)潰壩洪水演進(jìn)問(wèn)題,本文建立了一維淺水動(dòng)力學(xué)方程和數(shù)值模型,詳細(xì)研究了梯級(jí)潰的洪峰增強(qiáng)機(jī)制,并建立了一個(gè)梯級(jí)潰決洪水演進(jìn)的單壩潰決等效模型.主要結(jié)論如下:

(1)梯級(jí)潰決的洪水過(guò)程存在增強(qiáng)機(jī)制,下游洪峰不僅超過(guò)單壩潰決洪峰,而且超過(guò)兩個(gè)單壩潰決的峰值之和,以及所謂等體積潰決模式的洪峰.

(2) 梯級(jí)潰決的洪峰增強(qiáng)由射流水塔機(jī)制控制,上游潰決誘發(fā)的洪水不僅增大下游水庫(kù)的質(zhì)量和動(dòng)量,形成“水塔”,而且在尾部殘留一個(gè)動(dòng)量較大的射流,穩(wěn)定和維持下游潰決后“水塔”的質(zhì)量和動(dòng)量.

(3)以梯級(jí)潰決洪水演進(jìn)增強(qiáng)的射流?水塔機(jī)制為基礎(chǔ),建立了一個(gè)等效的射流水塔單壩潰決等效模型,預(yù)測(cè)結(jié)果基本能夠反映梯級(jí)潰決下游洪峰演化過(guò)程,對(duì)實(shí)際百公里量級(jí)間距的梯級(jí)潰決洪峰過(guò)程預(yù)測(cè)良好.

梯級(jí)潰壩洪水過(guò)程十分復(fù)雜,潰決模式和增強(qiáng)機(jī)制方面依然還有待進(jìn)一步研究,如在可沖刷河床情況下梯級(jí)潰決的洪峰增強(qiáng)機(jī)制,此外本文提出的射流水塔模型是否存在解析/半解析的參數(shù)化模型.本文所建立的梯級(jí)潰決洪水過(guò)程的單壩潰決等效模型為實(shí)際梯級(jí)潰決洪峰過(guò)程提供了理論上的可能,但是如何將本模型和實(shí)際河道如金沙江及其支流的梯級(jí)壩關(guān)鍵參數(shù)對(duì)應(yīng)進(jìn)行安全評(píng)估還有很多實(shí)際因素需要考慮,如地形、河道截面和能量耗散.