結(jié)構(gòu)沖擊畸變問題的直接相似方法研究1)

王 帥 徐 緋,2) 代 震 劉小川 李肖成 楊磊峰 惠旭龍

?(西北工業(yè)大學(xué)航空學(xué)院計算力學(xué)與工程應(yīng)用研究所,西安 710072)

?(中國飛機強度研究所結(jié)構(gòu)沖擊動力學(xué)航空科技重點實驗室,西安 710065)

引言

沖擊現(xiàn)象廣泛存在,促使人們尋求更有效、經(jīng)濟、可靠的防護結(jié)構(gòu)[1-3].當(dāng)理論和數(shù)值研究受到限制,結(jié)構(gòu)沖擊的實驗測試則變得必不可少.在實驗設(shè)計中,結(jié)構(gòu)沖擊相似理論是備受青睞的研究領(lǐng)域,這主要在于通過小尺寸模型預(yù)測全尺寸結(jié)構(gòu)響應(yīng)的實驗具有經(jīng)濟成本低、實驗周期短、實驗環(huán)境易實現(xiàn)等明顯優(yōu)勢[4].經(jīng)典的沖擊相似理論已廣為人知,它通過單一的幾何比例因子聯(lián)系比例模型與原型的物理量,并被廣泛應(yīng)用于汽車、高鐵、船舶、飛機、核電站等工程結(jié)構(gòu)受沖擊的安全防護設(shè)計中[5-6].此外,Johnson[5,7]提出著名的損傷數(shù)Dn,用來測量沖擊結(jié)構(gòu)的損傷程度.趙亞溥[8-9]在損傷數(shù)Dn的基礎(chǔ)上,提出了考慮結(jié)構(gòu)幾何的響應(yīng)數(shù)Rn,被廣泛應(yīng)用于彈塑性結(jié)構(gòu)的沖擊動力響應(yīng)分析.這些無量綱數(shù)的提出,進一步擴充了經(jīng)典沖擊相似理論的基礎(chǔ).然而,當(dāng)考慮比例模型材料的應(yīng)變率敏感性效應(yīng)、屈服應(yīng)力、密度等不同于原型,以及考慮重力、斷裂效應(yīng)時,經(jīng)典的相似理論則會發(fā)生畸變[5-6,10-14].因此,有必要發(fā)展處理畸變問題的沖擊相似理論.

針對材料的畸變問題,Drazetic 等[15-19]使用一組基于VSG(initial impact velocity-dynamic flow stressimpact massG)量綱分析的無量綱數(shù),在幾何比例因子的基礎(chǔ)上,增加了速度比例因子,并通過一種間接相似方法修正比例模型的沖擊速度或沖擊質(zhì)量,進而補償材料應(yīng)變率敏感性效應(yīng)引起的畸變.然而這種間接相似方法,存在需要預(yù)先測試比例模型響應(yīng)信息的困難,因而并不實用.Oshiro 和Alves[20]進一步使用冪律形式的Norton-Hoff 本構(gòu)方程,發(fā)展了一種直接相似方法,無需測試結(jié)構(gòu)響應(yīng)信息即可獲得修正沖擊速度的比例因子,克服了間接相似法的缺陷.Mazzariol 等[21]在VSG 體系中增加了結(jié)構(gòu)質(zhì)量的無量綱數(shù)以及密度比例因子,并使用一種新的直接相似方法修正沖擊速度,進而補償應(yīng)變率敏感性效應(yīng)以及屈服應(yīng)力和密度不同時的不同材料引起的畸變.Oshiro 等[22-24]對船舶碰撞與擱淺的大型結(jié)構(gòu)工程沖擊問題,使用1/100 的比例模型試驗,驗證了VSG 不同材料畸變理論的有效性以及其對復(fù)雜問題的適應(yīng)能力.Mazzariol 等[25-26]在VSG 的基礎(chǔ)上,對不同材料的畸變問題,研究了同時考慮幾何畸變的相似途徑.張振華等[27-32]針對船艦結(jié)構(gòu)加筋板受爆炸載荷,研究了考慮流固耦合、應(yīng)變率敏感性效應(yīng)、不同材料引起的畸變問題,通過VSG 間接相似方法修正沖擊速度,驗證了VSG 理論對加筋板結(jié)構(gòu)受爆炸沖擊載荷的有效性.姜正榮等[33-34]對單層網(wǎng)殼結(jié)構(gòu),考慮了應(yīng)變率敏感性效應(yīng)引起的畸變以及重力引起的畸變,并提出通過附加質(zhì)量修正結(jié)構(gòu)密度的縮放技術(shù),為大型結(jié)構(gòu)的相似試驗提供了新的技術(shù)手段.魏德敏和胡晨曦[35]使用一種部分相似的技術(shù),發(fā)展了修正密度的方法,結(jié)合間接相似方法改變結(jié)構(gòu)質(zhì)量和沖擊質(zhì)量,處理應(yīng)變率敏感性效應(yīng)引起的畸變.蘇子星和何繼業(yè)[36]基于Cowper-Symonds 方程,修正了VSG 不同材料畸變問題中沖擊速度的計算方法.Sadeghi 等[37-41]使用一組連續(xù)介質(zhì)力學(xué)的輸運方程,提出了有限相似(finite similitude) 理論,從方程分析的角度驗證了VSG 不同材料畸變體系的合理性,并同時考慮了材料的應(yīng)變硬化效應(yīng)以及斷裂的相似性問題.王帥等[42]提出了DLV(density-length-velocity)量綱分析體系替代VSG 體系,從無量綱數(shù)、響應(yīng)方程和相似分析的角度進一步擴展了應(yīng)用范圍,并修正沖擊速度和密度以補償不同材料引起的畸變.

本工作采用VSG 沖擊畸變相似理論體系和最佳平方逼近方法,推導(dǎo)了不同材料引起的畸變問題的一種直接相似方法,研究了本構(gòu)模型中材料參數(shù)對流動屈服應(yīng)力動態(tài)相似關(guān)系的影響,以期為結(jié)構(gòu)沖擊安全防護設(shè)計中使用比例模型試驗提供一種處理畸變問題的直接相似技術(shù).

1 直接相似方法

1.1 傳統(tǒng)的相似方法

對于不同材料引起的畸變問題,通常使用一組基于VSG[16,20-21,43]或DLV[42]的量綱分析體系來解決,它們具有相同的比例因子.在此,本工作使用較為簡潔的DLV 體系簡要回顧結(jié)構(gòu)沖擊問題的相似律.該理論由一組基于密度(ρ)、長度(L)、速度(V)為基本量的無量綱數(shù)構(gòu)成,其中幾個主要的無量綱數(shù)為:應(yīng)力(σ),Πσ=ρV2/σ;應(yīng)變(ε),Πε=ε;角度(θ),Πθ=θ;應(yīng)變率(),Π=L/V; 時間(t),Πt=tV/L; 位移(δ),Πδ=δ/L;質(zhì)量(M),ΠM=M/ρL3.與此對應(yīng),該理論由一組基于幾何比例因子β=Lm/Lp、速度比例因子βV=Vm/Vp、密度比例因子βρ=ρm/ρp為基礎(chǔ)的比例關(guān)系表達(dá)物理量的相似關(guān)系,其中幾個主要的比例因子為:應(yīng)力βσ=;應(yīng)變βε=1;角度βθ=1;應(yīng)變率=βV/β;時間βt=β/βV;位移βδ=β;質(zhì)量βM=βρβ3.式中,下標(biāo)m 和p 分別代表比例模型和原型.

基于這組無量綱數(shù)和比例因子,在進行比例模型試驗時,由于幾何比例因子、密度比例因子是已知的,因而應(yīng)用該理論的關(guān)鍵技術(shù)在于通過本構(gòu)方程合理地計算速度比例因子,進而修正比例模型的沖擊速度.在VSG 體系中,通過對本構(gòu)方程σd=f()應(yīng)用比例關(guān)系來計算速度比例因子βV,進而修正比例模型的沖擊速度,補償不同材料引起的畸變.需強調(diào)的是,應(yīng)變率敏感性效應(yīng)畸變已包含在不同材料畸變中,因而不再刻意區(qū)分.

早期的VSG 相似理論研究[16-19,27-31,33-36],需預(yù)先通過試驗或某種技術(shù)手段獲取比例模型或原型的平均應(yīng)變率信息,進而作為已知條件計算修正沖擊速度的速度比例因子.Oshiro 和Alves[16]對應(yīng)變率敏感性效應(yīng)引起的畸變,定義速度因子為

為克服間接相似方法的缺陷,Oshiro 和Alves[20]對應(yīng)變率敏感性效應(yīng)引起的畸變,通過使用特殊形式的Norton-Hoff 冪律本構(gòu)方程,定義速度因子為

式中,σ0為屈服應(yīng)力,為σ0對應(yīng)的參考應(yīng)變率,q為應(yīng)變率敏感性特征參數(shù).顯然,該方法定義的速度因子βV,僅由幾何比例因子β 及材料參數(shù)q確定,無需預(yù)先測試結(jié)構(gòu)的任何響應(yīng)信息,是一種直接相似方法.然而,對于其他形式的本構(gòu)方程,不能直接獲得速度比例因子,通用性有限.

Mazzariol 等[21]考慮材料應(yīng)變率敏感性效應(yīng)、屈服應(yīng)力、密度不同引起的不同材料的畸變,定義速度因子為

式中,βσ0=(σ0)m/(σ0)p是屈服應(yīng)力比例因子,βvisco=fm()/fp(β/βV) 是本構(gòu)方程中應(yīng)變率敏感性黏性項的比例因子.對直接相似,文獻中針對Johnson-Cook 本構(gòu)模型簡單設(shè)定=1 s?1從而簡化獲取結(jié)構(gòu)平均應(yīng)變率的間接過程.然而,這種對平均應(yīng)變率的簡單設(shè)定,忽略了結(jié)構(gòu)應(yīng)變率在沖擊過程中隨時間和空間變化的動態(tài)特性,因而不能反映結(jié)構(gòu)沖擊的動態(tài)相似性質(zhì).

此外,式(2)、式(3)定義的傳統(tǒng)的直接相似方法,缺乏本構(gòu)方程材料參數(shù)對動態(tài)相似關(guān)系影響的探究.對文獻[34-35,42]中提出的修正密度來改變結(jié)構(gòu)質(zhì)量和沖擊質(zhì)量的方法,也未考慮.

1.2 直接相似方法的推導(dǎo)

本文對VSG 體系中計算修正沖擊速度或修正密度的比例因子的關(guān)鍵技術(shù)問題,提出一種基于最佳平方逼近關(guān)系的直接相似法,可適用于任何形式的應(yīng)變率敏感性的本構(gòu)方程σd=f().

在VSG 相似理論下,比例模型和原型的流動屈服應(yīng)力和應(yīng)變率關(guān)系為

當(dāng)使用比例模型的流動屈服應(yīng)力預(yù)測原型時,將式(5)代入式(4)中,預(yù)測值為

考慮在沖擊過程中,動態(tài)屈服應(yīng)力和應(yīng)變率隨位置和運動時間而變化.因而,對于沖擊問題的相似性,應(yīng)包含這種動態(tài)過程的連續(xù)相似.這就要求比例模型預(yù)測的流動屈服應(yīng)力與原型的流動屈服應(yīng)力在應(yīng)變率區(qū)間上應(yīng)始終重合.顯然,對大多數(shù)由試驗擬合的本構(gòu)方程,實現(xiàn)這種嚴(yán)格意義的精確重合并不現(xiàn)實.對此,可采用函數(shù)逼近的方法近似描述這個動態(tài)相似過程,使得在一個連續(xù)的應(yīng)變率區(qū)間上它們的平均誤差最小.因而可在應(yīng)變率區(qū)間上,通過預(yù)測動態(tài)屈服應(yīng)力與原型動態(tài)屈服應(yīng)力(σd)p的最佳平方逼近,來描述這種動態(tài)相似過程.

圖1 不同應(yīng)變率區(qū)間對流動屈服應(yīng)力?應(yīng)變率曲線預(yù)測結(jié)果的比較Fig.1 Comparison of the prediction results for the function curves between the flow yield stress and the strain rate curves by the different strain rate intervals

以上分析表明,當(dāng)應(yīng)變率積分區(qū)間均值的數(shù)量級與結(jié)構(gòu)原型相同或相近時,可獲得最佳逼近效果.因而,使用粗略的應(yīng)變率數(shù)量級區(qū)間替代原型精確的真實應(yīng)變率區(qū)間的方法是合理的.為此,我們對取為0 s?1,取為結(jié)構(gòu)原型應(yīng)變率均值所在數(shù)量級,如10 s?1,100 s?1,200 s?1,500 s?1,1000 s?1,5000 s?1,1.0×104s?1等.此時,在比例模型測試前,一個簡單粗糙的原型應(yīng)變率數(shù)量級估計,就可以使用式(7)直接求出速度比例因子.相比文獻[37]對應(yīng)變率使用一個非常寬的固定窗口[0 s?1,1.0×104s?1]的做法,本文提出的應(yīng)變率數(shù)量級區(qū)間的方法,明確了應(yīng)變率區(qū)間數(shù)量級對最佳逼近效果的影響,更為合理.

此外,式(7) 還可以進一步擴展.針對文獻提出的修正材料密度的方法,可在式(7) 中預(yù)先固定βV,將βρ作為未知量,從而求出最佳逼近時的新的密度比例因子,進而修正比例模型結(jié)構(gòu)質(zhì)量和沖擊質(zhì)量.本文只討論修正模型沖擊速度的方法.

1.3 考慮材料參數(shù)后的直接相似方法

當(dāng)使用式(7)定義的直接相似方法時,為獲得比例模型預(yù)測流動屈服應(yīng)力與原型流動屈服應(yīng)力(σd)p的最佳逼近效果,還需考慮具體材料參數(shù)的影響,從而使得這種動態(tài)相似性始終存在.

下面取3 種經(jīng)典的材料本構(gòu)模型,來展示直接相似法在考慮材料參數(shù)后的應(yīng)用過程.

(1)當(dāng)使用Norton-Hoff 本構(gòu),根據(jù)式(7)得到

此時,除了比例因子β,最佳逼近關(guān)系受βq,和βσ0/βρ的影響.

為進一步導(dǎo)出考慮材料參數(shù)后的最佳逼近條件,假設(shè)βq=1,由式(9)得到

當(dāng)比例模型與原型材料相同,則比例模型材料應(yīng)變率敏感性特征參數(shù)q、參考應(yīng)變率、屈服應(yīng)力σ0、密度ρ 與原型相同.對相同材料,退化為=βq/(q?2),即式(2)給出的速度修正因子.此時,無論q,,σ0,ρ 取何值,比例模型與原型始終是理想動態(tài)相似的.

當(dāng)比例模型與原型材料不同,則比例模型材料的應(yīng)變率敏感性特征參數(shù)q、參考應(yīng)變率、屈服應(yīng)力σ0、密度ρ 與原型不同.對不同材料,式(10)分析表明,比例模型材料的參考應(yīng)變率、屈服應(yīng)力σ0、密度ρ 取值對最佳逼近效果沒有影響,而應(yīng)變率敏感性特征參數(shù)q具有主導(dǎo)作用.當(dāng)比例模型q取值越接近原型,最佳逼近效果越接近理想相似情況,對原型逼近程度越好.

對于比例模型材料參數(shù)q與原型不同的情況,我們通過具體例子進一步分析.對原型,根據(jù)參考文獻[22] 給定的1008 軟鋼的Norton-Hoff 本構(gòu),取=0.031 s?1,q=0.08.對比例模型,=0.031 s?1,q為0.02～0.30.此外,假定βσ0/βρ=1,β=1/10,應(yīng)變率區(qū)間為0～1000 s?1,從而使用式(9) 求解.圖2顯示了比例模型材料參數(shù)q的變化對無量綱預(yù)測流動屈服應(yīng)力()p/(σ0)p與預(yù)測應(yīng)變率關(guān)系曲線的影響.

圖2 材料參數(shù)q 對預(yù)測流動屈服應(yīng)力?預(yù)測應(yīng)變率曲線的影響(Norton-Hoff 本構(gòu))Fig.2 The influence of material parameter q for the function curves between the flow yield stress and the strain rate curves(Norton-Hoff equation)

從圖2 可見,當(dāng)比例模型參數(shù)q與原型接近時,逼近效果最佳,這與式(10)的分析結(jié)果完全一致.當(dāng)比例模型與原型參數(shù)q相差較大時,比例模型預(yù)測流動屈服應(yīng)力與原型流動屈服應(yīng)力的誤差明顯增大.可見,對使用不同材料的縮放試驗,選取參數(shù)q與原型接近的材料是縮放試驗成功進行的必要條件,這意味著比例模型需選用與原型具有相同應(yīng)變率硬化能力的材料.

(2) 當(dāng)使用Cowper-Symonds 本構(gòu),根據(jù)式(7)得到

此時,除比例因子β,最佳逼近關(guān)系受βP,βD和βσ0/βρ的影響.

為進一步從材料角度定義式(12)的動態(tài)相似關(guān)系,我們分析材料應(yīng)變率敏感性特征參數(shù)P、特征應(yīng)變率D(類似于Norton-Hoff 中參考應(yīng)變率)、屈服應(yīng)力σ、密度ρ 對()p和(σd)p動態(tài)逼近程度的影響.

對比例模型和原型,根據(jù)參考文獻[5] 給定的幾種典型金屬材料的Cowper-Symonds 本構(gòu)參數(shù),分別選取參數(shù)范圍:D從10～9000,P從2～10,βσ0/βρ從0.2～8.幾何比例因子β 為1/10,應(yīng)變率區(qū)間為0～1000 s?1,從而使用式(12) 求解.圖3 顯示了材料參數(shù)D,P,σ0,ρ 的變化對無量綱預(yù)測流動屈服應(yīng)力()p/(σ0)p與預(yù)測應(yīng)變率關(guān)系曲線的影響.

從圖3(a)和圖3(b)可見,當(dāng)比例模型與原型使用相同材料,無論特征應(yīng)變率D、應(yīng)變率敏感性特征參數(shù)P的取值如何變化,比例模型預(yù)測流動屈服應(yīng)力與原型流動屈服應(yīng)力都顯現(xiàn)出良好的一致性.此外,從圖3(a)還可看到,當(dāng)D取值由小變大,流動屈服應(yīng)力對應(yīng)變率越不敏感,而動態(tài)逼近效果基本不受影響;從圖3(b)還可看到,當(dāng)P取值越大,流動屈服應(yīng)力對應(yīng)變率越不敏感,動態(tài)逼近效果越好.從圖3(c)和圖3(d)可見,當(dāng)比例模型與原型使用不同材料時,不同的特征應(yīng)變率D均能獲得良好的動態(tài)逼近效果,而不同的應(yīng)變率敏感性特征參數(shù)P的動態(tài)逼近效果差異顯著.當(dāng)比例模型與原型參數(shù)P相差較大時,預(yù)測流動屈服應(yīng)力與原型流動屈服應(yīng)力兩者誤差明顯增大.此外,當(dāng)比例模型參數(shù)P大于原型,更容易獲得最佳逼近效果.從圖3(e)可見,比例模型材料參數(shù)σ0,ρ 的變化幾乎不影響比例模型與原型的動態(tài)相似性.以上分析表明,對于Cowper-Symonds 本構(gòu),當(dāng)比例模型選用與原型應(yīng)變率硬化能力相同的材料時,逼近效果最佳.此時,應(yīng)變率敏感性特征參數(shù)P起主導(dǎo)作用.

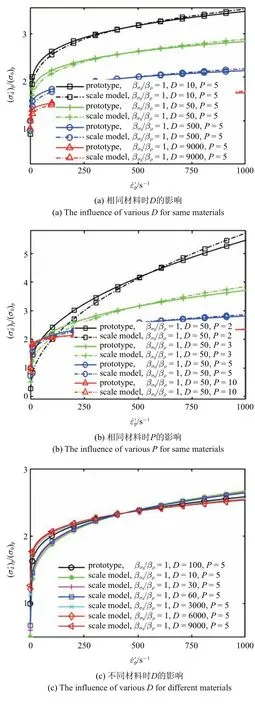
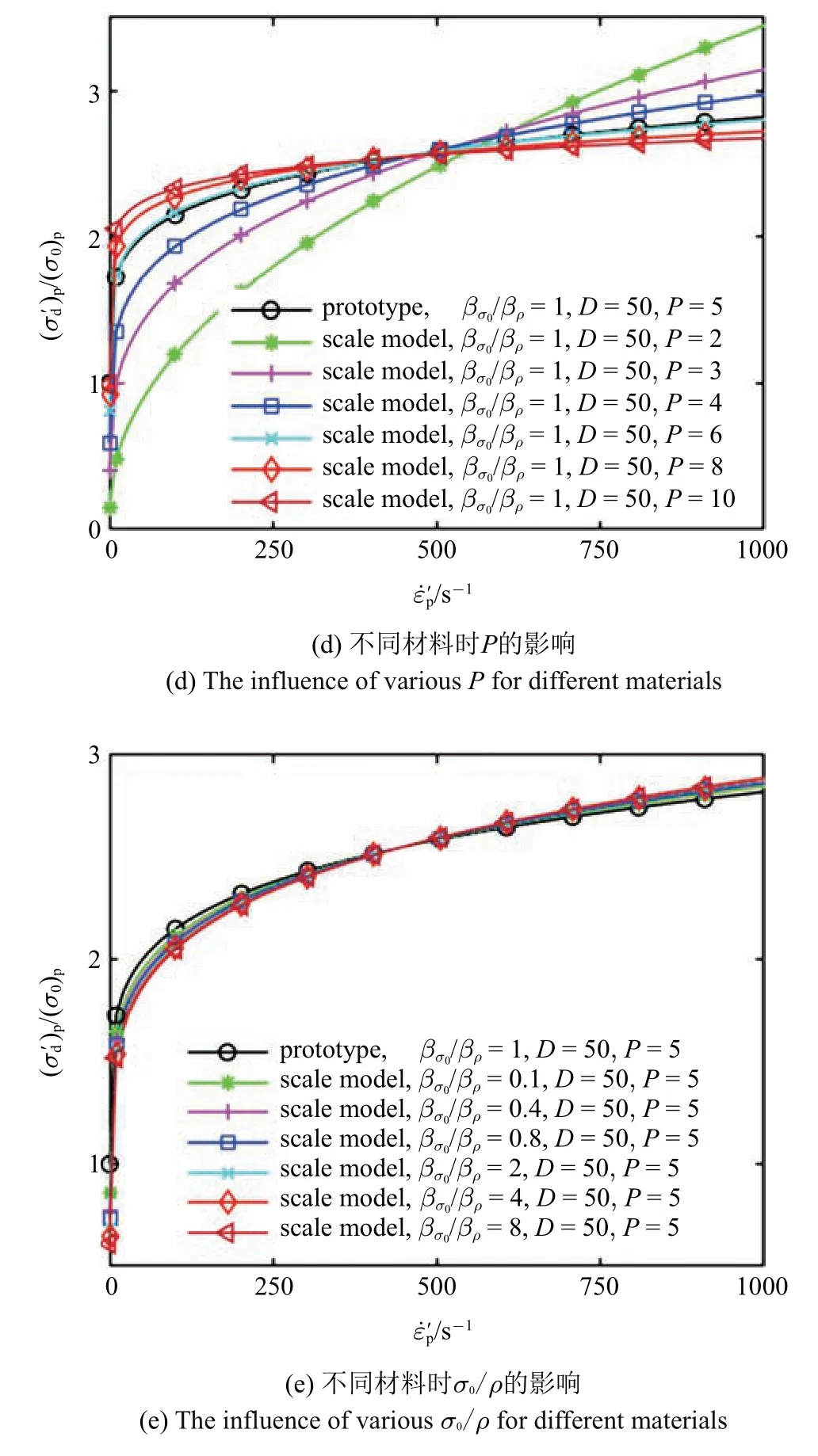
圖3 材料參數(shù)對預(yù)測流動屈服應(yīng)力?預(yù)測應(yīng)變率曲線的影響(Cowper-Symonds 本構(gòu))Fig.3 The influence of material parameters for the function curves between the flow yield stress and the strain rate curves(Cowper-Symonds equation)

(3) 當(dāng)使用簡化后的 Johnson-Cook 本構(gòu)模型(忽略應(yīng)變硬化效應(yīng)和溫度效應(yīng)),即σd=σ0[1 +,式中,C為應(yīng)變率敏感性特征參數(shù)、為參考應(yīng)變率參數(shù),通常設(shè)定為1 s?1.根據(jù)式(7)得到

此時,除比例因子β,最佳逼近關(guān)系受βC,,βσ0/βρ的影響.由于Johnson-Cook 本構(gòu)中參考應(yīng)變率一般取為1 s?1,因而得到=1.此時,只需關(guān)注變量βC和βσ0/βρ即可.對此,我們分析應(yīng)變率敏感性特征參數(shù)C、屈服應(yīng)力σ0、密度ρ 對()p和(σd)p動態(tài)逼近程度的影響.

對比例模型和原型,根據(jù)參考文獻[21] 給定的幾種典型金屬材料的Johnson-Cook 本構(gòu)參數(shù),分別選取參數(shù)范圍為:C為0.001～0.1,βσ0/βρ為0.2～8.幾何比例因子β 為1/10,應(yīng)變率區(qū)間為0～1000 s?1,從而使用式(14)求解.圖4 顯示了材料參數(shù)C,σ/ρ的變化對無量綱預(yù)測流動屈服應(yīng)力()p/(σ0)p與預(yù)測應(yīng)變率關(guān)系曲線的影響.

從圖4(a) 可見,當(dāng)比例模型與原型使用相同材料,無論應(yīng)變率敏感性特征參數(shù)C取值如何變化,比例模型預(yù)測流動屈服應(yīng)力與原型流動屈服應(yīng)力都顯現(xiàn)出良好的一致性.從圖4(b)可見,當(dāng)比例模型與原型使用不同材料,比例模型不同的應(yīng)變率敏感性特征參數(shù)C的取值對原型的動態(tài)逼近效果差異顯著.當(dāng)二者相差較大時,預(yù)測誤差明顯增大.此外,當(dāng)比例模型參數(shù)C的值大于原型時,更容易獲得最佳逼近.從圖4(c)可見,材料參數(shù)σ0、ρ 的變化幾乎不影響比例模型與原型的動態(tài)相似性.以上分析表明,當(dāng)比例模型選用與原型應(yīng)變率硬化能力相同的材料時,逼近效果最佳,此時參數(shù)C起主導(dǎo)作用.

圖4 材料參數(shù)對預(yù)測流動屈服應(yīng)力?預(yù)測應(yīng)變率曲線的影響(Johnson-Cook 本構(gòu))Fig.4 The influence of material parameters for the function curves between the flow yield stress and the strain rate curves(Johnson-Cook equation)

以上對3 種經(jīng)典材料本構(gòu)模型的定性分析表明,比例模型參考應(yīng)變率、屈服應(yīng)力、密度這些材料參數(shù)的變化對式(7) 定義的動態(tài)最佳逼近相似關(guān)系影響很小,而應(yīng)變率敏感性特征參數(shù)(對Norton-Hoff 為q,對Cowper-Symonds 為P,對Johnson-Cook 為C)影響較大.比例模型的應(yīng)變率敏感性特征參數(shù)越接近原型,即兩者具有相同的應(yīng)變率硬化能力,越容易獲得動態(tài)最佳逼近效果.

更一般地,對任何形式的本構(gòu)方程σd=f(),假定X為其應(yīng)變率敏感性特征參數(shù),那么式(7)在考慮這個主導(dǎo)性的材料因素后,可重新定義為

1.4 方法對比

為驗證直接相似方法的有效性,對比使用不同方法時比例模型對原型流動屈服應(yīng)力的預(yù)測精度.選用幾何比例因子1/10,應(yīng)變率數(shù)量級區(qū)間0～2000 s?1.比例模型與原型材料相同,均為Cowper-Symonds 本構(gòu),且D=40 s?1,P=5.對Oshiro 和Alves 的方法(式(2)),根據(jù)文獻[20],給出βV=βq/(q?2)=(1/10)0.077/(0.077?2)=1.097.對Mazzariol 等[21]的方法,采用Cowper-Symonds 本構(gòu)且代入=1,由式(3)計算得到βV=1.067.對本文的最佳逼近直接相似法,根據(jù)式(7)得到βV=1.1904.此外,由于βP=1,根據(jù)1.3 節(jié)分析可知,此時動態(tài)逼近效果最佳,因而不需要考慮調(diào)整比例模型的應(yīng)變率敏感性特征參數(shù).不同方法下,比例模型預(yù)測的無量綱動態(tài)流動屈服應(yīng)力?應(yīng)變率曲線與原型的比較,如圖5 所示.

圖5 不同方法對流動屈服應(yīng)力?應(yīng)變率曲線預(yù)測結(jié)果的比較Fig.5 Comparison of the prediction results for the function curves between the flow yield stress and the strain rate curves by different scaling methods

2 數(shù)值算例驗證

為驗證提出的直接相似方法對結(jié)構(gòu)動態(tài)相似過程的有效性,我們考察一個典型的對應(yīng)變率非常敏感的受質(zhì)量沖擊的折板結(jié)構(gòu)[6,16,20].

2.1 數(shù)值模型

由上下兩端固定在一起的兩塊預(yù)彎曲的方板組成的折板結(jié)構(gòu),頂部受到初始速度V0、質(zhì)量G的剛性質(zhì)量塊沿軸向的沖擊,如圖6 所示.每個半板長為L、寬為B、厚度為H、質(zhì)量為m,兩塊板的初始夾角為2θ0.板的運動分為兩個階段:第一階段,板僅有軸向壓縮,持續(xù)時間較短,如圖6(a)所示;第二階段,軸向壓縮演變?yōu)橐粋€四鉸機構(gòu),其中4 個剛性桿沿著塑性鉸轉(zhuǎn)動,如圖6(b)所示.

圖6 折板結(jié)構(gòu)受軸向質(zhì)量沖擊(a)運動第一階段,(b)運動第二階段Fig.6 Crooked plates under axial impact.(a)First phase of motion,(b)second phase of motion

Tam 和Calladine[44]對第一階段的運動進行了分析,給出結(jié)構(gòu)的運動方程為

其中,γ=(3Np/Lm)1/2,Np=σdA為半板的軸向力,A=BH是板的截面積,w0=Lsin θ0是初始水平位移,σd是使用Cowper–Symonds 本構(gòu)方程得到的流動屈服應(yīng)力.在這個階段,應(yīng)變率被簡化為V0/L,橫向位移為w1=w0cos(γt),當(dāng)轉(zhuǎn)角較小時,sin θ=w/L→θ ≈w/L,因而該階段的轉(zhuǎn)角和角速度分別為

Zhang 和Yu[45]給出了第二階段的運動方程

式中,M1和M2是塑性鉸1 和塑性鉸2 處的彎矩,當(dāng)使用Cowper–Symonds 本構(gòu)方程時,分別為

2.2 結(jié)果分析

對折板結(jié)構(gòu)簡單的量綱分析,輸入?yún)?shù)為:半長L、厚度H、寬度B、初始夾角θ0;沖擊質(zhì)量G、沖擊速度V0; 密度ρ、流動屈服應(yīng)力σd.輸出參數(shù)選為:時間t、轉(zhuǎn)角θ.當(dāng)使用ρ,L,V0為基本量,輸入和輸出參數(shù)的無量綱數(shù)為θ,這與1.1 節(jié)中給出的DLV 無量綱數(shù)是一致的.因而,可使用1.1 節(jié)中的比例關(guān)系對折板結(jié)構(gòu)進行縮放模型試驗.

假定原型結(jié)構(gòu),Lp=0.025 m,Hp=0.001 6 m,Bp=0.051 m,(θ0)p=1.15?,Gp=4.55 kg,(V0)p=7.33 m/s.對比例模型,Lm,Hm,Bm,(θ0)m,Gm,(V0)m分別按照1.1 節(jié)的比例關(guān)系進行縮放; 其中,β 分別取1/4,1/10,1/20,1/100 四種工況,βρ根據(jù)具體材料得到,βV由式(7)計算得到.結(jié)構(gòu)原型的真實應(yīng)變率區(qū)間為()p=0 s?1,()p=(V0)p/2Lp=146.6 s?1,可得真實應(yīng)變率區(qū)間均值為73.3 s?1.為驗證直接相似方法的有效性,粗略的應(yīng)變率區(qū)間取為[0 s?1,200 s?1],其區(qū)間均值為100 s?1,與真實區(qū)間均值量級一致,據(jù)此可使用式(7) 計算速度比例因子βV.為驗證材料應(yīng)變率敏感性效應(yīng)引起的畸變,比例模型和原型均選用典型的應(yīng)變率敏感的軟鋼.為驗證比例模型材料不同于原型引起的畸變,原型選用典型的應(yīng)變率敏感的軟鋼,比例模型選用典型的應(yīng)變率不敏感的鋁合金材料.兩種材料的參數(shù)如表1 所示.根據(jù)1.3 節(jié)的分析,最優(yōu)比例模型材料應(yīng)取參數(shù)P與原型較為接近的材料,顯然比例模型無論選用軟鋼還是鋁合金材料,都是合理的.對不同比例的模型,計算得到的βV如表2 所示.數(shù)值計算得到的轉(zhuǎn)角時間曲線,如圖7 所示.

表1 材料參數(shù)Table 1 Material parameters

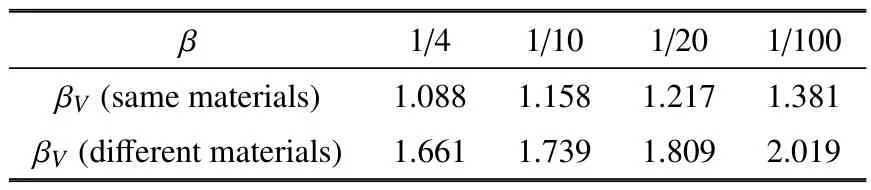
表2 不同比例折板結(jié)構(gòu)模型的速度因子Table 2 The velocity scaling factors for the various geometric crooked plates

圖7 不同比例的折板結(jié)構(gòu)轉(zhuǎn)角?時間曲線Fig.7 Evolution of the rotation with movement time for the various geometric crooked plates

從圖7(a)和圖7(b)可以看出,當(dāng)比例模型使用與原型相同的材料還是不同的材料,折板結(jié)構(gòu)的“時間轉(zhuǎn)角” 響應(yīng)與原型明顯不同; 當(dāng)幾何比例因子從1/4縮放到1/100 時,兩者的“時間?轉(zhuǎn)角” 響應(yīng)差別明顯增大.從圖7(c) 和圖7(d) 可以看出,當(dāng)使用時間、轉(zhuǎn)角的無量綱數(shù)tV0/L、θ 校正有量綱的結(jié)構(gòu)動態(tài)響應(yīng)后,無論比例模型使用與原型相同的應(yīng)變率敏感的軟鋼材料,還是使用與原型不同的應(yīng)變率不敏感的鋁合金材料,都顯示與原型近乎精確的重合.此外,當(dāng)幾何比例從1/4 縮放到1/100 時,這種動態(tài)響應(yīng)的相似關(guān)系仍然是較為精確的.以上分析表明,使用本文提出的直接相似方法進行材料畸變問題的比例模型試驗時,能夠準(zhǔn)確預(yù)測結(jié)構(gòu)原型在沖擊載荷下的動態(tài)響應(yīng).

3 結(jié)論

基于VSG 結(jié)構(gòu)沖擊相似理論,提出了比例模型材料應(yīng)變率敏感性效應(yīng)、屈服應(yīng)力、密度不同于原型引起的畸變問題的一種直接相似方法.與傳統(tǒng)的相似方法相比,該方法不需要預(yù)先測試結(jié)構(gòu)響應(yīng)的信息,適用于不同形式的本構(gòu)方程,重點強調(diào)應(yīng)變率區(qū)間上材料流動屈服應(yīng)力?應(yīng)變率曲線的動態(tài)相似關(guān)系以及材料參數(shù)對這種動態(tài)相似關(guān)系的影響.

首先,針對傳統(tǒng)相似方法存在的缺陷,提出了基于最佳平方逼近的直接相似方法,建立了應(yīng)變率區(qū)間上比例模型預(yù)測的流動屈服應(yīng)力與原型流動屈服應(yīng)力之間的動態(tài)相似關(guān)系,并使用結(jié)構(gòu)原型的應(yīng)變率數(shù)量級的積分區(qū)間替代真實應(yīng)變率積分區(qū)間,直接獲得了修正沖擊速度的速度比例因子或修正密度的密度比例因子.

其次,基于 Norton-Hoff、Cowper-Symonds 和Johnson-Cook 三種經(jīng)典的材料本構(gòu)模型,定性地研究了應(yīng)變率敏感性特征參數(shù)以及參考應(yīng)變率、屈服應(yīng)力、密度的變化對動態(tài)相似性的影響.分析表明,動態(tài)相似關(guān)系最佳逼近效果主要受材料應(yīng)變率敏感性特征參數(shù)的控制,而參考應(yīng)變率、屈服應(yīng)力、密度的影響不大.比例模型選擇應(yīng)變率敏感性特征參數(shù)與原型接近的材料,可獲得最佳動態(tài)逼近效果.在此基礎(chǔ)上,進一步定義了同時調(diào)整材料應(yīng)變率敏感性特征參數(shù)及調(diào)整沖擊速度(或調(diào)整密度)的直接相似方法.

最后,基于Cowper-Symonds 本構(gòu)模型,比較了本文提出的最佳逼近直接相似方法和傳統(tǒng)直接相似方法的預(yù)測精度,并使用受集中質(zhì)量沖擊的折板結(jié)構(gòu),進一步驗證了本文提出的直接相似方法的優(yōu)勢.結(jié)果表明,傳統(tǒng)的直接相似方法對流動屈服應(yīng)力預(yù)測誤差較大,而本文提出的直接相似方法預(yù)測精度較高.對于應(yīng)變率敏感性效應(yīng)、屈服應(yīng)力、密度不同引起的畸變問題,本文提出的直接相似方法,即便對1/100 的折板結(jié)構(gòu)比例模型,仍能夠準(zhǔn)確預(yù)測原型的動態(tài)響應(yīng).