Hilbert空間中逼近對偶框架的構造

倪德果，江 震，楊守志

（汕頭大學理學院，廣東 汕頭 515063）

0 引言

1952年，Duffin和Schaeffer[1]在研究非調和分析問題時，提出了框架的概念.但直到1986年，Daubechies等人的工作才使得人們開始真正地關注到框架理論.框架作為基的推廣，由于它的冗余性，使得框架的設計更加地靈活，從而比基能夠更好地解決信號處理和傳輸過程中產生的一些問題，因而框架理論在信號處理，無線通信等領域得到了較為廣泛的應用和發展.

經過學者們多年的努力，框架理論取得了豐碩的成果，如：Daubechies和Bin[2]研究了小波框架的典范對偶框架，Gr?chenig[3]提出了Banach空間上對偶框架的概念.但借助框架的典范對偶框架去重構信號要涉及到求框架算子的逆算子，通常求逆算子的運算量很大或者無法進行.對于借助于框架的對偶框架重構信號，計算框架的對偶框架也是較為復雜的[4].學者們開始尋求方法去逼近對偶框架，見文獻[5-6]，Christensen等[7]人提出了逼近對偶框架的概念和一些構造方法.近年來很多學者也對逼近對偶框架的構造和性質進行了研究，如：Khosravi[8]研究了g-框架的逼近對偶框架，Javanshiri[9]研究了Hilbert空間上逼近對偶框架的一些性質，張偉[10]研究了逼近對偶Hilbert-Schmidt框架等.

本文在第一部分回顧了框架理論的一些基礎知識.在第二部分得到了構成逼近對偶框架的一些充分條件和構造方法，首先研究了利用框架的倍數去構造逼近對偶框架.如果是框架，的對偶框架或逼近對偶框架，通過適當的選擇實數a，b，之間可構成逼近對偶框架，之間也可構成逼近對偶框架.當U，V是有界線性算子時，之間可構成逼近對偶框架，之間也可構成一對逼近對偶框架.然后研究了通過兩個框架的線性組合構造逼近對偶框架，包括框架的兩個對偶框架的線性組合，框架和它的對偶框架的線性組合，框架的對偶框架和框架的逼近對偶框架的線性組合，框架的兩個逼近對偶框架的線性組合及框架的對偶框架擾動后得到的兩個序列的線性組合和原框架之間都可構成一對逼近對偶框架.在第三部分，構造了一些例子.文章中Hilbert空間簡記為H，H到H上全體有界線性算子組成的集合簡記為B（H）.

1 預備知識

首先回顧一下Hilbert空間中有關框架的基礎知識.

定義1.1設是Hilbert空間H上的序列，如果存在常數A，B＞0，對于任意的f∈H，使得

如果{fk}∞k＝1是 Bessel序列，定義 T 是的合成算子，有T算子是線性的，有界的，且.定義 T*是的分析算子，定義S是框架算子，有如果是 Bessel序列，定義U是的合成算子，定義U*是的分析算子，定義V是復合框架算子，有

定義1.2設是Hilbert空間H上的Bessel序列，如果對于任意的f∈H，使得

其中，

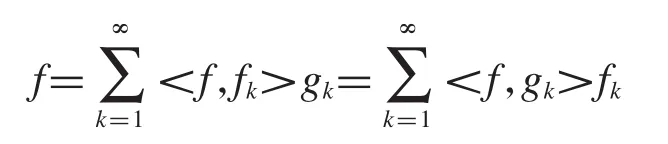
稱上式為完美重構.

定義1.3設是Hilbert空間H上的Bessel序列，如果存在0≤ε＜1，對于任意的f∈H，使得

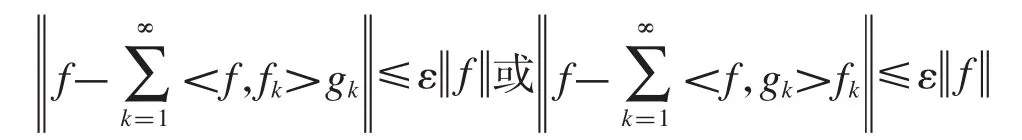
2 逼近對偶框架的充分條件

2.1 利用框架乘以系數構造

在文獻[11]中，Azandarani給出了這樣的一個論述，設是Hilbert空間中的標準正交基，如果任意實數0＜a＜2，則的逼近對偶框架.當是框架時，a需要滿足什么條件，可以構成一對逼近對偶框架.

定理2.1[12]設是Hilbert空間H上的框架，上、下框架界分別為B、A，且A、B＞0，框架算子記為S，如果任意實數那么的逼近對偶框架.

由 Gr?chenig[13]91，（1-aB）I≤I-aS≤（1-aA）I.

由于

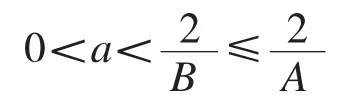
所以

通常顯式構造對偶框架的方法[14]159較為復雜，而在定理2.1中，僅通過框架乘以一個系數就構造出了一對逼近對偶框架.我們可以通過調整a，趨于完美重構.當為標準正交基時，我們會發現Azandarani在文獻[11]中的論述是該定理的一個推論.我們可以看到Christensen在文獻[7]和Javanshiri在文獻[9]中的論述也是該定理的推論.

推論2.2設是 Hilbert空間的框架，B、A 是的上、下框架界，則是的逼近對偶框架.

推論2.3設是Hilbert空間中的框架，上框架界為M，則的逼近對偶框架.

定理2.4設任意非零實數0＜ab＜2，設是Hilbert空間中的框架，上、下框架界分別為B，A，的對偶框架，則是一對逼近對偶框架.

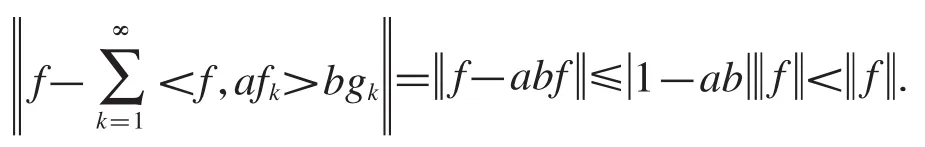
由于對偶框架是逼近對偶框架的特殊情況，于是當ab＝1時，得到構成一對對偶框架.

推論2.5在定理2.4的條件下，當ab＝1時，是一對對偶框架.

定理2.6設任意非零實數a，b，且ab＝1，是 Hilbert空間中的框架，的逼近對偶框架，則是一對逼近對偶框架.

定理2.7設是Hilbert空間中的框架，的對偶框架，U、V∈B（H），且，則是一對逼近對偶框架.

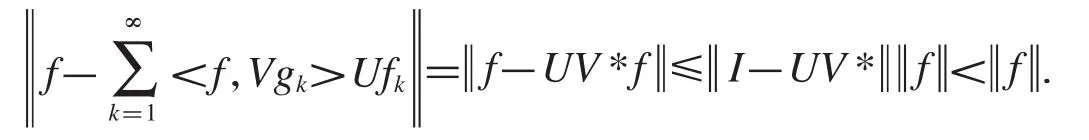
推論2.8設是Hilbert空間中的標準正交基，U、V是B（H）中的可逆算子，當，則是Riesz基，并且構成一對逼近對偶框架.

推論2.9設是Hilbert空間中的標準正交基，U、V是B（H）中的滿射算子，當，則是框架，并且構成一對逼近對偶框架.

我們通過Hilbert空間中的標準正交基和有界線性算子，構造出了一對逼近對偶Riesz基和逼近對偶框架.

定理2.10設是 Hilbert空間中的框架，的逼近對偶框架，V 是和的復合框架算子，U是B（H）中的一個酉算子，且U*和V可交換，則和是一對逼近對偶框架.

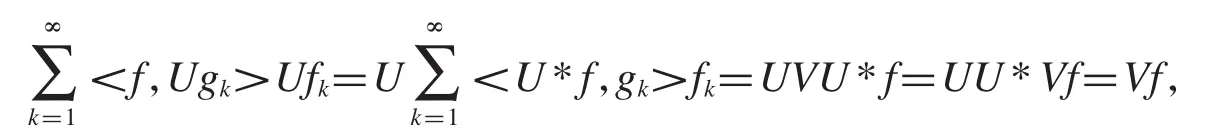
定理2.11設是 Hilbert空間中的一對逼近對偶框架，U、V∈B（H），a，b是非零實（復）數，當U＝aI，V＝bI時，是一對逼近對偶框架等價于和是一對逼近對偶框架.

2.2 利用兩個框架的線性組合構造

這一部分我們將研究通過兩個框架的線性組合構造逼近對偶框架，首先研究地是通過兩個對偶框架的線性組合去構造逼近對偶框架.

定理2.12設任意非零實數是 Hilbert空間中的框架，的兩組對偶框架，hk＝agk＋bg'（kk＝1，2，3，…），如果0＜a＋b＜2，則是一對逼近對偶框架.

證明 由題意得，

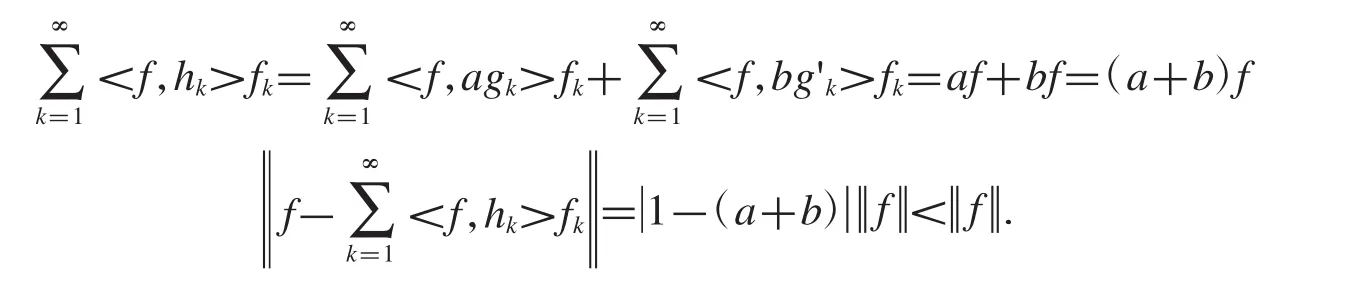
由于對偶框架是逼近對偶框架的特殊情況，所以當a＋b＝1時，我們得到框架和它的兩組對偶框架的線性組合之間構成是一對對偶框架.

推論2.13在定理2.12的條件下，如果a＋b＝1，則是一對對偶框架.

定理2.14設是Hilbert空間中的框架，框架算子記為S，的對偶框架，hk＝fk＋g（kk＝1，2，3，…），且滿足S＜1，則是一對逼近對偶框架.證明 已知是 Hilbert空間中的框架，易知是 Hilbert空間中的 Bessel序列.

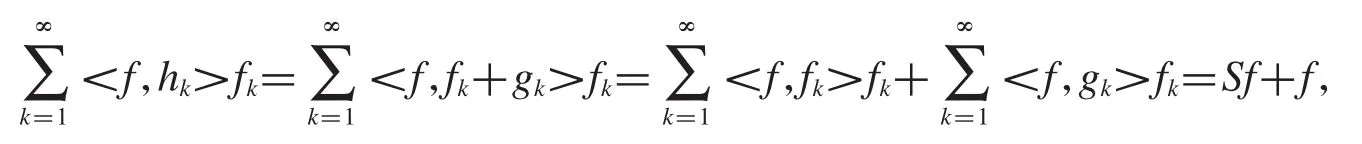
定理2.15設是 Hilbert空間中的框架，的對偶框架，的逼近對偶框架，hk＝gk＋g'（kk＝1，2，3，…），則是一對逼近對偶框架.

定理2.15的證明過程與定理2.14類似，這里不再贅述.在逼近對偶框架的定義中，我們把ε不妨看成趨于完美重構的誤差上限，這樣得到了下面兩個定理.

定理2.16設是 Hilbert空間的框架，的兩個逼近對偶框架，ε0記為關于的趨于完美重構的誤差上限，ε1記為關于的趨于完美重構的誤差上限，且滿足 ε0＋ε1＜2，則是一對逼近對偶框架.

證明

定理2.17設a，b是非零實（復）數，是 Hilbert空間的框架，的兩個逼近對偶框架，V1記為的復合框架算子，V2記為的復合框架算子，ε0記為關于的趨于完美重構的誤差上限，ε1記為關于的趨于完美重構的誤差上限，且滿足，則是一對逼近對偶框架.

證明

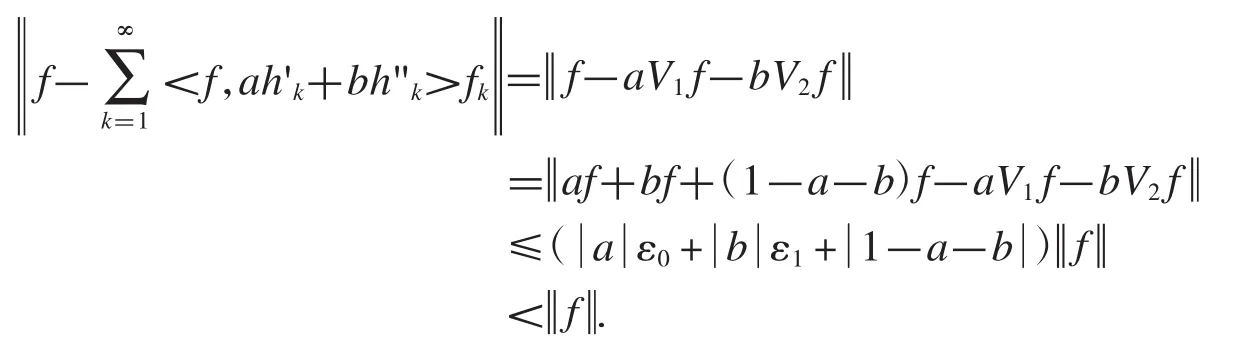
定理2.18設是Hilbert空間的框架，上、下框架界為A，B，的對偶框架，上框架界為是Hilbert空間中的序列，如果存在常數對于任意的有限序列{ck}，使得

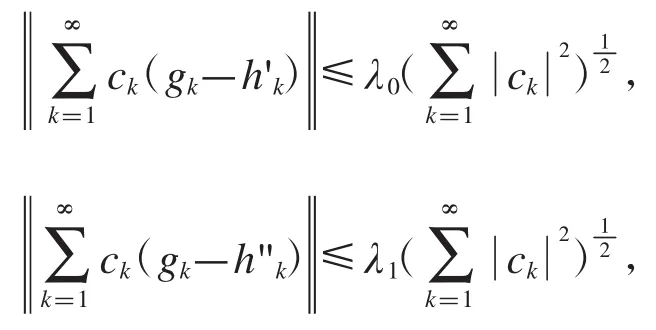
成立，對于任意的f∈H，則有

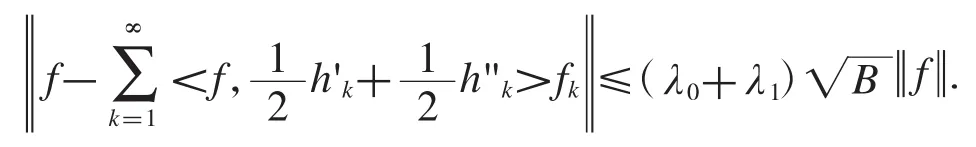
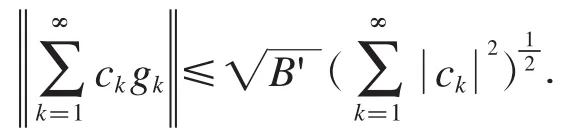
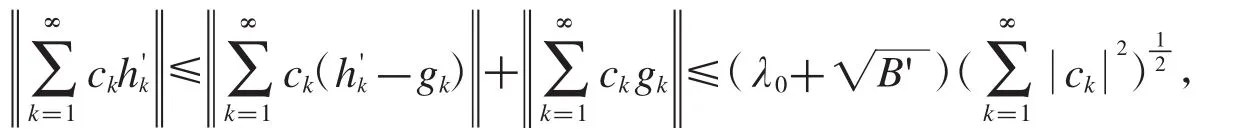
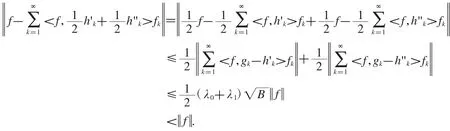
3 例子

這一部分，我們給出了關于前面的部分定理的一些例子，并且我們發現可以通過調整a，b的取值，去趨于完美重構.

考慮H＝C2，標準正交基為{e1，e2}，令

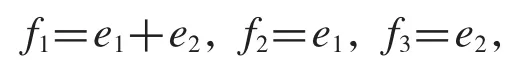
例3.1構造關于定理2.1的例子，取，計算驗證得，的逼近對偶框架，且求得的ε不同，這也表明我們可以通過選擇適當的a趨于完美重構.

例3.2構造關于定理2.4和推理2.5的例子，通過計算得，其典范對偶框架為

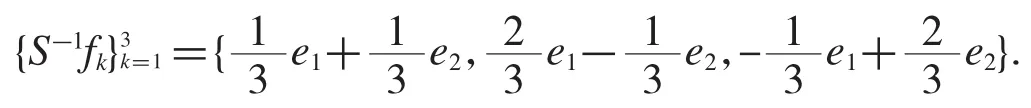
例3.3構造關于定理2.12和推論2.13的例子，通過文獻[14]159的方法，我們構造出了的一個對偶框架為取另一個對偶為當取驗證得構成一對逼近對偶框架.當取，驗證得構成一對對偶框架.