關于Neuman-Sándor平均的一個較強上下界估計
2020-06-12 01:54:26吳善和
汕頭大學學報(自然科學版) 2020年2期
關鍵詞:研究
何 燈,吳善和
(1.福清第三中學,福建 福清 350315;2.龍巖學院數學與計算機科學學院,福建 龍巖 364012)
0 引言
二元平均之間的比較,一直是不等式研究的一個熱點.2003年及2006年,Neuman E與Sándor J在文獻[1-2]中定義Schwab-Borchardt平均SB(a,b),該平均可衍生出許多常見的平均,如第一類 Seiffert平均 P(a,b),第二類 Seiffert平均 T(a,b),Neuman-Sándor平均 M(a,b),對數平均 L(a,b).近幾年,Neuman-Sándor平均和其他二元平均得到深入的研究.特別地,從有關Neuman-Sándor平均與其他二元平均或它們的各類組合比較中發現了許多重要的結論,參見文獻[1-16].
在現有研究的基礎上,筆者對Neuman-Sándor平均M(a,b)的相關結果進行匯總比較,發現算術平均 A(a,b)與第二類 Seiffert平均 T(a,b)能夠更精確構造出 M(a,b)的上下界.在此基礎上,構造M(a,b)的一類上下界模型,建立M(a,b)的一個較強上下界估計.
1 預備知識
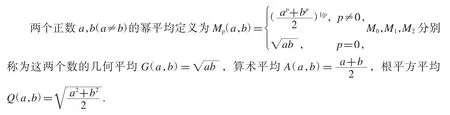
2 引理及證明


3 主要結論及證明


定理得證.
注可見式(4)的強度.
下面提出一個猜想,供有興趣的讀者探究.
猜想雙邊不等式
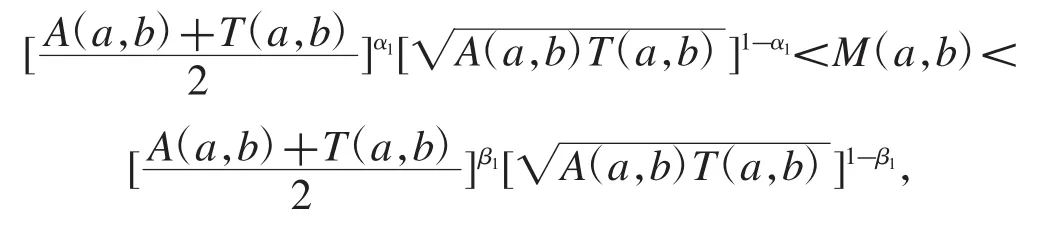
猜你喜歡
體育科技文獻通報(2022年3期)2022-05-23 13:46:54
天津外國語大學學報(2021年3期)2021-08-13 08:32:18
遼金歷史與考古(2021年0期)2021-07-29 01:06:54
科技傳播(2019年22期)2020-01-14 03:06:54
遼金歷史與考古(2019年0期)2020-01-06 07:45:20
民用飛機設計與研究(2019年4期)2019-05-21 07:21:24
電子制作(2018年11期)2018-08-04 03:26:04
汽車工程學報(2017年2期)2017-07-05 08:13:02
國際商務財會(2017年8期)2017-06-21 06:14:14
電子制作(2017年23期)2017-02-02 07:17:19

