一種錨泊條件下捷聯慣導系統級標定方法

楊小康，嚴恭敏，李四海

（西北工業大學自動化學院，西安 710129）

慣性測量組合（IMU,Inertial Measurement Unit）是慣性導航系統的核心，IMU標定的目的是確定其數學模型或誤差數學模型的參數[1]，標定結果直接影響導航精度[2]。目前常見的是捷聯慣性測量組合（SIMU），SIMU通常由三個陀螺和三個加速度計組成，陀螺和加速度計輸出中存在零偏誤差、刻度系數誤差、安裝誤差和隨機噪聲[3]。標定分為分立式標定和系統級標定，前者根據各個陀螺和加速度計輸出與參考輸入間的關系進行標定，后者則是基于導航解算誤差原理，利用導航誤差估計慣性器件誤差[2]。相比于分立式標定，系統級標定可以實現外場標定和慣導系統自標定，標定精度不依賴轉臺精度，不需要記錄陀螺和加速度計輸出數據[4]。無論是高精度SIMU還是消費級SIMU都可以通過多位置轉動實現基本誤差參數標定[5]。SIMU標定大多在實驗室環境進行，標定時拆卸和搬運設備給SIMU維護帶來不便[6]，因此需要研究非實驗室環境下外場標定和自標定技術。

外場環境的干擾運動使標定量測不準確，影響SIMU標定結果，所以外場試驗需要對標定方法進行改進。對于低精度SIMU可以通過檢測轉動過程中的靜止狀態，在手動轉動條件下完成標定，試驗表明此方法可以估計出陀螺和加速度計刻度系數誤差及安裝誤差[7]。外場標定研究大多在陸上或者艦船系泊狀態下進行[8,9]，艦船錨泊條件下的研究尚未見相關文獻，但研究艦船錨泊條件下SIMU外場標定方法有很大的應用價值。首先，大型艦艇的自持力不斷提升一般可以達到60天甚至更長，一次出海周期可達1年，期間沒有條件對SIMU進行實驗室環境標定。其次，艦船上武器裝備種類多、數量大，對使用中低精度SIMU的戰術武器，簡單標定后補償SIMU器件誤差能顯著提升其導航精度。

在地面環境進行外場標定時可保持SIMU靜止，轉位機構使SIMU轉過不同角位置，利用濾波方法估計出SIMU器件誤差。但是艦船在水面上會受到風浪等各種因素影響，即使在錨泊狀態也不是靜止不動的。受到風和海浪的影響，艦船會產生沿著船體坐標系三個軸的線運動和角運動[10]。錨泊狀態，船體在錨鏈力作用下還會出現偏蕩運動。偏蕩運動是錨泊船在風、流、浪和錨鏈力的約束作用下，圍繞錨泊作用點產生的周期性低頻振蕩狀態[11]。因為錨泊條件下艦船會受到錨鏈力和風、浪、流等作用力的綜合影響，所以與系泊條件相比錨泊運動速度更大且規律性較差。進行錨泊條件系統級標定時無法消除錨泊運動的影響，因此錨泊條件下進行系統級標定難度更大。

本文針對在艦船錨泊和無其他導航系統輔助條件下進行SIMU系統級標定的問題，首先建立艦船錨泊條件下運動簡化模型，分析錨泊運動特點，得到標定時干擾運動的規律。然后根據慣導誤差方程建立捷聯慣導誤差狀態空間模型，設計卡爾曼濾波器，再根據錨泊運動干擾速度設置合適的濾波參數使SIMU誤差參數估計結果收斂、穩定。最后進行仿真，并比較靜基座和錨泊條件系統級標定結果，檢驗錨泊條件系統級標定的效果。

1 海上錨泊運動模型

艦船在水面運動時，產生的橫蕩、縱蕩、升沉、艏搖、橫搖和縱搖都是周期性運動，周期一般在1～30 s之間[10]。船體產生偏蕩運動時，重心將描繪一個與風向橫交的“∞”形軌跡。偏蕩運動的橫移幅度和船艏轉動角度都會隨著風速和鏈長增加而增加。圖1是一種真實的偏蕩運動軌跡[11]，圖中O為偏蕩中心，Ox軸為橫蕩方向，Oy軸為縱蕩方向。為了方便分析，對偏蕩運動模型進行簡化，以橫縱方向兩個垂直的周期運動來描述偏蕩運動。

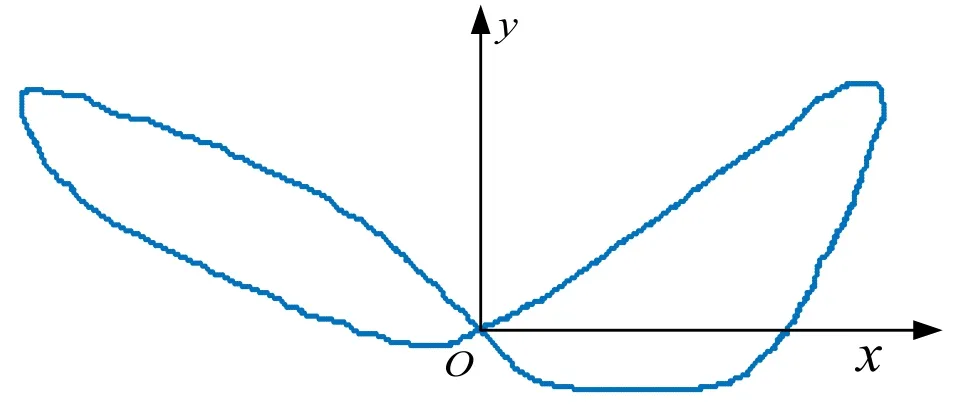
圖1 一種偏蕩運動軌跡Fig.1 A trajectory of the anchoring motion

偏蕩運動模型包含橫向、縱向位移以及運動周期三個參數，分別用sx、sy和T表示。簡化后偏蕩運動數學模型為

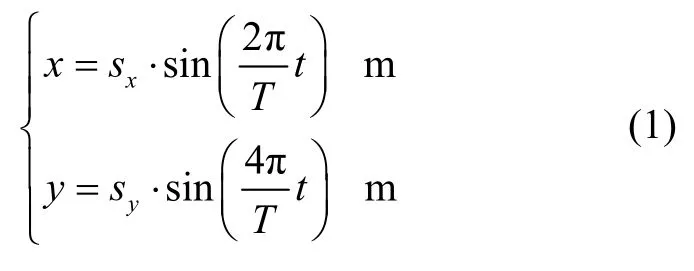
式中，x表示橫蕩方向位置坐標，y表示縱蕩方向位置坐標。偏蕩距離sx與平均偏蕩速度關系為

偏蕩運動橫向平均速度的估算公式為

式中，vas表示風速，Ba/Ld表示艦船水線上下側面積比，P/Lpp表示風作用中心到船中心距離與兩柱間長之比，Lc/H表示鏈長與水深之比。根據上述參數計算出偏蕩運動平均速度，再由式（2）計算橫向運動幅度。艦船縱向偏蕩運動幅度小于橫向幅度，一般為橫向幅度的0.2～0.6倍，即

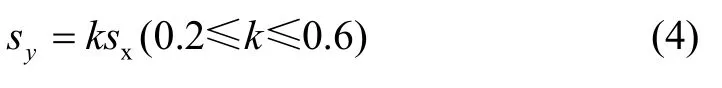
根據式(1)～(4)可以估算出偏蕩運動速度和位置。

在后文錨泊條件系統級標定仿真中，假設偏蕩運動的橫蕩幅度為75 m，縱蕩幅度為30 m，偏蕩運動周期為600 s。偏蕩運動簡化模型軌跡如圖2所示。

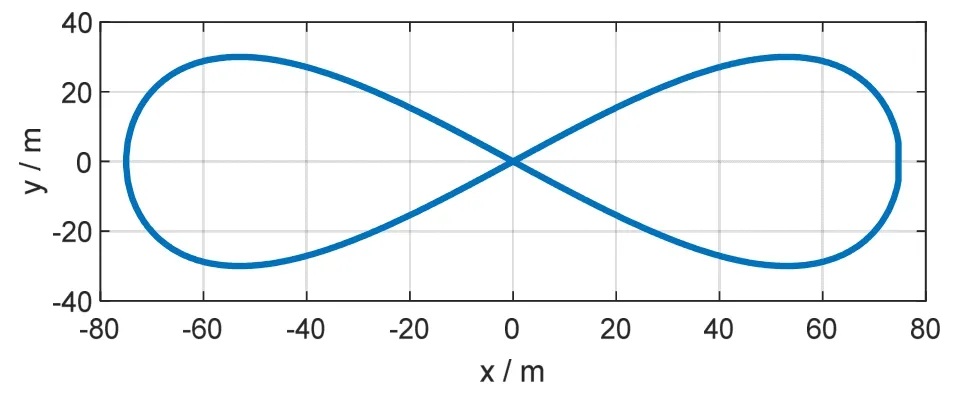
圖2 簡化后偏蕩運動軌跡Fig.2 Simplified trajectory of the anchoring motion

2 SIMU靜基座系統級標定方法

系統級標定常用卡爾曼濾波，將SIMU誤差參數作為狀態量。陀螺輸出角速度誤差和加速度計輸出比力誤差為

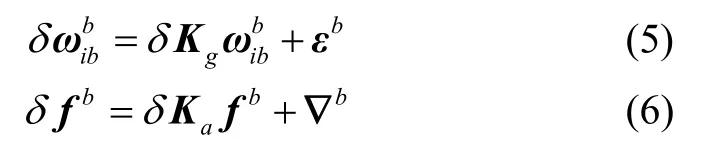
式中，δKg和δKa分別是陀螺和加速度計刻度系數誤差矩陣，εb和 ?b分別是陀螺和加速度計常值零偏。δKg和δKa均是3階方陣，由于存在安裝誤差角約束，只需要估計兩個矩陣中的9個安裝誤差。所以在誤差模型中設定

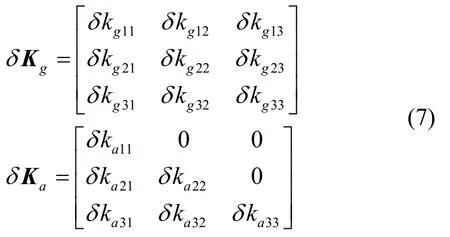
后文用δkgii和δkaii表示刻度系數誤差，δkgij和δkaij（i≠j）表示安裝誤差。

根據捷聯慣導誤差方程，選取卡爾曼濾波狀態空間模型30維狀態向量為

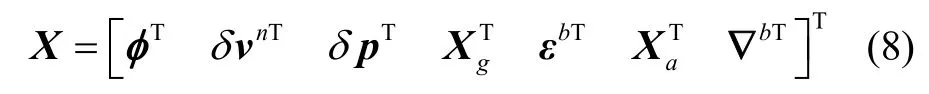
式中，φ=［φEφNφU］T為姿態失準角，δvn為導航系下速度誤差，δp=［δLδλ δh］T為導航位置誤差（三個分量依次為緯度誤差、經度誤差和高度誤差），Xg和Xa分別為陀螺和加速度計刻度系數誤差矩陣中元素組成的列向量

根據捷聯慣導誤差方程和式(8)給出的狀態向量，構建濾波器系統方程

式中，F為狀態轉移矩陣，G為系統噪聲分配矩陣，W為陀螺和加速度計輸出中的白噪聲向量。F中各個元素根據捷聯慣導誤差方程確定。

靜基座系統級標定時SIMU速度為零且位置不變，所以可以選擇零速度和初始位置作為導航結果基準，以此構建量測方程

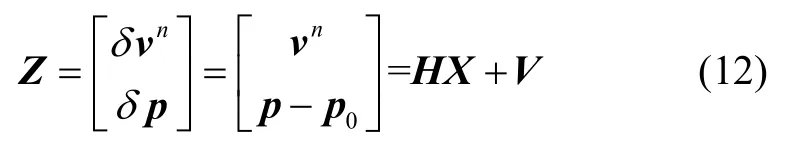
式中，vn表示慣導輸出導航系速度，p=［Lλh］T為慣導輸出位置向量（緯度、經度和高度），p0表示初始位置，觀測矩陣H=［06×3I6×606×21］，V為量測噪聲。

標定過程中還需要通過狀態可觀測性分析，確定合適的轉臺轉動方案，使狀態向量中SIMU誤差參數全部可觀。表1列出了一組包含15次轉動的轉動編排方案[12]，初始時刻SIMU坐標系“X-Y-Z”軸指向“東-北-天”。靜基座系統級標定實驗中每個位置通常靜止60s，動基座標定實驗中可根據標定條件增加每個位置靜止時間。

表1 系統級標定轉動編排Tab.1 Rotation plan of system-level calibration

按照圖3所示在三軸轉臺上安裝SIMU，依表1給出的轉臺轉動方案進行一組15位置轉動，每次轉動后靜止一段時間。利用標定過程的SIMU輸出完成卡爾曼濾波就可以估計出SIMU誤差參數。

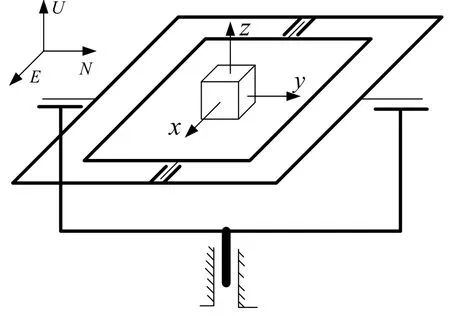
圖3 系統級標定SIMU安裝示意圖Fig.3 SIMU install sketch of system-level calibration

3 艦船錨泊條件系統級標定

系統級標定中，根據式(11)和式(12)可得離散化狀態空間模型

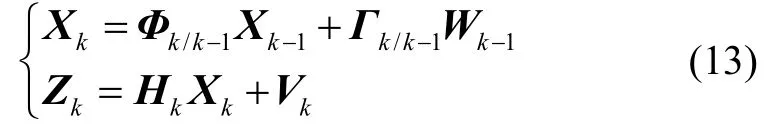
式中，Φk/k-1為狀態一步轉移矩陣，Γk/k-1為系統噪聲分配矩陣，Hk為觀測矩陣；Wk為系統噪聲，Vk為量測噪聲，兩者互不相關，且。因為靜基座下量測準確，Rk設置較小的值即可，而動基座標定算法中，需要根據運動特點選取合適的量測噪聲參數。

在錨泊條件下，艦船速度和位置不斷變化，在無其他導航系統輔助的條件下無法得到準確的慣導誤差。如果用慣導速度和位置作為濾波量測，則錨泊運動的速度和位置都會影響SIMU誤差參數的估計精度，所以錨泊條件系統級標定只用速度誤差作為量測，在算法設計時只需考慮錨泊運動速度干擾的影響，便于濾波器量測噪聲參數設置。在錨泊條件下，SIMU輸出速度為

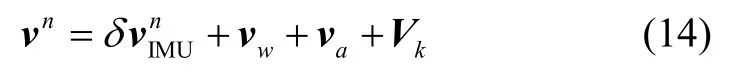
式中，vn為慣導系統輸出速度，為SIMU器件誤差激勵出的速度誤差，vw為艦船短周期振蕩速度，va為艦船錨泊偏蕩運動速度，Vk為量測噪聲。記，則量測向量為

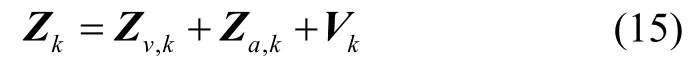
在卡爾曼濾波更新中，濾波增益更新為

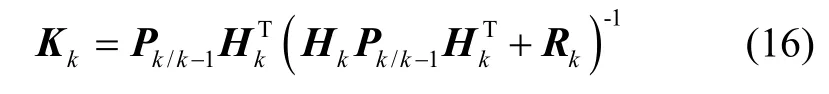
狀態更新公式為

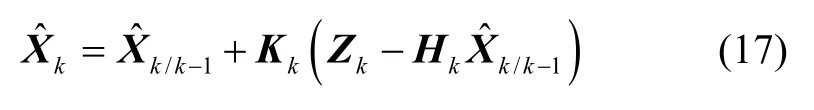
根據式(15)和式(17)，錨泊條件系統級標定的狀態更新公式為

式中，由錨泊運動引起的KkZa,k會影響系統級標定狀態更新結果。

按照靜基座系統級標定參數設置經驗，量測噪聲方差陣一般取值較小，按式(16)和式(18)計算卡爾曼濾波過程狀態更新時，速度誤差量測向量中錨泊運動產生的干擾會影響SIMU誤差參數估計。以陀螺和加速度計安裝誤差角為例，當速度量測誤差設置為0.01m/s時進行不同條件的4組錨泊條件系統級標定，補償后的兩個誤差角δkg31和δka31如圖4和圖5所示。由于量測誤差小，濾波時錨泊運動干擾速度會被錯誤地引入慣導系統誤差估計中，使得誤差參數估計結果隨錨泊運動波動，影響誤差參數估計。

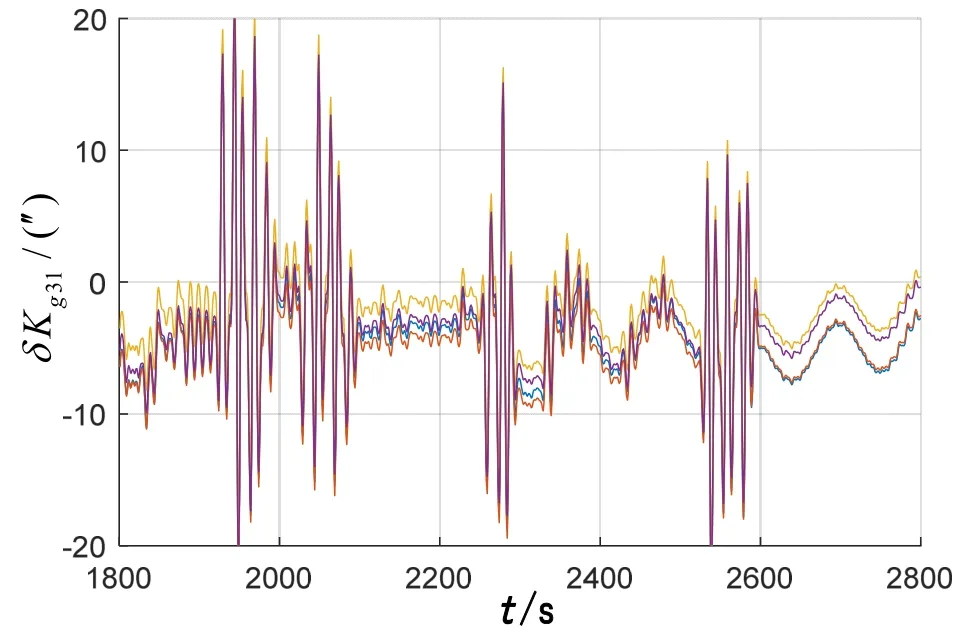
圖4 系統級標定過程 δkg31的變化Fig.4 Plot of δkg31in system-level calibration process

圖5 系統級標定過程 δka31的變化Fig.5 Plot of δka31in system-level calibration process

根據以上分析，錨泊條件系統級標定時應當按照錨泊運動速度大小設置Rk，以減小干擾速度的影響。可以設置速度量測噪聲方差為最大錨泊運動速度k倍的平方，即

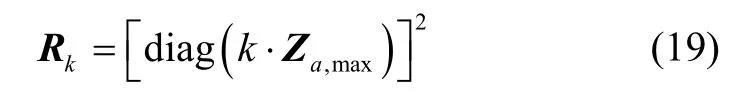
式中，diag（v）表示向量v作為對角元素構成的對角陣，Za,max表示錨泊運動最大速度，參數k可取不同值進行錨泊條件系統級標定仿真，根據仿真結果確定合適的數值。假設艦船錨泊狀態下兩個水平速度波動幅度均為0.6 m/s，垂向速度波動幅度為0.2 m/s。設置不同的慣導誤差參數，取k為0.001、0.01、0.1和1分別進行20次系統級標定蒙特卡洛仿真，得到SIMU各類誤差項標定補償后殘差的最大值，如表2所列。

表2 不同量測噪聲方差下的系統級標定結果Tab.2 Calibration result with different variance of measurement noise

表2中所示的各標定誤差為同類誤差的最大值。根據表2中的仿真結果，錨泊條件系統級標定時應取k= 0.1，按0.1倍最大錨泊速度設置速度量測噪聲方差陣得到的標定結果比較準確，且濾波器狀態估計值不隨干擾運動波動。為了在SIMU標定時得到更準確的標定結果，還可以在0.1附近繼續取值進行仿真，尋找更優的量測噪聲參數。

進行艦船錨泊條件系統級標定實驗時，可根據海上風、浪和艦船特征等參數估算出錨泊運動幅度和周期，然后建立海上錨泊運動模型并進行仿真分析，確定出合適的量測噪聲方差參數，以得到錨泊干擾下最準確的SIMU誤差參數標定結果。

4 系統級標定仿真

仿真中設置4組不同的SIMU誤差參數，每組仿真5次，誤差參數如表3所列。以每一類誤差標定補償后殘差的最大值來進行標定結果比較。

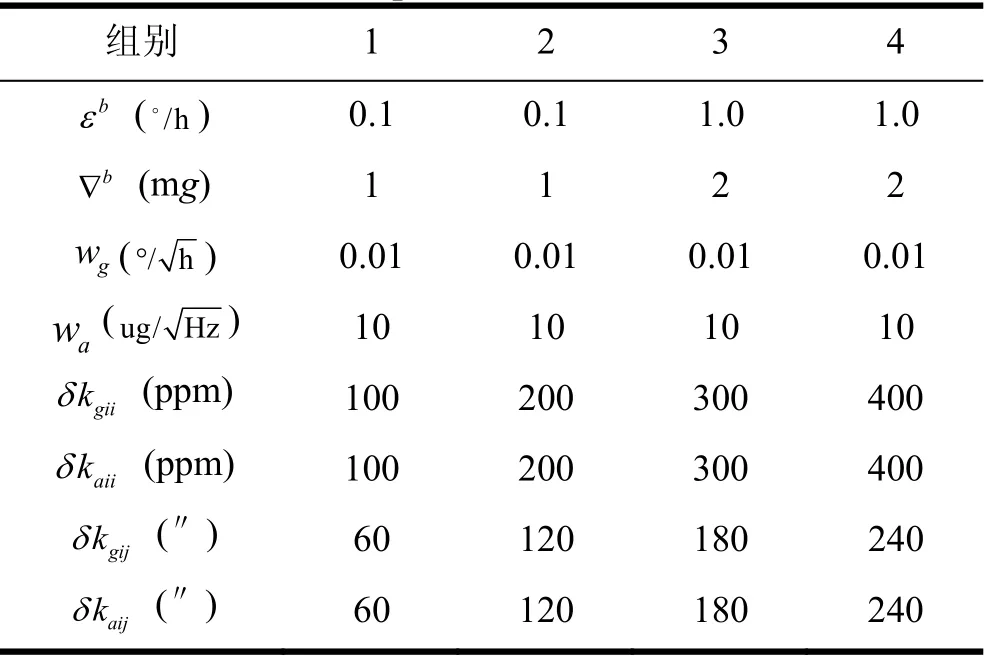
表3 SIMU誤差參數表Tab.3 Error parameter table of SIMU

為了方便比較，分別進行靜基座條件和錨泊條件兩組系統級標定仿真。靜基座系統級標定根據表1的方案進行轉動，標定時間為1400 s，標定結果如表4所列，經過標定補償后捷聯慣導誤差中陀螺零偏數值較大，其余誤差顯著降低。

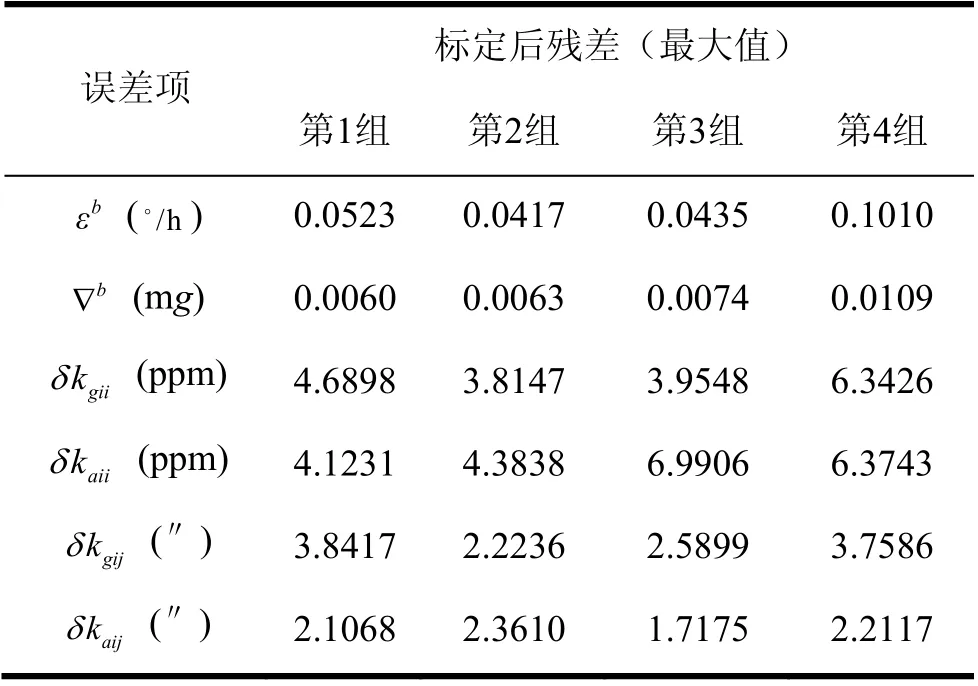
表4 靜基座系統級標定誤差Tab.4 Result of system-level calibration on stationary base

錨泊條件動基座系統級標定仿真時按照第1節中的簡化偏蕩運動模型進行艦船偏蕩運動仿真。同時加入幅值為7°的橫搖運動，15°的縱搖運動，0.25m的橫蕩和縱蕩，以及0.5m的升沉運動，以上運動的周期為10s。由于錨泊條件系統級標定中量測噪聲方差較大，量測中存在錨泊運動干擾，因此與靜基座條件相比量測向量中有效信息較少。延長標定時間可增加量測信息，且慣導誤差增大可以提升量測中慣導誤差占比，所以錨泊條件仿真時延長標定時間至2800s。20組錨泊條件仿真中慣導誤差標定后殘差變化如圖6～12所示，圖中左側為標定全程的估計殘差變化，右側為最后800 s的變化曲線，標定結果見表5。

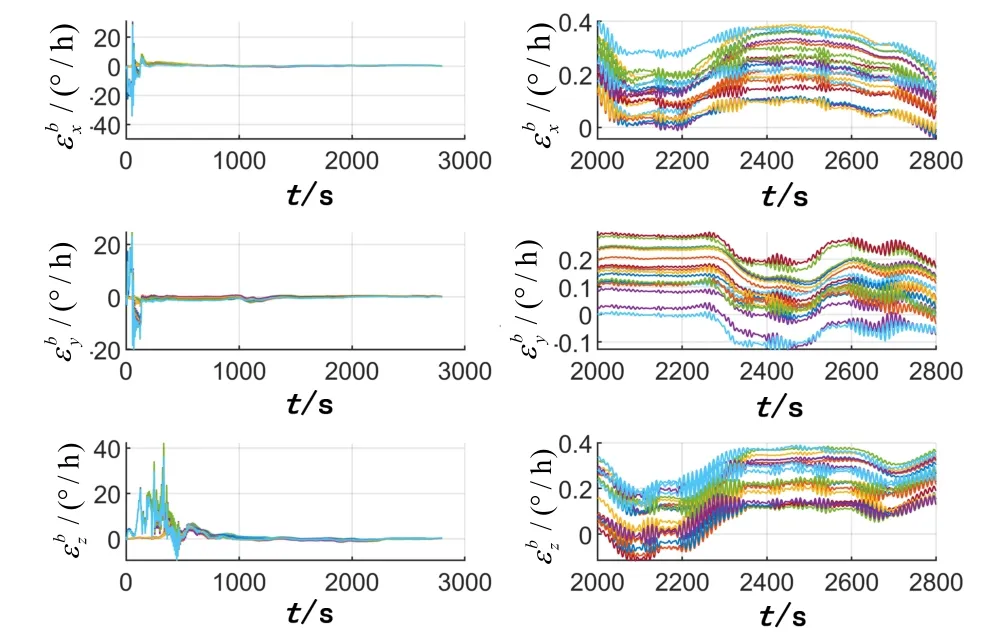
圖6 系統級標定陀螺零偏誤差Fig.6 Calibration result of gyroscope bias error

圖7 系統級標定加速度計零偏誤差Fig.7 Calibration result of accelerometer bias error

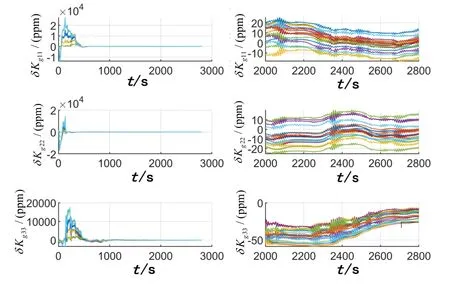
圖8 系統級標定陀螺刻度系數誤差Fig.8 Calibration result of gyroscope scale factor error

圖9 系統級標定加速度計刻度系數誤差Fig.9 Calibration result of accelerometer scale factor error

圖10 系統級標定陀螺安裝誤差Fig.10 Calibration result of gyroscope misalignment error

圖11 系統級標定陀螺安裝誤差Fig.11 Calibration result of gyroscope misalignment error

圖12 系統級標定加速度計安裝誤差Fig.12 Calibration result of accelerometer misalignment error

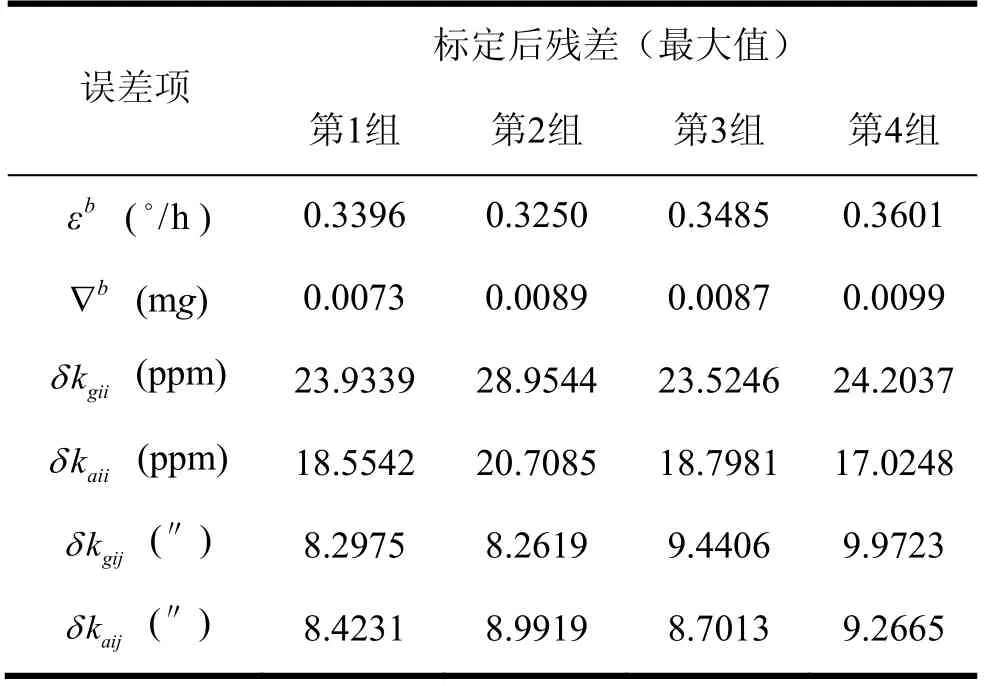
表5 錨泊條件系統級標定仿真結果Tab.5 Result of the system-level calibration under anchoring condition

從圖6～12可以看出，在不同仿真條件下SIMU誤差參數估計結果都是收斂的，雖然最后階段受錨泊運動影響部分結果依然有波動，但是都穩定在小量范圍內。根據表5中錨泊條件系統級標定結果可以得出結論：陀螺零偏標定結果較差，難以通過動基座系統級標定補償SIMU陀螺零偏；加速度計零偏標定結果較準確，標定誤差小于 1× 10-5g；刻度系數誤差標定結果一般，陀螺刻度系數誤差標定誤差小于29.0 ppm，加速度計小于20.8 ppm；SIMU安裝誤差角標定比較準確，陀螺和加速度計安裝誤差角的標定誤差分別小于10.0''和9.3''。

5 結 論

SIMU外場標定技術應用廣泛，可以利用卡爾曼濾波估計SIMU誤差參數，但外場標定大多都是在地面環境或艦船系泊狀態下進行，現有標定方法尚不能進行艦船錨泊條件下SIMU外場標定。

本文分析艦船錨泊條件運動特點，提出一種錨泊條件下SIMU系統級標定方法。此方法可以在艦船錨泊條件下完成SIMU誤差參數標定，補償SIMU的加速度計零偏、陀螺和加速度計刻度系數誤差以及陀螺和加速度計安裝誤差角。仿真結果表明，錨泊條件下系統級標定方法可以補償SIMU中大部分誤差，提升導航精度。錨泊條件系統級標定方法可以在艦船長時間出海期間，不依賴其他導航系統實現艦上SIMU系統級標定，提升SIMU導航精度，有一定的應用參考價值。