一種改進(jìn)的姿態(tài)匹配船體變形測(cè)量方法

張 濤,王 帥，劉興華

（1.東南大學(xué)儀器科學(xué)與工程學(xué)院,南京 210096;2.微慣性?xún)x表與先進(jìn)導(dǎo)航技術(shù)教育部重點(diǎn)實(shí)驗(yàn)室,南京 210096）

現(xiàn)代艦船都裝備有各種高精度導(dǎo)航設(shè)備，為了能使這些設(shè)備正常協(xié)調(diào)工作，必須有一個(gè)統(tǒng)一的空間坐標(biāo)基準(zhǔn)系統(tǒng)。但是，由于艦船并不是一個(gè)絕對(duì)剛體以及船體自身重量和溫度、海浪沖擊等外部環(huán)境的影響，使得船體和甲板產(chǎn)生微小變形。根據(jù)俄羅斯學(xué)者A.V.Mochalov所述，艦船甲板變形角最高可達(dá)1°～1.5°，動(dòng)態(tài)撓曲變形也可達(dá)角分量級(jí)[1]。由于船體變形的影響，使艦船設(shè)備獲得的姿態(tài)信息不再準(zhǔn)確，而船載設(shè)備一般都是高精度設(shè)備，微小的變形也會(huì)使設(shè)備性能受到嚴(yán)重影響。因此，對(duì)船體變形角進(jìn)行實(shí)時(shí)測(cè)量和補(bǔ)償，以保證船載設(shè)備在統(tǒng)一的基準(zhǔn)坐標(biāo)系下完成高精度工作成為近年來(lái)國(guó)內(nèi)外研究的一個(gè)熱點(diǎn)問(wèn)題[2]。

目前，國(guó)內(nèi)外對(duì)船體變形角采用的有效測(cè)量手段有光學(xué)測(cè)量法、慣性測(cè)量法、GPS測(cè)量法等。其中光學(xué)測(cè)量法使用光學(xué)設(shè)備對(duì)船體甲板變形角進(jìn)行實(shí)時(shí)監(jiān)測(cè)，測(cè)量精度高，理論精度能夠達(dá)到5角秒以?xún)?nèi)，測(cè)量結(jié)果可以近似為船體的實(shí)際變形[3]。但是光學(xué)測(cè)量法成本高昂，結(jié)構(gòu)復(fù)雜且實(shí)施困難，不能大規(guī)模使用。由于慣性系統(tǒng)體積小、精度高、隱蔽性好等優(yōu)點(diǎn)，使慣性測(cè)量匹配法成為目前最具有發(fā)展?jié)摿Φ难芯糠较颍渌枷胧峭ㄟ^(guò)在中心主慣導(dǎo)系統(tǒng)附近和局部戰(zhàn)位點(diǎn)附近分別安裝一套慣性系統(tǒng)，兩個(gè)慣導(dǎo)之間輸出的信息差能夠反映二者失準(zhǔn)角的大小，通過(guò)二者輸出的信息進(jìn)行動(dòng)態(tài)匹配實(shí)現(xiàn)船體變形的測(cè)量。

基于姿態(tài)匹配的船體變形測(cè)量方法最早由國(guó)防科技大學(xué)提出[4]，之后對(duì)激光陀螺的誤差進(jìn)行補(bǔ)償[5][6]以及對(duì)模型參數(shù)的辨識(shí)展開(kāi)了研究[7]。但是其采用的動(dòng)態(tài)變形角模型是非時(shí)變二階馬爾科夫模型，沒(méi)有考慮模型偏差帶來(lái)的誤差，而實(shí)際船體動(dòng)態(tài)變形模型復(fù)雜多變且慣性系統(tǒng)受到的噪聲不單一。針對(duì)變形角模型不確定的問(wèn)題，哈爾濱工程大學(xué)提出一種交互式多模型濾波的船體變形測(cè)量方法[8]，但是由于先驗(yàn)信息的不準(zhǔn)確使得狀態(tài)轉(zhuǎn)移概率很難定義，而且多次更新卡爾曼濾波方程需要大量的計(jì)算時(shí)間。文獻(xiàn)[9]提出一種基于姿態(tài)四元數(shù)匹配的神經(jīng)網(wǎng)絡(luò)船體變形測(cè)量方法，并對(duì)卡爾曼濾波中的時(shí)間延遲進(jìn)行了補(bǔ)償[10]，避免了歷史變形數(shù)據(jù)對(duì)實(shí)時(shí)變形影響導(dǎo)致的誤差。但是計(jì)算神經(jīng)網(wǎng)絡(luò)系統(tǒng)最優(yōu)參數(shù)需要大量的訓(xùn)練數(shù)據(jù)并且可能會(huì)導(dǎo)致過(guò)度學(xué)習(xí)。

基于多重漸消因子的強(qiáng)跟蹤卡爾曼濾波（Strong Tracking Kalman Filter，STKF）采用使殘差序列正交的方法確定最佳的多個(gè)漸消因子,在模型失配的情況下仍能很好地跟蹤狀態(tài)量的變化，該算法因有較強(qiáng)的魯棒性并且得到廣泛應(yīng)用[11]。在實(shí)際的船體變形測(cè)量中，由于環(huán)境的復(fù)雜性，慣性設(shè)備的誤差通常是各種噪聲的疊加，它們極少服從正態(tài)分布，有的幅值較大甚至還有奇異點(diǎn)。而傳統(tǒng)的卡爾曼濾波以最小均方誤差（MMSE）為最優(yōu)準(zhǔn)則，不能反映真實(shí)的噪聲情況，會(huì)產(chǎn)生較大誤差。最大互相關(guān)熵卡爾曼濾波以最大相關(guān)熵準(zhǔn)則（Maximum Correntropy Criterion，MCC）為最優(yōu)準(zhǔn)則，不僅能捕獲通常的二階統(tǒng)計(jì)信息，而且還可以獲得更高階的統(tǒng)計(jì)信息，因此能夠獲得更好的估計(jì)效果[12]。本文設(shè)計(jì)了一種強(qiáng)跟蹤最大互相關(guān)熵卡爾曼濾波（Strong Tracking Maximum Correntropy Kalman Filter，STMCKF）算法，與傳統(tǒng)卡爾曼濾波相比，當(dāng)模型不確定或存在未知干擾時(shí)，能夠更有效的估計(jì)船體變形角。

1 船體變形測(cè)量模型

船體變形測(cè)量系統(tǒng)由兩套慣性系統(tǒng)（Inertial navigation system，INS）組成，如圖1所示。在中心慣導(dǎo)附近安裝一個(gè)慣性系統(tǒng)（SINS1），局部戰(zhàn)位點(diǎn)安裝另一個(gè)慣性系統(tǒng)（SINS2），定義坐標(biāo)系分別為ox1y1z1和ox2y2z2，x軸沿著船體的右舷，y軸指向船艏方向，z軸與船體甲板平面垂直并指向上方。xyz構(gòu)成右手直角坐標(biāo)系，即為右前上坐標(biāo)系。

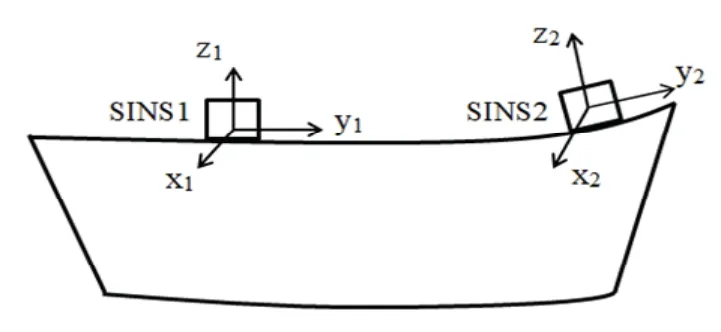
圖1 船體變形測(cè)量系統(tǒng)構(gòu)成Fig.1 Composition of hull deformation measurement system

令SINS1的載體坐標(biāo)系為b1，并選擇初始時(shí)刻t0的載體坐標(biāo)系b1作為SINS1的慣性坐標(biāo)系i1。同樣，令SINS2的載體坐標(biāo)系為b2，選擇初始時(shí)刻t0的載體坐標(biāo)系b2作為SINS2的慣性坐標(biāo)系i2。則表示i2系到i1系的坐標(biāo)變換矩陣，反映的是t0時(shí)刻的變形角。為系到b1系的坐標(biāo)變換矩陣，反映t時(shí)刻的變形角。由于陀螺偏移，導(dǎo)致解算出的慣性系與真實(shí)的慣性系i1，i2之間存在偏差，把解算得到的慣性系稱(chēng)為計(jì)算慣性系，簡(jiǎn)記為i1′，i2′。則根據(jù)坐標(biāo)系的定義，旋轉(zhuǎn)矩陣之間的關(guān)系為：

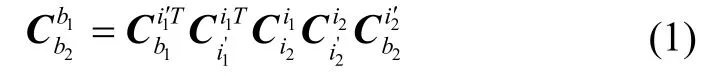
記t時(shí)刻的變形為φ=[φx,φy,φz]T，當(dāng)φ較小時(shí)，近似為：

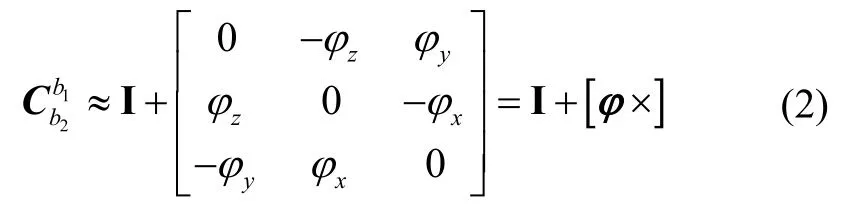
記t0時(shí)刻的失準(zhǔn)角為φ0=[φ0x,φ0y,φ0z]T，其包含有初始對(duì)準(zhǔn)誤差和初始變形角，當(dāng)φ0較小時(shí)，近似有：

記對(duì)應(yīng)的歐拉角分別為θi1和θi2，當(dāng)θi1和θi2較小時(shí)，近似有：

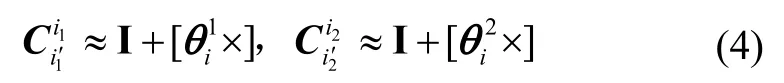
將式（2）（3）（4）代入（1），即得：

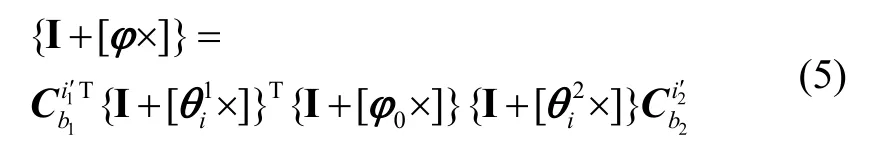
記和分別為：

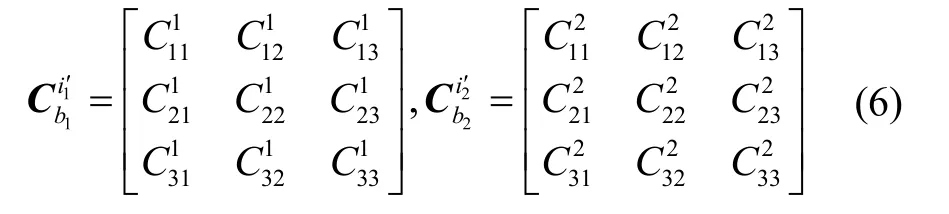
將式（6）代入式（5），根據(jù)矩陣兩邊的元素(1,2)、(3,1)、(3,2)相等分別建立等式，化簡(jiǎn)并忽略二階小量得到：

式中，矩陣Z和A由SINS1、SINS2的陀螺輸出和決定并隨其改變，具體表示為：

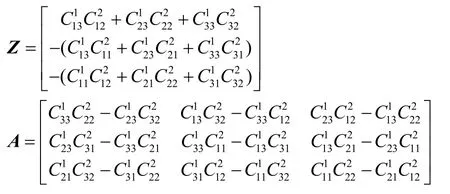
,θi2表示由陀螺漂移引起i′系與i系的偏差，慣性空間失準(zhǔn)角與陀螺漂移之間的關(guān)系為：

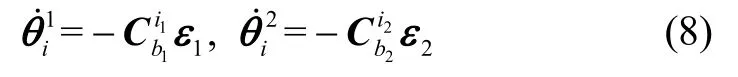
式中ε1、ε2分別為SINS1和SINS2的陀螺漂移。

根據(jù)船體變形頻譜分布的不同將其分為靜態(tài)變形和動(dòng)態(tài)變形[8]，其中靜態(tài)變形在短時(shí)間內(nèi)可以看作常值，動(dòng)態(tài)變形角滿(mǎn)足二階Markov過(guò)程，其模型為：

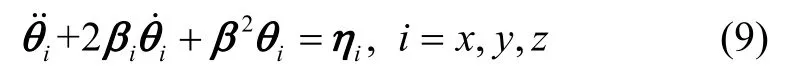
式中，βi是撓曲變形的模型參數(shù)，其大小與相關(guān)時(shí)間有關(guān)，具體表述為：

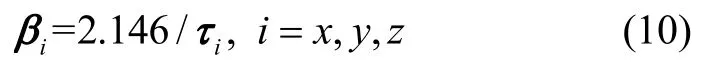
τi是船體變形的相關(guān)時(shí)間，ηi是白噪聲，其方差Qηi的大小為：

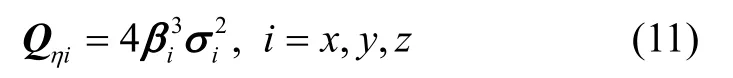
σi是動(dòng)態(tài)變形角θi的方差。

影響船體變形測(cè)量精度的一個(gè)主要因素是陀螺偏移，根據(jù)陀螺漂移的特性，一般將其分為隨機(jī)常值誤差和隨機(jī)游走誤差，分別建立模型為：

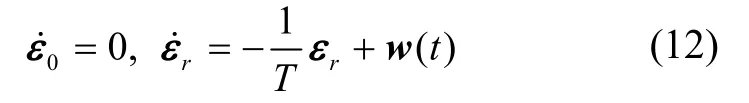
式中，w(t)～(0,σ2)，T為相關(guān)時(shí)間，由于相關(guān)時(shí)間很大，隨機(jī)游走誤差可以簡(jiǎn)化為：

選取系統(tǒng)狀態(tài)向量為18維，即：

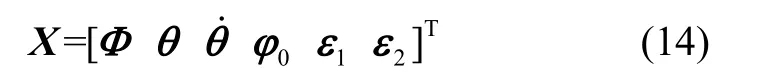
式中：Φ為靜態(tài)變形角，θ為動(dòng)態(tài)變形角，為動(dòng)態(tài)變形角速度，φ0為t0時(shí)刻的失準(zhǔn)角，ε1、ε2分別為SINS1和SINS2的陀螺漂移。

將式（7）中的Z作為觀測(cè)量，則系統(tǒng)的觀測(cè)方程可表示為：

考慮到φ=Φ+θ及式(8)，觀測(cè)矩陣可表示為：

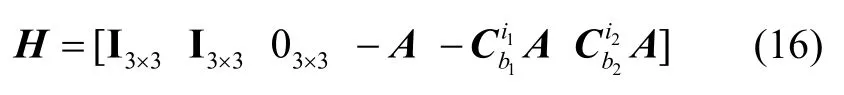
2 強(qiáng)跟蹤最大熵卡爾曼濾波算法

2.1 模型誤差對(duì)估計(jì)結(jié)果的影響

實(shí)際船體變形模型中，由于導(dǎo)致船體變形的因素復(fù)雜多變，沒(méi)有一個(gè)固定的形式，采用一個(gè)時(shí)不變的動(dòng)態(tài)變形模型必然會(huì)產(chǎn)生誤差。在先驗(yàn)估計(jì)中引入偏差項(xiàng)推導(dǎo)模型偏差對(duì)動(dòng)態(tài)變形角的估計(jì)誤差[13]，具體表述為：

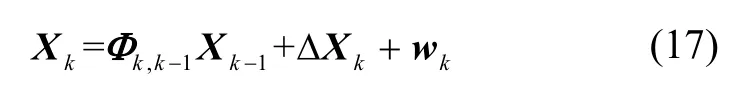
式中：ΔXk代表先驗(yàn)估計(jì)和真實(shí)狀態(tài)Xk的動(dòng)態(tài)模型偏差，代入卡爾曼濾波標(biāo)準(zhǔn)公式：

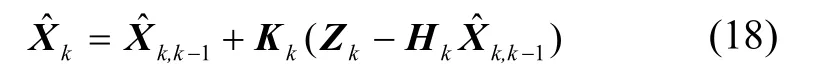
得到：

與式（18）相比，動(dòng)態(tài)模型偏差ΔXk導(dǎo)致的后驗(yàn)估計(jì)偏差為：

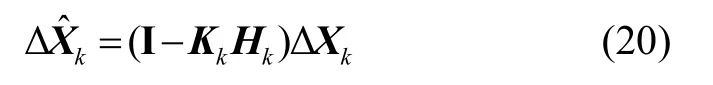
從式（20）可以看出，由ΔXk導(dǎo)致的估計(jì)誤差與增益矩陣K和觀測(cè)矩陣H是緊密相連的，如果在時(shí)變觀測(cè)系統(tǒng)中不考慮ΔXk導(dǎo)致的誤差，可能會(huì)對(duì)測(cè)量精度帶來(lái)較大誤差，甚至在有些特殊情況會(huì)導(dǎo)致系統(tǒng)不可觀測(cè)。因此，在進(jìn)行觀測(cè)更新之前，需要對(duì)模型偏差進(jìn)行修正。

2.2 多漸消因子強(qiáng)跟蹤濾波算法

傳統(tǒng)卡爾曼濾波具有記憶性，綜合利用了所有的量測(cè)值Zk，過(guò)去的量測(cè)數(shù)據(jù)會(huì)直接影響現(xiàn)在時(shí)刻狀態(tài)的估計(jì)精度，由于模型存在偏差，會(huì)使方差陣Pk不能正確反映狀態(tài)的估計(jì)精度，造成較大誤差。多漸消因子強(qiáng)跟蹤濾波通過(guò)對(duì)各數(shù)據(jù)通道以不同的速率進(jìn)行漸消，更準(zhǔn)確地調(diào)整增益矩陣，使系統(tǒng)具有較強(qiáng)的跟蹤能力。

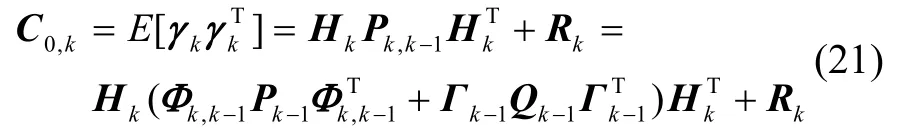
當(dāng)模型有偏差時(shí)，會(huì)使式（21）中等號(hào)兩邊不相等，導(dǎo)致新息方差矩陣失衡。為使式（21）等號(hào)兩邊相等，將Pk,k-1重寫(xiě)為：

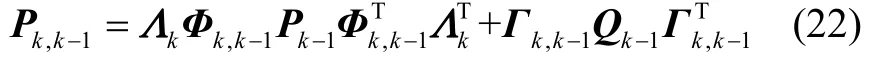
式中Λk=diag(λ1λ2…λk)表示狀態(tài)變量相應(yīng)的漸消因子組成的對(duì)角陣。

則式（21）可以重新表述為：

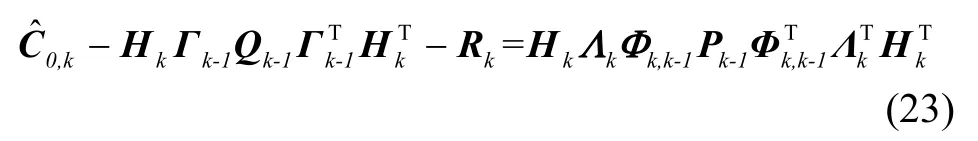
式中為k時(shí)刻新息序列γk的協(xié)方差矩陣估計(jì)值，可以根據(jù)式(24)進(jìn)行估算：

式中ρ為遺忘因子，0 ＜ρ≤1，通常ρ= 0.95。

進(jìn)一步，令

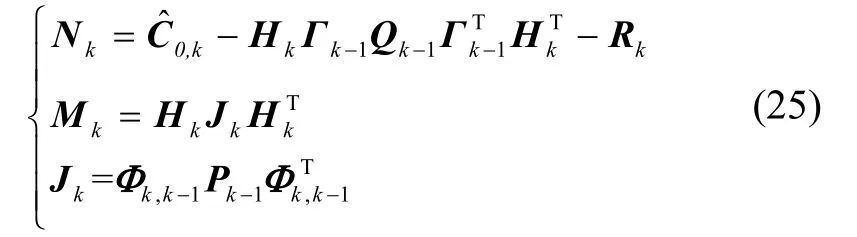
故可得

若Hk滿(mǎn)秩，即m=rank(Hk)，且Hk有j1,j2,…,jm共m列元素不全為0，則Mk可以簡(jiǎn)化為：

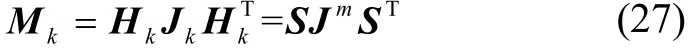
式中，S為Hk中不全為0的m列元素組成的矩陣，Jm為Jk中第j1,j2,…,jm行和第j1,j2,…,jm列元素組成的矩陣。

將式（27）代入式（26）并整理可得：

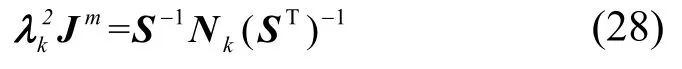
令βk=S-1Nk(ST)-1，因此多重漸消因子求法為：

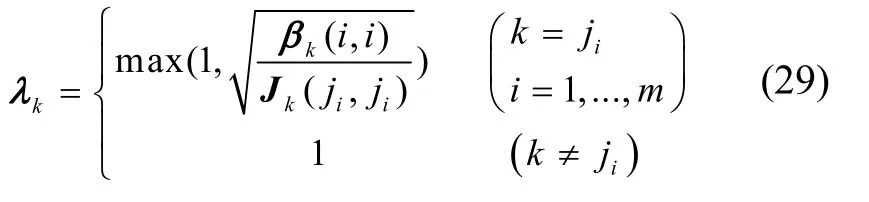
式中βk(i,i)和Jk(ji,ji)分別為矩陣βk和Jk的對(duì)角線元素值。

2.3 最大相關(guān)熵卡爾曼濾波

對(duì)于兩個(gè)服從聯(lián)合概率密度為FX,Y(x,y)的隨機(jī)變量X,Y∈R，其互相關(guān)熵定義為：

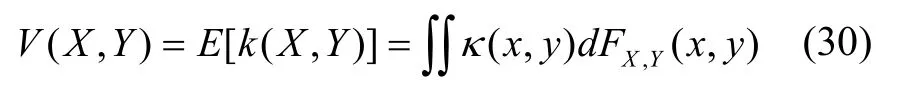
其中，E(·)表示求期望，κ(·)表示高斯核函數(shù)，即

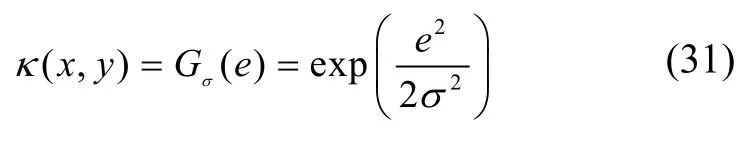
式中，e=x-y，σ＞ 0為核函數(shù)寬度。

將系統(tǒng)狀態(tài)方程和量測(cè)方程重新表述為：

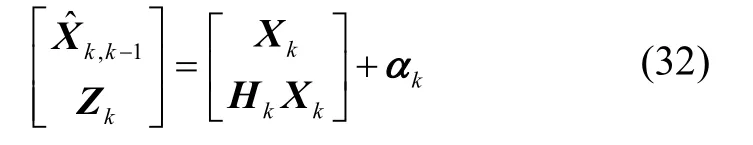
式中：

分別將Pk,k-1和Rk進(jìn)行Cholesky分解得到Bp,(k,k-1)和Br,k，則可得：

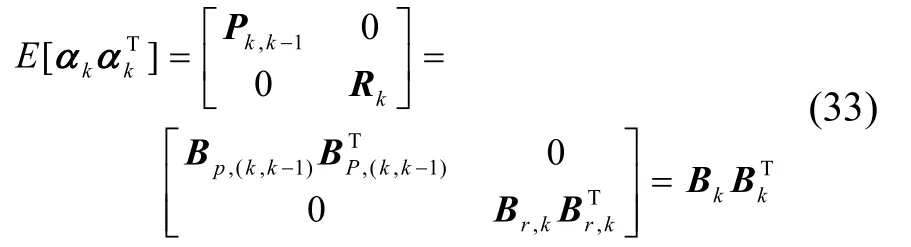
在式（32）左右兩邊同時(shí)乘，并重寫(xiě)為：

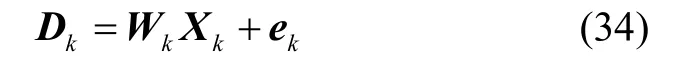
式中：

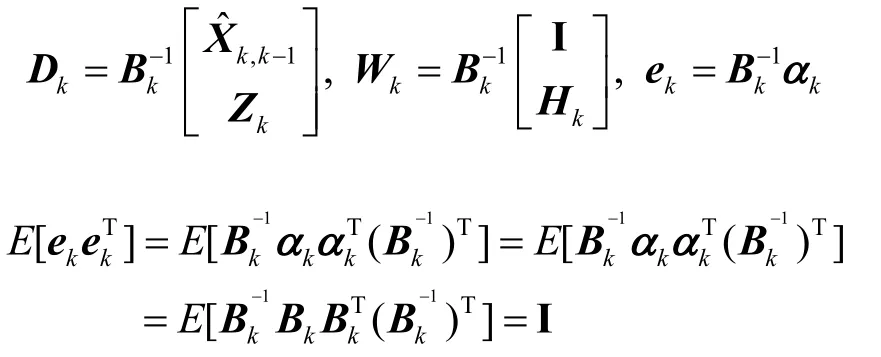
定義基于信息最大熵準(zhǔn)則下的代價(jià)函數(shù)為：

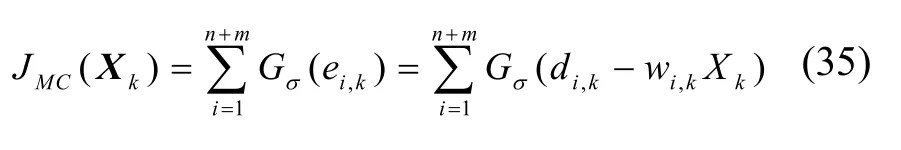
式中，n+m是Dk的維數(shù)，di,k和wi,k分別是Dk與Wk的第i個(gè)元素，Xk的最優(yōu)解可以通過(guò)使代價(jià)函數(shù)最大求得[14]，即

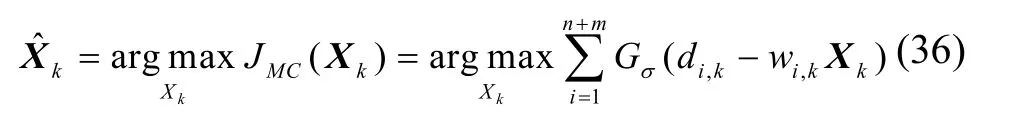
因此，可以通過(guò)式(38)得出Xk的最優(yōu)解：

求解式(28)可得

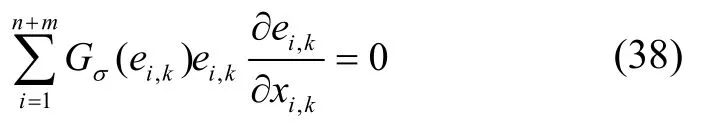
式中xi,k是Xk的第i個(gè)元素。

進(jìn)一步，定義：

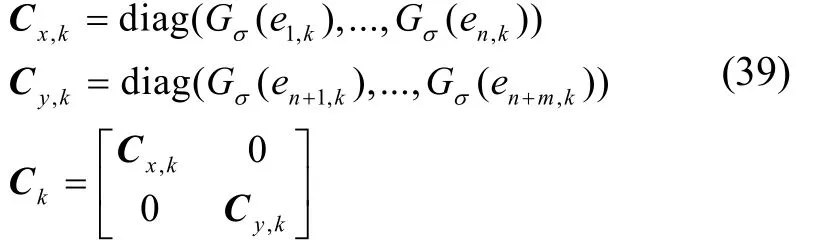
將式（38）寫(xiě)為矩陣形式為：

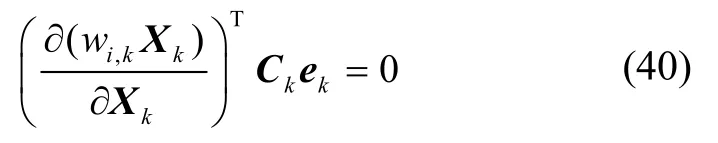
從式（40）可以看出，基于信息最大熵準(zhǔn)則的濾波方法利用Ck對(duì)誤差協(xié)方差重新加權(quán)并重新構(gòu)建量測(cè)信息，具體表述為：

3 仿真實(shí)驗(yàn)與結(jié)果分析

3.1 仿真條件

（1）艦船以10 m/s的速度勻速直線航行，以正弦規(guī)律繞橫搖軸、縱搖軸、航向軸作三軸搖擺，相應(yīng)的擺動(dòng)幅值分別為3 °、4 °、5 °，擺動(dòng)周期分別為10 s、8 s、6 s，隨機(jī)選取初始航向角為北偏東60 °，采樣頻率為100 Hz。仿真軌跡如圖2所示。

（2）認(rèn)為船體靜態(tài)變形角是常值，分別設(shè)置為0.2 °、0.1 °、0.05 °。船體動(dòng)態(tài)變形角為二階馬爾科夫隨機(jī)過(guò)程，變形角方差σ為5 ″、6 ″、7 ″，相關(guān)時(shí)間τ為1 s、1.5 s、1.8 s。

（3）SINS1、SINS2的陀螺常值漂移都取為0.05°/h,隨機(jī)游走誤差都取為

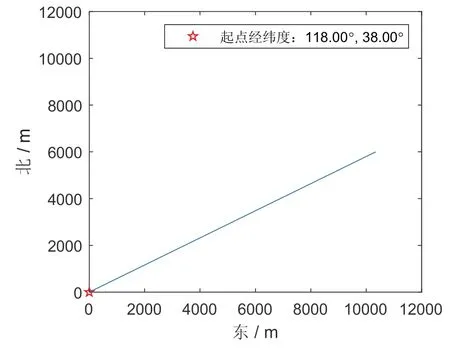
圖2 仿真軌跡圖Fig.2 Simulation trajectory

3.1 仿真結(jié)果與分析

設(shè)仿真時(shí)間為900 s，為驗(yàn)證本文提出算法的有效性，在三種環(huán)境下進(jìn)行仿真驗(yàn)證，環(huán)境設(shè)置如表1所示。

表1 三種環(huán)境設(shè)置表Tab.1 Three environment settings

在第一種情況中，假設(shè)在300～600 s的時(shí)間段內(nèi)，系統(tǒng)的真實(shí)噪聲變?yōu)?5Q，強(qiáng)跟蹤最大熵卡爾曼濾波和傳統(tǒng)卡爾曼濾波的變形角估計(jì)誤差如圖3～5所示。在第二種情況中，假設(shè)在300～400 s的時(shí)間段內(nèi)，系統(tǒng)的動(dòng)態(tài)變形角模型發(fā)生變化，將動(dòng)態(tài)變形角方差σ改為2σ，對(duì)應(yīng)的變形角估計(jì)誤差如圖6～8所示。在第三種情況中，假設(shè)慣性系統(tǒng)噪聲不是高斯白噪聲，而是重尾的混合高斯分布，SINS1、SINS2的隨機(jī)噪聲設(shè)置為：

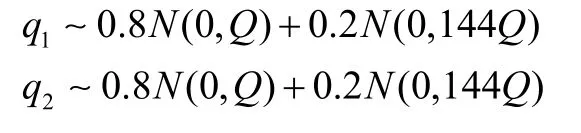
對(duì)應(yīng)的仿真結(jié)果如圖9～11所示。三種環(huán)境下的均方根誤差如表2所示（20 s之后穩(wěn)定求得）。

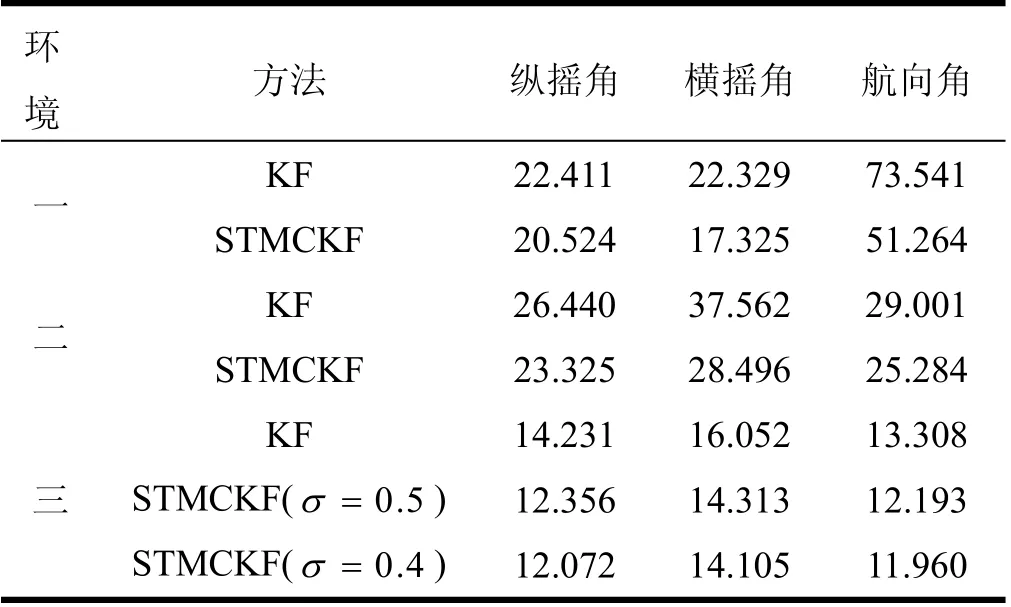
表2 變形角均方根誤差Tab.2 Deformation Angle root mean square error(")

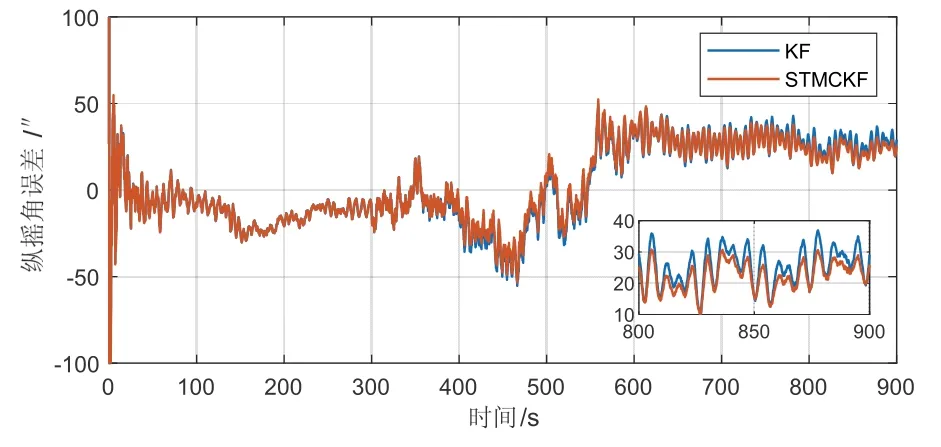
圖3 情況一縱搖角變形估計(jì)誤差Fig.3 pitching angle deformation estimation error in case-1

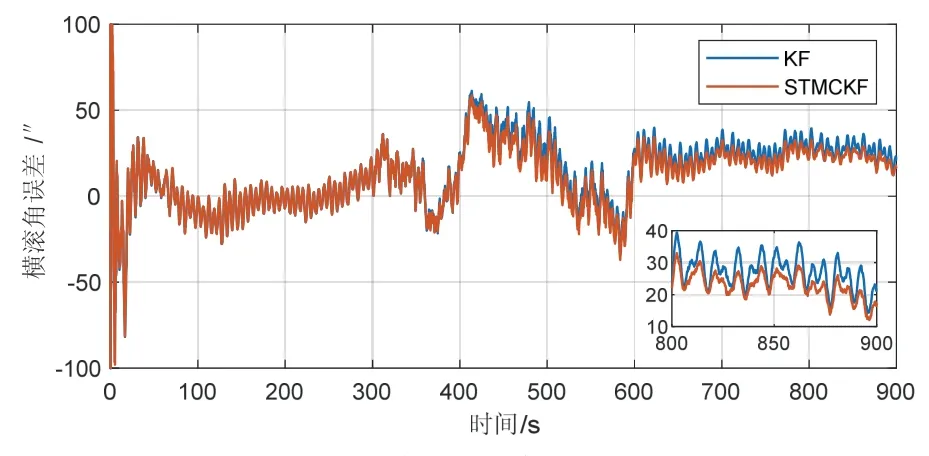
圖4 情況一橫搖角變形估計(jì)誤差Fig.4 rolling angle deformation estimation error in case-1

圖5 情況一航向角變形估計(jì)誤差Fig.5 yawing angle deformation estimation error in case-1

從圖3～5可以看出，在情況一中，當(dāng)系統(tǒng)噪聲突然變大時(shí)，變形角估計(jì)誤差變大，其中航向角誤差變化最大，強(qiáng)跟蹤最大熵卡爾曼濾波比傳統(tǒng)卡爾曼濾波的估計(jì)精度有明顯提高，尤其航向角最為明顯。結(jié)合表2數(shù)據(jù)，縱搖角、橫搖角和航向角的估計(jì)精度分別提高8.42%、22.41%和30.29%。由此可知，強(qiáng)跟蹤最大熵卡爾曼濾波可以更有效地跟蹤系統(tǒng)噪聲突變狀態(tài)，同時(shí)，由于系統(tǒng)噪聲突變和濾波器慣性等原因，導(dǎo)致600 s后傳統(tǒng)卡爾曼濾波航向角估計(jì)誤差出現(xiàn)一個(gè)偏置，但強(qiáng)跟蹤最大熵卡爾曼濾波的收斂誤差可以減少30.41″，使偏置減小。

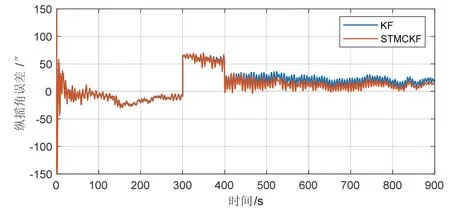
圖6 情況二縱搖角變形估計(jì)誤差Fig.6 pitching angle deformation estimation error in case-2

圖7 情況二橫搖角變形估計(jì)誤差Fig.7 rolling angle deformation estimation error in case-2

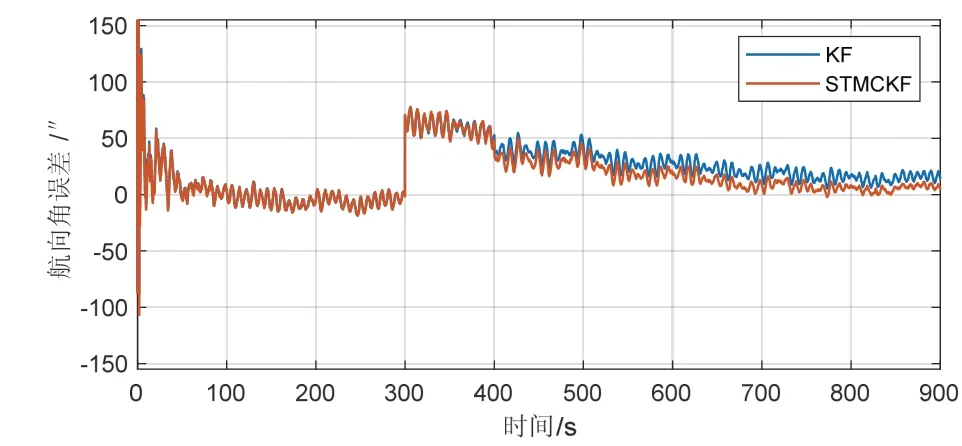
圖8 情況二航向角變形估計(jì)誤差Fig.8 yawing angle deformation estimation error in case-2

從圖6～8可以看出，在情況二中，變形角估計(jì)誤差在300s時(shí)有突變的現(xiàn)象，這是因?yàn)樵?00～400s的時(shí)間內(nèi)變形角模型突變使數(shù)據(jù)不連續(xù)導(dǎo)致的。結(jié)合表2數(shù)據(jù)，縱搖角、橫搖角和航向角的估計(jì)精度分別提高11.78%、24.14%和12.82%，由此可知，強(qiáng)跟蹤最大熵卡爾曼濾波比傳統(tǒng)卡爾曼濾波的收斂精度提高較大，說(shuō)明強(qiáng)跟蹤最大熵卡爾曼濾波提高了系統(tǒng)的魯棒性及環(huán)境適應(yīng)性。

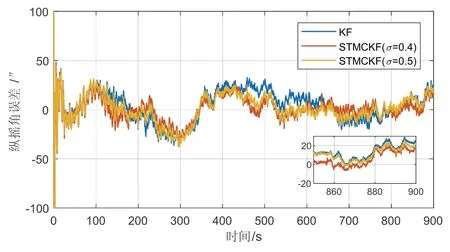
圖9 情況三縱搖角變形估計(jì)誤差Fig.9 pitching angle deformation estimation error in case-3

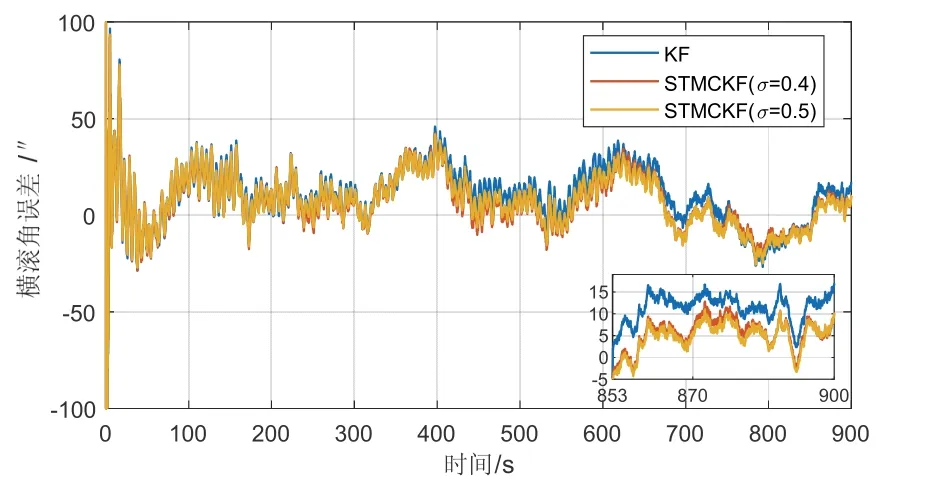
圖10 情況三橫搖角變形估計(jì)誤差Fig.10 rolling angle deformation estimation error in case-3

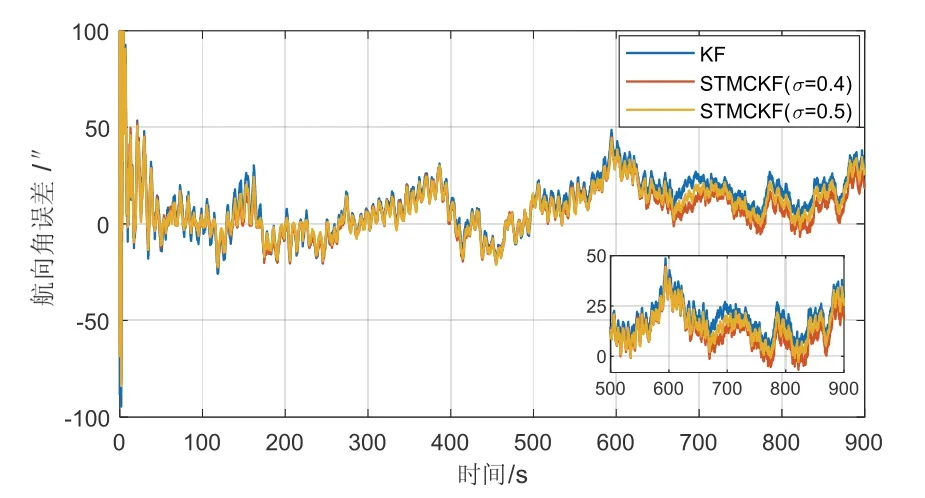
圖11 情況三航向角變形估計(jì)誤差Fig.11 yawing angle deformation estimation error in case-3

在情況三中，仿真試驗(yàn)設(shè)置的σ為0.4和0.5，從圖9～11可以看出，當(dāng)σ為0.5時(shí)，其效果比σ為0.4時(shí)更接近傳統(tǒng)卡爾曼濾波，這是因?yàn)棣以酱螅A誤差矩越占主導(dǎo)地位。結(jié)合表2數(shù)據(jù)，縱搖角、橫搖角和航向角的估計(jì)精度平均提高了14.17%、11.48%和9.25%，由此可知，當(dāng)慣性系統(tǒng)的噪聲為重尾的混合高斯分布時(shí)，通過(guò)調(diào)節(jié)核寬度σ，強(qiáng)跟蹤最大熵卡爾曼濾波比傳統(tǒng)卡爾曼濾波的估計(jì)精度明顯提高。

4 結(jié) 論

本文針對(duì)船體變形測(cè)量過(guò)程中模型不確定以及受未知噪聲干擾導(dǎo)致的誤差問(wèn)題，討論了模型偏差對(duì)濾波估計(jì)的影響，設(shè)計(jì)了一種基于姿態(tài)匹配的強(qiáng)跟蹤最大熵卡爾曼濾波算法。利用慣性系統(tǒng)輸出的姿態(tài)信息建立船體變形測(cè)量模型，以最大互相關(guān)熵為最優(yōu)準(zhǔn)則，不僅可以獲得二階誤差矩，還可以獲得更高階誤差矩。通過(guò)自適應(yīng)地調(diào)整多個(gè)漸消因子，即使在濾波達(dá)到穩(wěn)態(tài)時(shí)，仍然可以調(diào)整濾波增益。本文在三種環(huán)境下對(duì)該算法進(jìn)行仿真驗(yàn)證，仿真結(jié)果表明，相比較傳統(tǒng)卡爾曼濾波，強(qiáng)跟蹤最大熵卡爾曼濾波在模型不確定以及未知噪聲情況下能夠取得更好的效果，使其對(duì)復(fù)雜環(huán)境具有更好的適應(yīng)性，提高了系統(tǒng)的估計(jì)精度和魯棒性。