例談高考三角函數及解三角形問題的備考建議

胡能其

三角函數及解三角形是高中數學的主干知識,也是高考的必考內容.本文通過對近三年全國卷Ⅰ文科和理科試卷進行考點分析,歸納出常考知識點,并以高考真題為例總結每個考點的解題方法.

1 考點分析

1.1 2017—2019年高考全國卷Ⅰ考點分布

為了更清晰地歸納高考三角函數的考點,筆者整理了數學全國卷Ⅰ近三年的試題,得出表1.

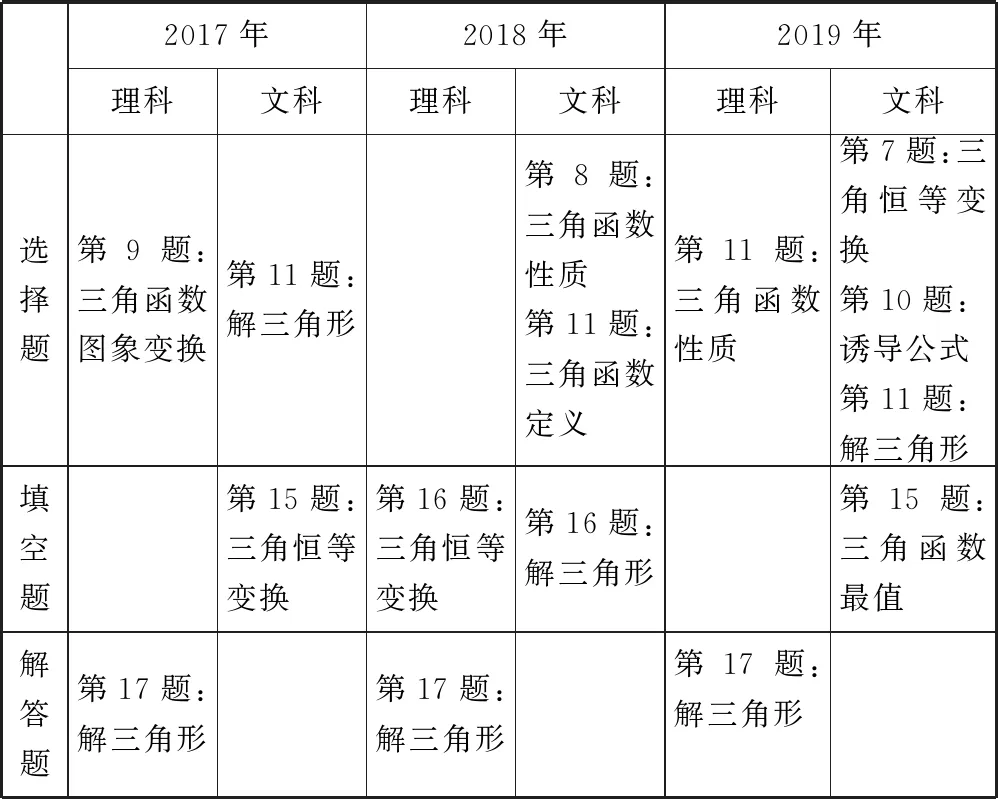
表1 全國卷Ⅰ近三年考點分布表

1.2 題型與分值

由表1不難發(fā)現,2017—2019年全國卷Ⅰ理科考查的題型均為一道小題和一道大題,大約17分,題型、分值相對穩(wěn)定;而文科考查的題型都是小題,但不管是分數值還是難度都有不同程度的提升.

1.3 主要考查內容

縱觀近三年全國卷Ⅰ文科和理科的主要考查內容，包括三角函數定義、三角恒等變換、三角函數圖象與性質、解三角形等.

2 典例剖析

2.1 任意角三角函數的定義

任意角的三角函數定義在高考中單獨命題雖然不是熱點,但也偶有考查,所以也要引起重視.

分析先由正切函數定義,得到a,b的關系式b=2a,再利用二倍角公式以及余弦函數的定義求得a的值,進而求得|a-b|的值.

2.2 三角函數的恒等變換

三角函數的恒等變換是歷年高考的一個必考點,主要考查三角函數的求值和化簡,考查學生對三角函數公式的正用、逆用及變形運用,難度中等.

1) 三角函數的求值問題

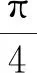
2) 三角函數式的化簡

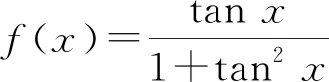
2.3 三角函數的圖象與性質

三角函數的圖象與性質是高考的熱點,經常以選擇題、填空題的形式出現,對考生綜合能力要求較高.

1) 三角函數的圖象變換

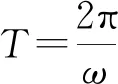
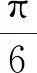
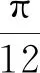
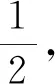
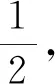
分析先利用誘導公式將函數“同名”化,然后利用圖象平移、伸縮變換分析即可.

2) 三角函數的性質

三角函數的性質主要包括三角函數的單調性、周期性、對稱性、最值等.解決三角函數性質問題主要是利用數形結合的思想、化歸思想和換元法進行求解.

A.f(x)的一個周期為-2π

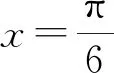
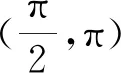
分析先求得f(x)的相關性質,然后再逐一檢驗,選出正確答案.

3) 三角函數的最值

三角函數最值問題主要有三種,一種是將三角函數轉化為y=Asin (ωx+φ)+h的形式,然后利用三角函數本身的有界性得出最值；一種是將三角函數最值問題轉化為求一元二次函數的最值；另外一種是利用導數研究最值.

A. 4 B. 5 C. 6 D. 7

分析先利用余弦函數二倍角公式和誘導公式,將函數轉化為以“sinx”為自變量的一元二次函數,然后利用一元二次函數求最值的方法求解.

2.4 解三角形

解三角形知識除了應用正弦定理、余弦定理以及面積公式外,往往還要結合三角函數相關公式.

(1)求A;

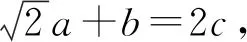
分析第(1)問先利用正弦定理將角的關系轉化為邊的關系,再用余弦定理求得角A的值;第(2)問則是先利用正弦定理將邊的關系轉化為角的關系,再利用三角恒等變換求得結果.