船體分段下胎封固支撐位置優化算法的研究
鹿 想,張雪彪,宋志鵬
(大連理工大學 運載工程與力學學部 船舶工程學院,遼寧大連 116024)
0 引言
在現代造船工藝中,分段建造完成之后,需要采用吊裝的方式將其放置在托架上,托架上布置鋼墩和木鍥等結構,將分段支撐起來,此道工序稱為下胎封固。圖1是下胎封固后的分段由盤車移運的過程,根據建造計劃的要求,盤車將分段連同托架運輸到合適的工位,開展后續的裝配工作。分段在下胎封固完成之后,由于分段在托架上由有限個支撐點支持,為了避免可能發生的變形,以及保證分段運輸過程中的穩定性,分段托架和支撐點的合理設計成為下胎封固設計中的關鍵環節。

圖1 盤車運輸分段實況圖
船體分段下胎封固工藝簡單,精度控制技術也相對粗糙,該工藝不僅對分段下胎后的預舾裝作業產生影響,而且由此產生的分段結構變形也會對后續的涂裝和裝配工藝帶來負面影響:1)由于分段放置在托架上,會增加預舾裝作業的施工難度,由于托架與分段之間的高度限制,導致部分舾裝件無法安裝,需要留待分段涂裝結束后在總組/合攏場地繼續施工,進而對船體涂裝也造成了破壞;2)下胎封固后如果有局部的變形會影響船體結構精度;3)下胎封固區域在分段涂裝時無法涂漆,其中以外板為胎的雙斜切類型分段受影響最大,需要考慮如何在不影響船體結構精度和分段下胎后預舾裝工作的前提下,優化下胎封固工藝及工裝設備,以減少下胎封固工藝對船體涂裝的影響。
在實際的工藝設計過程中,船廠設計人員一般都是根據經驗來進行分段的下胎封固方案設計,很少有人專門研究這些問題;其中分段下胎封固工藝所導致的船體結構局部變形會影響分段結構精度,這主要與下胎封固點的選擇密切相關,封固點的選擇與分段吊裝工藝中吊點的選擇有相似之處,都是為了減少變形、提高結構的穩定性。吳仲其等[1]提出了船舶分段吊裝的工藝要求和注意事項,芮曉松等[2]基于有限元仿真軟件建立15 000 DWT化學品船機艙分段的弱框架結構有限元模型,在計算過程中僅考慮重力,以施加慣性載荷的方式計算得到該分段在吊裝翻身過程中最大拉應力和最大剪應力,為求解下胎封固過程中的分段變形可以提供參考。林少芬[3]將最小眼板數量作為優化目標,驗證了粒子群算法求解船舶分段吊裝方案設計問題的可行性;李瑞等[4]對船舶分段吊裝方案設計系統進行了研究,引入粒子群優化算法,并借助MATLAB和ANSYS軟件的數據交互,實現吊點位置的最優化設計,這些研究將優化算法引入了吊裝的方案優化中。
目前下胎封固支撐點的設計還沒有成熟的算法,本文主要研究下胎封固支撐點的設計,基于工程經驗,本文確立了分段下胎封固的一般工藝要求和工藝原則,下胎封固支撐點的計算選用隨機行走優化算法,利用MATLAB軟件進行編程實現,其中的結構變形計算模塊則通過ANSYS軟件進行計算,最后以一個雙層底分段為例進行了算法驗證,初步實現了下胎封固方案設計的自動化。
1 船舶分段建造下胎封固工藝簡述
1.1 下胎封固結構介紹
圖2為某船上甲板分段下胎封固方案設計圖,為了避免結構變形,在分段上端設有局部的臨時加強槽鋼。船體分段有平面分段和曲面分段,平面分段形狀規則,重心較低,下胎封固比較簡易。對于曲面分段,需要綜合考慮重心以及運輸過程中的穩定性等因素,封固工藝相對復雜。下胎封固方案設計要結合不同分段的特點,本文旨在開發支撐點設計的優化算法,研究對象主要是結構相對簡單的平面雙層底分段。
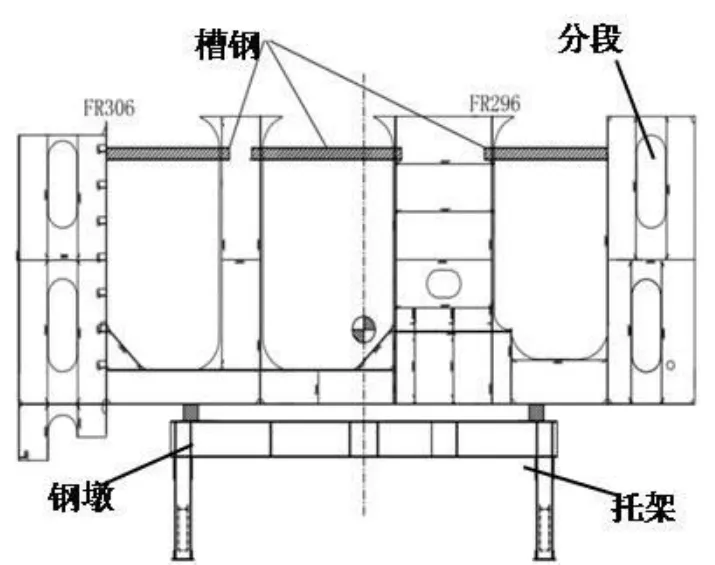
圖2 某分段下胎封固設計圖
1.2 支撐結構簡述
托架與分段之間的支撐結構有:1)方形鋼墩,尺寸為300 mm×400 mm×400 mm,鋼墩與分段之間的接觸面墊有膠皮;2)對扣槽鋼,對于特殊的曲面分段,將槽鋼與分段焊接在一起,保證其穩定性,一般采用28A槽鋼對扣焊接的方式。支撐位置一般設置在強力構件交叉點處。
托架對整個分段起承載作用,采用2個托架進行支撐。托架和分段的總重量不能超過盤車運輸時候的承載力,托架位置設置在強力連續構件下方。某船廠常用的托架規格類型有承載能力為100 t、60 t、40 t、20 t這4種,各型號托架的主要區別是承載力,所以分段的重量是影響托架型號選擇的主要因素。在布置托架時要考慮運輸盤車的載荷分布曲線,盤車中間區域的承載能力較強,托架應放置在中間區域。
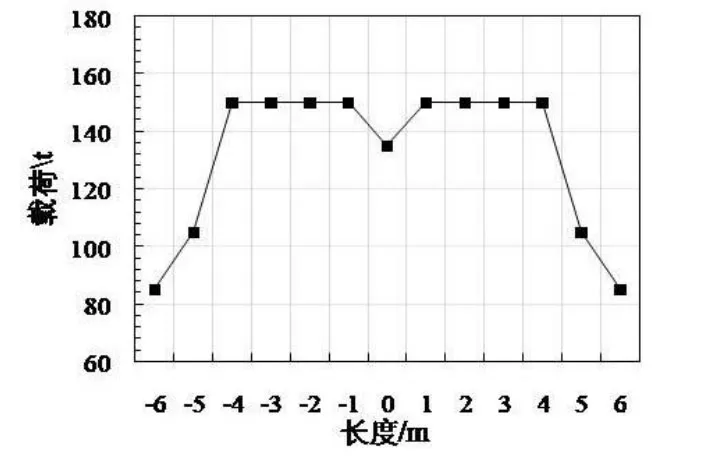
圖3 盤車載荷分布圖
在下胎封固過程中,主要的目標有2點:1)結構在擺放和運輸過程中的穩定性與安全性;2)減小分段在擺放和運輸過程中的變形。因此,下胎封固工藝的一般原則如下:
1)2個托架對稱于重心分布,擺放方向視分段長寬而定。
2)托架盡量擺放在強力連續結構的正下方。
3)支撐結構成對布置,每對槽鋼或鋼墩對稱于分段重心與托架中心分布。
4)支撐位置盡量避開可能碰到的結構和開口等。
5)考慮穩定性的影響,支撐工具(托架、鋼墩)不宜太過靠近分段重心。
2 分段下胎封固支撐點優化算法設計
本節建立了雙層底分段模型的下胎封固方案數學優化模型,描述優化算法的實現過程,使用改進的隨機行走法進行求解,得出優化的下胎封固支撐點方案。
2.1 下胎封固方案優化模型的建立
以直線代表分段橫縱向的結構,縱向結構數量為a,橫向結構數量為b,經過映射形成網格線。如圖6所示,網格上的點即為橫縱向結構交叉點,可以作為鋼墩支撐點的備選位置。為了找到最優的支撐點方案,建立如下優化模型:
1)目標函數f(x)
以分段支撐之后的最大變形f(x)最小為目標函數,即下胎封固之后使分段的變形最小為優化目標。
2)設計變量x
設計變量x(i,j)為各支撐點的位置編號,不同的x對應不同的鋼墩支撐方案;i代表支撐點所在的橫向構件編號,j代表縱向構件編號。
3)約束條件
根據下胎封固的工藝原則,支撐結構不能靠近分段中心,因此托架上某個鋼墩位置的可選方案如圖4所示黑框內的n個點,優化算法可以就這個鋼墩位置進行計算,其他3個鋼墩根據重心對稱原則確定,這樣形成n種支撐方案,將n種支撐方案進行編號。根據不同方案下的分段最大變形量,從而得出最優支撐方案。因此約束條件為:1≤x≤n,x∈N*,N*為正整數;i、j的約束條件根據分段的橫縱構件個數來確定,1≤i≤b,1≤j≤a。
綜上所述,本研究中下胎封固問題的最優化模型如下:
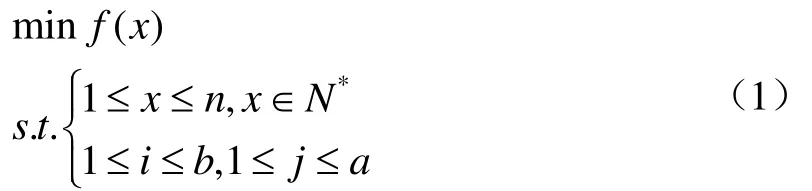

圖4 分段結構映射網格圖
2.2 應用隨機行走法優化支撐點位置
隨機行走法在給定初始點的前提下,在給定的以步長為半徑的范圍內,通過生成隨機數的方式不斷比較迭代,找到最優解。文獻[5]給出的隨機行走法可以用來解決全局最優化問題[5],隨機行走法操作簡單,不容易陷入局部最小值,將隨機行走法進行改進,迭代過程中隨機生成3個新的支撐位置而不是1個,可以進一步提高全局尋優的能力,對初始值的依賴也進一步降低。
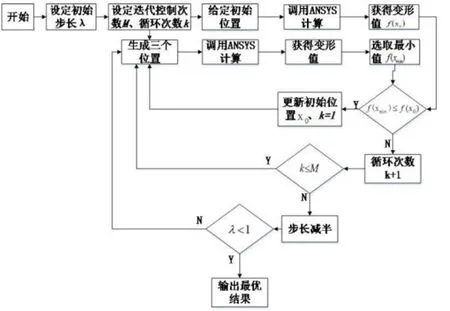
圖5 支撐點優化計算流程圖
在確立了優化模型之后,本文采用改進的隨機行走法進行鋼墩位置的自動優化,隨機行走法適合這種組合優化問題,找出全局最優解;在實際計算時并不需要對每個可選方案都進行計算,而只需要對迭代過程中涉及的支撐點方案進行迭代尋優,大大減少了計算量。圖5是支撐點優化計算的流程圖,采用改進的隨機行走法,初始迭代點x0行走尋優的過程如下:
1)程序開始,設置初次行走步長λ=3。
2)設置迭代控制次數M=3,并用變量k記錄循環次數,k設初始值為1,k≤3。
3)給定鋼墩的初始位置,將鋼墩的初始支撐位置設在分段靠近中間的區域,這也符合下胎封固方案設計的實際情況,然后開始尋找更優的支撐點。
4)調用ANSYS計算初始位置的變形,讀取分段結構的最大變形值δmax,并傳遞回MATLAB優化控制算法程序中作為目標函數值,即令f(x0)=δmax。在調用ANSYS計算過程中,將各方案的計算結果保存,如果有重復計算的方案,直接從保存結果中獲取。
5)在初始位置以步長λ為半徑的范圍內隨機生成 3個新的支撐位置x1、x2、x3,即生成了新的 3組支撐方案,然后調用ANSTYS計算這3組支撐方案的最大變形量,即獲得f(x1)、f(x2)、f(x3)的值。將f(x1)、f(x2)、f(x3)進行比較找到3組方案中的變形最小值,記為f(xmin),并將最小值的支撐點記為xmin。
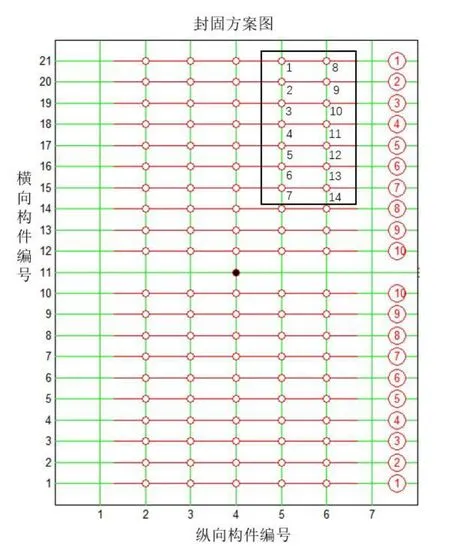
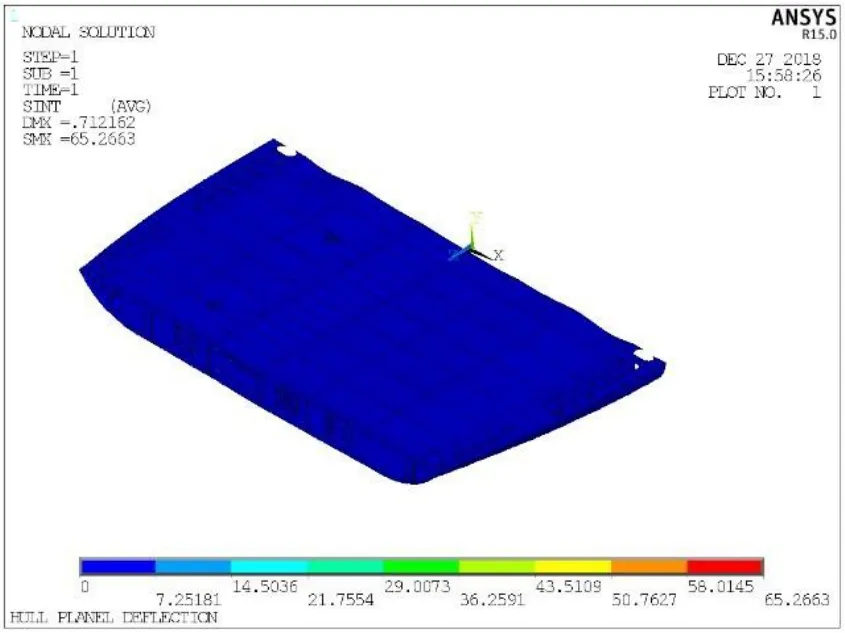
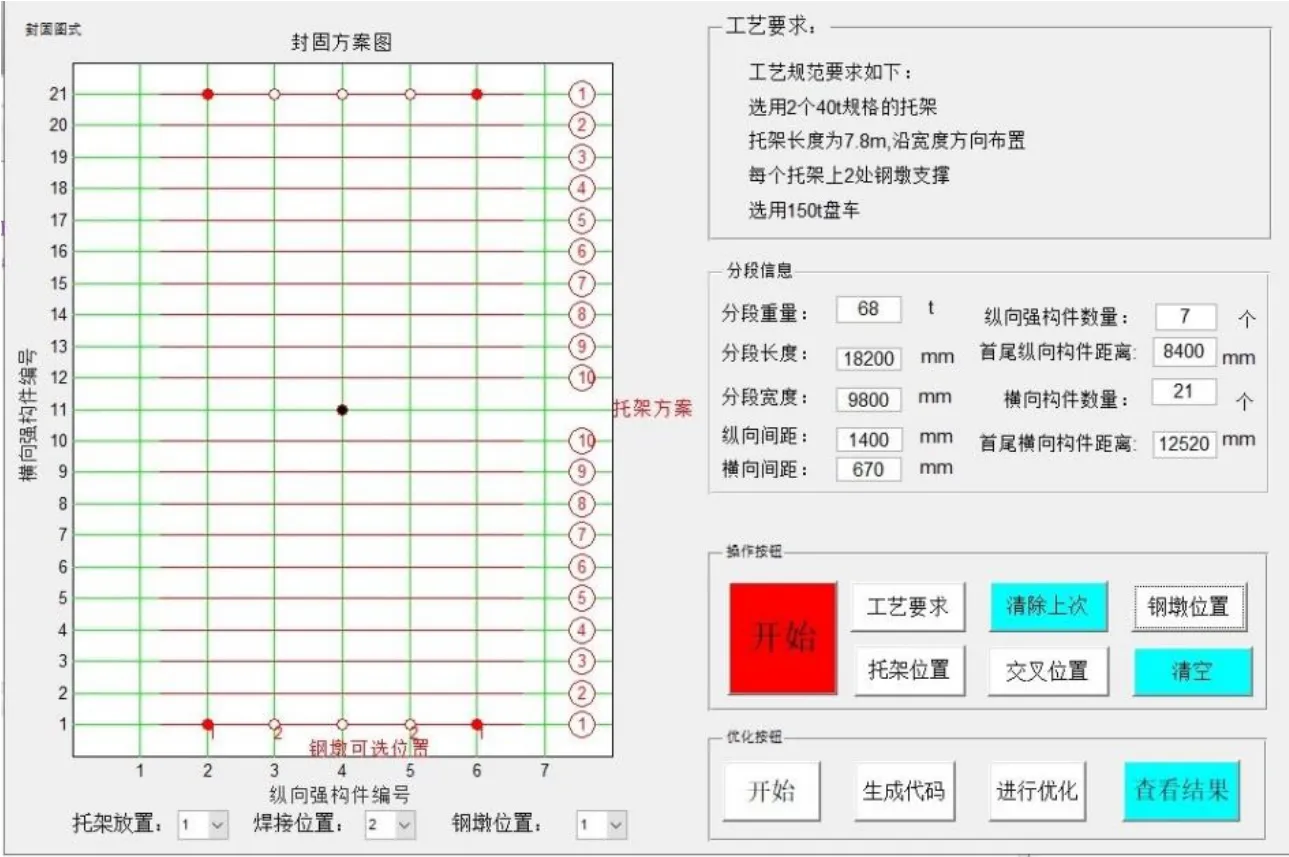
6)將f(xmin)與f(x0)進行比較,如果f(xmin) 7)判別循環次數k≤M,如果是Y,則返回5)處,繼續迭代計算過程;如果是N,將尋優范圍縮小一半,即把步長λ減半,返到5)處,再次以此步長為基礎生成3個位置,開始新一輪行走。當步長λ<1時程序停止,此時輸出最終的最優解xmin以及f(xmin),這就是最佳的鋼墩支撐位置與變形量。 本節以某船102分段為例,分析其結構特點,結合下胎封固工藝原則,對某船型102雙層底分段的下胎封固方案進行分析,并應用前文所述支撐點優化算法進行支撐點優化。 圖6為某船102雙層底分段的結構簡圖,該分段總重為68 t,其重心位于距中心線32 mm的左舷一側,縱向位置為FR46+483 mm,垂向位置為內底面下方567 mm處,重心大致位于分段平面的幾何中心。強力橫向結構分別為FR40、FR42、FR44、FR46、FR48、FR50和FR52。其中FR46為艙壁,其余為帶孔的連續肋板。長度方向,縱骨間距靠近中心線部分為560 mm,其余部位為670 mm。在中心線處及距離船中2 240 mm處有連續水密艙壁,在距離中心線4 920 mm和7 600 mm處有強力縱桁。 1)托架的可選方案 根據102分段的重量,選擇2個40 t型號的托架。此型號托架高1 800 mm,長7 800 mm。托架的位置可以放置于縱桁和縱骨的正下方,左右舷各放置1個。分段最大寬度18 200 mm,長度為9 800 mm,托架沿長度方向放置,如圖6所示。 2)支撐點可選方案 102分段為重心較低的平面分段,采用鋼墩支撐的方案。每個托架上設2個鋼墩,共計4個鋼墩,對稱分布于重心。根據此前的托架位置,鋼墩的位置選在縱桁或縱骨與肋板的交叉點處。如圖7所示,將肋板重新編號為 1-7,將縱骨或縱桁重新編號為1-21。除去4號肋板與8-15號縱桁,鋼墩的位置可以選在其余肋板與縱桁或縱骨的交叉點處。根據對稱原則將支撐點進行組合,一共可以得到14種方案。為了得到最合適的下胎封固方案,有必要進行優化計算。 圖6 102分段結構簡圖 根據圖6所示102分段結構,以直線代表分段橫縱向的結構,經過映射形成網格線。如圖7所示,網格上的點即為橫縱向結構交叉點,可以作為鋼墩支撐點的備選位置。 程序設置隨機行走法的步長為 3,采用優化程序計算,其間調用ANSYS進行計算7次,得到9號鋼墩位置方案最優,對應于左右舷距分段距中心線4 920 mm縱桁與FR42、FR52的交點,最大變形值為0.71 mm。 本文采用ANSYS軟件建立102分段的有限元模型,如圖7所示,坐標軸原點位于分段艏部中心線處。應用 SHELL63單元模擬分段中的鋼板,BEAM188單元模擬縱骨,彈性模量設為2.06×1011Pa,泊松比為0.3,慣性載荷取為9.8 m/s2。 圖7 102分段結構簡化模型圖 最優方案變形如圖8和圖9所示,變形最大處位于坐標原點的艏部開口位置,最大變形為0.71 mm,此變形量相對于整個分段來講非常小,對分段結構的運輸及合攏裝配等不會產生影響。最大應力位于肋板開口處和支撐點處,最大應力為65.3 Mpa,整體分段沒有大的應力集中區,且應力水平較低,結構不會發生屈曲變形。 本文采用隨機行走法對某雙層底分段的下胎封固方案進行優化,計算結果較好。為了適應不同分段進行下胎封固方案的計算要求,應用 MATLAB軟件開發了分段下胎封固方案優化的計算程序,相關的功能模塊都集成到程序GUI界面中。圖10為下胎封固方案選擇界面,將分段信息輸入對應的文本框,點擊對應按鈕,右上方則輸出對應的工藝要求,左側的封固方案圖顯示托架和鋼墩的推薦方案。在優化完成之后,界面會彈出提示框。點擊查看結果,可以進入下胎封固方案結果顯示界面,如圖11所示。可以在右上方顯示各個支撐點的坐標,并顯示優化方案的分段結構最大變形值,在界面左側顯示分段變形、應力等云圖。 圖8 102分段最優方案垂向變形云圖 圖9 102分段最優方案應力云圖 圖10 下胎封固方案選擇界面 圖11 下胎封固方案結果顯示界面 本文基于船廠下胎封固工藝的一般原則,以結構變形量最小為優化目標,采用隨機行走法對封固支撐點進行了優化,并以某船102分段為例,設計了分段的下胎封固可選方案,包括托架的方案和支撐點的優選方案,優化結果表明基于隨機行走法的下胎封固支撐點優化算法是可行的。目前,本算法適用于一般的船體雙層底分段,未來結合船廠Tribon軟件所建立的分段模型,可以開發各種分段下胎封固方案計算的程序,為船廠提供下胎封固工藝優選方案。3 某船102分段下胎封固方案的分析
3.1 某船102分段介紹與分析
3.2 下胎封固過程中支撐工具的可選方案
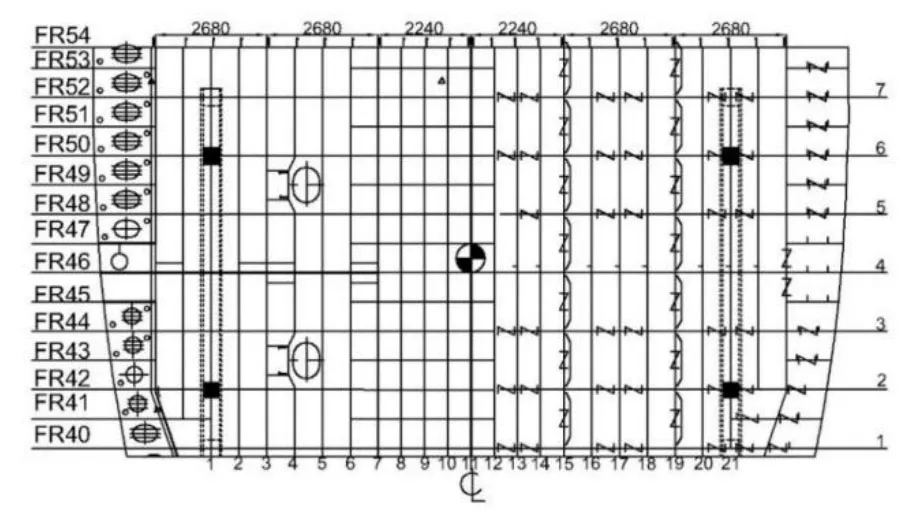
3.3 支撐點優化及結果分析
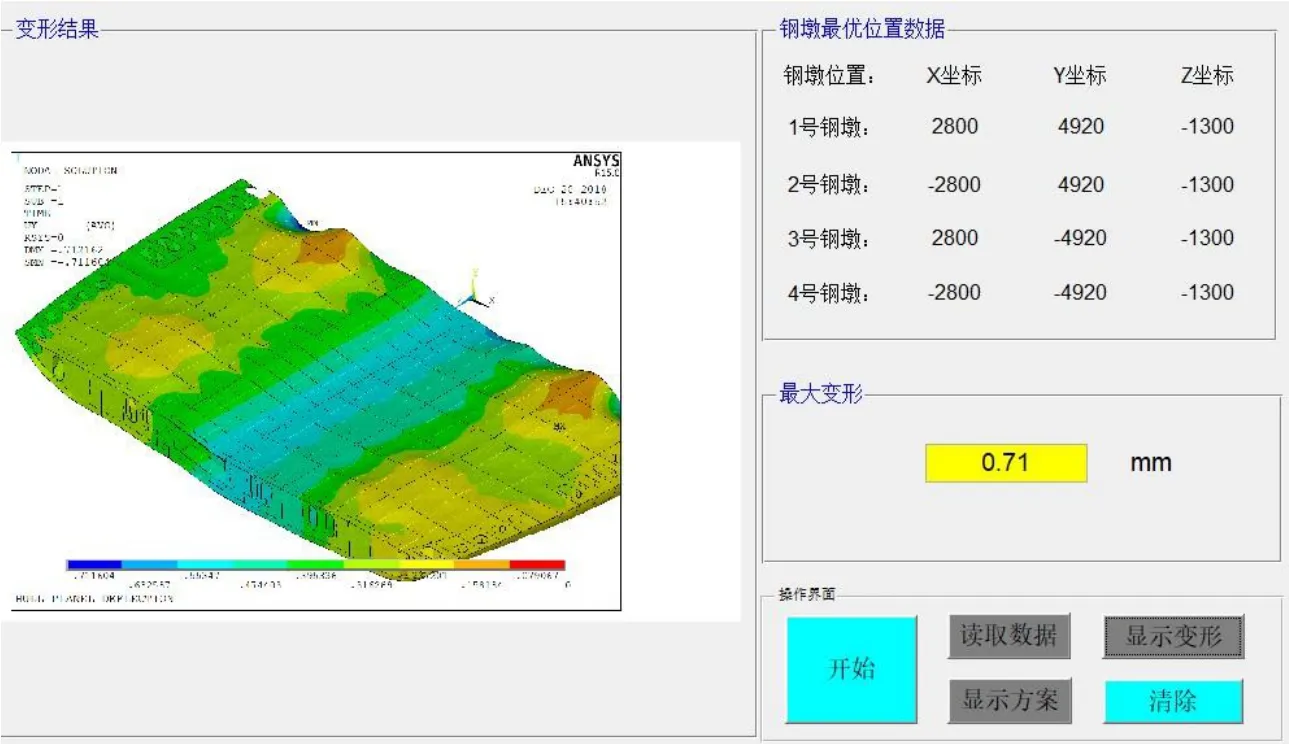
3.4 優化程序可視化界面開發

4 結論

