近壁面網格尺寸對風力機翼型數值計算結果影響研究
趙安安,李有恒
(1.魯能新能源(集團)有限公司甘肅分公司,甘肅 蘭州 730070;2.國家電力投資集團北京電力有限公司,北京 102300)
1 引言
目前,采用風力機發電是利用風能的主要形式,風輪作為風力機吸收風能的主要部件,其空氣動力學性能決定了風力機吸收風能的效率,翼型的氣動性能分析是研究風力機風輪氣動特性的基礎。研究者采用風洞實驗和數值模型方法分析了翼型的氣動載荷[1,2]、噪聲特性[3,4]和結冰對翼型氣動特性的影響規律[5]。風洞實驗研究雖然可靠,但實驗方法受實驗條件、成本和周期等因素的限制。隨著計算機水平的不斷發展,數值模擬方法成為風力機翼型性能分析的重要手段,但數值計算結果受網格尺度、湍流模型等因素的影響。文獻[6,7]研究表明,近壁面網格尺寸對湍流數值計算結果比較敏感。
本文在雷諾數Re=3.0×106的條件下,以NACA4415翼型為研究對象,分析數值模擬中翼型近壁面網格尺寸對其升阻力系數和表面壓力特性的影響規律,為提高風力機翼型數值模擬的準確性提供參考。
2 計算模型
以具有實驗數據的NACA4415翼型為研究對象,翼型的外形如圖1所示,數值計算中,翼型的弦長c為1 m。

圖1 NACA4415翼型外形
3 計算域及網格劃分
計算域如圖2所示,由半圓區域和矩形區域組成,半圓ABC距翼型尾緣的距離為20 c,尾緣距邊界AE、CD的垂直距離均為20c,距邊界DE的垂直距離為40 c。
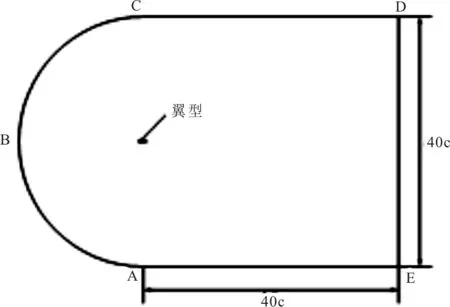
圖2 計算域示意
采用結構化網格對圖2的計算域進行網格劃分。為了提高數值計算精度,對翼型周圍的網格進行加密處理,網格示意圖如圖3所示。為了分析翼型近壁面網格分布對數值計算結果的影響,考慮了近壁面第一層網格高度和翼型弦向節點分布個數,采用了3種網格劃分方式,具體的網格劃分策略如表1所示,通過比較case1和case2的計算結果,分析翼型弦向節點個數對計算結果的影響;比較case2和case3的計算結果,分析翼型法向的第一層網格高度對計算結果的影響;結合3種不同的網格劃分方式,分析翼型法向的第一層網格高度和網格的縱橫比對翼型氣動性能的影響。

圖3 網格示意
4 數值計算方法及邊界條件
翼型流場的數值求解中,控制方程為不可壓縮的連續性方程和雷諾時均的N-S方程:
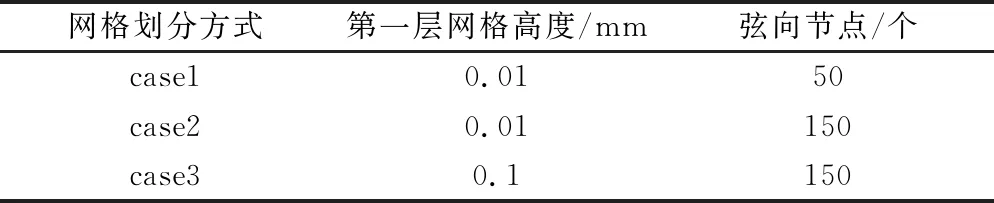
表1 網格劃分策略

(1)
(2)
式(1)、(2)中:t為時間;ρ為空氣密度;p為表面壓力;v為速度矢量;τ表面應力矢量;f為單位質量體積力矢量。
基于Fluent軟件求解方程,所有方程采用二階迎風格式離散;采用SIMPLEC算法耦合速度和壓力;選用k-ω SST湍流模型;計算區域入口為速度入口,出口為壓力出口,靜壓設置為0 Pa。
5 結果分析
翼型法向的第一層網格高度決定了y+的分布規律,進而影響數值計算結果。圖4為3種網格劃分方式下,雷諾數Re=3.0×106時,計算得到的翼型表面y+沿弦向方向的分布規律,由圖4可知,case1和case2算例計算得到的y+小于1,case3算例計算得到的y+大于1。
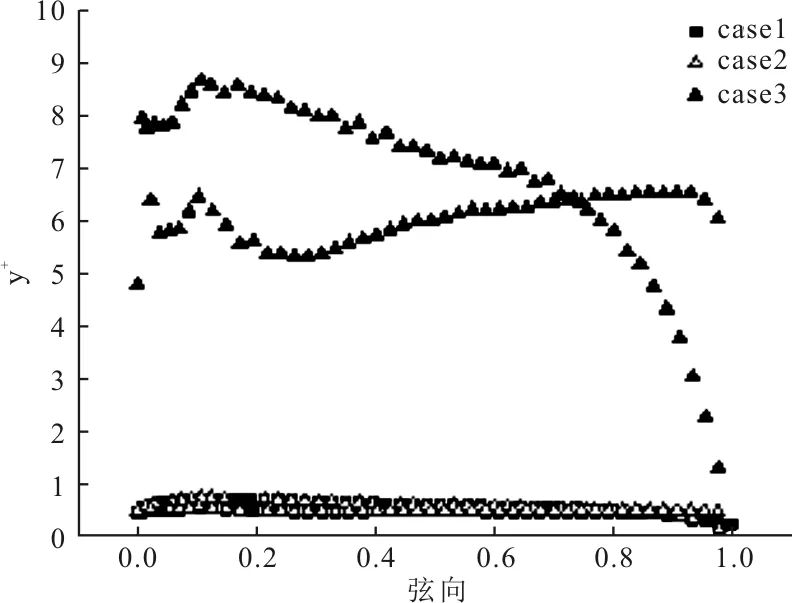
圖4 y+沿弦向方向的分布
5.1 升阻力系數
為了驗證翼型近壁面網格劃分的合理性,在上述3種網格劃分方式下,分別計算得到不同攻角下翼型的升力系數和阻力系數,并與實驗結果比較,結果如圖5和圖6所示。由圖5和圖6可知,case1、 case2和case3的計算結果相比,不論是升力系數還是阻力系數的變化趨勢,case2的計算結果更加接近實驗值,說明翼型第一層網格相同的情況下,弦向網格節點分布對計算有明顯影響,且大攻角下的影響更明顯。同時,翼型弦向網格節點分布相同的情況下,翼型第一層網格尺寸越小,計算結果更接近實驗值。綜上所述,翼型第一層網格高度應滿足y+小于1的要求;同時,弦向的網格節點越多,即網格的縱橫比越小,計算結果越接近實驗值。
5.2 表面壓力
翼型的表面壓力差是風力機葉片氣動力的來源,因此,數值計算中對翼型表面壓力的準確預測有利于提高葉片載荷計算的精度。文中比較了3種網格劃分方式下,攻角為-5°、0°、5°和15°時,翼型表面壓力的分布趨勢,結果如圖7所示。由圖4和圖5可知,case2的計算結果接近實驗值,因此,以case2計算得到的表面壓力為基準,分析翼型近壁面網格尺寸變化對其表面壓力分布的影響。比較圖7的計算結果可知,攻角為-5°和15°時, case1的結果與case2的結果偏差較大,說明弦向網格節點變化對翼型表面壓力的敏感,特別是翼型靠近前緣的位置。比較圖7還可以看出,大攻角下翼型近壁面網格分布對表面壓力的影響較大。即翼型近壁面網格的縱橫比越小,計算得到的表面壓力更準確。

圖5 升力系數隨攻角的變化
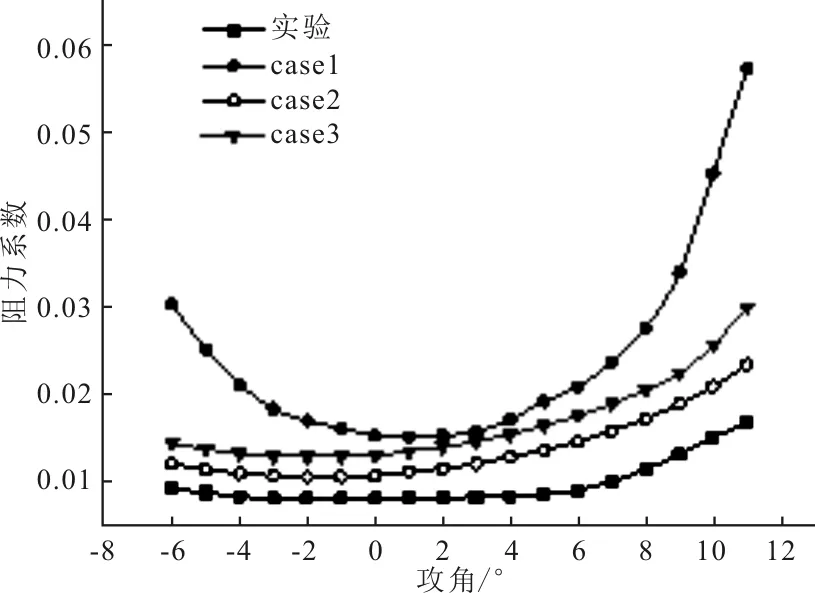
圖6 阻力系數隨攻角的變化
6 結論
本文以NACA4415翼型為研究對象,在雷諾數Re=3.0×106的條件下,分析了翼型數值模擬時近壁面網格尺寸對其升阻力系數和表面壓力特性的影響規律,研究得出以下結論:
(1)數值計算采用k-ω SST湍流模型時,翼型表面法向第一層網格高度應滿足y+小于1的要求;同時,弦向的網格節點越多,升阻力系數的計算結果越接近實驗值。
(2)數值計算時,相比翼型法向的第一層網格高度,翼型弦向的網格節點個數對其表面壓力分布的影響更加敏感。即網格縱橫比影響翼型表面壓力的分布。
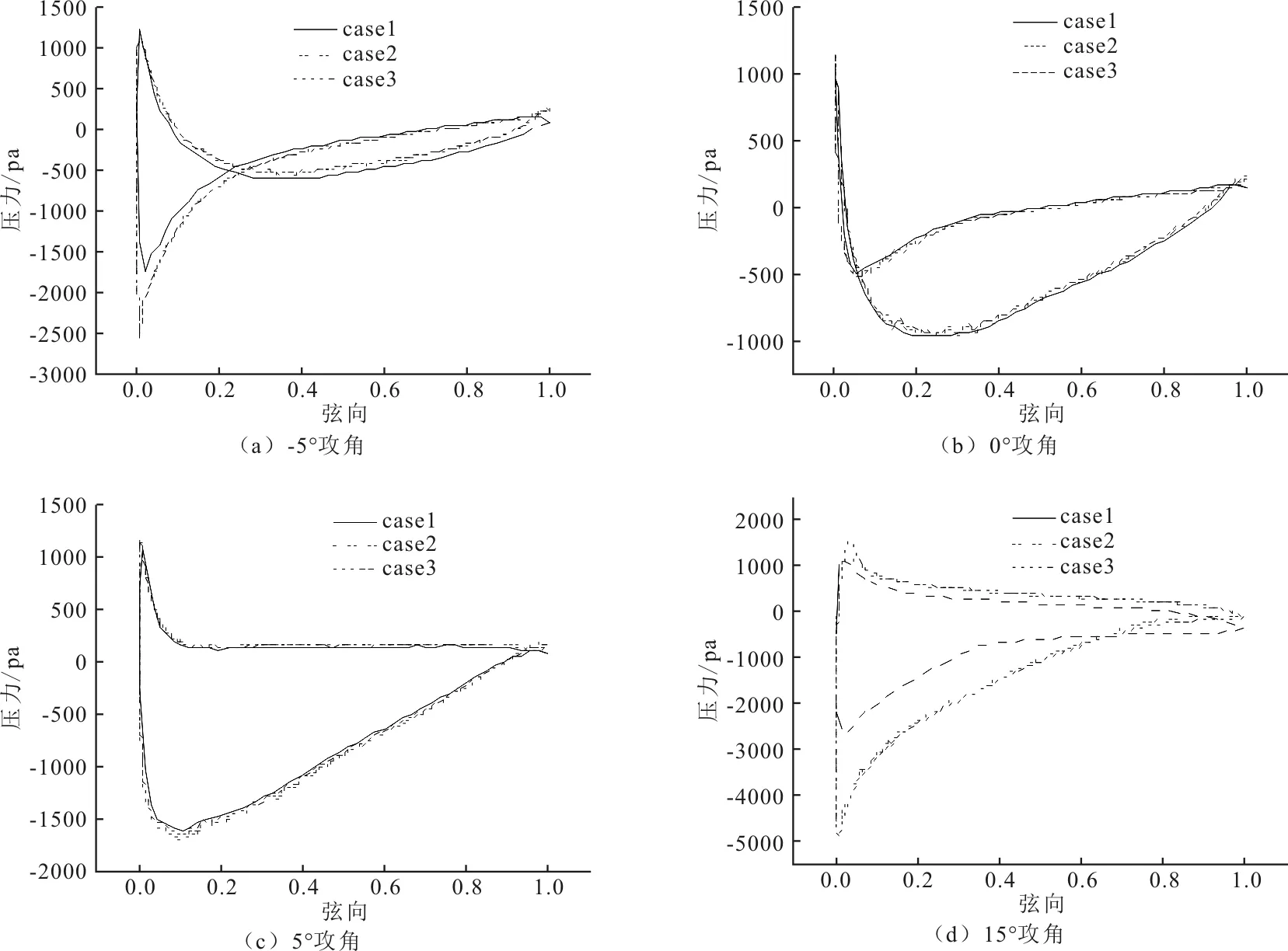
圖7 葉片表面壓力分布

