基于不同機器學習模型的川中丘陵區參考作物蒸散量模擬

黃滟淳，崔寧博,2,3，陳宣全，徐浩若，張藝璇

(1. 四川大學 水力學與山區河流開發保護國家重點實驗室 水利水電學院，成都 610065；2. 南方丘區節水農業研究 四川省重點實驗室，成都 610066；3. 西北農林科技大學旱區農業水土工程教育部重點實驗室，陜西 楊凌 712100)

0 引 言

參考作物蒸散量(ET0)是指高0.12 m、冠層蒸散阻力為70 s/m、反照率為0.23的假想作物的蒸散速率[1]，ET0可以表征某一地區的大氣蒸散能力，是計算作物需水量的基礎，同時也是規劃和設計農田水利工程的重要資料[2]，對作物需水量預測、水資源優化管理具有重大意義。

目前確定ET0的方法有實測法、公式法和數值模擬法，其中實測法操作繁雜，限制條件較多，不易推廣[3]；公式法中的標準模型是由聯合國糧食及農業組織(FAO)于1998年提出的Penman-Monteith (P-M) 模型[1]，該模型較全面地詮釋了蒸散發過程的發生機制，但是P-M模型考慮的因素很多，對于不能獲取完整氣象數據的地區并不適用，因此，基于較少氣象參數輸入的簡化預報模型尤為重要，目前已有60余種簡化模型被相繼提出，包括溫度法中的Hargreaves-Samani模型[4,5]，輻射法中的Priestly-Taylor模型[6]、Irmak-Allen模型[7]，綜合法中的Penman-Van Bavel模型[8]等；數值模擬法將既有氣象數據作為樣本，模型經過學習和訓練，找到非線性關系的最優擬合，該方法高效、可移植性強，在區域范圍廣、氣候條件復雜的地區[3]優勢顯著。

隨著計算機技術及機器模型的發展，越來越多的數值模擬模型被用于ET0的預報。馮禹[9,10]等對中國西南部濕潤地區的ET0預報研究表明，基于溫度和地外輻射數據的隨機森林(RF)和廣義回歸神經網絡(GRNN)模型具有良好的預報效果[9]，極限學習機[10](ELM)的預報效果優于經驗模型。Tabari[11]等將支持向量機(SVM)和自適應神經模糊推理系統(ANFIS)應用于伊朗半干旱區域的ET0預報，預報效果優于經驗模型。Yassin[12]等利用人工神經網絡(ANNs)和基因表達編程(GEP)對干旱條件下的ET0預報進行比較分析，結果表明ANNs模型預報精度高于GEP。

模型樹常被用于數據挖掘和機器學習中，通常采用離散的標簽進行決策分類，相關學者[13,14]對其進行改進，用分段線性函數替代離散分割，為模型樹在連續型數據回歸問題的應用提供了技術支撐。M5回歸樹不同于傳統的神經網絡，其精巧的分段式結構和靈活的模型尺度，使得它拓撲結構直觀、收斂速度快，且能夠得到模擬映射的線性表達，泛化能力更強[15]。目前M5回歸樹已成功應用于降雨—徑流模擬中，在流量及區域降雨的預測問題上表現良好，但還沒有將其利用于ET0預報的相關研究或報道。

本文以P-M模型作為標準，將M5回歸樹(M5-RT)與改進的傳統神經網絡BPNN、GRNN應用于川中丘陵區7個代表性站點的ET0預報，分析不同模型的ET0預報精度和泛化能力，并將其與精度較高的經驗模型進行對比，為川中丘陵區的ET0簡化模擬提供新思路。

1 材料與方法

1.1 基本資料

川中丘陵區位于四川省東部，屬于典型的方山丘陵區，面積約8.4 萬km2，占四川盆地約50%，海拔為250～600 m，地表起伏多但高差變化不大[16]。川中丘陵區是四川省農業生產的重要區域，主要經濟作物有蠶桑、甘蔗、棉花等，區域內氣候災害頻發且持續時間較長[17]，嚴重影響區域內農業發展，實現精準農業管理至關重要。考慮區域內地理、氣候因素，選取7個代表性站點，具體分布見圖1。

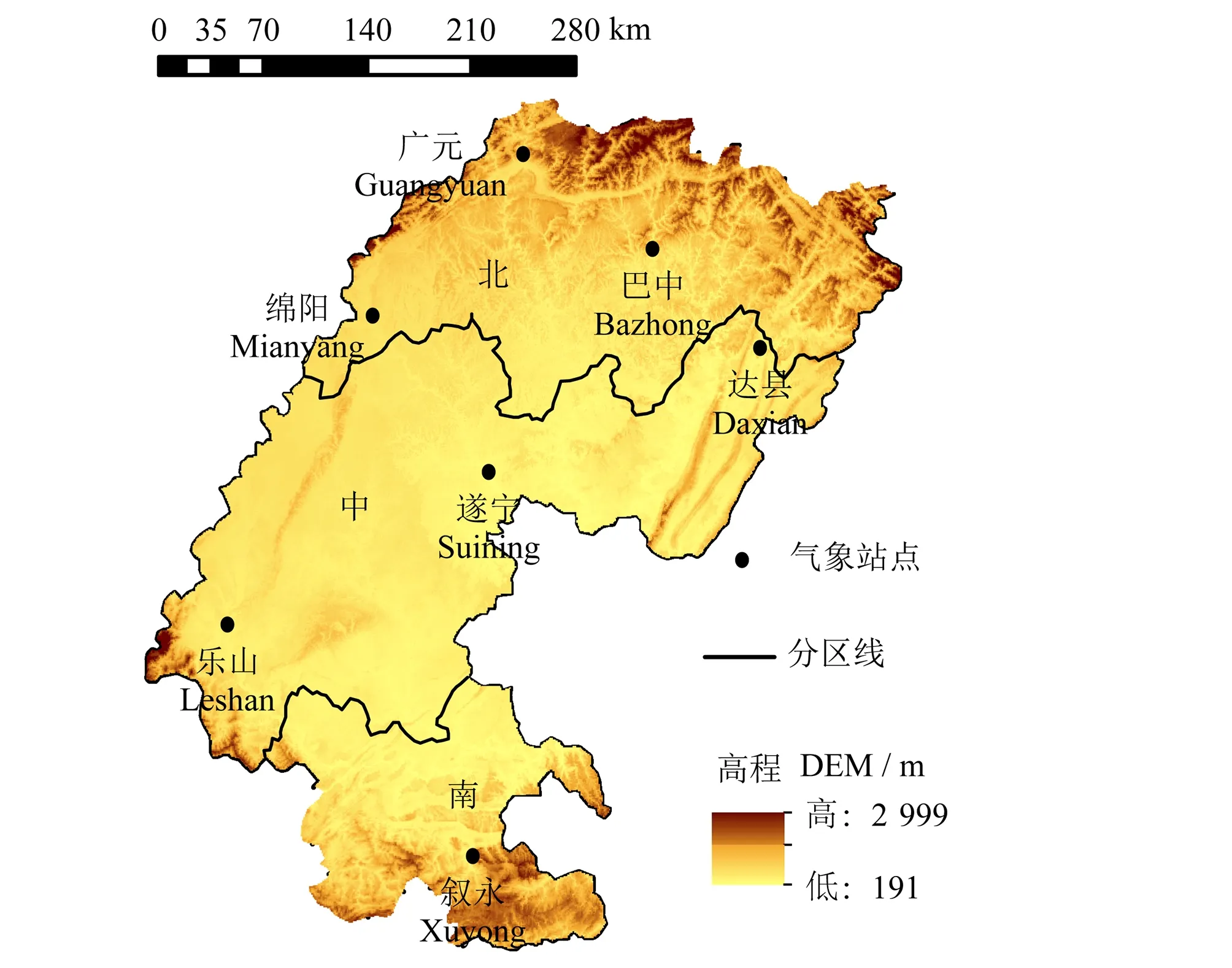
圖1 川中丘陵區氣象站點分布圖Fig.1 Distribution of meteorological stations

1.2 數據獲取及處理

本文所用的川中丘陵區1961-2016年逐日氣象數據均來自國家氣象信息中心(https:∥data.cma.cn/)，包括最高氣溫(Tmax)、最低氣溫(Tmin)、平均氣溫(Tmean)、日照時長(Tsun)、相對濕度RH(relative humidity)、10 m處風速(u10)等。針對達縣、廣元站缺失數據(約占0.15%)，采用線性插值[18]補全。并將1961-2016年的逐日氣象數據按7：3的比例分為兩部分，分別作為訓練集(1961-2000年)和預測集(2001-2016年)。

選取FAO P-M模型[1]的計算值作為ET0標準值，參考P-M模型，風速項的條件為距地面2 m，故由風廓線[1]關系推出式(1)進行轉化。

(1)

式中：z為地面至測點的垂直距離，m；uz為高度z處的風速，m/s。

1.3 ET0計算模型

P-M模型綜合考慮了各種氣象因素，基于水汽擴散理論推導，具有很強的普適性。另外，參考趙璐等[19]對川中丘陵區不同計算方法的比較和改進，以及馮禹等[20]對機器學習模型與Hargreaves模型在四川盆地的對比研究，選取3種在川中丘陵區精度較高的簡化物理模型進行對比，分別是基于溫度、日照時長和大氣頂層輻射的Jensen-Haise模型[21]，李晨等[6]基于貝葉斯原理改進的Hargreaves-Li模型，基于溫度和凈輻射的Irmak-Allen模型[8]，計算公式見表1。

表1 ET0物理計算模型Tab.1 Calculation models of reference crop evapotranspiration

注：Δ為飽和水氣壓—溫度曲線的斜率，kPa/℃；γ為濕度計常數，kPa/℃；Rn為凈輻射，MJ/(m2·d)；Ra為大氣頂層輻射，MJ/(m2·d)；ea為實際水氣壓，kPa；es為飽和水氣壓，kPa；G為土壤熱通量，MJ/(m2·d)；N為白晝時長，h；λ為水的汽化潛熱，取25 ℃下的標準值2.444 MJ/kg參數的具體計算見文獻[1]，特別地，本文獲得的氣象數據以天為周期，可忽略土壤熱通量的影響[1]，故取G=0。

1.4 機器學習算法

1.4.1 M5回歸樹模型M5-RT

模型樹在數據挖掘和機器學習中應用廣泛，其擴展結構如圖2所示，像一棵倒置的樹，葉片代表不同的分類或決策。傳統的模型樹采用離散的標簽進行分類，Wang和Witten[13]對M5回歸樹的葉進行了改進，利用若干個線性函數替代離散標簽，從而實現連續類數據的學習和預測回歸，相關技術由Jekabsons等[14]于2010年繼續完善，并利用Matlab工具箱研發相關程序(http:∥www.cs.rtu.lv/jekabsons/)。

M5回歸樹是一種多元的分段式線性回歸模型，節點選擇時采用貪心算法，理論上可使用足夠多的節點完成任何復雜的非線性回歸，實際建模中為提升收斂速度，會通過后續的剪枝操作[15]對樹模型進行精簡，分段函數的特性，使得M5回歸樹比其他數據模型更為靈活，且能得到映射關系的顯式表達，目前已成功應用于降雨—徑流模擬中。Goyal等[22]將M5回歸樹用于Pichola湖流域降雨量和水量預測，Bhattacharya等[23]將M5回歸樹與神經網絡應用于河流流量預測，取得了優于傳統模型的結果。

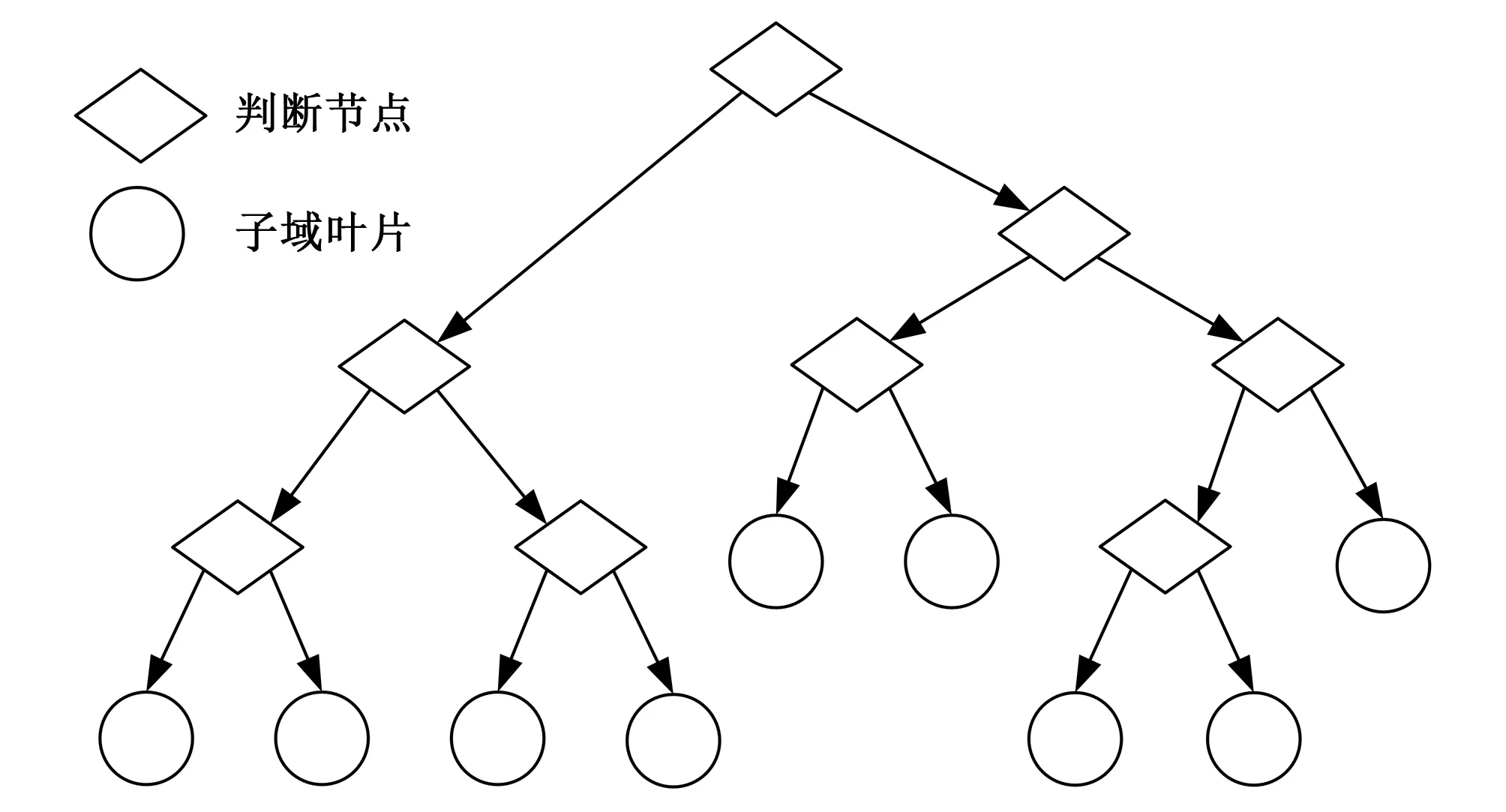
圖2 M5回歸樹結構Fig.2 Structure diagram of M5 regression tree

1.4.2 交叉驗證改良的廣義回歸神經模型CV-GRNN

廣義回歸神經網絡(GRNN)是由Specht[24]提出的一種變形的徑向基神經網絡，以樣本數據為后驗條件，執行Parzen非參數估計[25]，具有很強的非線性映射能力。Ladlani等[26]將GRNN用于阿爾及利亞的ET0預報，并證明其精度優于傳統的徑向基神經網絡。馮禹等[27]將基于溫度資料的GRNN模型用于四川盆地的ET0預報，精度優于物理模型。GRNN模型由4層網絡組成，如圖3，依次為輸入層、模式層、求和層和輸出層。

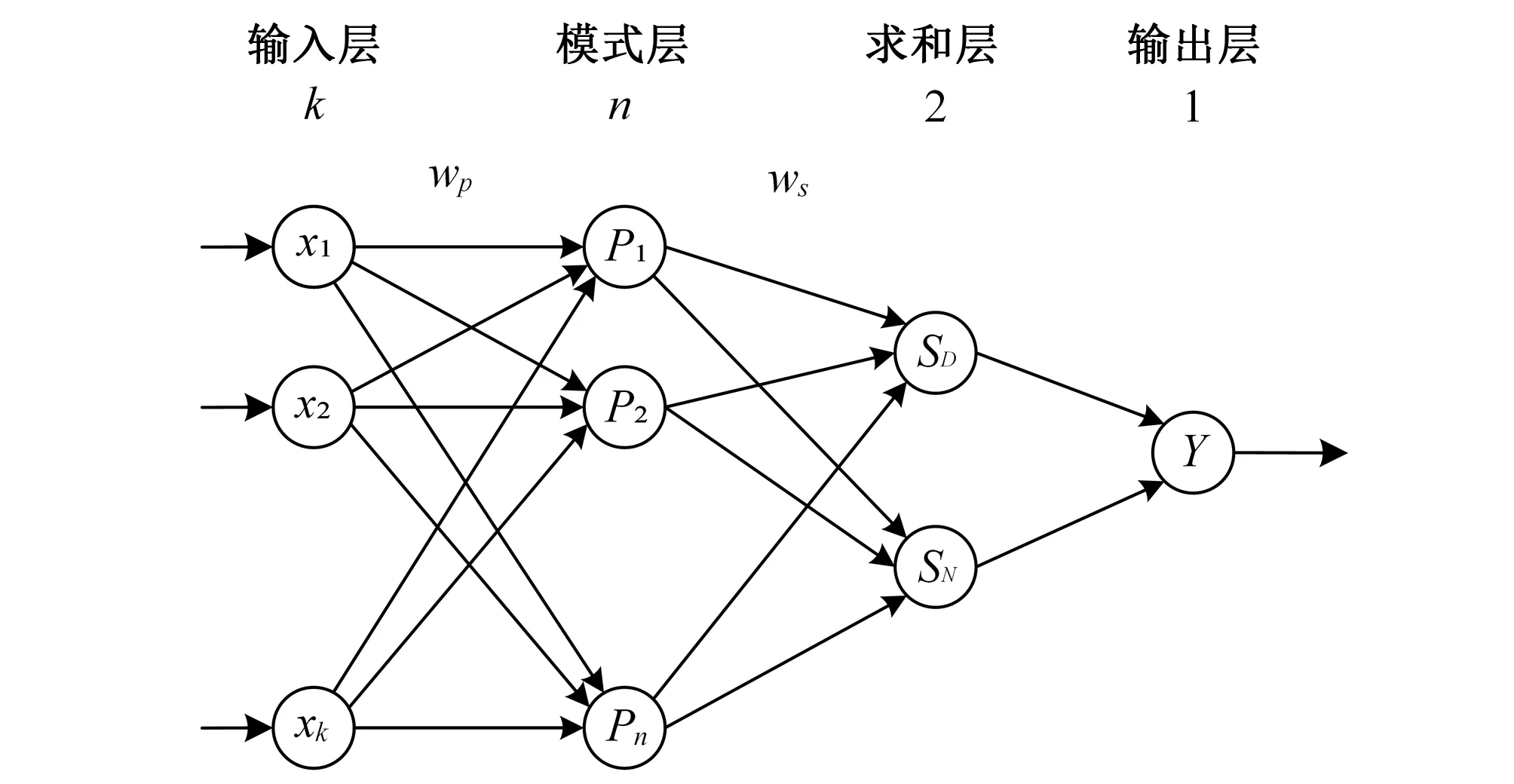
圖3 GRNN模型拓撲結構Fig.3 Topological structure of general regression neural network

(1)輸入層為學習樣本的直接輸入，其神經元個數等于學習樣本中自變量X=[x1,x2,…,xk]的維度k，深度為樣本數量。

(2)模式層與輸入層間通過權重wp連接，模式層的神經元個數等于樣本數量n，各神經元的傳遞函數為，

(2)

式中：Xi為第i個神經元的學習樣本；σ稱為光滑因子，是高斯分布的標準差，其取值影響GRNN網絡的性能，需要優化。

(3)求和層使用兩種計算法則對模式層的神經元進行處理。第一種對模式層所有神經元進行算術求和，連接權值為1，其求和函數如式(3)；第二種對模式層的神經元進行加權求和，本文ET0預報的輸出變量為一維，設樣本輸出值為Y，第i個神經元與第i個輸出變量的連接權值就是Yi，其求和函數如式(4)。

(3)

(4)

(4)輸出層的神經元個數等于輸出樣本的維度，此處為1，模型輸出的估計值是兩類求和層的比值。

(5)

本文選取川中丘陵區7個代表性站點的逐日氣象資料建立GRNN模型，代碼見文獻[28]，同時采用交叉驗證(Cross-validation)算法對光滑因子σ及徑向基擴展速度spread進行優化，將訓練樣本隨機分為5個子樣本，4對1重復驗證5次，在參數的預設范圍內循環求解，確定優化參數建立CV-GRNN模型。

1.4.3 雙隱藏層優化的BPNN模型H-BPNN

1988年，Rumelhart[29]等提出了誤差反向傳播算法，即BP算法，應用于反向傳播神經網絡(BPNN)。BPNN屬于前饋型神經網絡的一種，會根據理想輸出結果和實際預測結果的差值對模型中的傳遞權值進行修正，反復訓練直至誤差達到設定閾值以下或者迭代次數達到最大值[30]。

本文用動量批梯度下降函數(traingdm)替代默認的模型訓練函數trainlm，動量項的引入提高了收斂速度，且能有效避免網絡訓練時[31]陷入局部極小值震蕩。其權重更新規則改進為，

(6)

式中：w(t)為t時刻的權重值；η為學習速率；α為動量因子；E為網絡訓練的誤差。

動量項的添加能加強權重變化方向的記憶效應，使得學習速率加快并有效拜托局部極小值區域。

隱含層的層數和節點個數對模型的預測性能和泛化能力有很大影響[32]，過擬合或欠擬合都會產生較大誤差，因此，需要預試驗確定模型的最佳結構[33]。本文采用雙隱含層的BPNN網絡，節點數取值范圍初設為1～20，基于廣元站的氣象數據進行優化求解，代碼基于Matlab 2018a，具體見文獻[28]，以均方根誤差為考察目標，設置最大迭代次數為4000，求解最優隱含層節點數，預試驗結果見圖4。

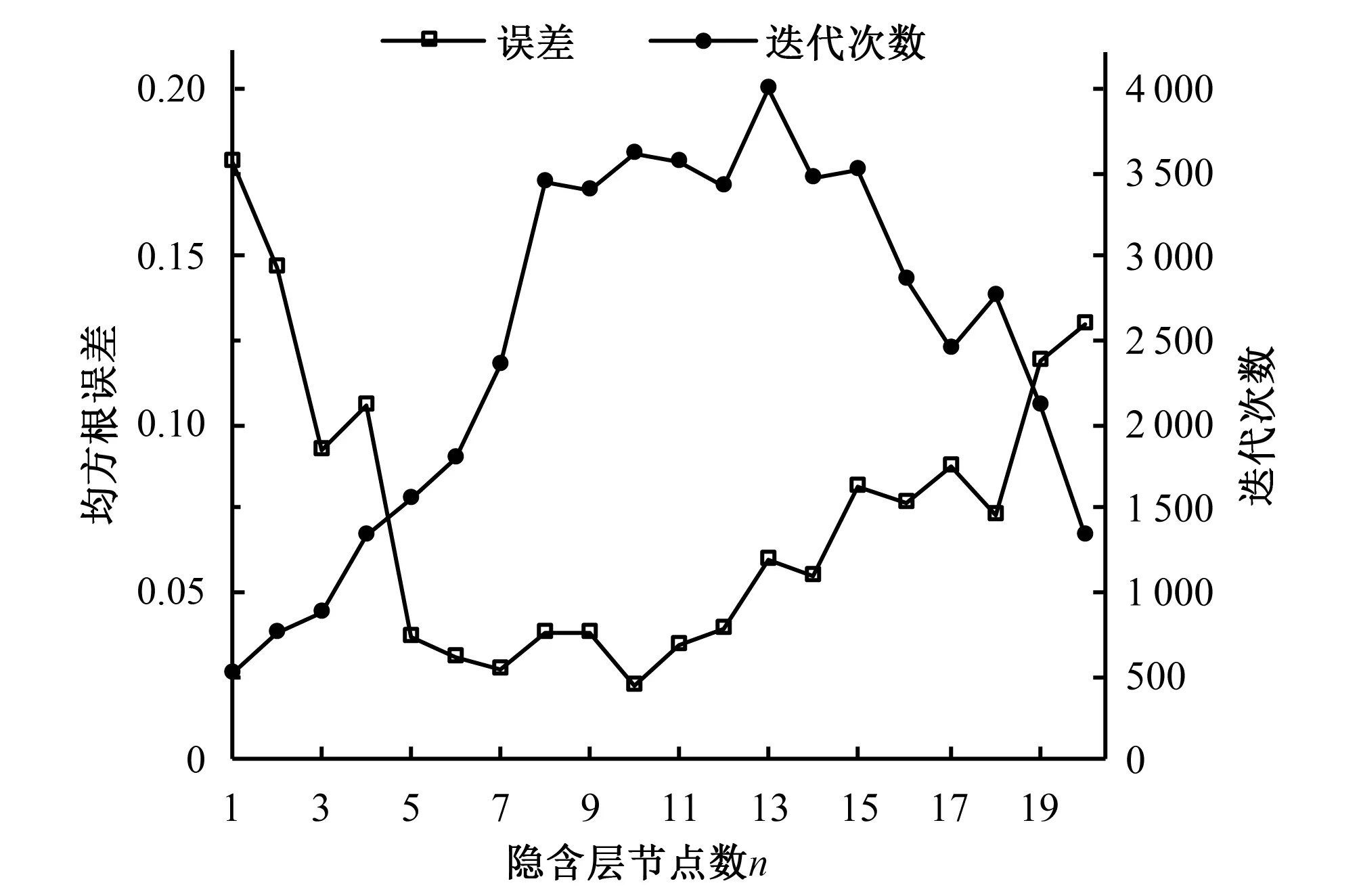
圖4 BPNN網絡性能與隱含層節點數的關系Fig.4 Performance of back propagation neural network in different hidden neurons

由圖4，模型誤差與隱含層節點數量n大致呈拋物線關系[34]，綜合考察迭代次數及網絡精度，本文建立隱含層節點數為7的雙隱含層H-BPNN模型，模型結構見圖5。

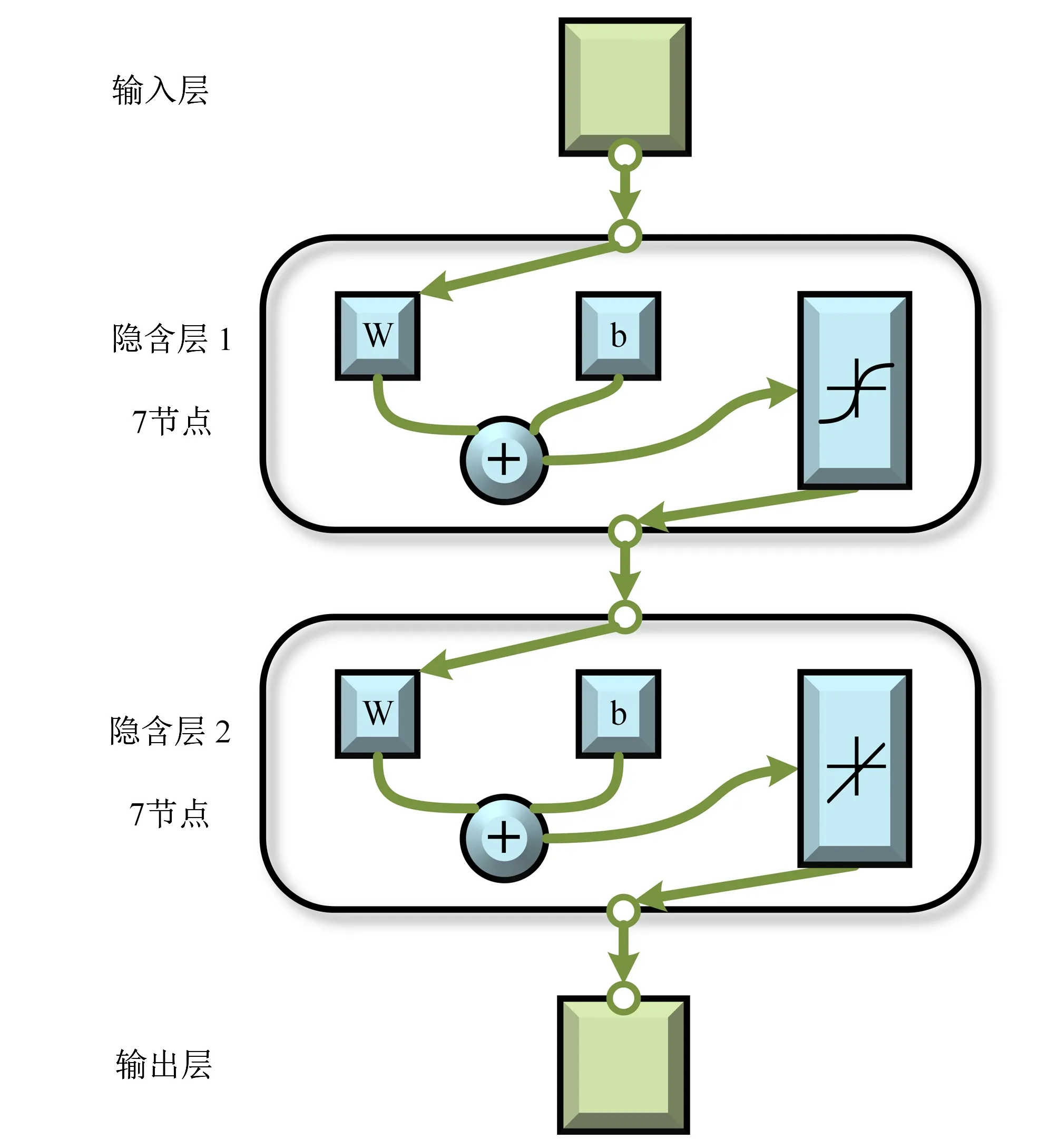
圖5 H-BPNN模型結構圖Fig.5 Structure diagram of H-BPNN

1.5 模型輸入層

劉昌明等[35]對全國主要流域的地表潛在蒸散量敏感性研究表明，風速與日照時數的下降是造成ET0減小的主要原因。另一方面，太陽輻射是引起白晝溫差的主要原因，Hargreaves[36]和Samani等[37]利用溫差和大氣頂層輻射(Extraterrestrial Radiation，Ra)對地表凈輻射進行推演，彌補Tsun的缺失。因此，本文在輸入項的氣象因子組合中優先考慮溫度和u2，并比較Tsun和Ra的作用，建立如表2的4種輸入組合。

式(7)中Ra是與站點緯度(Latitude，單位rad)和日序數(J，每年1月1日起從1開始循環)相關的函數，具體計算方法見文獻[1]。

Ra=F(Latitude,J)

(7)

1.6 模型評價因子

本文根據模型預測結果和P-M模型計算結果計算4個統計參數對模型預報精度進行評價，分別是納什效率系數NSE，均方根誤差RMSE，平均相對誤差MRE和決定系數R2，并由對應的綜合指標GPI[38](global performance indicator)對模型性能進行排序。MRE和RMSE越接近0，R2和NSE越接近1，表明模型預報精度越高，故GPI計算公式如式(8)，GPI越大，模型精度越高。

表2 模型輸入項參數組合Tab.2 Input combinations and parameters

注：InputI(I=1, 2, 3, 4 )表示4種不同的輸入組合，下同；按輸入項維度遞減排列，其中大氣頂層輻射Ra可由日序數和緯度直接計算[1]，非觀測量。

(8)

式中：Ckm為模型m的第k個參數；Midk為所有模型中參數k的中位數；GPIm為模型m的綜合得分。

對于R2和NSE，ηk=1，對于MRE和RMSE，ηk=-1。

2 結果分析

2.1 各模型ET0日值預報結果及精度分析

根據1.6的模型評價方法對各模型的ET0預報結果進行分析，計算川中丘陵區不同模型ET0預報的統計參數，7個站點的參數范圍見表3。由表3可知，輸入組合為Input 1(Ra、Tmax、Tmin、RH、Tsun和u2)時，M5回歸樹(M5-RT)表現出極高的精度，NSE、RMSE、MRE和R2的變化范圍分別為0.998 0～0.999 2、0.037 4～0.058 0 mm/d、0.88%～1.62% 和0.998 2～0.999 2，GPI排名第1，CV-GRNN和H-BPNN模型也有較好的預報精度，其NSE和R2均大于0.940 2。在3種數值模擬模型中，M5-RT最優，H-BPNN次之，CV-GRNN相對較差，但3種模型的NSE均大于0.843 8、R2均大于0.893 3、RMSE均小于0.5 mm/d、MRE均小于13.59%，都能在一定程度上呈現氣象參數與ET0間復雜非線性映射關系，且模擬精度均高于所選經驗模型，尤其是M5回歸樹，在4種輸入項組合下都有最優的表現，從圖6可以看出M5-RT模擬預報誤差的異常波動最小，在川中丘陵區的ET0預報研究中有很高的實用價值。

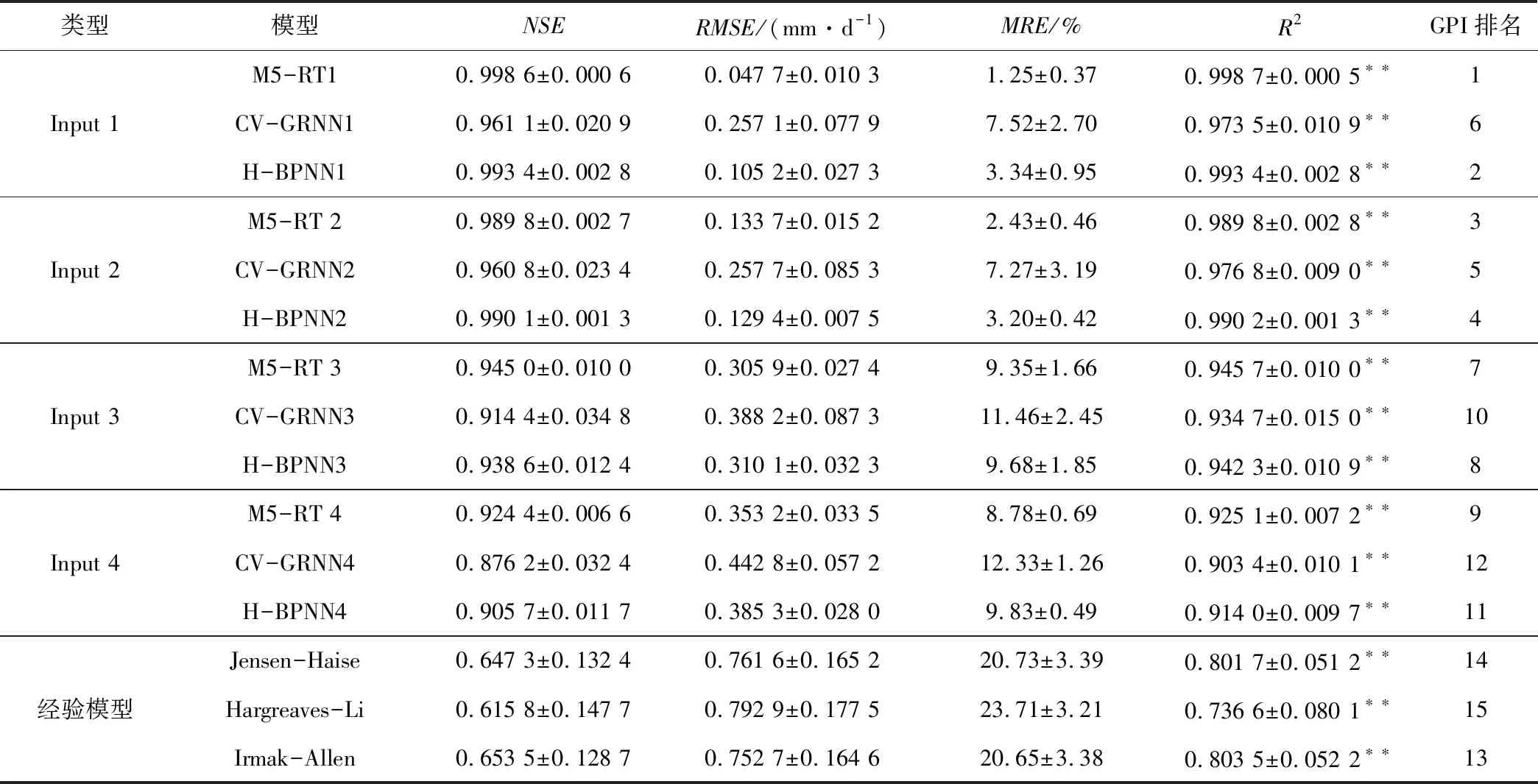
表3 川中丘陵區不同模型的逐日ET0預報精度Tab.3 Daily statistic performance evaluation results for different models in hilly area of central Sichuan

注：XXXI(I=1, 2, 3, 4 )分別表示4種不同輸入下的XXX模型，下同；**表示在1%的水平上顯著相關；“x±y”表示參數范圍是[x-y,x+y],下同。

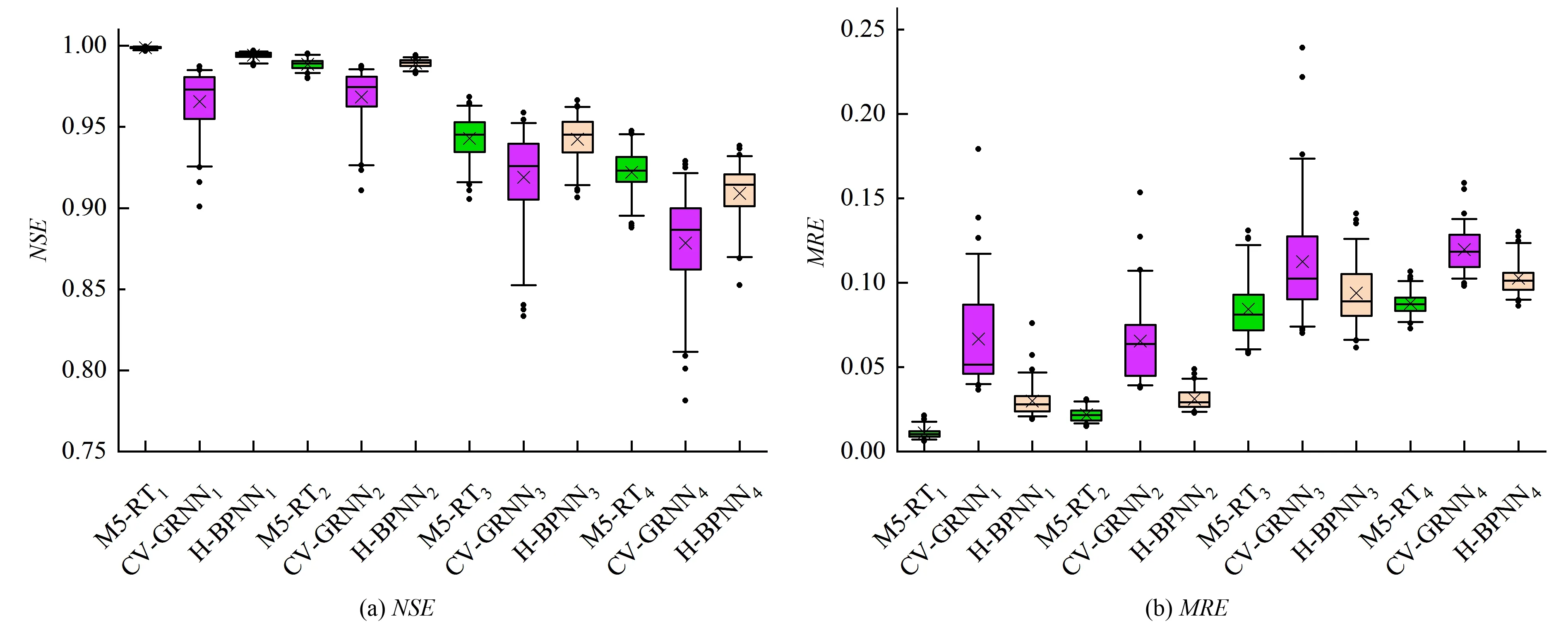
圖6 2001-2016年川中丘陵區不同模型ET0日值預報誤差箱線圖Fig.6 Box-plot of ET0 forecasting accuracy for different models in hilly area of central Sichuan from 2001 to 2016

Input 1包含了最多的氣象因子，從圖6的整體變化趨勢不難發現，Input 1下模型具有精度最高，其他3種輸入組合下模型的精度隨輸入參數減少而降低，但M5-RT、CV-GRNN和H-BPNN的ET0預報精度仍處于較高水平。在缺省氣象資料的情況下，模型的可靠性以及實用性評價需要考量減少輸入項對模型精度產生影響的程度，只要總體精度達標，相比全輸入模式下輕微的精度降低是可以被接受的，這一點在Input 2和Input 3上表現極為突出。

Input 2相比于Input 1去掉了Tsun和RH，模型預報精度降低幅度低于0.4%，CV-GRNN模型反而略有升高，其精度波動可以歸于模型訓練的隨機性誤差，即Tsun和RH的缺失對數值模擬模型幾乎沒有影響。正如Hargreaves[36]和Samani[37]等研究發現，利用溫差和Ra對地表凈輻射進行推演，能彌補Tsun在模型中的作用，劉昌明[36]等的研究也表明風速對ET0的影響力遠大于RH。另一方面，Input 3在Input 2的基礎上(去掉了Ra)約有5%的精度降低，進一步體現了大氣頂層輻射Ra的重要性。

Input 4(Ra和u2)輸入下，M5和H-BPNN均表現出良好的預報精度，NSE和R2均大于0.9、RMSE均小于0.4 mm/d、MRE均小于10%，模型精度高于其他在川中丘陵區適應能力較好的物理模型。Input 4保留了最為重要的氣象因子，其中Ra是溫差與輻射的體現，風速與其他氣象參數(例如溫度和輻射)的關系比較微弱，這種不可替代性使得對模型性能有著重要的影響，這一點與張皓杰[39]和馮禹[20]的研究結論一致，在地理環境、氣候條件各異的不同流域內，風速對地表蒸散發的影響均不可忽視[35]。

2.2 M5-RT、CV-GRNN、H-BPNN模型可移植性分析

Input 2(Ra、Tmin、Tsun和u2)在較少輸入的情況下取得了較高的ET0預報精度，輸入項中的Ra使得模型學習到更多關于站點地理位置的信息。本文為檢驗模型在川中丘陵區不同地區間的適應能力，在Input 2的基礎上，將7個代表性站點按照緯度分為3類(偏北部的廣元、綿陽、巴中，偏中部的樂山、達縣、遂寧，偏南部的敘永)，以敘永站2001-2016年逐日氣象資料及P-M模型計算的ET0作為輸出，分別從北、中各3個站點中隨機抽取20年日值數據進行組合，即建立“北-南”、“中-南”兩類訓練-預測組合，訓練集數據量為60年，預測集數據量為16年，按照1.6節的模型評價方法計算相關參數，并將預報結果與P-M模型標準值進行比較，圖7為P-M模型計算結果與模型預測輸出的散點圖。

可移植性分析結果表明，訓練、預測站點交叉組合下，3種模型的預報精度都較高，NSE和R2均大于0.9。同時，其精度與相同輸入下的獨立站點模擬精度相比都有一定程度的降低，特別是均方根誤差RMSE，增大了近50%～100%。

由圖7可知，M5-RT模型兩種站點交叉組合下模型的ET0預報能力接近，R2為0.955 7～0.956 0，NSE為0.953 3～0.955 2，模擬結果平均相對誤差約為7.5%～7.6%，精度降低約5%，RMSE為0.29～0. 31 mm/d，ET0模擬輸出較為穩定，精度波動較小，整體效果好；H-BPNN模型和CV-GRNN模型出現明顯的截斷誤差，當ET0大于6 mm/d時，預報值普遍過小，具有一定局限性，模型可靠性降低；CV-GRNN模型在整體上相關性較好，但預測值與標準值的趨勢線斜率較小(0.819和0.913)，ET0預報值較低，效果相對較差。對比發現M5-RT模型泛化能力最強，在氣候條件接近的地區間預報能力優且穩定，可作為川中丘陵區預報ET0的理想模型。

3 結 論

(1)日尺度誤差分析表明，4類輸入項組合下，M5回歸樹模型最優，H-BPNN模型次之，CV-GRNN模型相對較差，且對比不同輸入組合下模型精度發現，Tsun和RH對ET0預報的影響很小，而Ra和u2對模型的精度影響較大。另外，3類機器學習模型的ET0預報精度都較高， 其中R2為0.89～0.99，NSE為0.84～0.99，MRE為1.25%～12.45%，RMSE為0.05～0.49 mm/d，優于經驗模型Jensen-Haise、Hargreaves-Li和Irmak-Allen。

(2)當輸入項氣象因子減少時，3類機器學習模型的預報精度均有一定程度的降低，但M5-RT模型表現最優，特別是氣象因子數量最少的Input 4輸入下，M5-RT仍表現出良好的預報效果，其R2為0.917 9～0.932 3，NSE為0.917 8～0.931 0，RMSE小于0.386 7 mm/d，MRE小于9.48%，在川中丘陵區的適應性最廣。M5-RT3和M5-RT4均可作為氣象數據缺失下川中丘陵區ET0預報的推薦模型。

(3)通過Input 2下各模型的可移植性分析發現，M5回歸樹泛化能力最強，預報能力優且穩定。整體上，ET0大于6 mm/d時，H-BPNN模型和CV-GRNN模型出現明顯的截斷誤差，且CV-GRNN模型的ET0預報值普遍偏小， M5回歸樹更適合作為川中丘陵區預報ET0的推薦模型。M5回歸樹良好的泛化能力使得當某地區氣象數據在時間尺度上殘缺時，可以適當采用附近地區的氣象數據用于M5回歸樹的訓練，仍可獲得精度較高的ET0預報結果。

M5-RT、CV-GRNN和H-BPNN等數值模擬模型能辨析出氣象因子間固有的隱含關系，完成部分氣象因子的替代和剔除，從而減少觀測層面的工作量，這正是一般經驗模型所不具備的能力。為進一步分析各個氣象因子對ET0預報精度的影響，應設置更多的輸入組合進行對比分析。

□