基于灰色系統理論的水庫移民安置進度偏差預測分析
李貴博,姚凱文,張 丹 ,李寧寧
(1.廣東省水利電力勘測設計研究院,廣州 510000;2.華北電力大學可再生能源學院,北京 102206)
0 引 言
水庫移民安置工作在整個水利工程中無論從投資還是工作量上都占有很大的比重,水庫移民安置工作的順利進行,對維護當地社會穩定,保證水利樞紐工程順利完工有著積極的意義。為保證工程的按時完工,移民安置部門會提前制定進度計劃,但由于水庫移民安置工作的復雜性,在實際實施過程中,意外情況時有發生,從而導致安置工程的實際進度偏離預定的計劃,嚴重影響了整個水利工程的按時完工,對經濟、社會的發展均有著較大的影響。因此,移民安置部門需要及時掌握工程進度信息,找出進度偏差產生原因,從而采取有效措施進行進度控制,保證移民安置任務按時完工[1]。
同其他的施工類自然工程不同,水庫移民安置工作涉及數以萬計的移民征地搬遷等問題,在實施過程中變數更大,工作開展更加困難,具有明顯的動態特征和不確定性,同時有具有信息不完備、數據少的特征。
灰色系統理論與1982年被鄧聚龍教授提出,該理論主要適用于將“部分信息已知,部分信息未知” 的“小樣本、貧信息”的不確定性系統作為研究對象,通過提取部分已知信息中有價值的內容,實現對系統運行行為、演化規律的正確描述和有效監控。目前,灰色系統中的GM(1,1)預測模型被廣泛運用到各類工程的進度偏差分析中,并取得了不錯的效果,移民安置工程符合該系統的特點,因此本文嘗試采用GM(1,1)建模,探究其在移民安置工程進度偏差分析上的應用[2]。
1 灰色預測模型
灰色系統預測是通過建立灰色模型對原始數據進行累加,發現、掌握原始數據的規律,得出規律性較強的曲線,進而對整個系統做出科學合理的定量預測[3]。目前運用最普遍的灰色預測模型就是GM(1,1)預測模型,其建模過程如下。
1.1 GM(1,1)模型的建立[4]
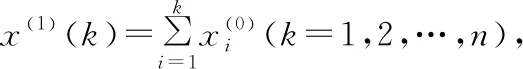
GM(1,1)預測模型的微分方程為:
(1)
式中:a、b均為常數,a稱為發展系數,b稱為內生控制灰數。
通過最小二乘法擬合可以得到 與 的值。具體計算公式為:
[a,b]T=(BTB)-1BTYN
(2)
其中:
(3)
YN=[x(0)(2),x(0)(3),…,x(0)(n)]T
(4)
最終求出發展系數的大小不同,其模型可進行預測的效果也不同,具體關系如表1。

表1 發展系數取值與預測效果關系表[5]Tab.1 The relation table of the value of development coefficient and the effect of prediction
預測模型微分方程的解為:
(5)
(k=1,2,…,n)
上式為累加數列的預測值公式,若想預測原始數列,可通過對上式進行累減計算得到公式:x(0)∧(k+1)=x(1)(k+1)-x(1)(k)。
1.2 模型精度檢驗[6]
得到預測值后,要經過檢驗后才能判定該模型是否合理。目前最為常見的精度檢驗方法有殘差檢驗和后驗差檢驗,下面將兩種檢驗方法的步驟作簡要介紹。
(1)殘差檢驗。殘差檢驗的具體步驟為:
①計算原始數列與對應模型計算值的殘差:
δ(0)(k)=x(0)(k)-x(0)∧(k)
(6)
②計算原始數列與對應模型計算值的相對誤差:
(7)
一般認為,當M(0)(k)<0.2時,模型的殘差檢驗為合格。
(2)后驗差檢驗。后驗差檢驗的具體步驟為:
(8)
(9)
②計算均方差比c與小誤差概率p,計算公式如下:
(10)
(11)
模型精度由c與p的值共同決定,具體關系如表2所示。

表2 后驗差檢驗精度等級參照表Tab.2 Precision grade reference table of inspected by posterior difference check
2 實例應用
本文采用國內某水庫移民工程作為計算實例,以移民搬遷人數來反映移民安置工作的進展情況,對其從2014年12月到2017年6月期間的六次移民搬遷人數統計數據進行偏差預測分析,在殘差檢驗合格后,利用已知的2017年12月的數據對模型進行二次檢驗,確保模型在移民安置偏差預測中的可行性。
2.1 模型建立
該工程在移民安置工作初期,首先進行了移民安置試點,試點范圍內207戶800人的移民安置規劃設計已由項目法人單獨委托完成,該試點的800人不用于本次建模計算,該工程移民的全面搬遷工作于2014年開始進行。據統計,從2014年6月到2017年6月,各時間截點的累計移民搬遷人數如表3所示。
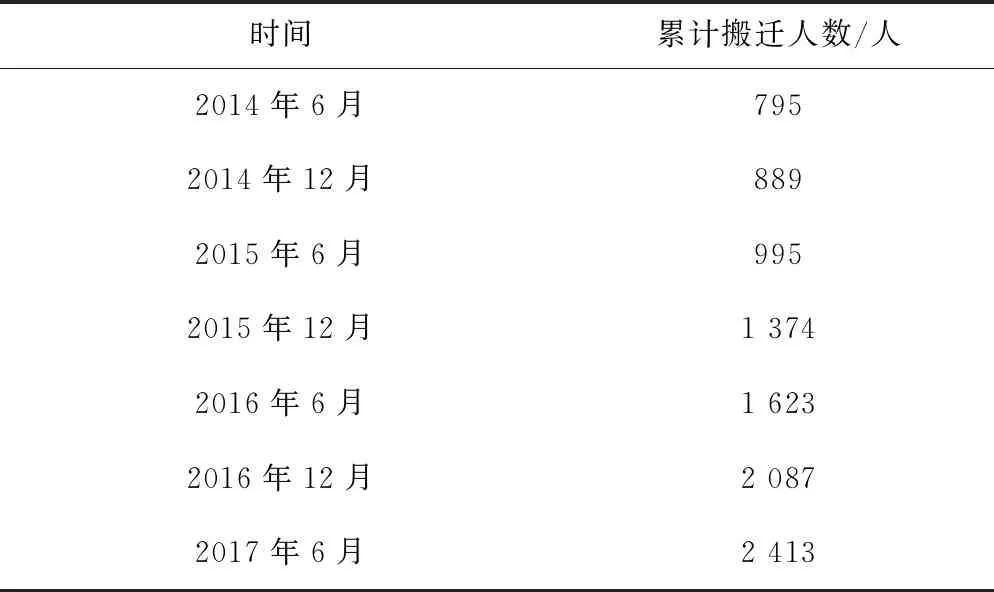
表3 工程各時間截點累計移民搬遷人數統計表Tab.3 Cumulative number of migrants at different time points in engineering
該數據為累計人數,以2014年6月的搬遷人數作為基準點,通過計算可得到原始序列,即:X(0)=(94,106,379,249,464,326)。
通過將原始數據累加計算得到累加序列:X(1)=(94,200,579,828,1292,1618)。
將求出的兩個常數帶入式(5)即可得到該工程移民搬遷人數的偏差預測模型,需要注意的是:由于計算以2014年6月的搬遷人數作為基準點,故在式(5)中應加入2014年6月的搬遷人數。通過計算可得:
1 430.613 7 e0.146 0 k-541.613 7
(12)
2.2 模型檢驗
選取不同的k值,帶入偏差預測模型計算得出各時間截點移民搬遷人數的預測值,并進行殘差檢驗及后驗差檢驗,由表4中的結果可知,殘差檢驗結果中,模型的相對誤差均小于0.12,滿足精度的要求,檢驗結果為合格;后驗差檢驗結果中,均方差比為0.472,小概率誤差為0.833,即0.3 現已知2017年12月累計移民搬遷人數為2 839人,現令k=6,計算2017年12月的移民搬遷人數預測值為2 894 人,相對誤差僅為0.019 4,結果表明該模型在水庫移民安置進度偏差預測上精度較高。另外,由于-a=0.146≤0.3,因此該模型可用于中長期預測,這也迎合了水庫移民安置工作時間跨度較長的特點。 表4 工程移民搬遷人數預測模型殘差檢驗計算表Tab.4 Residual test of migration number prediction model of the engineering 將除去試點搬遷800 人后的規劃搬遷總人數8 812 人帶入模型,求得K值為12.86,即全部移民搬遷工作完成時間預測結果為2021年5月。根據移民安置規劃,該工程移民全部安置完畢的規劃時間為2020年,即預測結果表明該工程的進度已經嚴重滯后。因此,移民安置部門要采取有效措施,加快移民安置進度,根據筆者多次實地走訪調查該工程的經驗,針對工程的實際情況,現提出幾點加快移民安置進度的建議如下: (1)進一步提高認識,明確責任,加強對水庫移民工作的組織領導。各有關鎮(辦)要切實落實鎮政府是水庫移民安置工作的“責任主體、工作主體、實施主體”三個主體責任,要進一步統一思想、提高認識,加強領導、落實責任,嚴格按照縣委、縣政府的部署要求,實行各級“一把手”負總責、分管領導具體負責的工作機制,相關鎮(辦)要進一步調整優化移民工作機構,至少確定2名責任心強、對農村工作熟悉的業務骨干具體開展此項工作。 (2)做好水庫移民政策宣傳。針對庫區移民對移民搬遷政策掌握不準,理解不清等問題,各鎮(辦)要加大移民政策宣傳培訓力度,通過入戶宣講、發放宣傳冊、開村民大會等多種形式認真宣傳水庫移民搬遷安置有關政策,使移民政策在庫區進村入戶,做到家喻戶曉,消除移民群眾政策上的疑慮,解除搬遷顧慮。 (3)及時、高效地簽訂移民搬遷安置協議。各鎮(辦)要依據相關文件,對移民戶數、人口和實物指標進行搬遷前的最后核定,依據核定的移民人口和實施補償補助項目內容,及時與接安地鎮(辦)對接,組織與移民戶簽訂搬遷安置協議,協議中應明確安置地點、搬遷時間、建房方式等有關內容,必要時,各鎮(辦)組織對搬遷安置協議進行公證,對符 合安置政策的移民做好資金兌付工作。 (4)切實做好已搬遷安置移民的后續工作。為確保移民“搬得出,穩得住,能逐步致富”,各鎮(辦)要對已搬遷安置的移民及時接轉戶口等關系,拆除庫區房屋附著物,做好已安置移民的生產生活保障。 根據模型檢驗的結果,證明了GM(1,1)模型在水庫移民安置進度偏差預測上的可行性,灰色系統理論為移民安置機構在工程進度控制上提供了一定依據,使其可隨時掌握工程進展的快慢,是否能夠按計劃完工,從而及時采取有效措施進行進度調整。通過模型計算,得到實例工程移民搬遷安置工作的完工時間將滯后一年以上,移民安置部門應從加強組織領導、做好政策宣傳、及時簽訂協議、完善后續工作等方面來加快移民安置進度。 □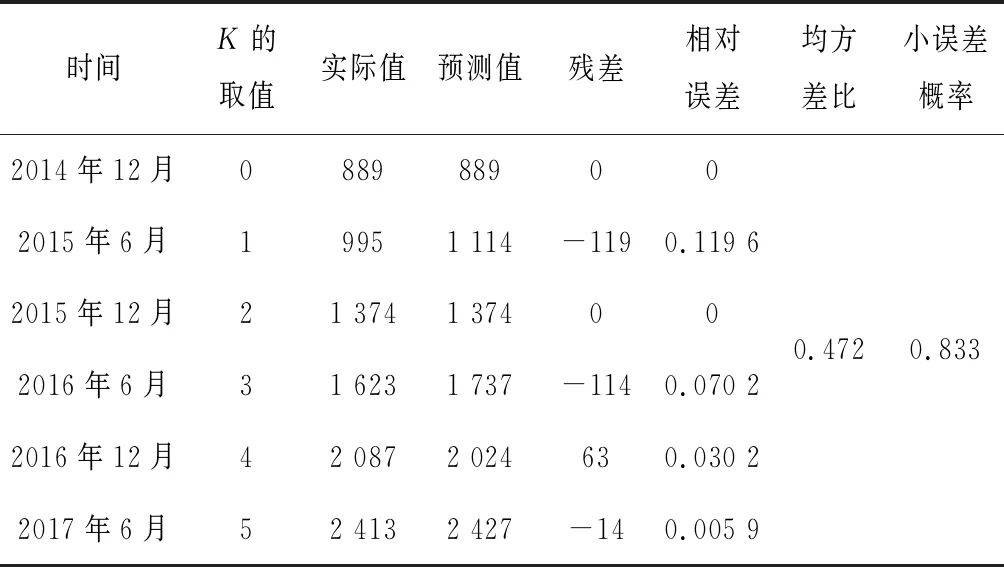
2.3 工期偏差預測分析
3 結 語

