基于光場成像技術的散射性火焰溫度場重建

黃興，齊宏，*，牛志田，任亞濤，阮立明

（1.哈爾濱工業大學 能源科學與工程學院，哈爾濱150001； 2.空天熱物理工業和信息化部重點實驗室，哈爾濱150001）

高溫燃燒廣泛存在于航空航天、能源動力、鋼鐵冶金、化工等領域，發動機、燃氣輪機、內燃機等高溫設備中均存在燃燒現象。火焰作為燃料燃燒時生成的劇烈的光熱現象，其溫度場直接表征了燃燒的狀態，如燃燒的穩定性、燃燒效率、反應速度、火焰三維結構等。準確測量燃燒過程中火焰的溫度分布，不僅可以更好地認識燃燒產物的生成機理與火焰中的熱量傳遞和吸收過程，還可以為生產設備的安全運行、燃料熱能的充分利用及燃燒污染物的有效控制提供數據支撐。如在航空發動機的設計中，燃燒室出口溫度是一項很重要的設計參數，可作為衡量發動機性能的一項重要指標，對其溫度進行測量可為發動機設計提供參考。因此，對火焰空間測溫技術的研究有十分顯著的現實意義。

目前，常用的測溫手段主要分為接觸式測量和非接觸式測量2類。對于接觸式測量，測溫元件需要接觸火焰，這會導致火焰流場受到干擾，且接觸式測量為點測量方式，無法實現整個溫度場的測量。近年來，基于輻射成像的火焰測溫技術受到了國內外學者的廣泛關注［1-3］。該方法具有非侵入式、無需外加激勵源等優點，而且可以通過圖像記錄整個火焰輻射場的信息，進而實現場參數的重建［4-7］。根據成像元件的數量，輻射成像測溫法可以分為單相機和多相機2類。單相機系統結構簡單、易于實現，但由于成像角度受限，難以實現復雜形狀火焰溫度場的測量；多相機系統是在火焰周圍不同位置和角度布置多個相機進行同時成像，以獲得多個角度的輻射圖像［8-10］，該系統空間分辨率高，但是系統復雜成本高，而且操作更為繁瑣。2005年，斯坦福大學的華裔學者Ng等［11］將光場成像的理論和技術應用于商業化，也為火焰輻射成像測溫法提供了新思路。光場相機內部特有的微透鏡陣列結構，可以通過單相機一次曝光記錄全場的輻射光場信息，包括輻射強度的大小、位置及角度。該技術具有高的時間和空間分辨率，可以解決單相機采樣角度有限及多相機系統復雜操作困難等一系列問題，因此基于光場成像技術的高溫火焰溫度場測量技術是一種非常有應用前景的測溫手段［12-14］。

基于輻射成像的高溫發光火焰溫度場重構問題，從本質上是根據邊界輻射強度分布求解輻射傳輸體系中溫度場的問題，這是一個典型的輻射反問題。許多學者開展了有關重構模型與方法的研究。2002年，周懷春等［4］利用改進的Tikhonov正則化方法在CCD相機獲取的火焰圖像中重建出三維溫度場，并證明了改進的Tikhonov正則化方法具有強的抗測量誤差能力。2009年，黃群星等［5］采用立體適配器在一個高分辨率相機成像面上獲得不同探測角度的火焰圖像，充分利用了相機的分辨率，采用最小二乘QR（LSQR）分解算法和雙色法實現了非穩態火焰斷面二維溫度和煙黑顆粒體積分數同時重建計算，得出了火焰斷面的重建結果。2010年，劉冬和岑可法等［15］采用LSQR算法結合反向蒙特卡羅法實現二維、三維爐內溫度場的反演，基于該方法，進一步采用8臺CCD相機對300MW 煤粉爐爐膛的火焰溫度分布進行了重建，獲得了不同高度截面上溫度分布規律［16］。2012年，劉冬等［17］在LSQR算法與截斷奇異值分解算法（TSVD）的基礎上，結合遺傳算法（Genetic Algorithm，GA）構造了2種混合優化算法，利用GA的隨機搜索能力減弱非最優正則化參數對于重建精度的影響。2014年，婁春等［18］利用Tikhonov正則化和廣義截斷奇異值分解的混合算法（TR-GSVD）重建了爐內的三維溫度分布，并指出在重建過程中需要更新正則化參數。2016年，周懷春等［10］利用修正的Tikhonov正則化方法重建出了超臨界鍋爐爐膛內部的溫度分布。目前，雖然大量學者針對輻射成像溫度場重構問題開展了工作，但仍少有關于基于光場成像的火焰溫度場重建反問題的報道。本文主要在光場成像及火焰輻射傳輸模型的基礎上，開展吸收散射性火焰溫度場重建算法研究，將Landweber算法應用到基于光場成像的火焰溫度場重建，以具有較高計算精度的廣義源項多流法作為正問題模型，采用Landweber算法作為反問題求解算法，根據光場成像模型模擬獲得吸收散射性介質的輻射強度光場圖像，據此重構出其三維溫度分布。同時將在輻射成像測溫中廣泛應用的LSQR算法引入到本文研究中，作為對比以檢驗Landweber算法的性能。

1 光場成像及火焰輻射傳輸模型

1.1 光場成像模型

對于基于光場成像的高溫火焰溫度場重建問題，首要問題是建立準確可靠的成像模型以從拍攝得到的光場圖像中提取全場的輻射強度分布。光場相機的內部結構如圖1所示。與傳統相機不同，在光場相機中，主透鏡和傳感器之間加裝了微透鏡陣列。火焰上一點發出的若干采樣光線在經過主透鏡之后匯聚于主透鏡像面上的一點，再被微透鏡陣列分散成若干束投射到不同的傳感器像素上。每個像素上的采樣光線方向信息可由像素和與之對應的微透鏡確定，而其強度信息可通過圖像的灰度值確定。

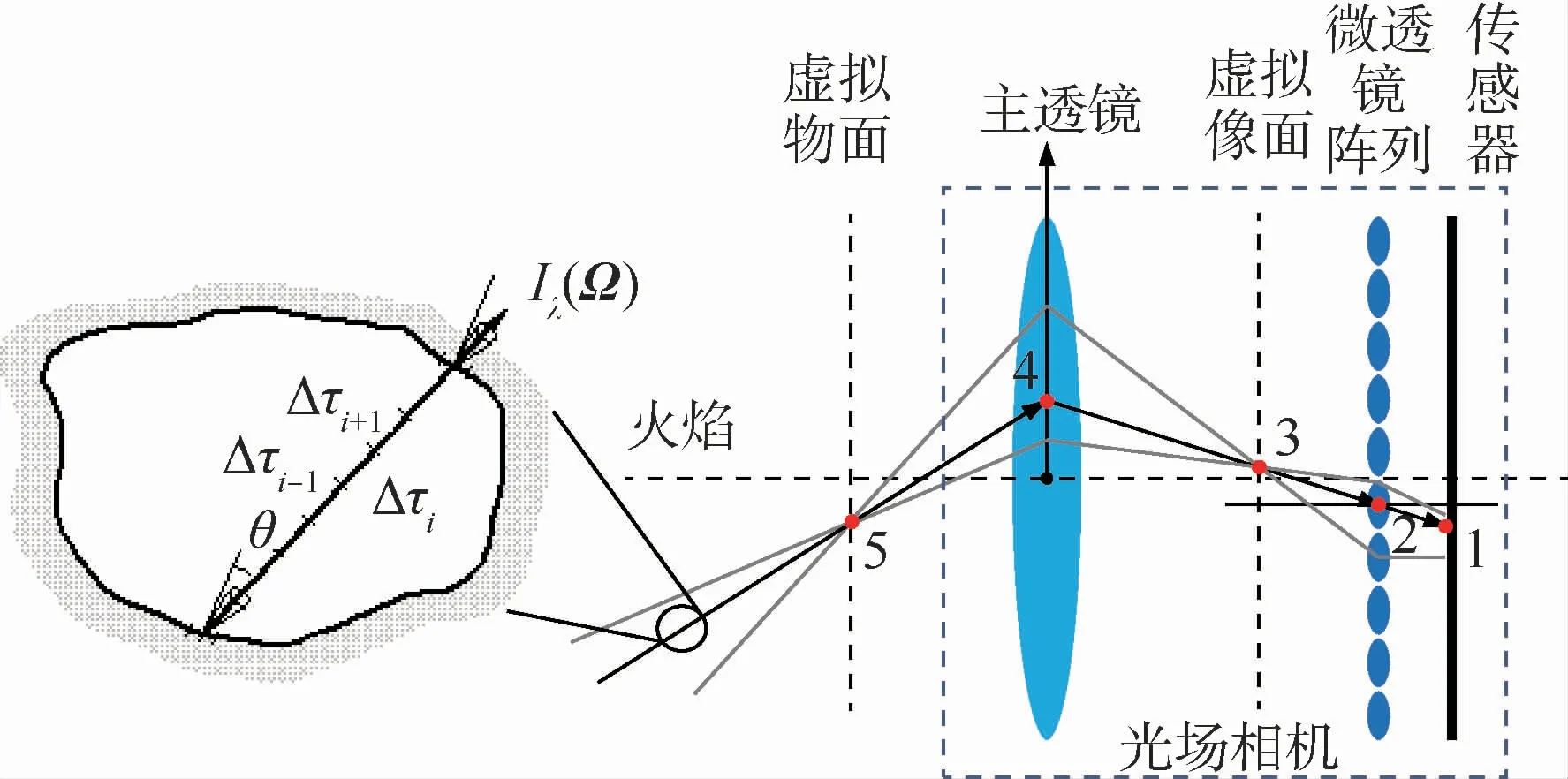
圖1 光場成像的射線追蹤示意圖Fig.1 Schematic diagram of ray tracing of light-field imaging

根據式（1）和式（2）所示的透鏡成像公式，可從像素點開始對采樣光線進行追蹤。

式中：sv為透鏡的物距，s為透鏡的像距，F為透鏡的焦距。對于主透鏡來說，sv為主透鏡與虛擬物面之間的距離，s為主透鏡與虛擬像面之間的距離，xv為光源點的坐標，x為對應的虛擬像點的坐標，F為主透鏡的焦距；對于微透鏡來說，sv為微透鏡陣列與虛擬像面之間的距離，s為微透鏡陣列與探測面之間的距離，xv為虛擬像點的坐標，x為與之對應的像素點的坐標，F為微透鏡的焦距。因此，當光場相機的結構參數已知時，可以根據式（1）和式（2）計算得到光線的位置信息，即光線經過各個平面的坐標。

在獲得各點的坐標后，可以根據各點的連線得到光線的方向信息。對于圖1所示的采樣光線，其在火焰內的傳輸方向可以根據點4和點5的連線得到。

式中：θ和φ分別為天頂角和圓周角。

基于上述光場成像模型，可以從光場相機拍攝到的光場圖像中獲得火焰邊界上的出射輻射強度的位置、方向和強度信息，為基于光場成像的火焰溫度場重建提供測量信號。

1.2 火焰輻射傳輸模型及算法

在通過光場圖像獲得火焰出射輻射強度信號之后，還需要建立出射輻射強度與火焰內部輻射強度之間的聯系，才能實現火焰內三維溫度場重建。火焰是一種典型的參與性介質，邊界上的出射輻射強度是其內部各點輻射強度的累積。火焰內的輻射傳輸過程可以用如下輻射傳輸方程來描述：

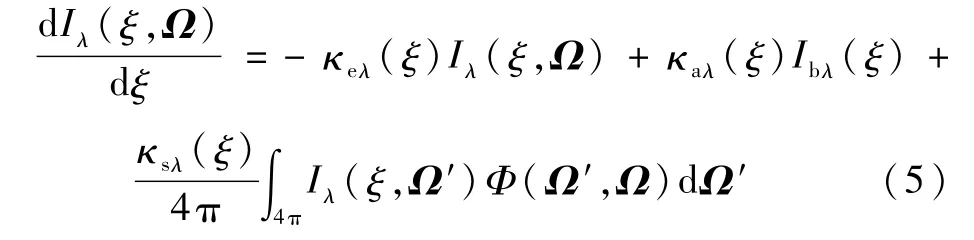
式中：Iλ（ξ，Ω）為介質在ξ位置處Ω 方向上的光譜輻射強度，W／（m2·μm·sr）；Ibλ（ξ）為介質在ξ位置處的自身黑體光譜輻射強度，W／（m2·μm·sr）；κeλ（ξ）為衰減系數，m-1；κaλ（ξ）為吸收系數，m-1；κsλ（ξ）為散射系數，m-1；Φ（Ω′，Ω）為Ω′方向入射并向Ω 方向散射的散射相函數。等號右側第二項和第三項均可以使輻射強度增強，因此將二者之和定義為廣義源項Sλ（ξ，Ω），即

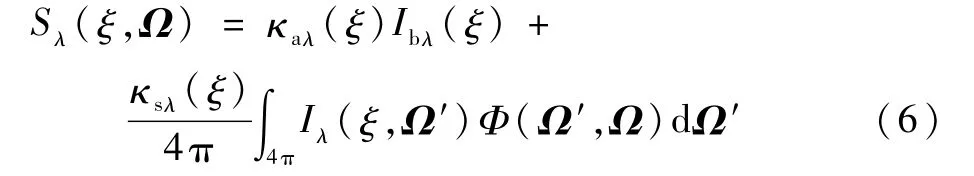
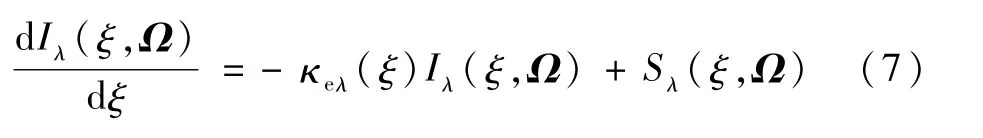
此時式（5）可以簡化為可以看出，若源項已知，則可將式（5）所示的積分微分方程簡化為式（7）所示的純微分方程，進而可以通過沿程積分求解出火焰某一方向上的出射輻射強度。廣義源項多流法就是在這種求解思路的基礎上建立的。強度求解的關鍵在于對廣義源項的求解。本文利用有限體積法（Finite Volume Method，FVM）計算火焰的廣義源項。首先采用FVM求解較少離散方向上的輻射強度，從而根據式（6）獲得火焰內的廣義源項分布，根據廣義源項的不變性［19］，增加了離散角度之后廣義源項的數值不發生改變，因此可以利用計算得到的廣義源項計算出更多離散方向上的輻射強度。如圖1所示，將Ω方向上探測線經過的火焰區域離散為N個網格，對式（7）在微元控制體內積分，可以得到

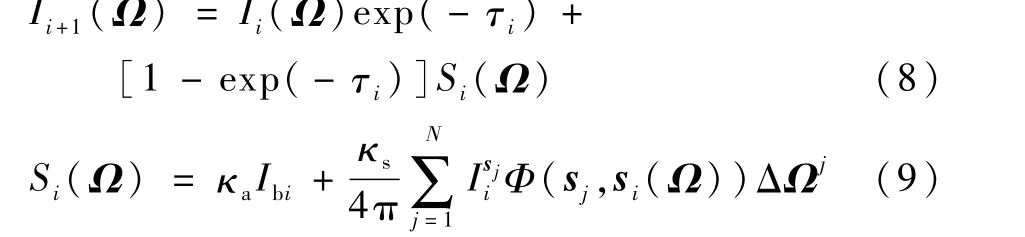
式中：κa為介質吸收系數，m-1；κs為介質散射系數，m-1；Ibi為控制體i自身黑體輻射強度，W／（m2·μm·sr）；τi為探測線穿過網格的光學厚度；為控制體i在離散方向sj上的輻射強度值；ΔΩj為控制立體角；Ii＋1（Ω）為穿過第i個網格后的輻射強度。因為火焰溫度遠高于周圍環境溫度，所以忽略環境輻射影響。假設每個網格內溫度均勻分布，則Ω方向上的火焰邊界出射輻射強度可由積分得到，其離散形式可表示為

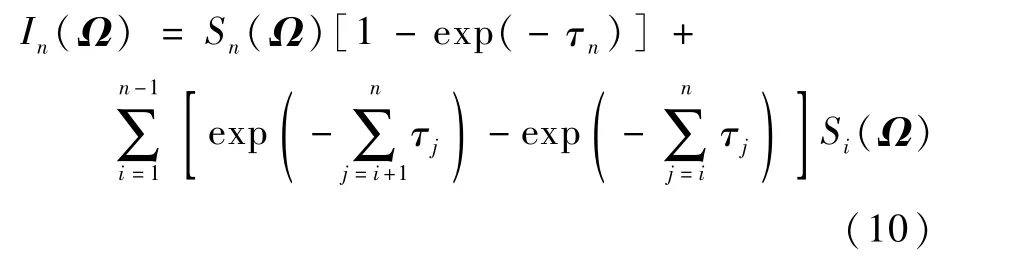
沿不同的探測方向對火焰內的輻射傳輸過程進行積分，可以得到火焰邊界上的出射輻射強度分布，將其寫成矩陣形式可表示為

式中：Aλ為衰減系數矩陣；Sλ為廣義源項向量；Iλ為出射輻射強度向量，即光場相機最終接收到的輻射強度分布。

2 溫度場重建算法

基于光場成像的火焰溫度場重建，即根據由光場相機拍攝到的火焰光場圖像獲得火焰邊界上的出射輻射強度分布，進而利用該出射輻射強度分布由火焰內的輻射傳輸模型重建出火焰的三維溫度場。當輻射特性參數已知時，式（11）中的未知數僅為廣義源項Sλ，可以將其視為線性方程組，通過求解式（11），可得到火焰內的源項分布。由式（6），火焰的自身黑體輻射強度包含在廣義源項中，當源項已知時，利用FVM 可以計算出火焰內各點的輻射強度，進而計算出火焰的自身黑體輻射強度項，根據普朗克定律，待重建的溫度場可以由火焰的自身黑體光譜輻射強度Ibλ計算得到，據此可實現火焰三維溫度場的重建。

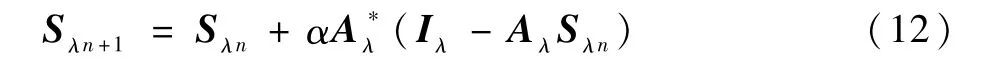
對于式（11），考慮到其系數矩陣Aλ是一個大型的稀疏矩陣，且問題本身具有非適定性，本文利用Landweber算法來求解方程組。對于式（11）所示的方程組，Landweber算法的求解格式如下：式中：α為松弛因子；A*為A的轉置矩陣。Landweber算法適用于求解大規模不適定問題，方法較為穩定，即使在測量值存在噪聲的情況下利用該算法也可以得到合理的解。但是傳統的Landweber算法迭代序列收斂速度很慢，為了加速收斂，本文采用了一種改進的迭代格式［20］：

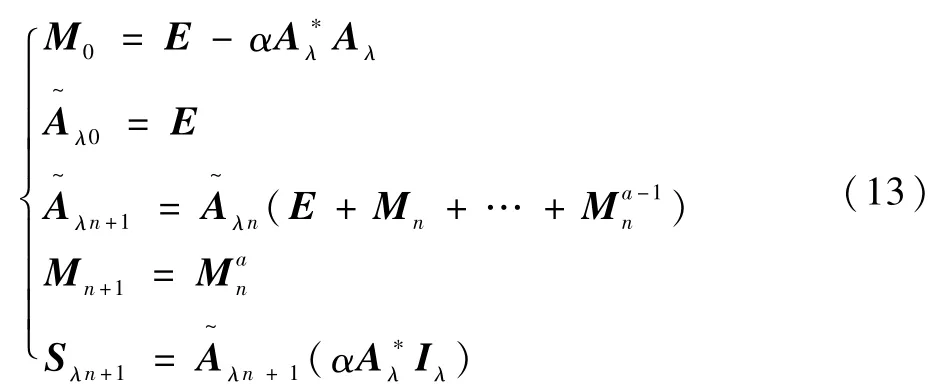
式中：a≥2為給定的正整數；E為單位矩陣；M 為過渡矩陣；n為迭代步數。雖然式（13）迭代一步的計算量要大于式（12），但是計算過程中總的迭代步數會大大減少。式（13）迭代k步，相當于式（12）迭代ak步，因此該迭代格式會大大提高算法的效率。在本文中取a＝4。

基于光場成像與Landweber算法的火焰溫度場重建流程如圖2所示。

此外，為了衡量Landweber算法性能的優劣，本文還利用LSQR算法重建火焰的三維溫度場以作為比較。該方法已被廣泛應用于基于輻射成像的火焰溫度場重建問題中，并被證明具有很高的重建精度。基于LSQR算法的火焰溫度場重建流程與基于Landweber算法相似，在此不做贅述。

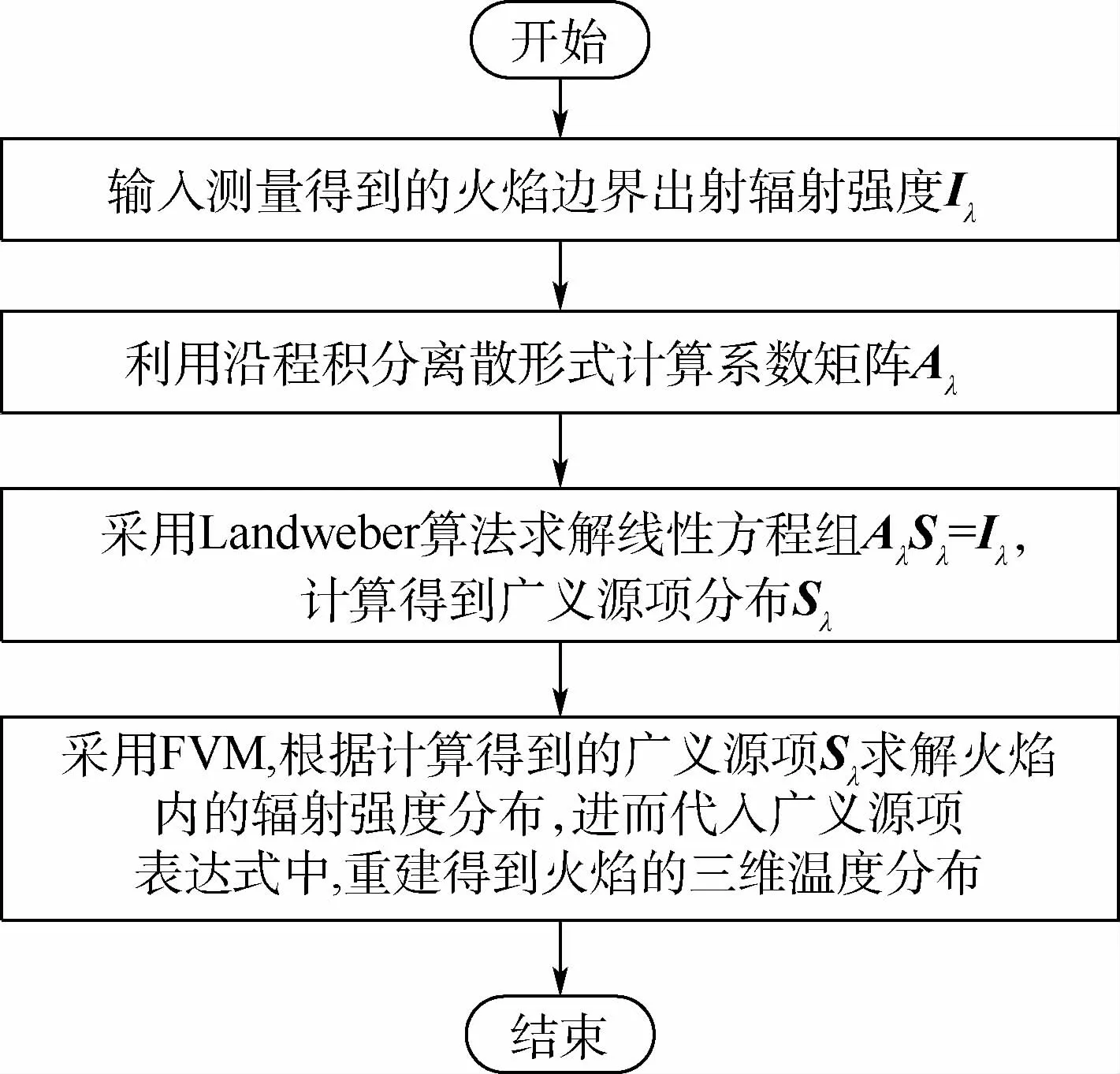
圖2 基于光場成像與Landweber算法的火焰溫度場重建流程Fig.2 Flowchart of flame temperature field reconstruction based on light-field imaging and Landweber algorithm

3 數值模擬結果與分析

在第1節成像理論模型的基礎上，開展數值模擬計算來檢驗算法的性能。考慮一圓柱型介質，介質半徑為0.05 m，高度為0.4 m，假設溫度分布為軸對稱分布。

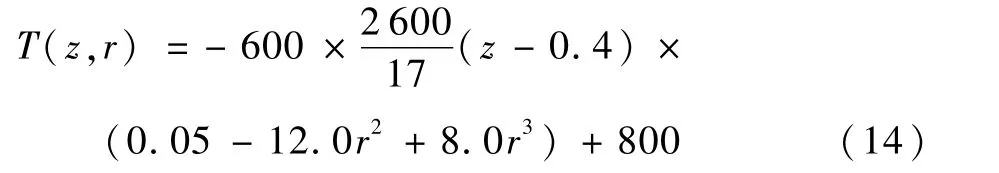
式中：z和r分別為軸向和徑向坐標。假設火焰的吸收系數為3m-1，散射系數為3m-1。在圓周角、半徑和軸向高度方向上將重建區域劃分為Nφ×NR×NL＝1×20×20個網格。

為了使模擬的輻射強度信號更貼合實際情況，在模擬的強度信號基礎上添加隨機測量噪聲，如下：

式中：為一個滿足標準正態分布的隨機數；σ為添加噪聲的標準差；Imea和Iexa分別為強度信號的測量值和精確值；γ為測量誤差。

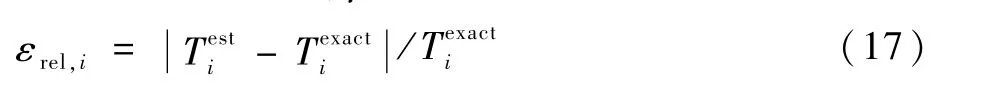
式中：εrel，i為單元網格溫度重建值與真值的相對誤差；為單元網格重建值；為單元網格的真實溫度值。溫度重建結果的平均相對誤差為

利用上述光場成像模型模擬構建了介質邊界輻射強度分布的光場圖像，如圖3所示。模擬研究中采用的光場相機結構參數見文獻［21］。

圖3 模擬光場圖像Fig.3 Simulated light-field image

分別利用Landweber算法，LSQR算法對火焰溫度場進行重建。為了研究測量誤差對重建精度的影響，分別添加了1%、3%、5%的測量誤差γ。不同測量誤差情況下2種算法的重建結果如圖4和圖5所示（圖中：R為半徑，Z為高度），縱截面上的重建相對誤差分布如圖6和圖7所示，平均重建相對誤差及計算時間對比如表1所示。

從圖4和圖5中可以看出，在添加測量誤差很小（小于3%）的情況下，采用2種算法重建出的溫度分布均十分接近于假定的溫度場分布；當測量誤差逐漸增大時，重建結果中出現了抖動，溫度場輪廓逐漸變得不規則，尤其是在添加了5%測量誤差的情況下，在介質頂部位置有了較明顯的波動。但從整體上看，重建的溫度分布仍然清晰可見，且與真值相近，因而結果仍然是合理的。

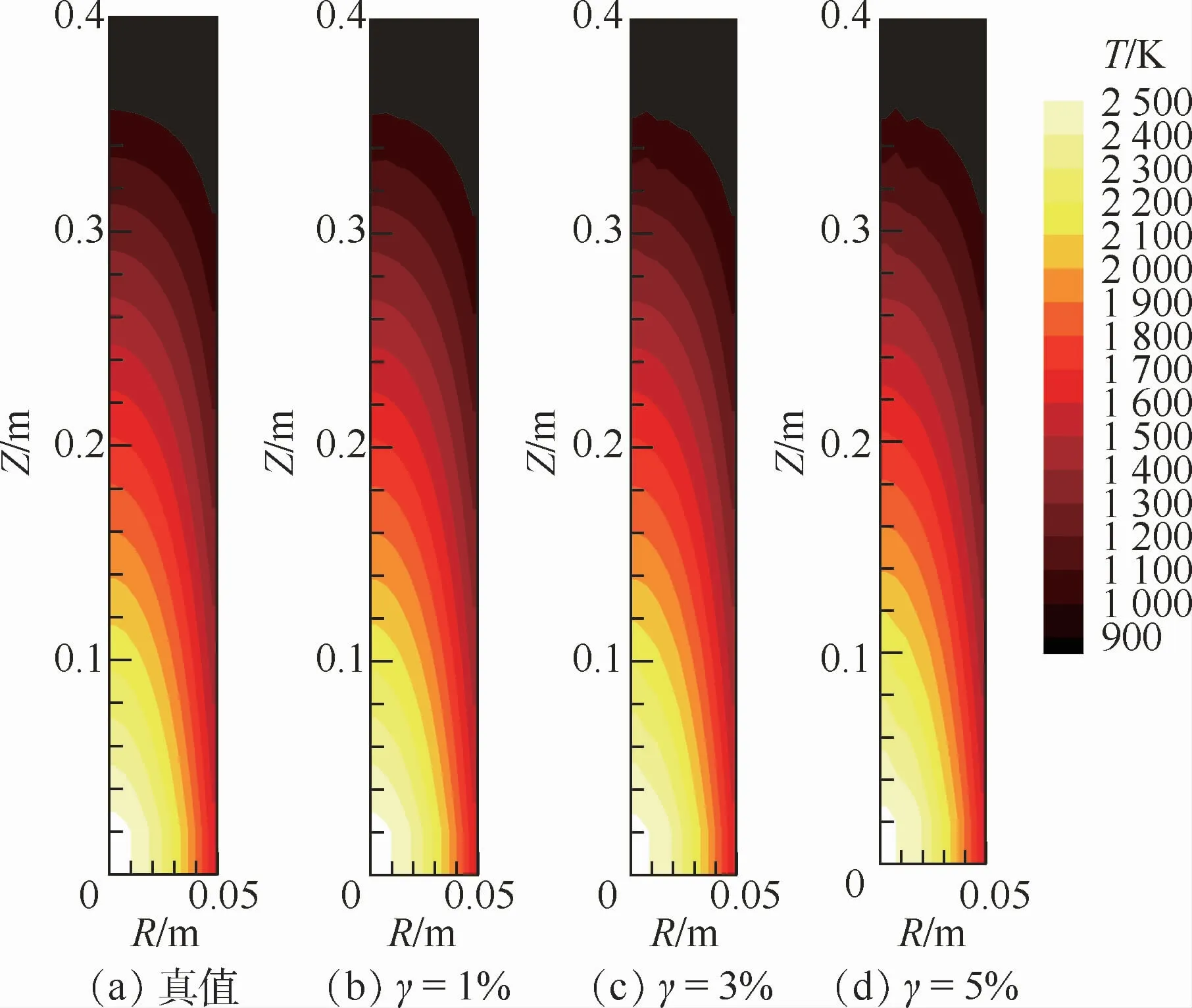
圖4 LSQR算法三維溫度場重建結果Fig.4 Reconstructed 3D temperature field distribution using LSQR algorithm

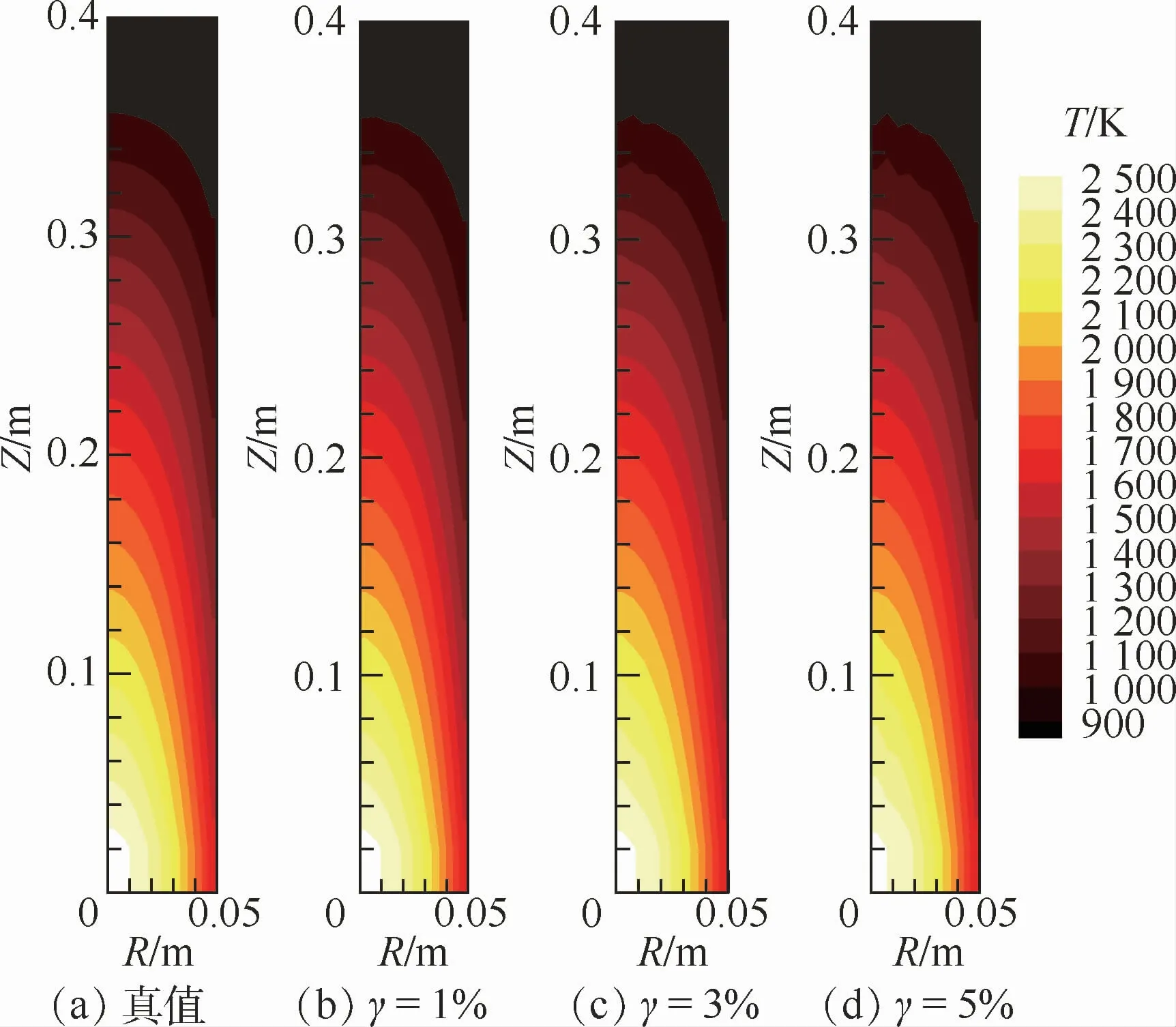
圖5 Landweber算法三維溫度場重建結果Fig.5 Reconstructed 3D temperature field distribution using Landweber algorithm

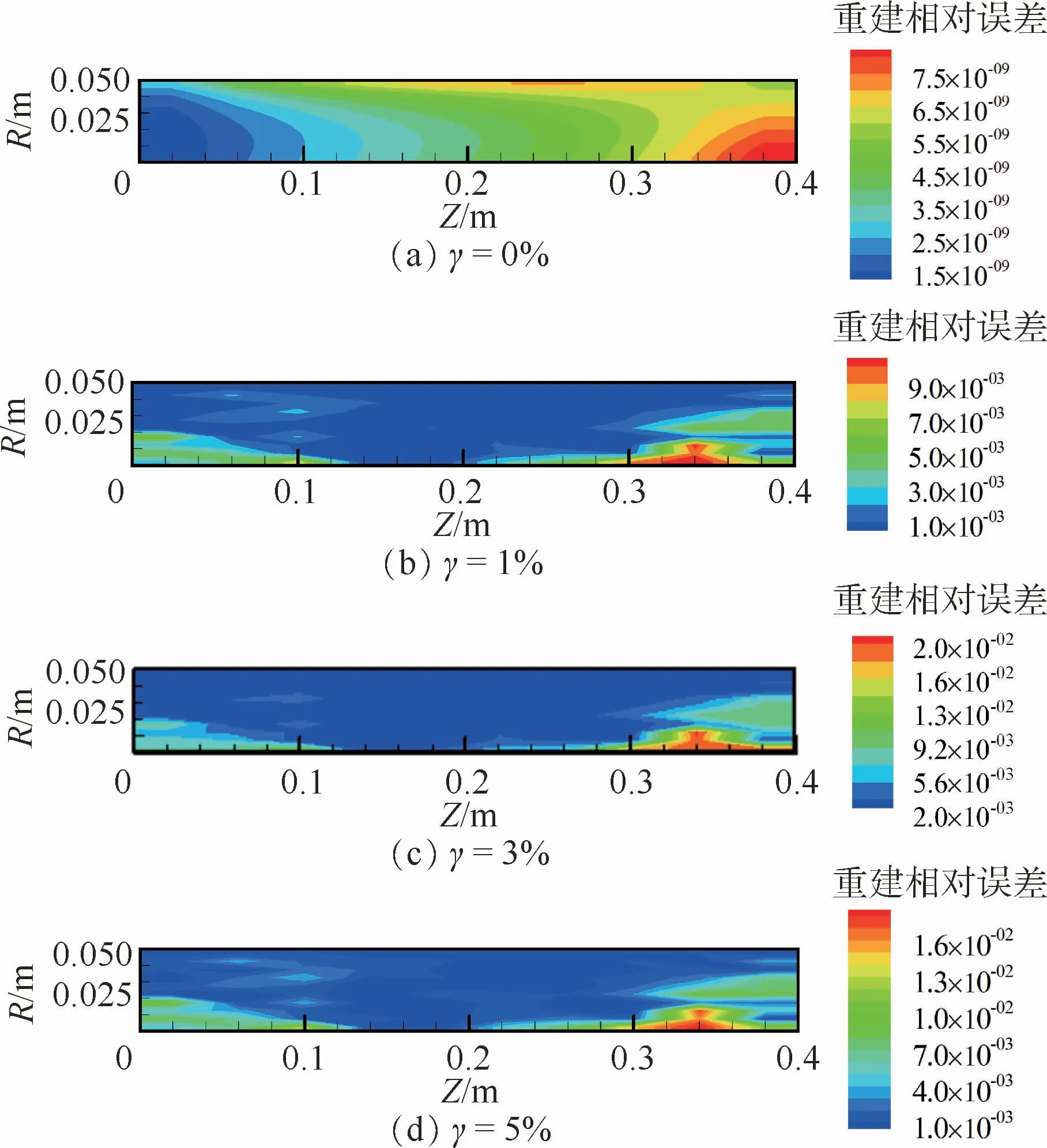
圖6 LSQR算法重建相對誤差分布Fig.6 Reconstruction relative error distribution of LSQR algorithm

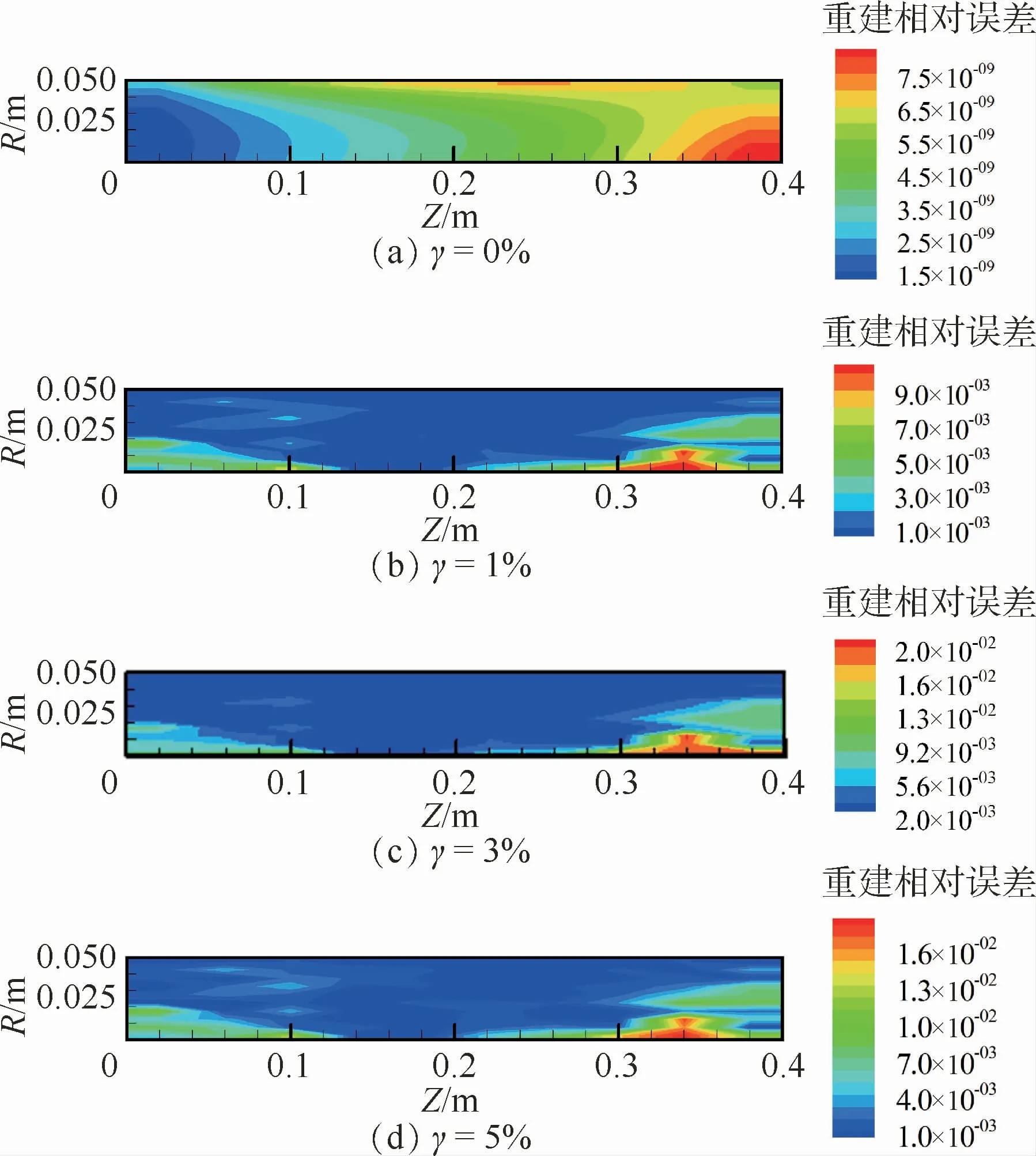
圖7 Landweber算法重建相對誤差分布Fig.7 Reconstruction relative error distribution of Landweber algorithm

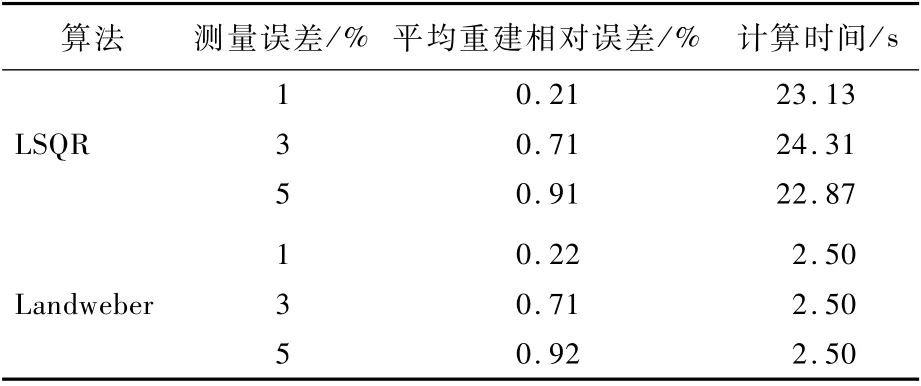
表1 LSQR算法與Landweber算法計算結果對比Tab le 1 Com parison of calcu lation resu lts between LSQR algorithm and Landweber algorithm

進一步從定量的角度分析重建結果的優劣。從重建相對誤差中可以看出，無論有無測量誤差，利用2種算法都可以得到比較合理的溫度場重建結果。在沒有測量誤差時，2種算法溫度場的重建結果精度很高，平均重建相對誤差均在10-9量級；隨著測量誤差的增大，重建相對誤差也隨之增大；但即使在添加5%的測量誤差的條件下，其溫度場重建相對誤差平均值也分別只有0.91%和0.92%。因此可以看出，2種算法都具有很高的計算精度，且計算結果精度相當。

從圖6和圖7中可以看出，火焰溫度場重建相對誤差較大的區域主要發生在火焰徑向中心處的軸向兩端位置，尤其是頂端區域誤差很明顯。對于溫度場軸對稱分布的火焰，由于內部強度的沿程衰減作用，其中心位置的網格單元的自身輻射信號到達相機過程中衰減得最嚴重，從而導致信息的缺失；并且由于探測線的分布導致穿過軸向兩端位置的單元的探測線數量少，從而測量數據中攜帶軸向兩端位置單元的信息相對較少。此外，結合圖4和圖5所示的溫度場真值及圖3所示的光場圖像可以看出，頂端位置處的介質單元溫度較低，其本身測量信號強度較弱，在添加了測量噪聲之后，測量信號更容易受到噪聲的干擾而失真，因此在這些位置的介質單元的溫度場重建相對誤差較大。

計算效率是衡量算法優劣的另一個重要指標。本文比較了2種算法在重建溫度場時所消耗的時間，如表1所示。可以看出，基于Landweber算法重建溫度場所需時間均短于LSQR算法所需時間。當2種算法達到相同的計算精度時，利用LSQR算法需要24 s左右的計算時間，而利用Landweber算法僅需要2.5 s，計算效率差距明顯。這主要是由于改進的迭代格式使得Landweber算法的迭代步數大大減少，從而縮短了計算時間。事實上，對于本算例，在存在測量誤差的情況下，Landweber算法僅計算了10步，而LSQR算法計算了5 000步，要遠多于Landweber算法。因此，在計算效率方面Landweber算法更勝一籌。綜合考慮計算效率與計算精度，Landweber算法更適用于基于光場成像的吸收散射性火焰三維溫度場重建問題。

4 結 論

1）本文提出了基于光場成像技術的吸收散射性火焰三維溫度場重建算法，構建了光場成像模型，采用廣義源項多流法作為正問題計算方法，將Landweber算法引入到火焰三維溫度場重建問題中，利用Landweber算法計算廣義源項分布進而重建出火焰的三維溫度分布。同時引入LSQR算法作為對比，以衡量Landweber算法的性能。

2）在理論模型的基礎上開展數值模擬研究，計算結果表明無論有無測量誤差，利用2種算法均可以很好地重建出介質的三維溫度場。隨著測量誤差的增大，2種算法的重建相對誤差均有增大，但使在添加5%的測量誤差的條件下，溫度場平均重建相對誤差也分別只有0.91%和0.92%，仍在可接受范圍內。

3）對比結果表明，2種算法具有相當的計算精度，但Landweber算法的計算效率要明顯優于LSQR算法，在相同重建精度條件下，Landweber算法的計算時間為2.5 s，而LSQR算法需要24 s，因而Landweber算法要更適用于火焰三維溫度場重建問題。結果表明，提出的基于光場成像與Landweber算法的吸收散射性火焰溫度場重建方法是可行的，在輻射成像測溫領域具有很廣闊的應用前景。