帶擴展流的矩形級聯
豆丹丹,叢藝坤
(核工業理化工程研究院 粒子輸運與富集技術重點實驗室,天津 300180)
高豐度的中間組分穩定同位素廣泛應用于醫藥、工農業生產、基礎物理研究等領域,但即使通過現在較為成熟的同位素分離技術,高豐度的中間組分同位素也非常難獲取。這主要是由于相對邊緣組分來說,中間組分在級聯的某端濃縮時不可避免會有其他同位素被濃縮,因此中間組分濃縮的豐度會有一個限值[1]。對于多組分分離,為提高中間組分同位素的豐度,通常有兩種方法。一種是多遍分離,將第一遍的精料(或貧料)作為第二遍供料,而后在貧料(或精料)端取料,這樣可以在分離過程中將中間組分變為邊緣組分,從而提高產品的豐度。該方法可獲取任意高豐度的中間組分,在實際中應用最廣。但需要多遍分離,增加了機器數與分離時間,提高了分離成本。第二種方法為中間取料,由于相對分子質量處在中間位置的同位素的豐度通常在級聯的中間某級取得最大值[2],如果能夠在中間組分豐度達到峰值的地方取料,則能夠在不改變級聯規模和生產成本的前提下,得到中間組分豐度較高的產品。該方法適用于獲取需求量小,豐度較高的同位素產品。
研究表明,即使應用中間取料,中間組分同位素的豐度依然存在限值。利用中間取料的方法獲取更高豐度的中間組分,需提高中間組分在中間級的豐度。文獻[3-5]從理論上證實了帶擴展流的Q級聯可提高中間組分在中間級的豐度,由于Q級聯為理論理想模型,而實際分離穩定同位素常用的級聯模型是矩形級聯,因此將帶擴展流的Q模型級聯思想應用到實際中以提高中間取料的豐度,即為帶擴展流的矩形級聯。Smirnov[6]推導了擴展流在精料段的矩形級聯計算方程,且以183WF6為例,證實了此類級聯提高中間取料豐度的可行性。但在多組分同位素分離中,有些較重組分應在貧料端濃縮,因此擴展流應在貧料段。本文在此基礎上設計適用于較重中間組分同位素分離的級聯模型,即帶擴展流的矩形級聯(擴展流在貧料段),并推導該級聯模型有附加取料流的計算方程,通過謝全新等[7-9]提出的快速穩定收斂的穩態計算方程進行求解。并以184WF6為例證實該級聯模型適用于分離較重的中間組分同位素,提高中間取料獲得產品的豐度,為實際級聯設計與同位素生產提供理論支持。
1 級聯模型及級聯方程
本文研究的帶擴展流的矩形級聯模型示于圖 1。級聯是雙管道的逆流型矩形級聯,即將第s+1級的貧化流L″(s+1)送回到第s級,與s-1級的濃縮流L′(s-1)混合,作為第s級的供料L(s)。第s級供料流、貧化流和濃縮流中的組分豐度分別用Ci(s),C″i(s)和C′i(s)表示,其中i=1,…,m(m是同位素混合物的組分數)。級聯具有四股外部流,即供料流F、精料流P、貧料流W、附加取料流E,他們的組分豐度分別為CiF、CiP、CiW、CiE。N表示級聯的總級數,f為供料級,l表示附加取料流的位置,s0為級聯擴展流的邊界級。

圖1 帶擴展流的矩形級聯模型
在多組分同位素級聯理論中,通常定義第i組分對第j組分的相對全分離系數qij為:
(1)
通常情況下,相對分離系數隨級的供料組分豐度Ci以及級的分流比θ的變化而變化,但對于大部分基于分子動力學的分離方法,相對全分離系數基本上不隨上述參量變化,并可表示為:
(2)
式中:q0為基本全分離系數;Mj,Mi為第j,i兩種組分的摩爾質量。
(3)
(4)
在帶擴展流的矩形級聯中,其流量由下式定義:
(5)
其中K為擴展級流量與常規級流量比例系數,L為常規級流量。
假設級聯各級的相對全分離系數保持不變,當級聯穩態運行時,第s級到精、貧取料級的質量守恒方程以及組分質量守恒方程可以分別表示為[10]:
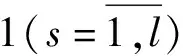
L′(s)-L″(s+1)=-W
(6)
L′(s)C′i(s)-L″(s+1)C″i(s+1)=-WCiW
(7)
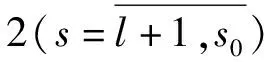
L′(s)-L″(s+1)=-E-W
(8)
L′(s)C′i(s)-L″(s+1)C″i(s+1)=
-ECiE-WCiW
(9)
其中L(s)=KL
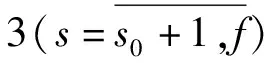
L′(s)-L″(s+1)=-E-W
(10)
L′(s)C′i(s)-L″(s+1)C″i(s+1)=
-ECiE-WCiW
(11)

L′(s)-L″(s+1)=P
(12)
L′(s)C′i(s)-L″(s+1)C″i(s+1)=PCiP
(13)
其中L(s)=L
整個級聯的物質守恒方程為:
F=P+W+E
(14)
FCiF=PCiP+WCiW+ECiE
(15)
考慮到L′(s)=θsL,L″(s)=(1-θs)L,利用關系式(3)~(5)以及各級組分守恒方程Ci=θsC′i+(1-θs)C″i,方程(6)~(13)可以轉換成如下形式:
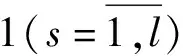
(16)
(17)
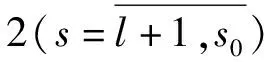
(18)
(19)
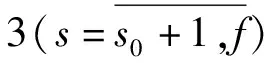
(20)
(21)
其中
(22)
(23)

(24)
(25)
其中
(26)
守恒方程可改寫為:
(27)
(28)
為求解方程組(16)~(28)應補充邊界條件
(29)
如圖1所示在級聯第②部分和第③部分之間存在一個流量跳躍點s0。實際中,一般在兩個階梯之間引入回流,構成引入回流的階梯級聯。第②部分和第③部分具體的連接情況示于圖2,其中λ為回流量占原流量的比例。
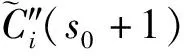
(30)
參數λ是根據實際需求計算得到的,如在文獻中,λ參數的設定是為了使得前后分流比θ連續,因此λ具體表達式為:
(31)
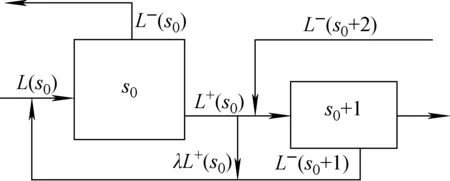
圖2 帶擴展流矩形級聯兩部分間的連接方式
2 級聯穩態方程組求解
如果給定供料組分豐度CiF、相對供料流量F/L、相對精料流量P/L(或相對貧料流量W/L)、相對附加流量E/L、級聯總級數N、供料級f、流量變化級s0、附加取料級l以及基本全分離系數q0和擴展倍數K,通過求解方程組(16)~(31)可以確定帶附加取料流擴展矩形級聯的精料組分豐度CiP、貧料組分豐度CiW,級聯各級供料流、濃縮流和貧化流中的組分豐度Ci(s)、C′i(s)和C″i(s)以及級聯各級分流比θs。
為求解方程組(16)~(26)利用準線性化方法[7-9],通過前一次的迭代值計算級聯方程組中的非線性因子從而使其準線性化,方程中的非線性項可表示為:
s=1,…,f-1
(32)
s=f,…,N
(33)
γ為當前迭代次數。
3 帶擴展流矩形級聯的優越性
以分離WF6同位素為例,目標組分為184WF6,利用上述帶擴展流的矩形級聯進行分離。高豐度的184WF6吸收截面小,可作為空間堆發電元件中發電極的涂層,WF6的天然豐度列于表 1。由于184WF6屬于較重組分,應從貧料端取料。

表1 WF6的天然豐度
同時,選取流量相同的常規矩形級聯作為比較,級聯長度、供料位置由Q級聯優化決定,附加取料流固定為E/W=0.06,其他具體參量列于表 2。
圖3顯示的為帶擴展流的矩形級聯和常規矩形級聯的流量部分,保持這兩個級聯模型的總流量相等。
184WF6分別在流量相同的帶擴展流矩形級聯和常規矩形級聯下的豐度分布示于圖4。帶擴展流的矩形級聯附加取料流處的豐度為81.23%,而常規矩形級聯附加取料流處的豐度為78.52%,因此在相同的流量下,帶擴展流的矩形級聯可從中間級取得更高豐度的中間組分。從圖中可以看出,184WF6在帶擴展流的矩形級聯中的豐度分布峰值更加高陡,而在常規矩形級聯中分布較為平緩,因此帶擴展流相當于將“尖峰”更加聚集,可獲取的豐度更高。而且在精料段,184WF6在帶擴展流的矩形級聯的豐度一直低于在常規矩形級聯中的豐度,帶擴展流的矩形級聯可將中間組分分離更加徹底。因此,在相同的總流量下,取得相同量的產品,帶擴展流的矩形級聯可比常規矩形級聯獲取更高豐度的中間組分。

表2 帶擴展流的矩形級聯和常規矩形級聯的計算參量

圖3 帶擴展流的矩形級聯(實線2)和常規矩形級聯(虛線1)的流量分布
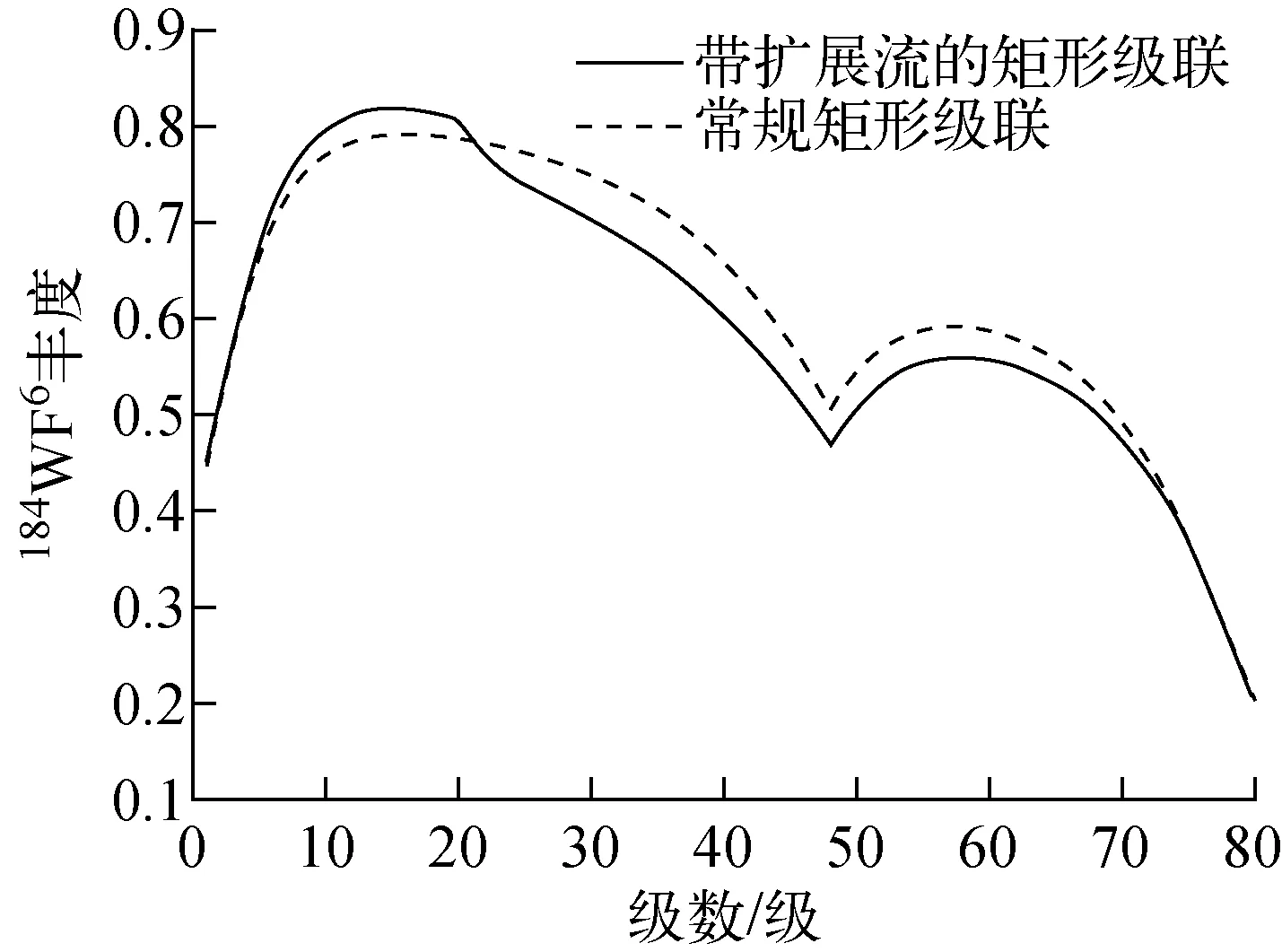
圖4 184WF6的豐度分布
特別值得注意的是,雖然W-184在帶擴展流的矩形級聯的附加流中豐度比常規矩形級聯高,但在貧料端,W-184的豐度在兩種級聯中幾乎相同,其中在帶擴展流的矩形級聯中為41.02%,在常規的矩形級聯為41.31%,而且此時貧料端流量相同。也就是,即使在帶擴展流的矩形級聯中間級取料高豐度的中間組分,取料端同時取相同量的產品時,不會降低該組分在取料端的豐度。帶擴展流的矩形級聯有能力在級聯兩端獲取與常規矩形級聯相同量相同豐度產品的同時,還可在中間級獲取比常規矩形級聯更高豐度的產品。
其他組分在兩種級聯中的豐度分布示于圖5。從5圖中結果可以看出,在擴展流部分,輕組分如W-180、W-182、W-183在帶擴展流的矩形級聯中豐度比在常規矩形級聯的豐度高,而重組分如W-186在前者中的豐度比在后者的豐度低。在擴展流的跳躍點s0,濃縮流有一部分又返回到原來級,使得s0輕組分的豐度比之前要高,整體造成1~s0的輕組分豐度提高,重組分豐度降低。
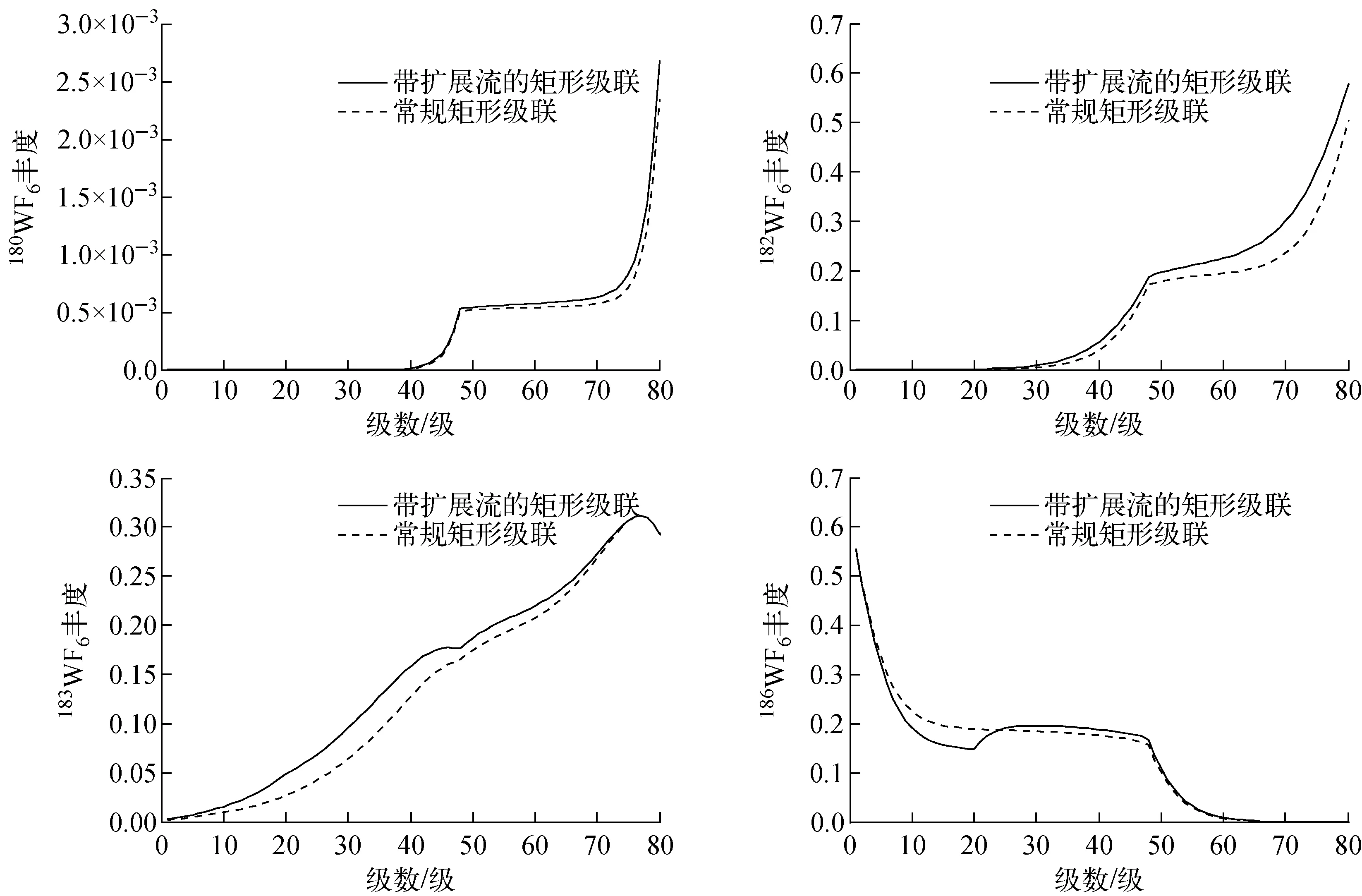
圖5 WF6其他組分在兩種級聯的豐度分布
從以上可以看出,正如Q級聯一樣,帶擴展流的矩形級聯改變了同位素各個組分在級聯中的豐度,可以在中間級獲取到更高豐度的中間組分。
4 結論
建立了適用于多組分同位素中間組分分離的帶附加流的擴展型矩形級聯數學模型,得到描述該數學模型的穩態級聯方程組,用快速穩定的穩態計算方法求解了級聯方程組。證實了帶擴展流的矩形級聯在相同的總流量下,可以在中間級獲取比常規矩形級聯更高豐度的較重中間組分,為實際生產較重組分的中間組分的級聯建設提供了理論支持。
在實例分離184WF6中,在相同的總流量下,帶擴展流的矩形級聯中間級的豐度較常規矩形級聯提高了約3%。且值得注意的是,在產品端兩種級聯的豐度沒有差別。因此帶擴展流的矩形級聯有能力在級聯兩端獲取與常規矩形級聯相同量相同豐度產品的同時,還可在中間級獲取比常規矩形級聯更高豐度的產品。

